Average Consensus in Networks of Multi-Agent with Multiple Time-Varying Delays ()
The average consensus in undirected networks of multi-agent with both fixed and switching topology coupling multiple time-varying delays is studied. By using orthogonal transformation techniques, the original system can be turned into a reduced dimensional system and then LMI-based method can be applied conveniently. Convergence analysis is conducted by constructing Lyapunov-Krasovskii function. Sufficient conditions on average consensus problem with multiple time-varying delays in undirected networks are obtained via linear matrix inequality (LMI) techniques. In particular, the maximal admissible upper bound of time-varying delays can be easily obtained by solving several simple and feasible LMIs. Finally, simulation examples are given to demonstrate the effectiveness of the theoretical results.
1. Introduction
Recently, more and more researchers have paid a great deal of attention on distributed coordinated control of networks of dynamic agents within the control community. Especially the consensus problem was discussed widely, which can be attributed to the broad applications of multi-agent systems in many areas, including cooperative control of unmanned air vehicles, formation control of multi-robot, flocking, swarming, distribution sensor fusion, attitude alignment and congestion control in communication networks, etc. In cooperative control of multi-agent system, a critical issue is to design appropriate protocol and algorithms such that all agents can reach a common consensus value. This problem is called consensus problem.
In the past decades, some theoretical results have been established in [1–11], to name a few. In [1], Vicsek et al. proposed a simple model but interesting discrete-time model of autonomous agents all moving in the plane with the same speed but with different headings. Simulation results provided in [1] show that all agents can eventually move in the same direction without centralized coordination. The first paper providing a theoretical explanation for these observed behaviors in Vicsek model is [2]. The theoretical results in [2] are extended to the case of directed graph by Ren et al. [3], in which matrix analysis and algebraic graph theory were used. Moreau [4] used a set-valued Lyapunov approach to study consensus problem with unidirectional time-dependent communication links. Saber et al. [5] discussed average consensus problem. When network communication is affected by time delay, the consensus problem is investigated in [5–7]. In [8], Saber provided a theoretical framework for analysis of consensus algorithms for multi-agent networked systems with an emphasis on the role of directed information flow, robustness to changes in network topology due to link/node failures, time-delays, and performance guarantees. Ren et al. provided a tutorial overview of information consensus in multivehicle cooperative control in [9]. Yu et al. [10] proposed weighted average consensus in direction networks and unidirectional networks with time-delay. Multi-vehicle consensus with time-varying reference state was discussed in [11]. Some other issues on consensus problem can be found in [12–16].
Currently, consensus problem for multi-agent networks with time delay was studied using linear matrix inequality method, for example [17–19] and [20]. In time delay systems of multi-agent, the network topology of multi-agent is a key factor in the analysis of stability of multi-agent system. Average consensus problem for multi-agent networks with both constant and time-varying delay has been extensively considered for the cases of multi-agent undirected and/or direction networks with fixed and/or switching topology [17,18] and [19]. However, the studies on consensus problem of multi-agent networks with multiple timevarying delays are still sparse. In this case, theoretical analysis is more challenging. In [20], the authors proposed a consensus protocol for multi-agent undirected network with multiple time-varying delays based on LMI method.
In this paper, we study the average consensus problem for continuous time undirected networks of multiagent, coupling multiple time-varying delays. Because the closed-loop system matrix is singular and traditional LMI-based control theory is invalid. Therefore, theoretical analysis for this case is a challenging task. By using orthogonal transformation techniques, sufficient conditions based on LMI for multi-agent achieving average consensus is obtained. Compared to [20], a different approach is used in this paper. First of all, the original system is turned into a reduced dimensional system by orthogonal transformation; Secondly, via constructing a different Lyapunov-Krasovskii function, a sufficient condition expressed as LMI is proposed to guarantee all agents reach average consensus in fixed and switching network. Finally, the maximal admissible upper bound of multiple time-varying delays can be easily obtained by solving several simple and feasible LMIs.
This paper is organized as follows. Section 2 is the notation and formally states the problem. Section 3 contains our main results. Simulation results are presented in Section 4. The concluding remarks are made in Section 5.
2. Problem Statement and Preliminaries
In this section, we provide a brief introduction about algebraic graph theory [24] and state the problem.
2.1. Algebraic Graph Theory
Let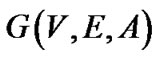 be a weighted undirected graph of order
be a weighted undirected graph of order , where
, where  is the set of nodes,
is the set of nodes,  is the set of edges, and
is the set of edges, and  is a weighted adjacency matrix. The node indexes belong to a finite index set
is a weighted adjacency matrix. The node indexes belong to a finite index set .
.
In undirected graph,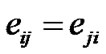 .
. 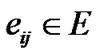 if and only if
if and only if . Moreover, we assume
. Moreover, we assume  for all
for all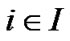 . A undirected graph is always connected. The set of neighbors of nodes
. A undirected graph is always connected. The set of neighbors of nodes  is denoted by
is denoted by
 .
.
The out-degree of node  is defined as follows:
is defined as follows: . The degree matrix of graph
. The degree matrix of graph 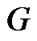 is a diagonal matrix
is a diagonal matrix , where
, where 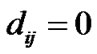 for all
for all  and
and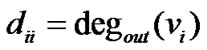 . The Laplacian matrix associated with the graph is defined as
. The Laplacian matrix associated with the graph is defined as

An important fact of  is that all the row sums of
is that all the row sums of  are zero and thus
are zero and thus 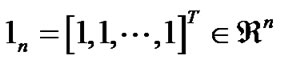 is an eigenvector of
is an eigenvector of  associated with the eigenvalue
associated with the eigenvalue .
.
Lemma 1 [5]. If the undirected graph 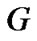 is connected, then its Laplacian matrix
is connected, then its Laplacian matrix  satisfies:
satisfies:
1)  is symmetric and rank
is symmetric and rank ;
;
2) zero is one eigenvalue of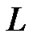 , and
, and  and
and  are the corresponding left and right eigenvector respectively, then,
are the corresponding left and right eigenvector respectively, then,  and
and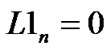 ;
;
3) the rest  eigenvalues are all positive and real.
eigenvalues are all positive and real.
2.2. Consensus Problem on Network
Consider a group of  agents with dynamics given by
agents with dynamics given by
 ,
, (1)
(1)
where  is the state of the
is the state of the  th agent at time
th agent at time , which might represent physical quantities such as attitude, position, temperature, voltage, and so on, and
, which might represent physical quantities such as attitude, position, temperature, voltage, and so on, and  is the control input (or protocol) at time
is the control input (or protocol) at time .
.
We say protocol  asymptotically solves the consensus problem, if and only if the states of agents satisfy
asymptotically solves the consensus problem, if and only if the states of agents satisfy , for all
, for all . Furthermore, if
. Furthermore, if We say protocol
We say protocol  asymptotically solves the average consensus problem.
asymptotically solves the average consensus problem.
2.3. Control Protocol for Time Delay
Let  notes the time delay for information communicated from agent
notes the time delay for information communicated from agent to agent
to agent . Because of time delay, two difficult consensus protocols have been studied. One is
. Because of time delay, two difficult consensus protocols have been studied. One is
 ,
, (2)
(2)
and the other is
 ,
, . (3)
. (3)
Literature [5] have taken the protocol in (2) with into account, and obtained that it can asymptotically solves the average consensus problem in the fixed and undirected network topology if and only if
into account, and obtained that it can asymptotically solves the average consensus problem in the fixed and undirected network topology if and only if . Some conclusions also were investigated in [16-18].
. Some conclusions also were investigated in [16-18].
For consensus protocol in (3), communication delay only affects the agents who are transmitted. Literature [4] has established the consensus results in the directed and dynamically switching graph. Some results also appeared in [21–23].
In this paper, we are interested in discussing the average consensus problem in network of dynamic agents with fixed and switching topology coupling multiple time-varying delays, where the information passes through different edge with different time-varying delays. To solve such a problem, we assume the time delay satisfies 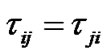 in undirected graph, i.e., the delays in transmission from
in undirected graph, i.e., the delays in transmission from  to
to 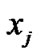 and
and  to
to  coincide. So we use the following protocol:
coincide. So we use the following protocol:
 ,
, (4)
(4)
With (4), (1) can be written in matrix form:
 , (5)
, (5)
where , and
, and 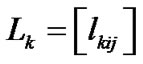 is the matrix defined by
is the matrix defined by

Because of is symmetric and
is symmetric and  in the undirected network, we can obtain
in the undirected network, we can obtain  is a symmetric and
is a symmetric and .
.
The time-varying delay ,
, is assumed to satisfy the follow inequations:
is assumed to satisfy the follow inequations:


 (6)
(6)
where  and
and  are constants.
are constants.  and
and  are the upper bound of
are the upper bound of  and
and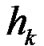 , namely,
, namely,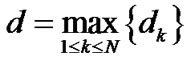 ,
, .
.
In the undirected network with switching topology, we address the follow hybrid system:
 ,
, . (7)
. (7)
where the map  is a switching signal that determines the network topology, and
is a switching signal that determines the network topology, and  denotes the total number of all possible switching undirected graphs.
denotes the total number of all possible switching undirected graphs.  is the Laplacian matrix of the graph
is the Laplacian matrix of the graph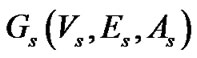 that belongs to a set
that belongs to a set , which is obviously finite.
, which is obviously finite.
Lemma 2 (Schur complement [25]). Let ,
,  ,
,  be given symmetric matrices such that
be given symmetric matrices such that , then
, then 
 .
.
Lemma 3. For any Laplacian matrix  of undirected connected network, there exists an orthogonal matrix
of undirected connected network, there exists an orthogonal matrix  such that
such that

where the last column of matrix  is
is 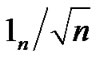 ,
,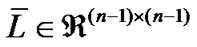 .
.
Proof: Because  and
and  are the corresponding left and right eigenvector respectively. The proof of this lemma is straightforward.
are the corresponding left and right eigenvector respectively. The proof of this lemma is straightforward.
3. Main Results
In this section, we provide the convergence analysis of the average consensus problem in undirected network with fixed and switching topology coupling multiple time-varying delays. Sufficient conditions expressed as LMI are presented for undirected networks of multiagent with fixed and switching topology, respectively.
3.1. Networks with Fixed Topology
If the fixed communication topology  is kept connected, we have
is kept connected, we have , and
, and , which imply
, which imply . Then,
. Then,  is an invariant quantity. Thus we have the decomposed equation
is an invariant quantity. Thus we have the decomposed equation , where
, where 
 , satisfies
, satisfies , i.e.,
, i.e., . Then (5) is equivalent to
. Then (5) is equivalent to
 . (8)
. (8)
By Lemma 3, we have
 then
then
 .
.
Let , where
, where . Then (8) can be transformed into the following equation:
. Then (8) can be transformed into the following equation:
 (9)
(9)
where satisfies
satisfies .
.
Lemma 4. If , then
, then .
.
Proof: From , we have
, we have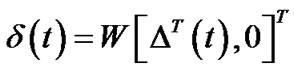 . Therefore, when
. Therefore, when , we have
, we have . This completes the proof.
. This completes the proof.
In the following section, we will discuss the convergence of dynamical system (9), that is .
.
Theorem 1. Consider an undirected network of multi-agent with fixed topology coupling multiple time-varying delays satisfies (6). Assume the communication topology  is kept connected. Then, system (5) asymptotically solves the average consensus problem, if there exist positive definite matrices
is kept connected. Then, system (5) asymptotically solves the average consensus problem, if there exist positive definite matrices 
 , satisfying
, satisfying
 (10)
(10)
where ,
,


Proof: Define a Lyapunov-Krasovskii function for system (9) as follows:
 ,
,
 ,
,
 ,
,

where ,
,  and
and are positive definite matrix. Along the trajectory of system (9), we have
are positive definite matrix. Along the trajectory of system (9), we have
 ,
,



 ,
,

 .
.
By Newton-Leibniz formula

and note that  hold for any appropriate positive definite matrix
hold for any appropriate positive definite matrix , we have:
, we have:
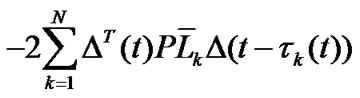

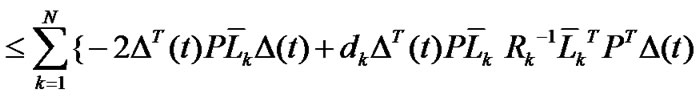

Consequently,





Then, a sufficient condition for 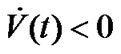 is
is
 (11)
(11)
and
 (12)
(12)
As a result, the matrix inequalities (11) hold, if and only if
 (13)
(13)
Then, by Schur complement formula the matrix inequality (13) is equivalent to
 (14)
(14)
where  is defined in (10).
is defined in (10).
Therefore, from Lemma 4, average consensus can be achieved if the matrix inequality (6) holds. This completes the proof.
3.2. Networks with Switching Topology
Considering the switching communication topology 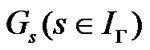 with system (7), we can obtain the following disagreement switching system:
with system (7), we can obtain the following disagreement switching system:
 , (15)
, (15)
where  satisfies
satisfies
 .
.
Theorem 2. Consider a undirected network of multi-agent with switching topology coupling multiple time-varying delays satisfies (6). Assume the communication topology  is kept connected. Then, system (7) asymptotically solves the average consensus problem, if there exist positive definite matrices
is kept connected. Then, system (7) asymptotically solves the average consensus problem, if there exist positive definite matrices , satisfying
, satisfying
 , (16)
, (16)
where ,
,


Proof: The proof of theorem 2 is similar to that of theorem 1, so it is omitted here.
Remark: When  of the condition (6) is replaced with
of the condition (6) is replaced with , we can obtain corresponding results if choosing
, we can obtain corresponding results if choosing .
.
4. Simulation
In this section, simulation examples will be given to validate the theoretical results obtained in the previous section. Consider a group of 10 agents labeled 1 through 10. Figure 1 shows four examples of undirected graph, which are all connected, and the corresponding adjacency matrices are limited to 0-1 matrices. Let the orthogonal matrix  is
is


where the last column of matrix  is
is . For simplicity, we assume
. For simplicity, we assume 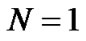 in undirected networks of multi-agent with both fixed and switching topology.
in undirected networks of multi-agent with both fixed and switching topology.
4.1. Examples of Networks with Fixed Topology
Consider an undirected network with fixed topology  in Figure 1. Employing Theorem 1, we have:
in Figure 1. Employing Theorem 1, we have:
1) for , i.e.,
, i.e.,  ,
, . Figure 2 shows the corresponding error system converges zero asymptotically.
. Figure 2 shows the corresponding error system converges zero asymptotically.
2) for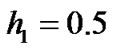 ,
, . Figure 3 shows the corresponding error system converges zero asymptotically.
. Figure 3 shows the corresponding error system converges zero asymptotically.

Figure 1. Examples of connected undirected graph.
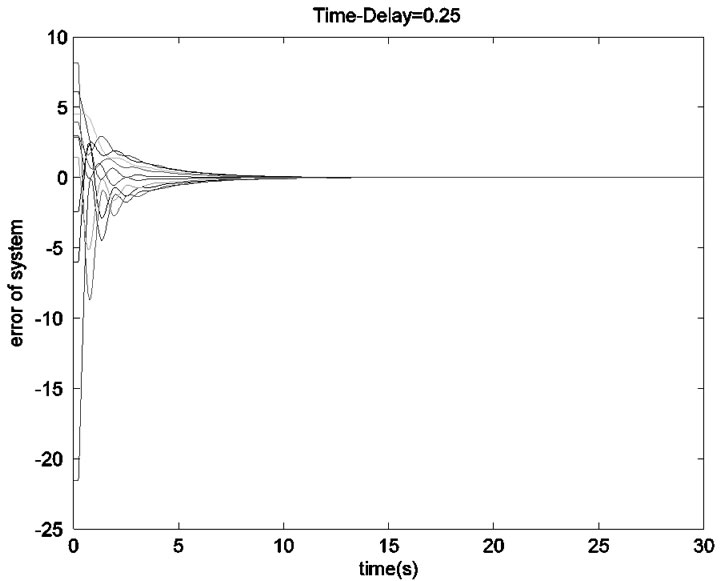
Figure 2. Error system with fixed topology and constant time-delay  with
with  converges to zero asymptotically.
converges to zero asymptotically.

Figure 3. Error system with fixed topology and timevarying delay  with
with  converges to zero asymptotically.
converges to zero asymptotically.
4.2. Examples of Networks with Switching Topology
A finite automation with set of states  is shown in Figure 4, which represents the discrete states of a network with switching topology and time delay as a hybrid system. It starts at the discrete state
is shown in Figure 4, which represents the discrete states of a network with switching topology and time delay as a hybrid system. It starts at the discrete state 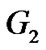 and switches every simulation time step to the next state according to the state machine in Figure 4. For multi-agent system with time-varying communication time delay, we take the derivative of delay
and switches every simulation time step to the next state according to the state machine in Figure 4. For multi-agent system with time-varying communication time delay, we take the derivative of delay . From theorem 2, the feasible maximum delay bound of the system is
. From theorem 2, the feasible maximum delay bound of the system is . And the corresponding feasible solution
. And the corresponding feasible solution ,
,  and
and can be obtained by employing the LMI Tool box in Matlab.
can be obtained by employing the LMI Tool box in Matlab.
Assume the time-varying delay of the error system is . Figure 5 shows the corresponding error system converges zero asymptotically.
. Figure 5 shows the corresponding error system converges zero asymptotically.

Figure 4. A finite automation with three states.

Figure 5. Error system with switching topology and timevarying delay  converges to zero
converges to zero
asymptotically.
5. Conclusions
This paper addresses an average consensus problem of multiagent systems. Undirected networks with fixed and switching network topology coupling multiple timevarying communication delays are considered in this paper. An orthogonal matrix is introduced and the original system is turned into a reduced dimensional system. At the same time, a Lyapunov-Krasovskii function is constructed in the stable analysis. Sufficient conditions in terms of LMI are given to guarantee the system reach average consensus. Moreover, numerical simulation examples are shown to verify the theoretical analysis.
6. Acknowledgment
This work was supported by National Natural Science Foundation of China under the grant 60604001 and 60674081, Hubei Provincial Natural Science Foundation under the grant 2008CDB316 and 2008CDZ046, and Scientific Innovation Team Project of Hubei Provincial College under the grant T200809.
[1] T. Vicsek, A. Czirok, E. Benjacob, I. Cohen, et al., “Novel type of phasetransition in a system of self-driven particles,” Physical Review Letters, Vol. 75, No. 6, pp. 1226–1229, 1995.
[2] A. Jadbabaie, J. Lin, and A. S. Morse, “Coordination of groups of mobile autonomous agents using nearest neighbor rules,” IEEE Transactions on Automatic Control, Vol. 48, No. 6, pp. 988–1001, 2003.
[3] W. Ren, and R. W. Beard, “Consensus seeking in multiagent systems under dynamically changing interaction topologies,” IEEE Transactions on Automatic Control, Vol. 50, No. 5, pp. 655–661, 2005.
[4] L. Moreau, “Stability of multiagent systems with timedependent communication links,” IEEE Transactions on Automatic Control, pp. 169–182, 2005.
[5] R. O. Saber, and R. M. Murray, “Consensus problems in networks of agents with switching topology and time-delays,” IEEEE Transactions on Automatic Control, Vol. 49, No. 9, pp. 1520–1533, 2004.
[6] R. O. Saber and R. M. Murray, “Consensus protocols for networks of dynamic agents,” in Proceedings of American Control Conference, pp. 951–956, June 2003.
[7] Y. Tian and C. Liu, “Consensus of multi-agent systems with diverse input and communication delays,” IEEE Transactions on Automatic Control, Vol. 53, No. 9, pp. 2122–2128, October 2008.
[8] R. O. Saber, J. A. Fax, and R. M. Murray, “Consensus and cooperation in networked multi-agent systems,” in Proceedings of IEEE, Vol. 95, No. 1, pp. 215–233, January 2007.
[9] W. Ren, R. W. Beard, and E. M. Atkins, “Information consensus in multivehicle cooperative control,” IEEE Control Syst. Mag., Vol. 27, No. 2, pp. 71–82, April 2007.
[11] H. Yu, J. G. Jian and Y. J. Wang, “Weighted average consensus for directed networks of multi-agent,” Microcomputer Information, Vol. 23, No. 7, pp. 239–241, Augest 2007.
[10] W. Ren, “Multi-vehicle consensus with a time-varying reference state,” Systems & Control Letters, Vol. 56, No. 7-8, pp. 474–483, July 2007.
[12] D. P. Spanos, R. O. Saber, and R. M. Murray, “Dynamic consensus on mobile networks,” In IFAC World Congr., Prague, Czech Republic, 2005.
[13] Y. Hatano and M. Mesbahi, “Agreement over random networks,” IEEE Transactions on Automatic Control, Vol. 50, No. 11, pp. 1867–1872, November 2005.
[14] R. O. Saber, “Flocking for multi-agent dynamic systems: algorithms and theory,” IEEE Transactions on Automatic Control, Vol. 51, No. 3, pp. 401–420, March 2006.
[15] A. T. Salehi and A. Jadbabaie, “A necessary and sufficient condition for consensus over random networks,” IEEE Transactions on Automatic Control, vol. 53, No. 4, pp. 791–795, April 2008.
[16] G. M. xie and L. wang, “Consensus control for a class of networks of dynamic agents,” Robust Nonliner Control, Vol. 17, pp. 941–959, 2007.
[17] Y. G. Sun, L. Wang and G. M. Xie, “Average consensus in directed networks of dynamic agents with time-varying delays,” in Proceeding of IEEE Conference Decision & Control, Vol. 57, No. 2, pp. 3393–3398, December 2006.
[18] P. Lin and Y. Jia, “Average consensus in networks of multi-agents with both switching topology and coupling time-delay,” Physica A, Vol. 387, No. 1, pp. 303–313, January 2008.
[19] P. Lin, Y. Jia and L. Li, “Distributed robust H∞consensus control in directed networks of agents with time-delay,” Systems & Control Letters, Vol. 57, No. 8, pp. 643–653, Augest 2008.
[20] Y. G. Sun, L. Wang and G. M. Xie, “Average consensus in networks of dynamic agents with switching topologies and multiple time-varying delays,” Systems & Control Letters, Vol. 57, No. 2, pp. 175–183, February 2008.
[21] D. Angeli and P. A. Bliman, “Stability of leaderless discrete-time multiagent systems,” Math. Control Signs Systems, Vol. 18, pp. 293–322, 2006.
[22] A. Papachristodoulou and A. Jadbabaie, “Synchronization in oscillator networks: Switching topologies and non-homogeneous delays,” in Proceedings of the 44th IEEE Conference Decision and Control and the European Control Conference, pp. 5692–5697, December 2005.
[23] A. Papachristodoulou and A. Jadbabaie, “Synchronization in oscillator networks with heterogeneous delays, switching topologies and nonlinear dynamics,” in Proceedings of the 45th IEEE Conference Decision and Control, pp. 4307–4312, December 2006.
[24] N. Biggs, “Algebraic Graph Theory,” Cambridge University Press, Cambridge, U. K., 1974. 6
[25] R. A. Hornn and C. R. Johnson, “Matrix Analysis,” Cambridge University Press, Cambridge, New York, 1985.
NOTES