
1. Introduction
To define the internal structure of elementary particles using the generalized theory of the Maxwell equations [1] it is necessary to solve a system of nonlinear partial differential equations, which is of course a difficult problem. Separating the field into its static and dynamics components [1] simplifies the problem by noting that the static component does not depend on the dynamic one. In the following we will only look at the particle’s static field.
In [1] it is shown that if we assume the model that a particle has a spherically symmetric electric field, then the approximate solution far from the center tends asymptotically to Coulomb’s law as the radius increases, while near the center the two don’t agree. In the following we will solve the problem of determining the magnetic field. Even in this simple case the magnetic field is not spherically symmetric. Far from the center it decays faster than the electric field and the full field becomes essentially purely electric satisfying Coulomb’s law. However, near the center the magnetic field increases and can even become bigger than the electric field; in this case the approximate solutions are not sufficient.
This way, the structure of the static electromagnetic field of the electron is complicated (and multilayered). There are at least two radial boundaries:  and
and , near which the field changes its character. For
, near which the field changes its character. For , the field is practically purely electric and satisfies Coulomb’s law, while for
, the field is practically purely electric and satisfies Coulomb’s law, while for , the magnetic field increases and the approximate solution that we make use of becomes problematic.
, the magnetic field increases and the approximate solution that we make use of becomes problematic.
Future research will have to clarify the internal structure of the electron using a more rigorous solution to the static equations and the dynamic equations [1] .
2. Basic Relations
In [1] they introduce a system of nonlinear partial differential equations that are a generalization of Maxwell equations of electrodynamics with which it seems possible to describe the internal structure of elementary particles. To our point of view, the attractive feature of this theory is that it only makes use of only two vector functions: the electric field 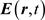 and the magnetic field
and the magnetic field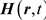 . The multitude of particles is then defined by their configurations.
. The multitude of particles is then defined by their configurations.
The system of four equations for 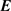 and
and 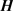 can be written in a more compact and elegant form consisting of only two equations by introducing a new quantity―the complex vector
can be written in a more compact and elegant form consisting of only two equations by introducing a new quantity―the complex vector 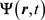 given by
given by

We define a solution 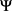 of the form
of the form
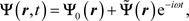
which resembles the function Ψ in Schrödinger’s equation:
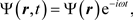
but with the significant difference that in our case the solution is not a scalar, but avector function and has a static component (i.e. independent of time) which is determined by the system of equations [1] :
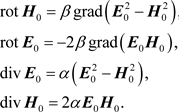 (1)
(1)
From (1) it follows that unlike the Maxwell equations the electric field 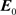 and the magnetic field
and the magnetic field  cannot exist without the other. There exists a magnetic charge (fourth equation) and a magnetic current (second equation) that are defined by the pseudoscalar
cannot exist without the other. There exists a magnetic charge (fourth equation) and a magnetic current (second equation) that are defined by the pseudoscalar ![]() [1] . It is interesting to note that the magnetic monopole (a hypothetical particle) being a magnetic charge and having only one magnetic pole (analogous to an electric charge) was first studied by Dirac but not yet observed experimentally. Considering that the magnetic charge has not been observed experimentally, we can assume that we can set
[1] . It is interesting to note that the magnetic monopole (a hypothetical particle) being a magnetic charge and having only one magnetic pole (analogous to an electric charge) was first studied by Dirac but not yet observed experimentally. Considering that the magnetic charge has not been observed experimentally, we can assume that we can set ![]() (i.e.
(i.e.![]() ). In this case (1) simplifies to
). In this case (1) simplifies to
![]() (2)
(2)
Assuming that the following relation holds:
![]() (3)
(3)
the problem simplifies greatly and Equations (2) take the form
![]() (2’)
(2’)
Considering the second equation in (2’) we have that
![]()
Furthermore, with the help of Hamilton’s operator ![]() and remembering that the Laplacian
and remembering that the Laplacian ![]() we get that the third equation takes the elegant form
we get that the third equation takes the elegant form
![]() (4)
(4)
In the general case the potential ![]() depends on all three spatial coordinates, for that reason the vector
depends on all three spatial coordinates, for that reason the vector ![]() has all three components. In the spherically symmetric case:
has all three components. In the spherically symmetric case:![]() , the field only has one radial component
, the field only has one radial component![]() , depending only on the radius r, and thus the third equation in (2’) for
, depending only on the radius r, and thus the third equation in (2’) for ![]() takes the form
takes the form
![]()
the solution of which is given in [1] :
![]() (5)
(5)
where q is the particle’s charge.
For![]() , far from the particle’s center,
, far from the particle’s center,
(5’)
which agrees with Coulomb’s law. But close to the center, the field differs from Coulomb’s law:
(5’’)
and the boundary between these two limit cases is approximately given by (5) assuming that
or
. Using the radius of the electron
[1] , we have that
This way, for
,
tends to Coulomb’s law, while for
that is not the case.
We now define the static magnetic field of the electron using the first equation in (2’) and plugging in on the right-hand side the value
using (5). We get
or
Assuming that the field
does not depend on the coordinate
, we have that
Integrating this gives us
(6)
For
, far from the particle’s center
Considering (5’) we have that
That is, at great distance from the center the electron’s field is essentially purely electric.
Close to the particle’s center (
)
and considering (5’’) we get that
that is the assumption (3) does not hold, and thus in this case all of the above results are not valid anymore. We analyze the boundary of the permissible region in which hypothesis (3) holds:
For
, the obtained results can be with certain measure of certainty be considered valid, but not for
!
For the results obtained above we can come to the following conclusions:
The structure of the electron’s static electromagnetic field is very complicated (and multilayered) and has at least two boundaries in its radius:
and
which when approached the field changes its structure.
The electron’s field is asymptotically spherically symmetric and electrostatic only at great distances from the particle’s center.
The magnetic static field grows close to the particle’s center and can even become bigger than the electric field.
This way we can recall how V. I. Lenin in his work [3] said way back in 1909 that “The electron is as inexhaustible as the atom…”
3. Note
Analyzing the unusual solutions to the static Equations (1) leads to an interesting concept. Assuming
or
and
(
), from (1) we get
That is, the static field satisfying the above conditions fills up all of space. It’s possible that this is the so called “ether”. Any local fluctuation in time brings about the appearance a variable electromagnetic field that is the creation of a particle. The decay of the fluctuation―to the disappearance of a particle.
This consideration in a certain sense reminds us of Dirac’s 1930 proposal that vacuum represents a space in which at every point there exists an infinite number of electrons of negative energy that forms a background from which it’s possible to calculate all physical quantities [4] .