Periodic Wave Solutions and Solitary Wave Solutions of the (2+1)-Dimensional Korteweg-de-Vries Equatio

Liangwei He¹, Shuanghong Chen^2*

¹Crespi Carmelite High School, Encino, CA, USA.
²Hefei Institutes of Physical Science, Chinese Academy of Sciences, Hefei, China.

DOI: 10.4236/ajcm.2021.114021                

Abstract

In this paper, we investigate the periodic wave solutions and solitary wave solutions of a (2+1)-dimensional Korteweg-de Vries (KDV) equation by applying Jacobi elliptic function expansion method. Abundant types of Jacobi elliptic function solutions are obtained by choosing different coefficients p, q and r in the elliptic equation. Then these solutions are coupled into an auxiliary equation and substituted into the (2+1)-dimensional KDV equation. As a result, a large number of complex Jacobi elliptic function solutions are obtained, and many of them have not been found in other documents. As , some complex solitary solutions are also obtained correspondingly. These solutions that we obtained in this paper will be helpful to understand the physics of the (2+1)-dimensional KDV equation.

Keywords

Nonlinear Evolution Equations, Jacobi Elliptic Function, (2+1)-Dimensional KDV, Periodic Wave Solutions, Solitary Wave Solu-tions

1. Introduction

Solitary wave phenomena were first discovered by British scientist Russell in 1834 [1]. In 1965, it was found that the particle velocity and waveform can remain unchanged after the interaction of solitary waves when solving KdV equation, which is called soliton [2]. After then, the concepts of soliton and solitary waves are widely used in various fields of physics. From hydrodynamics, plasma, optics, condensed matter physics to basic particle physics and even to astrophysics, everywhere [3] - [8], it is all found that there are experimental facts or physical mechanisms for the existence of solitons. Most physical laws can establish mathematical models under certain approximations, and many studies on nonlinear identification can be reduced to nonlinear evolution equations (NLEEs) finally. Therefore, seeking their exact solutions such as the breather, solitary wave and periodic wave solutions is very significant for the exploration of related nonlinear problems, which also has always been an important focus on the study of mathematics and physics. Significant progress has been made in recent centuries and many strong and effective methods have been proposed in the documents to obtain the exact solutions of NLEEs. For example, algebraic method [9], homogeneous balance method [10], tanh/sech method and the extended tanh/coth method [11] [12], the sine–cosine method [13], F-expansion method [14] [15], Jacobi elliptic function expansion method [16] [17], Expfunction method [18], the modified extended mapping method [19] [20] [21], auxiliary equation method [22] [23] [24], and so on.

In this paper, we consider revealing the new periodic wave and solitary solutions for the (2+1)-dimensional KDV equation [25] [26] [27]

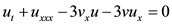(1)

(2)

which was first derived by Boiti et al. by using the idea of the weak Lax pair [26]. If v = u and y = x, Equation (1) degenerates into the (1 + 1)-dimensional KdV equation [2]. The (2+1) dimensional case involves more complex nonlinear phenomena, and this scan describes certain physics phenomena in plasmas and fluids, where 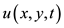and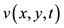 are real differential wave functions depending on the 2-dimensional space variable x and yand 1-dimensional time variablet. Equation (1) was investigated in different methods. In Refs. [28] and [27], the variable separation solution of Equation (1) was obtained and some special types of solitary wave solutions were given in Ref. [29]. In Ref. [30], the exact periodic cross-kink wave solutions are obtained by using Hirota’s bilinear form and a generalized three-wave approach. In Ref. [30] Higherorder KDV equation is considered, many travelling solitary wave solutions are found.

These methods are effective in solving (2+1)-dimensional KdV equation, however, there are still some new types of solutions to be explored. Here a new auxiliary equation is developed to construct abundant periodic wave solutions of (2+1)-dimensional KDV equation. With the help of the elliptic equation, many new types of solutions are obtained.

2. Method

We assume Equation (1) and Equation (2) have a traveling wave solution by taking

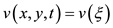, , (3)

where ω is a wave parameter to be determined. Substituting Equation (3) into Equation (1) and Equation (2) yields

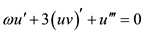(4)

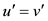(5)

where u' means du/dξ and v' means dv/dξ. Integrating the above two equation once and setting the integration constant in Equation (4) to zero yields

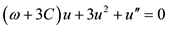(6)

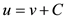(7)

It is assumed that Equation (4) has the following formal solution

(8)

where a_i, b_i, c_i and d_i are constants to be determined later. The positive integer n can be determined by the homogeneous balance method in Equation (6). f(ξ) expresses the solutions of the following elliptic equation

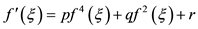(9)

where p, q, r are parameters to be selected for Jacobi elliptic function. By selecting different p, q, r, the different Jacobi elliptic function solutions of Equation (9) are shown in Table 1. Furthermore, these solutions include hyperbolic function solutions when 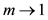and trigonometric function solutions when.

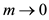where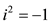. Substituting Equation (8) and Equation (9) into (6), and setting the coefficients of 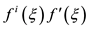to zero, then solving the resulting equations and using Table 1, the following new type of periodic wave solutions of Equation (4) can be obtained.

Case 1

(10)

where,.

Case 2

(11)

where,.

Case 3

(12)

where,.

Case 4

(13)

where,.

Case 5

Table 1. Jacobi elliptic function solutions for Equation (9).

(14)

where,.

These solutions are a set of solutions containing a large number of Jacobielliptic functions, hyperbolic functions and trigonometric functions according to Table 1. If, , , , , , , , , , and, the Equation (10) and Equation (11) are the solutions that can be obtained by Refs. [16] [17]. If, , and, the solutions of (2+1)-dimensional KDV equation are shown as

(15)

where,.

(16)

where,.

(17)

where,.

(18)

where,.

(19)

where,.

These five types of periodic wave solutions of (2+1)-dimensional KDV equation are shown as Figure 1, where m= 0.2, t= 0, C= 0 and “−” are chosen in Equations (17), (18) and (19). It can be seen in Figure 1 that the solution expressed by Equation (15) changes periodically with the spatial position and the amplitude will change accordingly, while the solution expressed by Equation (16) has no change in period, but the amplitude changes greatly compared with Equation (15). The period of the solution expressed by Equation (17) is longer than that expressed in Equation (15), and the amplitude increases slightly. The period of the solution expressed by Equation (18) is similar to that expressed

Figure 1. Periodic wave solutions of (2+1)-dimensional KDV equation when. (a) solution expressed by Equation (15), (b) solution expressed by Equation (16), (c) solution expressed by Equation (17), (d) solution expressed by Equation (18), (e) solution expressed by Equation (19), where m= 0.2, t= 0, C= 0 and “−” are chosen in Equations (17), (18) and (19).

by Equation (17) while the amplitude increases greatly. The period and amplitude of the solution expressed in Equation (19) are similar to that expressed by Equation (18).

If, the corresponding solitary wave solutions of (2+1)-dimensional KDV equation are shown as

(20)

where,.

(21)

where,.

(22)

where,.

(23)

where,.

(24)

where,.

These five types of solitary wave solutions of (2+1)-dimensional KDV equation are shown in Figure 2, where C= 0, t= 0, “−” is chosen in Equation (23), “+” is chosen in Equation (22) and “+” is chosen for the previous “±” and “−” is chosen for the next. It can be seen that these five solitary wave solutions are all

Figure 2. Corresponding solitary wave solutions of (2+1)-dimensional KDV equation when. (a) solution expressed by Equation (20), (b) solution expressed by Equation (21), (c) solution expressed by Equation (22), (d) solution expressed by Equation (23), (e) solution expressed by Equation (24), where C= 0, t= 0, “−” is chosen in Equations (23), “+” is chosen in Equations (22) and “+” is chosen for the previous “±” and “−” is chosen for the next.

bell-type, but there are some differences in amplitude and phase of the solitary wave.

If, , and, the solutions of (2+1)-dimensional KDV equation are shown as

(25)

where,.

(26)

where,.

(27)

where,.

(28)

where,.

(29)

where,.

These five types of periodic wave solutions of (2+1)-dimensional KDV equation are shown in Figure 3. As shown in the figure, Equations (25), (26) and Equations (27), (28) have similar periodic wave solutions in terms of period and amplitude respectively. While the period of the solution expressed by Equation (29) becomes smaller and the amplitude becomes larger compared with the previous four groups of solutions.

If, the solutions expressed by Equations (25) and (26) have no corresponding hyperbolic function solutions, the solutions of the rest three groups of corresponding solitary wave solutions of (2+1)-dimensional KDV equation are as follows

(30)

Figure 3. Periodic wave solutions of (2+1)-dimensional KDV equation when. (a) solution expressed by Equation (25), (b) solution expressed by Equation (26), (c) solution expressed by Equation (27), (d) solution expressed by Equation (28), (e) solution expressed by Equation (29), where m= 0.2, t= 0, C= 0 and “−” are chosen in Equations (27), (28) and (29).

where,.

(31)

where,.

(32)

where,.

These three types of solitary wave solutions of (2+1)-dimensional KDV equation

Figure 4. Corresponding solitary wave solutions of (2+1)-dimensional KDV equation when. (a) solution expressed by Equation (20), (b) solution expressed by Equation (21), (c) solution expressed by Equation (22), where C= 0, t= 0, “−” is chosen in Equations (31)and (32), “+” is chosen in Equation (30).

are shown as Figure 4, where C= 0, t= 0, “−” is chosen in Equations (31) and (32), “+” is chosen in Equation (30). It can be seen that these three solitary wave solutions are all bell-type, and there are still some differences in the amplitude and phase of the solitary wave.

There are still a large number of periodic wave solutions of (2+1)-dimensional KDV equation, according to Equations (9), (10), (11), (12), (13), (14) and Table 1. These solutions may also have solitary solutions under the conditions of. The corresponding solutions of v(ξ) can be obtained from Equation (7). Limited to this scope, we will not give examples one by one.

3. Conclusion

In this paper, we apply the extended Jacobi elliptic function expansion method to explore the exact solution of the (2+1)-dimensional KDV equation. With the cooperation of the auxiliary Equations (8), (9) and its Jacobi elliptic function solution set Table 1, we have constructed abundant and new periodic wave solutions for (2+1)-dimensional KDV equation. Under the conditions of, the corresponding solitary solutions are also obtained. We also study the images of periodic wave and solitary wave solutions in different phase spaces. It is found that different types of periodic wave solutions have different periods and amplitudes, which implies that the corresponding periodic wave can be generated under certain phase space conditions. Several solitary wave solutions we explored are all bell-type solitary waves, and there are only some differences in the amplitude and phase of the solitary wave. This method has broad application prospects for constructing abundant periodic wave solutions and solitary wave solutions, and can be used as a useful guide for a wide range of nonlinear problems in mathematical and physical research. The solutions we obtained in this paper will be helpful to understand the physics of the (2+1)-dimensional KDV equation.

Conflicts of Interest

The authors declare no conflicts of interest regarding the publication of this paper.

References

[1]	Ablowitz, M. and Clarkson, P. (1991) Solitons, Nonlinear Evolution Equations and Inverse Scattering. Cambridge University Press, Cambridge. https://doi.org/10.1017/CBO9780511623998
[2]	Gardner, C.S., Greene, J.M., Kruskal, M.D. and Miura, R.M. (1967) Method for Solving Korteweg-Devries Equation. Physical Review Letters, 19, 1095-1097. https://doi.org/10.1103/PhysRevLett.19.1095
[3]	Guo, H.D., Xia, T.C. and Hu, B.B. (2020) High-Order Lumps, High-Order Breathers and Hybrid Solutions for an Extended (3+1)-Dimensional Jimbo-Miwa Equation in Fluid Dynamics. Nonlinear Dynamics, 100, 601-614. https://doi.org/10.1007/s11071-020-05514-9
[4]	Lan, Z.Z. and Guo, B.L. (2020) Nonlinear Waves Behaviors for a Coupled Generalized Nonlinear Schrödinger-Boussinesq System in a Homogeneous Magnetized Plasma. Nonlinear Dynamics, 100, 3771-3784. https://doi.org/10.1007/s11071-020-05716-1
[5]	Biswas, A., Ekici, M., Sonmezoglu, A. and Belic, M.R. (2019) Solitons in Optical Fiber Bragg Gratings with Dispersive Reflectivity by Extended Trial Function Method. Optik, 182, 88-94. https://doi.org/10.1016/j.ijleo.2018.12.156
[6]	Seadawy, A.R., Lu, D.C., Nasreen, N. and Nasreen, S. (2019) Structure of Optical Solitons of Resonant Schrodinger Equation with Quadratic Cubic Nonlinearity and Modulation Instability Analysis. Physica A, 534, Article ID: 122155. https://doi.org/10.1016/j.physa.2019.122155
[7]	Abdoud, M.A., Owyed, S., Abdel-Aty, A., Raffan, B.M. and Abdel-Khalek, S. (2020) Optical Soliton Solutions for a Space-Time Fractional Perturbed Nonlinear Schrödinger Equation Arising in Quantum Physics. Results in Physics, 16, Article ID: 102895. https://doi.org/10.1016/j.rinp.2019.102895
[8]	Peng, W.Q., Tian, S.F. and Zhang, T.T. (2019) Dynamics of the Soliton Waves, Breather Waves, and Rogue Waves to the Cylindrical Kadomtsev-Petviashvili Equation in Pair-Ion-Electron Plasma. Physics of Fluids, 31, Article ID: 102107. https://doi.org/10.1063/1.5116231
[9]	Arshad, M., Seadawy, A.R., Lu, D.C. and Wang, J. (2017) Travelling Wave Solutions of Drinfel’d-Sokolov-Wilson, Whitham-Broer-Kaup and (2+1)-Dimensional Broer-Kaup-Kupershmit Equations and Their Applications. Chinese Journal of Physics, 55, 780-797. https://doi.org/10.1016/j.cjph.2017.02.008
[10]	Seadawy, A.R. (2016) Stability Analysis Solutions for Nonlinear Three-Dimensional Modified Korteweg-de Vries-Zakharov-Kuznetsov Equation in a Magnetized Electron-Positron Plasma. Physica A, 455, 44-51. https://doi.org/10.1016/j.physa.2016.02.061
[11]	Seadawy, A.R. (2014) Stability Analysis for Zakharov-Kuznetsov Equation of Weakly Nonlinear Ion-Acoustic Waves in a Plasma. Computers & Mathematics with Applications, 67, 172-180. https://doi.org/10.1016/j.camwa.2013.11.001
[12]	Seadawy, A.R. (2014) Stability Analysis for Two-Dimensional Ion-Acoustic Waves in Quantum Plasmas. Physics of Plasmas, 21, Article ID: 052107-1. https://doi.org/10.1063/1.4875987
[13]	Yan, C.T. (1996) A Simple Transformation for Nonlinear Waves. Physics Letters A, 224, 77-84. https://doi.org/10.1016/S0375-9601(96)00770-0
[14]	Liu, J.B. and Yang, K.Q. (2004) The Extended F-Expansion Method and Exact Solutions of Nonlinear PDEs. Chaos, Solitons & Fractals, 22, 111-121. https://doi.org/10.1016/j.chaos.2003.12.069
[15]	Zhang, S. (2007) Application of Exp-Function Method to a KdV Equation with Variable Coefficients. Physics Letters A, 365, 448-453. https://doi.org/10.1016/j.physleta.2007.02.004
[16]	Liu, S.K., Fu, Z.T., Liu, S.D. and Zhao, Q. (2001) Jacobi Elliptic Function Expansion Method and Periodic Wave Solutions of Nonlinear Wave Equations. Physics Letters A, 289, 69-74. https://doi.org/10.1016/S0375-9601(01)00580-1
[17]	Fu, Z.T., Liu, S.K., Liu, S.D. and Zhao, Q. (2001) New Jacobi Elliptic Function Expansion and New Periodic Solutions of Nonlinear Wave Equations. Physics Letters A, 290, 72-76. https://doi.org/10.1016/S0375-9601(01)00644-2
[18]	Shek, E.C.M. and Chow, K.W. (2008) The Discrete Modified Korteweg-de Vries Equation with Non-Vanishing Boundary Conditions: Interactions of Solitons. Chaos, Solitons & Fractals, 36, 296-302. https://doi.org/10.1016/j.chaos.2006.06.036
[19]	Li, H.M. (2002) Searching for the (3+1)-Dimensional Painleve Integrable Model and Its Solitary Wave Solution. Chinese Physics Letters, 19, 745-747. https://doi.org/10.1088/0256-307X/19/6/301
[20]	Yomba, E. (2004) On Exact Solutions of the Coupled Klein-Gordon-Schrodinger and the Complex Coupled KdV Equations Using Mapping Method. Chaos, Solitons & Fractals, 21, 209-229. https://doi.org/10.1016/j.chaos.2003.10.028
[21]	Li, H.M. (2005) New Exact Solutions of Nonlinear Gross-Pitaevskii Equation with Weak Bias Magnetic and Time-Dependent Laser Fields. Chinese Physics, 14, 251-256.
[22]	Wu, G., Han, J., Zhang, W. and Zhang, M. (2007) New Periodic Wave Solutions to Nonlinear Evolution Equations by the Extended Mapping Method. Physica D: Nonlinear Phenomena, 229, 116-122. https://doi.org/10.1016/j.physd.2007.03.015
[23]	Sirendaoreji and Sun, J. (2003) Auxiliary Equation Method for Solving Nonlinear Partial Differential Equations. Physics Letters A, 309, 387-396. https://doi.org/10.1016/S0375-9601(03)00196-8
[24]	Sirendaoreji (2004) New Exact Travelling Wave Solutions for the Kawahara and Modified Kawahara Equations. Chaos, Solitons & Fractals, 19, 147-150. https://doi.org/10.1016/S0960-0779(03)00102-4
[25]	Clarkson, P.A. and Mansfield, E.L. (1995) Symmetry Reductions and Exact-Solutions of Shallow-Water Wave-Equations. Acta Applicandae Mathematica, 39, 245-276. https://doi.org/10.1007/BF00994636
[26]	Boiti, M., Leon, J.J.P., Manna, M. and Pempinelli, F. (1986) On the Spectral Transform of A Korteweg-Devries Equation in 2 Spatial Dimensions. Inverse Problems, 2, 271-279. https://doi.org/10.1088/0266-5611/2/3/005
[27]	Lou, S.Y. and Ruan, H.Y. (2001) Revisitation of the Localized Excitations of the (2+1)-Dimensional KdV Equation. Journal of Physics A: Mathematical and General, 34, 305-316. https://doi.org/10.1088/0305-4470/34/2/307
[28]	Tang, X.Y. and Lou, S.Y. (2002) A Variable Separation Approach to Solve the Integrable and Nonintegrable Models: Coherent Structures of the (2+1)-Dimensional KdV Equation. Communications in Theoretical Physics, 38, 1-8. https://doi.org/10.1088/0253-6102/38/1/1
[29]	Liu, J.G., Du, J.Q., Zeng, Z.F. and Ai, G.P. (2016) Exact Periodic Cross-Kink Wave Solutions for the New (2+1)-Dimensional KdV Equation in Fluid Flows and Plasma Physics. Chaos, 26, Article ID: 103114. https://doi.org/10.1063/1.4966020
[30]	Xiang, C. and Wang, H. (2019) Travelling Solitary Wave Solutions to Higher Order Korteweg-de Vries Equation. Open Journal of Applied Sciences, 9, 354-360. https://doi.org/10.4236/ojapps.2019.95029