Regularization and Choice of the Parameter for the Third Kind Nonlinear Volterra-Stieltjes Integral Equation Solutions ()
1. Introduction
Differential and integral equations theory considering fractional order are relevant in mathematics nowadays, which have numerous applications in various fields, physics, mechanics, control theory, engineering, electrochemistry, bioengineering, viscoelasticity, porous media [1] [2] [3]. Solution of the nonlinear integral equation of Volterra-Stieltjes type, and the method is based on an equivalence relation between the fractional differential equation, and Volterra–Stieltjes integral equation of the second kind was also reported in our previous works [4] [5]. Here we are describing regularization and the choice of the parameter for nonlinear Volterra-Stieltjes integral equations of the third kind.
Let us consider the equation,
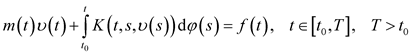 (1)
(1)
where 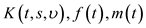 are given functions,
are given functions, 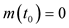 ,
, 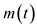 are non-decreasing continuous functions on
are non-decreasing continuous functions on ,
, 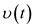 is an unknown function on
is an unknown function on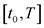 ,
, 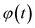 is an increasing continuous function
is an increasing continuous function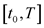 .
.
Along with Equation (1), we will consider the equation
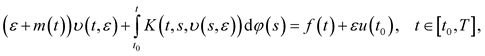 (2)
(2)
where 0 < ε is a small parameter,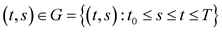 .
.
Everywhere we assume that 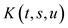 is representable as
is representable as
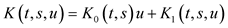 ,
,
where
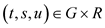 (3)
(3)
Various questions of the theory of the integral equations were investigated in many works. In particular, in [6] linear integral equations of the second kind and their systems on finite and infinite intervals were studied. A survey of results on Volterra integral equations of the second kind was described [7]. The existence of a multiparameter family of solutions proved for linear Volterra integral equations of the first and third kind with smooth kernels [8]. But the fundamental results for the Fredholm integral equations of the first kind were obtained [9], where regularizing operators according to M.M. Lavrentyev were constructed for solving the linear Fredholm integral equations of the first kind. In [10] and [11], Volterra equations of the first kind and inverse problems were investigated. The uniqueness theorems were proved and regularizing operators were constructed according to M.M. Lavrentyev for systems of linear and nonlinear Volterra integral equations of the first kind with nonsmooth matrix kernels [12] [13]. The systems of nonlinear Volterra integral equations of the third kind, uniqueness theorems were proved and regularizing operators were constructed according to M.M. Lavrentyev [14]. In [15], the uniqueness theorems were proved for systems of linear Fredholm integral equations of the third kind, and regularizing operators were constructed according to M.M. Lavrentyev. In [16], based on a new approach, the questions of existence and uniqueness of solutions for systems of linear Fredholm integral equations of the third kind with a singularity at one point on a finite interval were investigated. Based on the approach proposed in [17], the class of Fredholm integral equations of the third kind on a finite interval was studied. Based on the approaches proposed in [18] [19], an improved new approach was developed for studying systems of linear and nonlinear Fredholm integral equations of the third kind with multipoint singularities on a finite interval. In [20], according to the concept of the derivative of a function concerning an increasing function introduced in [19], linear and nonlinear Volterra-Stieltjes integral equations of the first and second kind were investigated. For the solution of one class of linear Volterra, and Volterra-Stieltjes integral equations of the third kind, a regularizing operator was constructed according to MM. Lavrentyev and proved the uniqueness theorem [21] [22]. The regularization parameter is chosen for solving the linear Volterra-Stieltjes integral equation of the third kind [4].
Here, to solve the nonlinear Volterra-Stieltjes integral equation of the third kind (1), a regularizing operator which was constructed according to M.M. Lavrentyev, a uniqueness theorem proved, and a regularization parameter was chosen.
Suppose the following conditions are met:
a)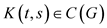 ,
, 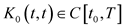 ,
, 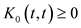 at
at 
b) If the condition ![]() for any function
for any function![]() , the following equation is fair:
, the following equation is fair:
![]()
where ![]() is a known positive number.
is a known positive number.
c) ![]()
at![]() ,
,
at ![]() for any
for any ![]() following equation is fair:
following equation is fair:
![]()
where ![]() is a known positive number.
is a known positive number.
Here ![]() is the space of all continuous functions
is the space of all continuous functions![]() , determined on
, determined on ![]()
with norm
![]()
We will denote ![]() linear space of all functions
linear space of all functions![]() , determined on
, determined on ![]() and satisfying condition
and satisfying condition
![]()
where M is a positive constant depending on![]() , but not on thet and s.
, but not on thet and s.
In further the lemmas 1, 2 and 3 are used,
Lemma 1.
Let conditions a) holds and
![]() (4)
(4)
If![]() , then
, then
![]() (5)
(5)
where
![]()
![]()
Lemma 2.
Let conditions a), b) hold and
![]()
The following estimate is fair
![]() (6)
(6)
Lemma 3.
Let conditions a), c) hold and
![]() (7)
(7)
If that, the following estimation is fair
![]() (8)
(8)
Theorem 1.
Let the conditions a), b), c) be satisfied, and Equation (1) has a solution
![]()
Then solution ![]() of the Equation (2) converges in the norm
of the Equation (2) converges in the norm ![]() to
to ![]() for
for ![]() and the estimate
and the estimate
![]() (9)
(9)
holds. Where
![]()
![]()
Further let us consider that function ![]() and number
and number![]() , in agreement with
, in agreement with
![]() (10)
(10)
where ![]() and
and ![]() are constant values.
are constant values.
Let us consider the equation
![]() (11)
(11)
From (2) by subtracting formula (11) and introducing the notation
![]() (12)
(12)
We have
![]() (13)
(13)
Equation (13) can be written in the form
![]() (14)
(14)
Using the kernel resolvents![]() , and generalized Dirichlet formula [15], Equation (14) is reduced to the following equivalent equation
, and generalized Dirichlet formula [15], Equation (14) is reduced to the following equivalent equation
![]() (15)
(15)
where ![]() was determined in the lemma 2,
was determined in the lemma 2,
![]() (16)
(16)
![]() (17)
(17)
It is not hard to be convinced that
![]() (18)
(18)
Taking into account condition c) and identity (18), from (17) we have
![]() (19)
(19)
Based on the Equation (10), from (16) we have
![]() (20)
(20)
Based on Lemma 2, ![]() estimate (6) is fair.
estimate (6) is fair.
By estimating![]() . Taking into account conditions a) and c) from (19) we obtain
. Taking into account conditions a) and c) from (19) we obtain
![]()
![]() (21)
(21)
Based on the estimate (20), (6), (21) and taking into account (12), from (15) we have
![]() (22)
(22)
Further, based on the generalized Gronwall-Bellman inequality [6], from (22) we obtain the following estimate
![]() (23)
(23)
where
![]() (24)
(24)
It is known that
![]()
Here taking into account (23), we have
![]() (25)
(25)
where number ![]() determined by the formula (24).
determined by the formula (24).
![]() (26)
(26)
where ![]() , numbers K, M and
, numbers K, M and ![]() were determined in Theorem 1.
were determined in Theorem 1.
Assuming ![]() from (26) we obtain
from (26) we obtain
![]() (27)
(27)
where numbers ![]() are determined in Equations (24) and (26).
are determined in Equations (24) and (26).
Thus, Theorem 2 was proved.
Theorem 2. Let conditions a), b), c) be satisfied, and Equation (1) has a solution
![]()
![]()
Then the solution ![]() in Equation (11)
in Equation (11) ![]() converges at the norm
converges at the norm
![]() to
to![]() .
.
Wherein, Estimate (27) is fair.
Example. Let us consider Equations (1) at
![]()
i.e., let us look at the following equation
![]() (27)
(27)
In this case, conditions a), b), c) of Theorems 1 and 2 are satisfied. Since at conditions![]() ,
, ![]() , the following estimate is fair
, the following estimate is fair
![]()
Here![]() .
.
At ![]() for
for ![]()
the following estimate is fair
![]()
2. Conclusions
After choosing the regularization parameter for solving nonlinear Volterra-Stieltjes integral equations of the third kind, we made the following conclusions:
1) Sufficient uniqueness conditions and regularization of solutions of nonlinear Volterra-Stieltjes integral equations of the third kind were found;
2) The choice of the regularization parameter for solving a class of Volterra-Stieltjes nonlinear equations of the third kind was considered;
3 Uniqueness theorems for solutions proved for the nonlinear Volterra-Stieltjes integral equations of the third kind.
Acknowledgements
The authors are thankful to Professor A. Asanov for discussions and advice in solving equations.