Bio-Electromagnetics without Fields: The Effect of the Vector Potential

Andras Szasz

Biotechnics Department, St. Istvan University, Budaors, Hungary.

DOI: 10.4236/ojbiphy.2021.112007                

Abstract

Numerous considerations deal with specialties of bioelectromagnetic effects, including the force-free and field-free interactions. The fact that bioelectromagnetic phenomena consist of effects without mechanical forces and even without measurable fields looks impossible in the simple considerations. However, the stochastic fluctuations cause surprising results, with scientifically proven bioelectromagnetism in field-free conditions. In the first steps, we show the scalar and vector potentials’ specialties instead of electric and magnetic fields defined by the well-known Maxwellian equations. The vanishing of the fields is connected to the potentials’ stochastic fluctuations, the noises control the “zero-ground”. The result shows a possibility of a wave that has no attenuation during its transmission through the material. In this meaning, the result is similar to the consequences of the scalar-wave (SW) considerations. The structural changes follow a particular noise spectrum (called pink-noise or 1/f noise), which keeps the entropy constant in a broad range of scaling magnification.

Keywords

Vector-Potential, Scalar-Potential, Stochastic-Processes, Field-Free Effects, Curl-Free Fields, Axial-Vector, Life, Homeostasis, Entropy, 1/f Noise

1. Introduction

The scientific research on electromagnetic effects on biological systems involves numerous theoretical and practical aspects in the last couple of centuries. Electric and magnetic fields, depending on their intensity, frequency, and gradients, affect the biological processes, including the immune cells [1]. The magnetic field could support chemotherapy in oncology [2], despite missing observable clinical changes, the improvement of the patients’ quality of life is expected. On the other hand, the current research shows the active role of the magnetic vector potential in biological processes [3]. The effect of weak magnetic fields is frequently described with a vector potential in several biological studies of [4] [5]. The vector potential can modify the quantum-states of the water [6], which could modify the complete chain-processes in living objects, governed by the phosphorylation catalyzing metal ions with magnetic nuclei [7].

Alternative medicine frequently uses the idea of water-state modification considerations [8], sometimes applying unproven effects. Controversial discussions about the “silent” bioelectromagnetics as “energy-medicine”, [9] with force-free action on the viability of bacteria E. coli [10], the “electrosmog” [11] [12], the “new biophysical field”, “force-free actions” [13], “scalar-wave effects” [14], “subtle energies” [15] generate heated debates. Intense debates with opposing opinion on physical [16] and mathematical basis [17] [18] for evidence-less applications were published. Direct investigation of quackery [19] and the variants of electromagnetic methods are questioned [20] [21]. Despite some spectacular results of the magnetic therapies, solid scientific proof and clinical evidence are missing, but the public’s hopes keep alive even the poorly documented cases. The weak proofs well support the medical skepticism [22] [23].

The famous Maxwell equations [24] base the classical electrodynamics. Maxwell revolutionary introduced new physical quantities: the electric ( $\mathcal{E}$ ) and the magnetic ( $\mathcal{H}$ ) fields. The standing (free charge density $\rho$ ) and moving (current density $j$ ) charges in vacuum form the sources of the fields:

$div\left(\mathcal{E}\right)=\frac{1}{{\epsilon }_0}\rho$ and $div\left(\mathcal{H}\right)=0$ (1)

and the sources of the field’s whirls in vacuum:

$rot\left(\mathcal{E}\right)=-\frac{\partial \mathcal{H}}{\partial t}$ and $rot\left(\mathcal{H}\right)=j+{\epsilon }_0\frac{\partial \mathcal{E}}{\partial t}$ (2)

where ${\epsilon }_0\cong 8.854\times {10}^{-12}\text{F}/\text{m}$ is a universal constant.

The conservation law of the charge:

$\frac{\partial \rho }{\partial t}+div\left(j\right)=0$ (3)

Sources and whirls define a vector-field which mathematical scheme makes the Maxwell Equations (1)-(2) complete to determine the two field-vectors $\mathcal{E}$ and $\mathcal{H}$. In presence of materials (like living objects, too), we have to take into account the atomic and molecular structures, which have bounded charges. In the case of the presence of materials, new sources appear. Introducing the electric-(P) and magnetic-(M) polarization vectors, we get the electric displacement field (D) and the magnetic induction (B):

$D={\epsilon }_0\mathcal{E}+P$ and $B={\mu }_0\mathcal{H}+M$ (4)

and ${\mu }_0\cong 1.256\times {10}^{-6}\text{N}/{\text{A}}^{\text{2}}$, is a universal constant.

Generally, we assume P and M depend on the $\mathcal{E}$ and B fields respectively, so their Taylor’s series:

$\begin{array}{l}P\left(\mathcal{E}\right)={\left(P\left(\mathcal{E}\right)\right)}_{\mathcal{E}=0}+{\left(\frac{\partial P}{\partial \mathcal{E}}\right)}_{\mathcal{E}=0}\mathcal{E}+\frac{1}{2}{\left(\frac{{\partial }^{2}P}{\partial {\mathcal{E}}^2}\right)}_{\mathcal{E}=0}{\mathcal{E}}^2+\frac{1}{6}{\left(\frac{{\partial }^{3}P}{\partial {\mathcal{E}}^3}\right)}_{\mathcal{E}=0}{\mathcal{E}}^3+\cdot \cdot \cdot \\ \text{and}\\ M\left(\mathcal{H}\right)={\left(M\left(\mathcal{H}\right)\right)}_{\mathcal{H}=0}+{\left(\frac{\partial M}{\partial \mathcal{H}}\right)}_{\mathcal{H}=0}\mathcal{H}+\frac{1}{2}{\left(\frac{{\partial }^{2}M}{\partial {\mathcal{H}}^2}\right)}_{\mathcal{H}=0}{\mathcal{H}}^2\\ +\frac{1}{6}{\left(\frac{{\partial }^{3}M}{\partial {\mathcal{H}}^3}\right)}_{\mathcal{H}=0}{\mathcal{H}}^3+\cdot \cdot \cdot \end{array}$ (5)

The practical engineering simplifies (5) by considering only the linear term:

$P\left(\mathcal{E}\right)={\left(\frac{\partial P}{\partial \mathcal{E}}\right)}_{\mathcal{E}=0}\mathcal{E}$ and $M\left(\mathcal{H}\right)={\left(\frac{\partial M}{\partial \mathcal{H}}\right)}_{\mathcal{H}=0}\mathcal{H}$ (6)

consequently

$\begin{array}{l}D={\epsilon }_0\left[1+\frac{1}{{\epsilon }_0}{\left(\frac{\partial P}{\partial \mathcal{E}}\right)}_{\mathcal{E}=0}\right]\mathcal{E}={\epsilon }_0{\epsilon }_r\mathcal{E}\text{and}\\ B={\mu }_0\left[1+\frac{1}{{\mu }_0}{\left(\frac{\partial M}{\partial \mathcal{H}}\right)}_{\mathcal{H}=0}\right]\mathcal{H}={\mu }_0{\mu }_r\mathcal{H}\end{array}$ (7)

where ${\epsilon }_r$ and ${\mu }_r$ (relative permittivity and relative permeability, respectively) denote the material parameters, which are constant in the linear approach. The linearity requests very special conditions: homogeneous materials, adequately small fields, and no permanent/remnant polarization/magnetization, and additionally the $P\left(\mathcal{E}\right)$ and $M\left(\mathcal{H}\right)$ functions must be smoothly continuous (existing derivatives are necessary).

2. Bio-Electromagnetism

First, confirm that you have the correct template for your paper size. The living material is inherently highly polarized and extremely heterogeneous and has various non-linear processes (physiological feedback). The linear approach does not describe the real, heterogeneous, non-linear living phenomena. The correct formulation of the complete Maxwell equations for living matter uses (4):

$div\left(\mathcal{E}\right)=\frac{\rho }{{\epsilon }_0}-div\left(P\right)$ (8)

$div\left(B\right)=0$ (9)

$rot\left(\mathcal{E}\right)=-\frac{\partial B}{\partial t}$ (10)

$rot\left(B\right)={\mu }_{0}j+{\mu }_0{\epsilon }_0\frac{\partial \mathcal{E}}{\partial t}+{\mu }_0\frac{\partial P}{\partial t}+{\mu }_{0}rot\left(M\right)$ (11)

Define the effective sources by comparison (1)-(2) with (8)-(11):

${\rho }_{eff}=\rho -{\epsilon }_{0}div\left(P\right)$ (12)

and

$j_{eff}=j+\frac{\partial P}{\partial t}+rot\left(M\right)$ (13)

Instead of the free-charge conservation (3) effective charge considering the presence of the material makes connection between the effective values:

$\frac{\partial {\rho }_{eff}}{\partial t}+div\left(j_{eff}\right)=C_{eff}$ (14)

where $C_{eff}$ depends on the derivatives of the $P$ and $M$ vectors. When the derivatives vanish, the free-charge conservation (see (3)) remains in force, $C_{eff}=0$. The zero divergence in (9) (source-less condition because of magnetic monopole does not exist) defines a new quantity by introducing a vector-field ( $A$, called magnetic vector potential)

$B=rot\left(A\right)$ (15)

which automatically satisfies (9), because of $div\left(rot\left(A\right)\right)\equiv 0$. The induction flux Ф of an open surface S, defines the physical meaning of the vector potential A having special role in bio-systems [25]. The Stokes’ theorem gives the induction flux (Ф) encircled by the curve

$\Phi ={\displaystyle {\int }_{S}B\text{d}S}={\displaystyle {\int }_{S}rot\left(A\right)\text{d}S}={\displaystyle {\int }_{L}A\text{d}r}$ (16)

where, the L circumflex of open surface S. Therefore, in the closed contour-line integral of vector potential gives Ф. On the one hand, the magnetic flux density in accordance with Faraday’s induction law (10) generates Eddy-current loops of $\mathcal{E}$. Let us enter the relationship using (15) and (10):

$rot\left(\mathcal{E}+\frac{\partial A}{\partial t}\right)=0$ (17)

which obviously introduces the $\phi$ scalar potential:

$\left(\mathcal{E}+\frac{\partial A}{\partial t}\right)=-grad\left(\phi \right)$ (18)

To define the scale of the potentials, we usually fix the $divA$ by the Lorentz condition:

$divA+{\epsilon }_0{\mu }_0\frac{\partial \phi }{\partial t}=0$ (19)

The wave equations of the potentials:

$\begin{array}{l}\Delta A-{\epsilon }_0{\mu }_0\frac{{\partial }^{2}A}{\partial t^2}={\mu }_0{j}_{eff}\\ \Delta \phi -{\epsilon }_0{\mu }_0\frac{{\partial }^2\phi }{\partial t^2}=-\frac{{\rho }_{eff}}{{\epsilon }_0}\end{array}$ (20)

The simple realization of “pure” A vector is the space outside of an infinite cylindrical solenoid with $r_0$ radius supplied by I current in n loops creates the situation of $A\ne 0$ when $\mathcal{E}=0$ and $B=0$, when the distance (d) from the solenoid $d^{″}{r}_0$. In this case A has only azimuthal component ( $A_{\theta }$ ) in the entire space from d distance. Inside the coil, we have, of course, the well-known $rot\left(B\right)=B_z=4\pi {\epsilon }_0{\mu }_{0}nI$.

The basic effects of the vector potential A in the quantum-mechanical processes indeed had been shown experimentally by the Aharonov-Bohm (AB) effect [26]. The A potential was directly verified pursuant to Equation (16). According to another experiment [27], the interference image shifts as compared to the free of the current case if the coil current is not equal to zero. The vector-potential A is a phase-shifter of the de Broglie-waves [28], measured experimentally too [29] Figure 1.

The minimal value of $A^2$ has physical meaning [30], measures the existence (change) of the topologic structures. It could be connected to a phase transition in quantum-chromodynamics too [31]. Despite the AB effect has a quantum (microscopic) nature, some AB observations are macroscopic presenting their theoretical and practical proofs.

The two potentials (A and $\phi$ ) determine the full field picture by simple mathematical transformations, so instead of the six variables (two vectors $\mathcal{E}$ and $\mathcal{H}$ ), only four parameters (A is a vector and $\phi$, is scalar) describes the complete electromagnetic phenomenon [32]. The potentials are not only auxiliary quantities, presented as the basis of the description of electromagnetism [32]. The conservation of electric charge in (3) and (14) was considered as a fundamental condition instead of the induction law (10). The potential Equation (18) was used [32]. In this approach, a variation principle derives from the above equations and the Maxwell theory. Interestingly the opposite process, from [32] from Maxwell equations, does not work. In the relativistic four-dimensional curved space-time the basis of the electrodynamic discussions is the four-dimensional potential vector, composed from the components of A and $\phi$ [33] [34].

Figure 1. Effect of vectorpotential on the electron’s eigenfunction, and the interference pattern. The shift is created by the presence of vectorpotential (Aharonov-Bohm effect).

3. Electromagnetic Forces

The fields are senseless for humans. A transformation to mechanical or high frequencies optical form must be involved to sense the electromagnetic activity. The optical frequencies present the fields in radiative waveforms, so presently, we deal with the force-transformation in invisible lower frequencies. Lorentz force density ( $f$ ) [35] connects the fields with the classical “force-based”, human mechanical sensing:

$f=\rho \mathcal{E}+j\times {\mu }_0\mathcal{H}$ (21)

In the existence of materials, when P and/or M are presented (this is the real case) ${\rho }_{eff}$ and $j_{eff}$ have to be applied in the Lorentz force:

$f={\rho }_{eff}\mathcal{E}+j_{eff}\times B$ (22)

The trivial force-free solution is when fields vanish. (See below the “field-free” solution.) The other, non-trivial vanish of the force is [36] when

$\rho {\mathcal{E}}^{″}j\times {\mu }_0\mathcal{H}$ and $j\left|\right|\mathcal{H}$ (23)

Formulate it with the polarization terms [37]:

$f=\rho \mathcal{E}+j\times B+\left(P\nabla \right)\mathcal{E}+\left(M\nabla \right)B+\left({\mu }_0\frac{\partial P}{\partial t}\times B\right)-\left({\mu }_0\frac{\partial M}{\partial t}\times \mathcal{E}\right)$ (24)

The complex force of (24) contains the direct forces, the dipole interactions ( $f_{dipole}$ ), and the radiation pressure ( $f_{rad}$ ) by two-two terms, respectively:

$f_{dipole}=\left(P\nabla \right)\mathcal{E}+\left(M\nabla \right)B$ (25)

$f_{rad}=\left({\mu }_0\frac{\partial P}{\partial t}\times B\right)-\left({\mu }_0\frac{\partial M}{\partial t}\times \mathcal{E}\right)$ (26)

These terms do not annihilate by (23) conditions. In consequence, the non-trivial solution of the force-field condition does not exist in bio-matter.

The potential formulation of the Lorentz force density by potentials (15) and (18) in the formulae (24):

$\begin{array}{c}f=-\rho \left(\frac{\partial A}{\partial t}+grad\left(\phi \right)\right)+j\times rot\left(A\right)-\left(P\nabla \right)\left(\frac{\partial A}{\partial t}+grad\left(\phi \right)\right)\\ +\left(M\nabla \right)rot\left(A\right)+\left({\mu }_0\frac{\partial P}{\partial t}\times rot\left(A\right)\right)+\left({\mu }_0\frac{\partial M}{\partial t}\times \left(\frac{\partial A}{\partial t}+grad\left(\phi \right)\right)\right)\end{array}$ (27)

The dynamics of charged particles could also be introduced in parallel of the classical dynamics an equation [38].

$\frac{\text{d}}{\text{d}t}\left(p_e+\frac{q}{c}A\right)=q\left(v\nabla \right)A+q\cdot v\times rotA-q\nabla \phi$ (28)

where $q$ is the electric charge. In more symmetric form:

$\frac{\text{d}}{\text{d}t}\left(p_e+\frac{q}{c}A\right)=-q\nabla \left(\phi -\frac{1}{c}\left(v\cdot A\right)\right)$ (29)

The Equation (29) shows important behaviors of the potentials: $eA$ is a momentum-like term, while ( $v\cdot A$ ) together with $\phi$ has potential character.

4. Tunneling through a Potential Barrier

There is no Lorentz force acting in the direction of the charge velocity, so no energy exchange could happen. The probability $p_i$ of an energy-state $E_i$ is proportional with the Boltzmann expression:

$p_i~{\text{e}}^{-\frac{E_i}{kT}}$ (30)

does not change by (curl-free) magnetic action in particle-description. In principle, we expect an effect of the curl-free field [39], on the basis of quantum mechanics.

The quantum-mechanics derives the surface and bulk chemical reactions governing the living processes. The Schrödinger picture of quantum mechanics in a case when a particle of charge q moves in the electromagnetic field can be described by the time-dependent single-particle equation with Ψ wave-function and 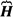Hamilton operator ignoring the reaction of a particle to the field:

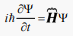(31)

The information obtainable about the system is given by the wave function Ψ normalized to one. Consequently, the phase of wave function includes all information relating to the system. It was shown by Aharonov and Bohm in their famous effect [40] that the potentials have a fundamental role in quantum-mechanics without using the electromagnetic fields. Schrödinger equation where $\Psi \left(r,t\right)$ is the complex wave function is a Hamilton operator, describing the total energy of the system, which, in the case of Aharonov-Bohm conditions [40], can be expressed as follows:

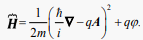(32)

where q is the charge in the V volume

$q={\displaystyle {\int }_V\rho \text{d}{r}^3}$ (33)

Consequently, the Schrödinger equation of (31):

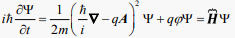(34)

In Equation (34) only the potentials have a role; the classical fields are completely missing. The scalar potential affects the potential energy, while the vector potential is connected to the charge’s momentum in the Schrodinger equation. In the plane-wave solution

$\Psi \left(r,t\right)\propto \exp \left(i\frac{E\cdot t-\left(p_m+qA\right)r}{h}\right)$ (35)

Note classical fields do not appear in Equation (34) too. Where $p_m$ is the mechanical momentum of the particle with m mass and $v$ speed:

$p_m=m\cdot v$ (36)

In consequence of (35), the magnetic vector-potential changes the wave-number only. Using the normality of Ψ

${\displaystyle {\int }_{V,\left|r\right|\to \infty }\Psi \left(r,t\right){\Psi }^{*}\left(r,t\right)\text{d}V}=1$ (37)

and using (35) the coordination dependence of Ψ is:

$\frac{1}{r}\exp \left(-\frac{p_{r}r}{h}\right)\exp \left(-i\frac{q{A}_{r}r}{h}\right)$ (38)

which changes the amplitude of the wave-function at the transmission of a potential-barrier (Figure 2). The amplitude of the probability could be higher and also less under the action of the vector potential than without it.

Consequently, when two charged particles create a chemical bond, the external vector-potential interacts and changes the structure.

The average of effective sources $j_{eff}$ and ${\rho }_{eff}$ could be expressed by:

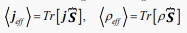(39)

where 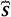is the Neumann’s density operator:

(40)

This approach (in principle) makes the complex system completely calculable.

5. The “Curl-Free” Potential Situation

A challenge arises when we have a curl-free magnetic vector potential:

$rot\left(A\right)=0$, (41)

In this case, (according to (15)) the Bfield vanishes, pure A field exists only [41]. A kind of the curl-free solution is free from the magnetic field, but according to (11) at high frequencies:

Figure 2. Particle transmission through a potential barrier with and without magnetic vector potential.

$rot\left(B\right)\approx 0$ (42)

because from (11) a part could be zero, and the other part near to zero:

${\mu }_{0}j+{\mu }_{0}rot\left(M\right)=0$ and ${\mu }_0{\epsilon }_0\frac{\partial \mathcal{E}}{\partial t}+{\mu }_0\frac{\partial P}{\partial t}\approx 0$ (43)

The electric field does not vanish if A changes by time ( $A=A\left(t\right)$ ):

$\mathcal{E}=-grad\left(\phi \right)-\frac{\partial A}{\partial t}\ne 0$ (44)

Of course, the curl-free solution could have bio-interactions having electric field and through this direct forces and energy absorption in the material. Using the potentials and the material parameters effective values of the sources ( ${\rho }_{eff}$ and $j_{eff}$ ) can be introduced by potentials alone in case of (41) conditions, too:

$j_{eff}=j+\frac{\partial P}{\partial t}+rot\left(M\right)=\frac{1}{{\mu }_0}\left(\Delta A-{\epsilon }_0{\mu }_0\frac{{\partial }^{2}A}{\partial t^2}\right)$ (45)

and

${\rho }_{eff}=\rho -{\epsilon }_{0}div\left(P\right)=-{\epsilon }_0\left(\Delta \phi -{\epsilon }_0{\mu }_0\frac{{\partial }^2\phi }{\partial t^2}\right)$ (46)

The time-dependent curl-free solution is a solution in the “pure” $\mathcal{E}$ -field, which is the most common in the literature, and mistakenly used as field free. The entire free field solution requests the following conditions:

$\frac{\partial A}{\partial t}=0$ and $grad\left(\phi \right)=const.$ (47)

Note due to (41) a $\chi$ scalar-potential could be introduced:

$A=-grad\left(\chi \right)$ (48)

and so

$\frac{\partial A}{\partial t}+grad\left(\phi \right)=grad\left(-\frac{\partial \chi }{\partial t}+\phi \right)=0$ (49)

Consequently, due to (18) the new scalar potential is time-dependent, as:

${\phi }^{\prime }\left(t\right)\Rightarrow \phi -\frac{\partial \chi }{\partial t}$ (50)

6. “Field-Free” Solution

The important question is the real field-free solution, when nor $\mathcal{E}$ nor B exist.

$B=rot\left(A\right)=0$ and $\mathcal{E}=-grad\left(\varphi \right)-\frac{\partial A}{\partial t}=0$ (51)

The field-free solution does not mean that the space is also potential free. Could it interact with the biomatter?

The field-free condition involves a full annihilation of the existing but identical and opposite fields. Due to the opposite ponderomotoric forces, the fields will vanish from the system. The zero B could be described by the two oppositely effective (destructive interference) vector potentials $A$ and $A^{\star }$ :

$B=rot\left(A-A^{\star }\right)=0$ (52)

In consequence, we could have a U scalar potential due to $rot\left(A\right)=0$ for the difference $A_0$

$A_0=\left(A-A^{\star }\right)=grad\left(U\right)$ (53)

Let us choose at the same time the scalar potential on the way that $\mathcal{E}$ has zero value as well:

$\mathcal{E}=-grad\left(\phi -{\phi }^{*}\right)-\frac{\partial \left(A-A^{\star }\right)}{\partial t}=0$ (54)

In this case, using (52) we define:

${\phi }_0=\left(\phi -{\phi }^{*}\right)=\frac{\partial U}{\partial t}$ (55)

Similarly to (20), the wave equations of these potentials belong to the field-free (source-free) conditions. In consequence of (45) and (46), the waves of null-potentials have zero effective charge- and current-densities

$\begin{array}{l}{j}_{eff}\left(A,\phi \right)+j_{eff}\left(-A^{\star },-{\phi }^{*}\right)=j_{eff}\left(A_0,{\phi }_0\right)=0\\ {\rho }_{eff}(A,\phi )+{\rho }_{eff}\left(-A^{\star },-{\phi }^{*}\right)={\rho }_{eff}\left(A_0,{\phi }_0\right)=0\end{array}$ (56)

The sum is zero in the macroscopic view. However, it does not automatically make terms vanish, the terms could be non-zero in a microscopic view! In this way, the potentials associated with null-fields appear as waves:

$\begin{array}{l}\Delta A_0-{\epsilon }_0{\mu }_0\frac{{\partial }^2{A}_0}{\partial t^2}={\mu }_0{j}_{eff}=0\\ \Delta {\phi }_0-{\epsilon }_0{\mu }_0\frac{{\partial }^2{\phi }_0}{\partial t^2}=-\frac{{\rho }_{eff}}{{\epsilon }_0}=0\end{array}$ (57)

There is a huge challenge: the waves of potentials in field-free solutions have no dumping. In consequence of the zero-field conditions, a U scalar potential in (53) and (55) is the potentials’ generator-function. Using (19), (52) and (54), a wave-equation is obtained for U:

$\Delta U-{\epsilon }_0{\mu }_0\frac{{\partial }^{2}U}{\partial t^2}=0$ (58)

The result in (58) supports the propagation of the scalar-wave (SW), which has no energy-dissipation in its transmission in the material [42]. The consequence of the SW concept, the Lorentz condition in (19) has been modified:

$divA+{\epsilon }_0{\mu }_0\frac{\partial \phi }{\partial t}=C$ (59)

where constant, and followingly [43]:

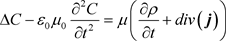(60)

Due to the charge conservation rule (3):

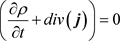(61)

Consequently:

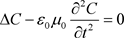(62)

Which is equal with (58).

Due to

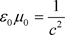(63)

These null-potential waves (together with the wave of the U potential (58)), are traveling by the speed of light in the vacuum (c), and so there are not dumping. [Note the limited velocity (c) of null-field potential obtained only with Lorencz condition (19).] Also, as we see from (16), the Ф flux obtained zero of course for field-free potentials for classical approach because

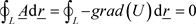(64)

The field-free potential in the Schrodinger equation is:

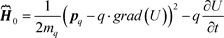(65)

The application of the Lorentz condition (19) is equal with the wave-equation condition (58) of the scale-transformation because the

(66)

transformations make identical results. Without damping the traveling waves, their interaction with the matter is questionable due to the missing energy loss. Is this challenge dissolvable?

7. The Stochastic Solution of the Field-Free Challenge

The mean’s zero value does not mean that all terms vanish in the sum. The sum of the terms is zero (time-averaged), but because of the non-linear P and M, the terms in sums in (56) could have non-zero values, keeping their sum zero. The effective current and charge densities as the fields’ sources could have fluctuation around zero in the field-free solutions, which is, in fact, a fluctuating field with zero outcomes. Consequently, the zero-field potential could affect the electrical and magnetic polarization pattern, or ohmic terms, in creep. Ponderomotoric forces do not connect to zero potential waves. The forces reorganize only the pattern of charges and currents, rearrange the structure without energy absorption. The fluctuations drive the structural changes of the patterns. This is a direct potential effect without any change of the actual energy state only rearranges its fluctuation distribution, which was shown on water-structure and in the water content of seeds too [44]. The vector potential affects the coupling matrixes of the transport equations and modifies the quantum-states of the water [45]. The water state changes show the clustering, and the experiments well agreed with the direction of the effect.

The spatio-temporal distribution of the fluctuations could vary without any change in the average (mean) values. Denote a living process without stochastic memory as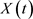. Its fluctuation by timedt:

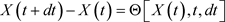(67)

The 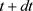time develops by its previous value at t time in (67). It is a Markovian process [46], determines the development in subsequent series of values. The 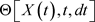function depends on the X,t,dt variables, and

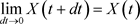. (68)

A self-similar process characterized [47] [48] by:

(69)

and in limit:

(70)

The terms are statistically independent representations in cases without memory. The sum of the n-pieces of the is normally distributed, [49] at large n according to thefunctional central limit theorem. Consequently, from (70):

(71)

where “mean” signifies the mean-value, m is the first, and σ is the second momentum of the distribution; and “var” denotes the standard deviation. The solutions of the function-Equation (71) are:

(72)

where A and D are smooth functions of X and t, as well as D is positive. With the normality conditions of (67) we get:

(73)

where is a normally distributed stochastic process with a mean and standard deviation and, respectively. (73) leads to a Langevin equation with an infinite standard deviation pumped by a normally distributed white noise (Γ(t)):

(74)

where:

(75)

A set of N self-similar stochastic processes could model the living system. Using the above considerations, we get a generalized Langevin equation:

(76)

Assuming the as a homogeneous linear function:

(77)

we get the comprehensive vectorial form of the generalized Langevin equation.

(78)

where X, D and are derived from, and, respectively. According to the Onsager’s conditions [50] the matrix is symmetrical, and the cross-effects are equal. The living matter forms a highly self-organized hierarchical structure, with a non-linear, dynamic equilibrium with no stationary processes [51]. Various physical, chemical, and physiological activities connect its subsystems, and interacting signals regulate and control a complex network. Even the simplest living biological systems show several interconnected processes on different time scales, determined by bioscaling connections [52]. Two identical living objects do not exist. The living matter is variable, changeable, mutable, and adaptable [53]. The living matter essentially differs from the lifeless ones [54]. While the thermal and quantum fluctuations in the lifeless states are negligible due to the system’s size. These lifeless materials do not change between identical environmental conditions. The living object has many randomly transformed and altered homologous phases and states interacting with each other, mutating over time, involving a permanent and immanent change that allows adaptation, mutation, and natural selection. This dynamism appears in the change of the confirmation state of proteins, optimizing life’s enzymatic reactions. Due to the inherent fluctuations, the living matter is “noisy”. The self-similar [55] and self-organized [56] behaviors drive the power-spectrum of their noise to a highly specialized frequency distribution, called pink-noise (1/f noise), [57] [58]. As we had shown earlier [59], the symmetrical, cyclical matrix mandatory for pink noise in a system. Consequently, if a stochastic process is self-similar, then generates pink-noise with a power density spectrum by f frequency:

(79)

This spectrum is independent of the kind and number of variables. The only assumption is its coupling matrix cyclically symmetric [59]. The living matter has such a matrix form, and its noises satisfy the (79) equation.

The vector-potential A is an axial vector (pseudovector), which at the reflection is opposite to its mirror image, without changing its magnitude, while the reflection of a true (polar) vector is exactly the same as its mirror image. The symmetry drastically changes by the effect of an axial vector, and Casimir’s anti-symmetric relation [60] replaces the Onsager’s symmetry:

(80)

in the indexed form:

(81)

This effect is the rearranging of the fluctuation-noise distribution by the changing of the coupling of interconnected processes. This effect is independent of the presence of fields, only the action of the vector-potential (A) is necessary. In a zero-field (“field-free”) case, the microscopic (quantum-level) A could vary freely, keeping the condition (56) valid in the macroscopic scale.

Resulting from our above calculation, the presence of any axial-vectors (e.g., magnetic field B or vector potential A) could destroy the symmetry of the -matrix [30]. Consequently, any axial-vector changes the coupling between the transport processes and effectively affects the noise-spectra and the interconnection of the various homologous phases of the actual living state. This special interaction behavior could give a clue to explain the certain respiration change by a magnetic field [61] or a proposed tumor-genesis theory by magnetic field interactions [62] [63]. The action of axial vectors on the bio-system could affect its self-organizing ability, directly affecting individual cellular organizing autonomy, which characterizes the cancer cells. The pink-noise fluctuation (and the connected large-scale maximal entropy) is broken by the axial vectors’ effect, modifying the transport properties and the interactions’ symmetry. This effect could modify the critical state and the correlation length of the interactions [64] and could create a stress-like effect on the organism.

8. The Bio-Entropy

We are able to formulate our results on the basis of thermodynamics as well. The highest deficiency of information (highest entropy) is achieved by the noise, which has Gaussian distribution [60] (Gaussian noise). Because the effective power-density of pink-noise is constant in all the characteristic scales, the Gaussian pink-noise then has maximal entropy in all the scales. The living system has special fractal dynamism, [65], in consequence of its self-similar stochastic behavior, it fluctuates by pink-noise, [59] [66]. The maximal entropy of Gaussian pink-noise allows an important conclusion: the living state’s noise has maximal entropy (stable dynamic equilibrium) in all of the characteristic scales. Applied the Focker-Plank equation [67] we had shown [30] that the entropy fluctuation is connected to the coefficients of the Langevin-equation too:

. (82)

In this case the elements of the cyclic -matrix will determine the change of the entropy. The applied field-free potential could change the configurational entropy and the noise-spectra of the living matter. This agrees well with the meaning of the minimum value of the volume integral of vector-potential squared (), which is connected to the topological structures of the matter [30].

Numerous negative feedback loops control the homeostasis [68] [69], creating both the micro and macro-structures in equilibrium. The control forms oppositely effective physiologic feedback signal-pairs (promoter-suppressor actions) in various time-scales. The system is well controlled at all times. The homeostasis fixes the system in regulated dynamic equilibrium.

To characterize the homeostatic equilibrium, we may introduce a special entropy-definition. There are various proposals to calculate the entropy of finite data-series, which are coherent with the Shannon-type entropy [70]. Measuring the complexity of time-series was introduced by the Richman-Moorman-entropy (S_E) [71], which is the negative logarithm of that conditional probability that the vectors remain r-neighbors when we add a new sample-point to the time-series so the length of the vectors is elongated to. Consequently:

(83)

The signals are kept in a definite interval, controlled on all scales of the homeostatic system. The entropy of every signal in this state is identical and constant;, independent of the scale of measurements, [72]. The controlling physiological signals fluctuate around their average values. The fluctuation is time-fractal (pink-noise), which characterizes homeostasis.

A special method, called multiscale entropy analysis (MSE) [73], has proved the scale-independency of pink-noise in a definite interval of the signals, proven by evaluation of various physiological signals [74]. Applying the MSE for pink- and white-noises and the entropy vs. the applied scale factors (number of the members of the actual averaging) had different functions. The smoothing (filtering, cutting the high-frequencies) is irrelevant in the case of the pink-noise. When the original was pink, the entropy remains constant on all scales in a very wide range of limits. The growing scale-factors decrease the white-noise entropy due to the very short correlation, but its entropy is high at the small scales due to the short-range correlations. While in the case of pink-noise, the short correlation is weak, but the long is strong.

9. Conclusions

Our present work shows the possible bio-effects of the electromagnetic potentials without the presence of electromagnetic fields. The effect is expected on the quantum level. It is based on the change of interactions of stochastic processes in living objects.

The practical benefit of the results is evident. It is not only a great possibility to work out new bio-effects, but it has industrial application possibilities also. The amplitude of field-free potential does not decrease because it does not induce Eddy current by the induction law to dissipate its energy. Consequently, effective communication methods can be achieved by applying low energies. Extensive research had been carried out in this field. An example, several patents were filed on behalf of Honeywell Inc., and granted on the communication system of this type [75].

Acknowledgements

This work was supported by the Hungarian National Research Development and Innovation Office PIACI KFI grant: 2019-1.1.1-PIACI-KFI-2019-00011.

Conflicts of Interest

The author declares no conflicts of interest regarding the publication of this paper.

References

[1]	Lei, H., Pan, Y., Wu, R. and Lv, Y. (2020) Innate Immune Regulation under Magnetic Fields with Possible Mechanisms and Therapeutic Applications. Frontiers in Immunology, 11, Article ID: 582772. https://doi.org/10.3389/fimmu.2020.582772
[2]	Zhu, M., Yang, Z., Yu, H., et al. (2020) The Efficacy and Safety of Low-Frequency Rotating Static Magnetic Field Therapy Combined with Chemotherapy on Advanced Lung Cancer Patients: A Randomized, Double Blinded, Controlled Clinical Trial. International Journal of Radiation Biology, 96, 943-950. https://doi.org/10.1080/09553002.2020.1748737
[3]	Diao, Y.L., Sun, W.N., He, Y.Q., et al. (2017) Equivalent Magnetic Vector Potential Model for Low-Frequency Magnetic Exposure Assessment. Physics in Medicine and Biology, 62, 7905-7922. https://doi.org/10.1088/1361-6560/aa8490
[4]	Lednev, V.V. (1991) Possible Mechanism for the Influence of Weak Magnetic Fields on Biological Systems. Bioelectromagnetics, 12, 71-75. https://doi.org/10.1002/bem.2250120202
[5]	Belyavskaya, N.A. (2004) Biological Effects Due to Weak Magnetic Field on Plants. Advances in Space Research, 34, 1566-1574. https://doi.org/10.1016/j.asr.2004.01.021
[6]	Tao, F.-M. (2003) Solvent Effects of Individual Water Molecules. In: Buch, V. and Devilin, J.P., Eds., Water in Confining Geometries, Cluster Physics, Springer Verlag, Berlin, 79-99. https://doi.org/10.1007/978-3-662-05231-0_5
[7]	Buchachenko, A. (2016) Why Magnetic and Electromagnetic Effects in Biology Are Irreproducible and Contradictory? Bioelectromagnetics, 37, 1-13. https://doi.org/10.1002/bem.21947
[8]	Smith, W. (2004) Quanta and Coherence Effects in Water and Living Systems. The Journal of Alternative and Complementary Medicine, 10, 69-78. https://doi.org/10.1089/107555304322848977
[9]	Eden, D. (2008) Energy Medicine. Little, Brown Book Group.
[10]	Rampl, I., Palko, L., Hyrsl, P. and Vojtek, L. (2012) Pulsed Vector Magnetic Potential Field Existence. World Journal of Condensed Matter Physics, 2, 202-207. https://doi.org/10.4236/wjcmp.2012.24034
[11]	Randerson, J. (2007) Electrosmog in the Clear with Scientists. The Guardian, January 18. https://www.theguardian.com/technology/2007/jan/18/guardianweeklytechnologysection4
[12]	Oschman, J. (2000) Energy Medicine. The Scientific Basis, Churchill Livingstone.
[13]	Jain, S. and Mills, P.J. (2010) Biofield Therapies: Helpful or Full of Hype? A Best Evidence Synthesis. International Journal of Behavioral Medicine, 17, 1-16.
[14]	Meyl, K. (2001) Scalar Waves: Theory and Experiments. Journal of Scientific Exploration, 15, 199-205. https://doi.org/10.1054/cuor.2001.0179
[15]	Tiller, W.A. (1999) Subtle Energies. Science & Medicine, 6, May/June.
[16]	Hall, H. (2005) A Review of Energy Medicine: The Scientific Basis. Skeptic Magazine, 11. http://quackfiles.blogspot.com/2006/01/review-of-energy-medicine-scientific.html
[17]	Bruhn, G.W. (2000) Commentary on the Chapter “Scalar Waves” in “Energy Medicine—The Scientific Basis”. http://www.mathematik.tu-darmstadt.de/~bruhn/Commentary-Oschman.htm
[18]	Bruhn, G.W. (2001) On the Existence of K. Meyl’s Scalar Waves. Journal of Scientific Exploration, 15, 206-210.
[19]	Hornberger, J. (2019) Who Is the Fake One Now? Questions of Quackery, Worldliness and Legitimacy. Critical Public Health, 29, 484-493. https://doi.org/10.1080/09581596.2019.1602719
[20]	Maclis, R.M. (1993) Magnetic Healing, Quackery, and the Debate about the Health Effects of Electromagnetic Fields. Annals of Internal Medicine, 118, 376-383. https://doi.org/10.7326/0003-4819-118-5-199303010-00009
[21]	Mckenzie, B. (2020) Do Pulsed Electromagnetic Field Devices Offer Any Benefit? Veterinary Practice News, Jan. 2 2020.
[22]	Basford, J.R. (2001) A Historical Perspective of the Popular Use of Electric and Magnetic Therapy. Archives of Physical Medicine and Rehabilitation, 82, 1261-1269. https://doi.org/10.1053/apmr.2001.25905
[23]	Barrett, S. (2008/2019) Magnet Therapy: A Skeptical View. Quackwatch. https://quackwatch.org/consumer-education/qa/magnet
[24]	Maxwell, J.C. (1998) A Treatise on Electricity and Magnetism. Clarendon Press, Oxford.
[25]	Lee, J.-H. and Chen, K.-M. (1982) Eddy Currents Induced by RF Magnetic Fields in Biological Bodies. Radio Science, 17, 61S-76S.
[26]	Pauli, W. (1958) Prinzipien Der Quantentheorie. Handbuch Der Physik bd. V. Springer Verlag, Berlin.
[27]	Marton, L. (1952) Electron Interferometer. Physical Review, 85, 1057-1058. https://doi.org/10.1103/PhysRev.85.1057
[28]	Konopinsky, E.J. (1978) What the Electromagnetic Vector Potential Describes. American Journal of Physics, 46, 499-502. https://doi.org/10.1119/1.11298
[29]	Chambers, R.G. (1960) Shift of an Electron Interference Pattern by Enclosed Magnetic Flux. Physical Review Letters, 5, 3-5. https://doi.org/10.1103/PhysRevLett.5.3
[30]	Gubarev, F.V., Sodolsky, L. and Zakharov, V.I. (2001) On the Significance of the Vector Potential Squared. Physical Review Letters, 86, 2220-2222. https://doi.org/10.1103/PhysRevLett.86.2220
[31]	Gubarrev, F.V. and Zakharov, V.I. (2000) On the Emerging Phenomenology of < (Aμa)min2   >. Physics Letters B, 501, 28-36. https://doi.org/10.1016/S0370-2693(01)00085-5
[32]	Mie, G. (1912) Grundlagen einer theorie der materie. Annalen der Physik, 37, 39, 40. https://doi.org/10.1002/andp.19123441102
[33]	Griffiths, D.J. (2007) Introduction to Electrodynamics. 3rd Edition, Pearson Education, Dorling Kindersley, London.
[34]	Cleani, F., Di Tommaso, A.O. and Vassallo, G. (2017) Maxwell’s Equations and Occam’s Razor. Journal of Condensed Matter Nuclear Science, 25, 100-128.
[35]	Simonyi, K. (1979) Theoretische Elektrotechnik. Vol. 20, 7th Edition, VEB Verlag, Berlin.
[36]	Vandas, M. and Romashets, E.P. (2003) A Force-Free Field with Constant Alpha in an Oblate Cylinder: A Generalization of the Lundquist Solution. Astronomy & Aastrophysics, 398, 801-807. https://doi.org/10.1051/0004-6361:20021691
[37]	Einstein, A. and Laub, J. (1908) über die im elektromagnetischen Felde auf ruhende Körper ausgeübten ponderomotorischen Kräfte [On the Ponderomotive Forces Exerted on Bodies at Rest in the Electromagnetic Field]. Annalen der Physik, 26, 541-550. (In German) https://doi.org/10.1002/andp.19083310807
[38]	Landau, L.D. and Lifsic, E.M. (1973) Theoretical Physics, II. Field Theory. Nauka Press, Moscow. (In Russian)
[39]	Rein, G. and Tiller, W.A. (1996) Anomalous Information Storage in Water: Spectroscopic Evidence for Non-Quantum Informational Transfer. Proceedings 3rd International Symposium on New Energy, Denver, 24-28 April 1996, 365.
[40]	Aharonov, Y. and Bohm, D. (1959) Significance of Electromagnetic Potentials in Quantum Theory. Physical Review, 115, 485-491. https://doi.org/10.1103/PhysRev.115.485
[41]	Szasz, A., Vincze, Gy., Andocs, G. and Szasz, O. (2009) Do Field-Free Electromagnetic Potentials Play a Role in Biology? Electromagnetic Biology and Medicine, 28, 135-147. https://doi.org/10.1080/15368370802711938
[42]	Reed, D. and Hively, L.M. (2020) Implications of Gauge-Free Extended Electrodynamics. Symmetry, 12, 2110. https://doi.org/10.3390/sym12122110
[43]	Reed, D. (2019) Unravelling the Potentials Puzzle and Corresponding Case for the Scalar Longitudinal Electrodynamic Wave. IOP Journal of Physics Conference Series, 1251, Article ID: 012043. https://doi.org/10.1088/1742-6596/1251/1/012043
[44]	Andocs, G., Vincze, Gy., Szasz, O., Szendro, P. and Szasz, A. (2009) Effect of Curl-Free Potentials on Water. I. Electromagnetic Biology and Medicine, 28, 166-181. https://doi.org/10.1080/15368370902724724
[45]	Tao, F.-M. (2003) Solvent Effects of Individual Water Molecules, In: Buch, V. and Devilin, J.P., Eds., Water in Confining Geometries, Cluster Physics, Springer Verlag, Berlin, 79-99. https://doi.org/10.1007/978-3-662-05231-0_5
[46]	Gagniuc, P.A. (2017) Markov Chains: From Theory to Implementation and Experimentation. John Wiley & Sons, Amsterdam, 1-235. https://doi.org/10.1002/9781119387596
[47]	Gillespie, D.T. (1992) Markov Processes. Academic Press, San Diego.
[48]	Gillespie, D.T. (1996) The Mathematics of Brown Motion and Johnson Noise. American Journal of Physics, 64, 225. https://doi.org/10.1119/1.18210
[49]	Vincze, I. (1971) Matematische Statistik mit Industriellen Anwendungen. Akadémiai Kiadó, Budapest.
[50]	Onsager, L. (1931) Reciprocal Relations in Irreversible Processes. Physical Review, 37, 405-426. https://doi.org/10.1103/PhysRev.37.405
[51]	Walleczek, J. (2000) Self-Organized Biological Dynamics & Nonlinear Control. Cambridge University Press, Cambridge. https://doi.org/10.1017/CBO9780511535338
[52]	Brown, J.H. and West, G.B. (2000) Scaling in Biology. Santa Fe Institute in the Sciences of Complexity, Oxford University Press, Oxford.
[53]	Musha, T. and Sawada, Y. (1994) Physics of the Living State. IOS Press, Amsterdam.
[54]	Marjan, M.I. and Szasz, A. (2000) Self-Organizing Processes in Non-Crystalline Materials: From Lifeless to Living Objects. OncoTherm Kft., Budapest.
[55]	West, G.B., Brown, J.H. and Enquist, B.J. (1999) The Four Dimension of Life: Fractal Geometry and Allometric Scaling of Organisms. Science, 284, 1677-1679. https://doi.org/10.1126/science.284.5420.1677
[56]	Camazine, S., Deneubourg, J.-L., Franks, N.R., Sneyd, J., Theraulaz, G. and Bonabeau, E. (2003) Self-Organization in Biological Systems, Princeton Studies in Complexity. Princeton University Press, Oxford.
[57]	West, B.J. (1990) Fractal Physiology and Chaos in Medicine. World Scientific, Singapore.
[58]	Bassingthwaighte, J.B., Leibovitch, L.S. and West, B.J. (1994) Fractal Physiology. Oxford University Press, New York. https://doi.org/10.1007/978-1-4614-7572-9
[59]	Szendro, P., Vincze, G. and Szasz, A. (2001) Pink Noise Behaviour of the Bio-Systems. European Biophysics Journal, 30, 227-231. https://doi.org/10.1007/s002490100143
[60]	Sharipov, F. (2006) Onsager-Casimir Reciprocal Relations Based on the Boltzmann Equation and Gas-Surface Interaction: Single Gas. Physical Review E, 73, Article ID: 026110. https://doi.org/10.1103/PhysRevE.73.026110
[61]	Reno, V.R. and Nutini, L.G. (1963) Effect of Magnetic Fields on Tissue Respiration. Nature, 198, 204-205. https://doi.org/10.1038/198204b0
[62]	Wolf, A.A. (1981) On a Unified Theory of Cancer Etiology and Treatment Based on the Superconduction Double-Dipole Model. Physiological Chemistry and Physics, 13, 493-510.
[63]	Easterly, C.E. (1981) Cancer Link to Magnetic Field Exposure: A Hypothesis. American Journal of Epidemiology, 114, 169-175. https://doi.org/10.1093/oxfordjournals.aje.a113179
[64]	Bak, P., Tang, Ch. and Wiesenfeld, K. (1987) Self-Organized Criticality: An Explanation of 1/f Noise. Physical Review Letters, 59, 381-384. https://doi.org/10.1103/PhysRevLett.59.381
[65]	Goldberger, A.L., Amaral, L.A.N., Hausdorff, J.M., Ivanov, P.Ch. and Peng, C.-K. (2001) Fractal Dynamics in Physiology: Alterations with Disease and Aging. PNAS Colloquium, 99, 2466-2472. https://doi.org/10.1073/pnas.012579499
[66]	Szendro, P., Vincze, Gy. and Szasz, A. (2001) Bio-Response to White Noise Excitation. Electro- and Magnetobiology, 20, 215-229. https://doi.org/10.1081/JBC-100104145
[67]	Haken, H. (1977) Synergetics. Springer-Verlag, Berlin. https://doi.org/10.1007/978-3-642-66784-8
[68]	Sneppen, K., Krisna, S. and Semsey, S. (2010) Simplified Models of Biological Networks. Annual Review of Biophysics, 39, 43-59. https://doi.org/10.1146/annurev.biophys.093008.131241
[69]	Turrigiano, G. (2007) Homeostatic Signaling: The Positive Side of Negative Feedback. Current Opinion in Neurobiology, 17, 318-324. https://doi.org/10.1016/j.conb.2007.04.004
[70]	Shannon, C.E. (1948) A Mathematical Theory of Communication. Bell System Technical Journal, 27, 379-423 and 623-656. https://doi.org/10.1002/j.1538-7305.1948.tb00917.x
[71]	Richman, J.S. and Moorman, J.R. (2000) Physiological Time-Series Analysis Using Approximate Entropy and Sample Entropy. American Journal of Physiology, 278, H2039-H2049. https://doi.org/10.1152/ajpheart.2000.278.6.H2039
[72]	Hegyi, G., Vincze, Gy. and Szasz, A. (2007) Axial Vector Interaction with Bio-Systems. Electromagnetic Biology and Medicine, 26, 107-118. https://doi.org/10.1080/15368370701380835
[73]	Costa, M., Goldberger, A.L. and Peng, C.K. (2005) Multiscale Entropy Analysis of Biological Signals. Physical Review E, 71, Article ID: 021906. https://doi.org/10.1103/PhysRevE.71.021906
[74]	Thuraisingham, R.A. and Gottwald, G.A. (2006) On Multiscale Entropy Analysis for Physiological Data. Physica A, 366, 323-332. https://doi.org/10.1016/j.physa.2005.10.008
[75]	Gelinas, R.C. (1984) United States Patent 4, 429, 280 (Jan. 31, 1984). https://doi.org/10.1093/nq/31-2-280