Power and Chebyshev Series Transformation Formulas with Applications to Solving Ordinary Differential Equations via the Fröbenius and Taylor’s Methods

Hippolyte Nyengeri, Rénovat Nizigiyimana, Jean-Pierre Mutankana, Henry Bayaga, Ferdinand Bayubahe

Department of Physics, Faculty of Science, University of Burundi, Bujumbura, Burundi.

DOI: 10.4236/oalib.1107142                

Abstract

In this paper, we present formulas that turn finite power series into series of shifted Chebyshev polynomials of the first kind. Thereafter, we derive formulas for coefficients of economized power series obtained by truncating the resulting Chebyshev series. To illustrate the utility of our formulas, we apply them to the solution of first order ordinary differential equations via Taylor methods and to solving the Schr?dinger equation (SE) for a spherically symmetric hyperbolic potential via the Fr?benius method. In each of the two applications, we show that the use of our formulas makes it possible to reduce the computing time, while preserving the accuracy of the results.

Keywords

Power Series, Chebyshev Polynomials, Economization, Taylor Methods, Fröbenius Method, Ordinary Differential Equations

1. Introduction

In this paper, we consider the formulas

${\displaystyle \underset{i=0}{\overset{N}{\sum }}}{a}_i{x}^i={\displaystyle \underset{i=0}{\overset{N}{\sum }}}{c}_i{T}_i^{*}\left(x\right)$ (1)

and

${\displaystyle \underset{i=0}{\overset{N-k}{\sum }}}{c}_i{T}_i^{*}\left(x\right)={\displaystyle \underset{i=0}{\overset{N-k}{\sum }}}{a}_i^{\left[k\right]}{x}^i$ (2)

where the $a_i$ coefficients in the truncated power series intervening in the left-hand side of Equation (1) are known, $N>2$, $\frac{N}{2}\le k<N$, the $c_i$ and $a_i^{\left[k\right]}$ coefficients are to be determined. The shifted Chebyshev polynomials $T_i^{\mathrm{<mo>\; *\; </mo>}}\left(x\right)$ are defined in the interval $\left[\mathrm{0,1}\right]$ by [1] [2].

$T_0^{*}\left(x\right)=1/2,T_n^{*}\left(x\right)=T_n\left(2x-1\right),n=1,2,3,\cdots ,$ (3)

where the first kind Chebyshev polynomials $T_n\left(x\right)$ are given by the recurrence relation

$T_{n+1}\left(x\right)=2x{T}_n\left(x\right)-T_{n-1}\left(x\right),n=1,2,3,\cdots ,$ (4)

with the starting values $T_0\left(x\right)=1$, $T_1\left(x\right)=x$.

Explicit expressions for the five first shifted Chebyshev polynomials are $T_0^{*}\left(x\right)=1/2$, $T_1^{*}\left(x\right)=2x-1$, $T_2^{*}\left(x\right)=8x^2-8x+1$, $T_3^{*}\left(x\right)=32x^3-48x^2+18x-1$, and $T_4^{*}\left(x\right)=128x^4-256x^3+160x^2-32x+1$.

The power of a variable x appeared originally purely in algebraic problems [3]. With the development of calculus, the great importance of power expansions became evident, notably in analytical treatment of differential equations via the so-called power series method and the Fröbenius method (FM) [3].

The power series method is one of the most powerful analytical methods that physicists have for solving linear differential equations. It gives solutions in the form of a power series expansion about any desired point $x=x_0,x$ being the independent variable. The FM generalizes the power series one. It gives solutions in the form of a power series multiplied by a logarithm term $\ln \left|x-x_0\right|$ or a fractional power ${\left(x-x_0\right)}^r$ [4]. It should be mentioned, however, that the power expansion suffers from slow convergence speed for points far from the origin of expansion. This means that for a desired level of accuracy, the points far from the origin will need substantially more terms than those close to the origin of expansion [5]. For computational purposes, however, it may be undesirable to require as many as N + 1 terms when N is large. Using series of orthogonal functions such as Chebyshev polynomials to approximate solutions of differential equations could alleviate the problem of slow convergence via the so-called economized power series.

We have to emphasize that the economization technique for power series using Chebyshev polynomials is based on the minimax property [6] [7] [8] [9] [10] according to which Chebyshev approximations are associated with the approximations which minimize the maximum error. The algorithm for this economization technique is lengthy because it has many distinct phases [11] [12] [13].

Consequently, it is for considerable interest to find formulas that turn truncated power series of the form ${\displaystyle {\sum }_{i=0}^N}{a}_i{x}^i$ into economized power series ${\displaystyle {\sum }_{i=0}^n}{e}_i{x}^i$ of a smaller degree n such that, in the range of interest, the absolute error introduced by the replacement of the original power series by the economized one is less than some acceptable value E [11]:

$\left|{\displaystyle \underset{j=0}{\overset{N}{\sum }}}{a}_j{x}^j-{\displaystyle \underset{j=0}{\overset{n}{\sum }}}{e}_j{x}^j\right|<E,x_0<x<x_1$ (5)

where $x_0=-1$ and $x_1=1$ when first kind Chebyshev polynomials are used in the economization procedure, $x_0=0$ and $x_1=1$ in the case of shifted Chebyshev polynomials of the first kind.

The main purpose of this paper is to find general formulas that directly transform any Nth-degree truncated power series defined in the interval $\left[\mathrm{0,1}\right]$ into an economized power series of a smaller degree n, using shifted Chebyshev polynomials of the first kind.

The rest of this paper is organized as follows. In Section 2, we establish formulas to transform any finite power series of a certain degree N into a series of first kind shifted Chebyshev polynomials and vice versa. Thereafter, we derive formulas for coefficients of truncated power series associated with the obtained Chebyshev series truncated to the $N-k+1$ first terms, where $N>2$ and $\frac{N}{2}<k<N$. In Section 3, we illustrate the utility of our formulas by means of two applications: first, we apply them to the solution of the Initial Value Problem (IVP) of the form

$y^{\prime }\left(t\right)\equiv \frac{\text{d}y}{\text{d}t}=f\left(t\mathrm{,}y\left(t\right)\right)\mathrm{,}a\le t\le b\mathrm{,}y\left(a\right)=y_a$ (6)

via Taylor methods [14] [15]; second, we apply our formulas to solving the Schrödinger equation (SE) for a spherically symmetric hyperbolic potential via the FM. In each of the two applications, we show that the use of our formulas makes it possible to reduce the computing time, while preserving the accuracy of the results. The conclusion is given in section 4.

2. Relations between Finite Power Series and Chebyshev Series

It is useful and convenient in various applications to be able to express power series explicitly in terms of power of Chebyshev polynomials, and vice versa. In this section, we concentrate on such expressions in the case of shifted Chebyshev polynomials of the first kind.

2.1. Finite Power Series in Terms of Series of First Kind Shifted Chebyshev Polynomials

We begin by relations between powers of x and shifted Chebyshev polynomials, which are useful to reduce the degree of a polynomial in the interval $\left[\mathrm{0,1}\right]$. We found it clarifying to use the formulas established by Ĺopez, Garcia and Caraveo [1]. These formulas can be summalized as [1] [16]

$\left[\begin{array}{c}\frac{1}{2}{\left(4x\right)}^0\\ \frac{1}{2}{\left(4x\right)}^1\\ \frac{1}{2}{\left(4x\right)}^2\\ ⋮\\ \frac{1}{2}{\left(4x\right)}^N\end{array}\right]=S\left[\begin{array}{c}{T}_0^{*}\left(x\right)\\ T_1^{*}\left(x\right)\\ T_2^{*}\left(x\right)\\ ⋮\\ T_N^{*}\left(x\right)\end{array}\right]$ (7)

and

$\left[\begin{array}{c}{T}_0^{*}\left(x\right)\\ T_1^{*}\left(x\right)\\ T_2^{*}\left(x\right)\\ ⋮\\ T_N^{*}\left(x\right)\end{array}\right]=P\left[\begin{array}{c}\frac{1}{2}{\left(4x\right)}^0\\ \frac{1}{2}{\left(4x\right)}^1\\ \frac{1}{2}{\left(4x\right)}^2\\ ⋮\\ \frac{1}{2}{\left(4x\right)}^N\end{array}\right]$ (8)

where:

・ $T_0^{*}\left(x\right)=\frac{1}{2}$ and thus $x^0=2T_0^{*}(\; x\; )$

・ $S={\left[S_{ij}\right]}_{i,j=0}^N$ is a $\left(N+1\right)\times \left(N+1\right)$ lower triangular matrix such that [1]

$S_{ii}=1,i=0,1,2,\cdots ,N,S_{ij}=0,j>i,$ (9)

$\begin{array}{l}{S}_{i0}=2\left(S_{i-1,0}+S_{i-1,1}\right)\\ S_{ij}=S_{i-1,j-1}+2S_{i-1,j}+S_{i-1,j+1}\end{array}\}i,j=1,\cdots ,N-1$ (10)

$S_{N0}=2\left(S_{N-1,0}+S_{N-1,1}\right),S_{Nj}=S_{N-1,j-1}+2S_{N-1,j}+S_{N-1,j+1},\mathrm{<mtext>\; \hspace{0.17em}\; </mtext>}j\in \left[1,N-1\right]$ (11)

$P=S^{-1}$ (12)

Since S is a lower triangular matrix with ones on the main diagonal, elements of the matrix P defined by Equation (12) can be computed recursively from [17]

$P_{jj}=1,P_{ij}=-{\displaystyle \underset{k=j}{\overset{i-1}{\sum }}}{S}_{ik}{P}_{kj},i=j+1,\cdots ,N$ (13)

From Equations (7) and (8), we obtain―after expressing the first four powers of x (resp. the first four $T_i^{\star }\left(x\right)$ polynomials) in terms of $T_i^{\star }\left(x\right)$ polynomials (resp. in terms of powers of x), and then generalizing the resulting formulas―the two following expressions:

$x^i=\frac{2}{4^i}{\displaystyle \underset{j=0}{\overset{i}{\sum }}}{S}_{ij}{T}_j^{*}\left(x\right),i=0,1,2,\cdots ,N$ (14)

and

$T_i^{*}\left(x\right)=\frac{1}{2}{\displaystyle \underset{j=0}{\overset{i}{\sum }}}{P}_{ij}{4}^j{x}^j,i=0,1,2,\cdots ,N.$ (15)

Non-vanishing elements of the first nine lines of matrices S and P are given in the two following equations:

$S=\left[\begin{array}{cccccccccc}1& & & & & & & & & \\ 2& 1& & & & & & & & \\ 6& 4& 1& & & & & & & \\ 20& 15& 6& 1& & & & & & \\ 70& 56& 28& 8& 1& & & & & \\ 252& 210& 120& 45& 10& 1& & & & \\ 924& 792& 495& 220& 66& 12& 1& & & \\ 3432& 3003& 2002& 1001& 364& 91& 14& 1& & \\ 12870& 11440& 8008& 4368& 1820& 560& 120& 16& 1& \\ ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& \ddots \end{array}\right]$ (16)

and

$P=\left[\begin{array}{cccccccccc}1& & & & & & & & & \\ -2& 1& & & & & & & & \\ 2& -4& 1& & & & & & & \\ -2& 9& -6& 1& & & & & & \\ 2& -16& 20& -8& 1& & & & & \\ -2& 25& -50& 35& -10& 1& & & & \\ 2& -36& 105& -112& 54& -12& 1& & & \\ -2& 49& -196& 294& -210& 77& -14& 1& & \\ 2& -64& 336& -672& 660& -352& 104& -16& 1& \\ ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& \ddots \end{array}\right]$ (17)

It can be easily verified that

$S_{i,i-1}=2i=-P_{i,i-1},i=1,2,\cdots ,N;$ (18)

$S_{i,i-2}=i^2+i\left(i-1\right);P_{i,i-2}=i^2+i\left(i-3\right),i=2,3,\cdots ,N.$ (19)

In order to transform the finite power series ${\displaystyle {\sum }_{i=0}^N}{a}_i{x}^i$ into the Chebyshev series of the form ${\displaystyle {\sum }_{i=0}^N}{c}_i{T}_i^{*}$, we first replace each power of x by its expression in terms of first kind Chebyshev polynomials, using relations given in Equation (14). Then we collect all the coefficients with the same Chebyshev polynomial $T_i^{*}\left(x\right);\mathrm{<mtext>\; \hspace{0.17em}\; </mtext>}i=0,1,2,\cdots ,N$. We find, after some manipulations, that

${\displaystyle \underset{i=0}{\overset{N}{\sum }}}{a}_i{x}^i={\displaystyle \underset{i=0}{\overset{N}{\sum }}}{c}_i{T}_i^{*}(\; x\; )$

with

$c_i=2{\displaystyle \underset{j=i}{\overset{N}{\sum }}}\frac{S_{ji}}{4^j}{a}_j,i=0,1,2,\cdots ,N.$ (20)

2.2. Finite Chebyshev Series in Terms of Power Series

We consider here the problem of transforming the finite Chebyshev series ${\displaystyle {\sum }_{i=0}^N}{c}_i{T}_i^{*}\left(x\right)$ into a finite power series of the same degree, i.e., ${\displaystyle {\sum }_{i=0}^N}{a}_i{x}^i$ To solve this problem, we begin by expressing each polynomial $T_i^{*}\left(x\right),\mathrm{<mtext>\; \hspace{0.17em}\; </mtext>}i=0,1,\cdots ,N$, in terms of powers of x, using relations given in Equation (15). Thereafter, we collect all the coeffcients with the same power of x. We obtain the following expression not found explicitely in the literature to the best of our knowledge.

$a_i=\frac{4^i}{2}{\displaystyle \underset{j=i}{\overset{N}{\sum }}}{P}_{ji}{c}_j,i=0,1,2,\cdots ,N.$ (21)

2.3. Useful Formulas for Economization of Power Series on the Interval [0, 1]

As stated earlier, the economization algorithm is lengthy because it has many distinct phases. More precisely, the economization of a power series, such as ${\displaystyle {\sum }_{i=0}^{\infty }}{a}_i{x}^i$ has four basic steps which are as follows when the economization is based on the use of shifted Chebyshev polynomials of the first kind:

Step 1 Truncate the given power series to obtain a polynomial

$P_N\left(x\right)=a_0+a_{1}x+\cdots +a_N{x}^N$ (22)

of degree N.

Step 2 Expand $P_N\left(x\right)$ in a Chebyshev series as follows:

$P_N\left(x\right)=c_0{T}_0^{*}\left(x\right)+c_1{T}_1^{*}\left(x\right)+\cdots +c_N{T}_N^{*}\left(x\right)$ (23)

making use of relations given in Equation (14).

Step 3 Truncate this Chebyshev series to a smaller number of terms by retaining the first n terms, choosing n so that the maximum error given by

$\left|P_N\left(x\right)-M_n\left(x\right)\right|\le E+\left|c_{n+1}\right|+\cdots +\left|c_N\right|$ (24)

is acceptable, where $M_n\left(x\right)$ designs the resulting small Chebyshev series, i.e.,

$M_n\left(x\right)=c_0{T}_0^{\mathrm{<mo>\; *\; </mo>}}\left(x\right)+c_1{T}_1^{\mathrm{<mo>\; *\; </mo>}}\left(x\right)+\cdots +c_n{T}_n^{\mathrm{<mo>\; *\; </mo>}}\left(x\right)\mathrm{,}$ (25)

whereas E represents the absolute error introduced by the replacement of $P_N\left(x\right)$ with $M_n\left(x\right)$.

Step 4 Replace $T_j^{\mathrm{<mo>\; *\; </mo>}}\left(x\right)\left(j=\mathrm{0,1,}\cdots \mathrm{,}n\right)$ by its polynomial form, which leads to

$P_N\left(x\right)\approx e_0+e_{1}x+\cdots +e_n{x}^n\mathrm{,}$ (26)

using Equation (15).

If necessary in step 1, i.e., when we have an interval $\left[a\mathrm{,}b\right]$ other than $\left[\mathrm{0,1}\right]$, make a transformation of independent variables so that the economization is valid on that interval, by means of the expression

$y=\frac{x-a}{b-a}$ (27)

In this case, it is necessary to change variable back to x after step 4, which makes the computing time more considerable.

To reduce the duration of the economization procedure, it is convenient to have a general formula for the coefficients $a_i^{\left[k\right]}\mathrm{,}i=\mathrm{0,1,2,}\cdots \mathrm{,}N-k$, defined by

${\displaystyle \underset{i=0}{\overset{N-k}{\sum }}}{c}_i{T}_i^{*}\left(x\right)={\displaystyle \underset{i=0}{\overset{N-k}{\sum }}}{a}_i^{\left[k\right]}{x}^i,1<k<N$ (28)

where the superscript [k] means that the finite power series of degree $N-k$ whose the $a_i^{\left[k\right]}$ are coefficients is just the Chebyshev form of $P_N\left(x\right)$ (see equations (23)), truncated to the first $N-k+1$ terms, i.e., the last k terms of the right hand side of Equation (23) are neglected.

In the rest of this section, we concentrate on establishing a general formula for the $a_i^{\left[k\right]}$ coefficients. For this purpose, we first derive expressions for the $a_i^{\left[1\right]}$, $a_i^{\left[2\right]}$ and $a_i^{\left[3\right]}$ coefficients successively, in terms of the $a_i$ coefficients, i.e., coefficients of the original Nth-degree truncated power series to be economized. Thereafter, we generalize these expressions to establish a formula for $a_i^{\left[k\right]}$, $i=0,1,\cdots ,N-k$ ; $1<k<N$.

2.3.1. Case When Only the Last Term Is Neglected

We start with the expression (1), where the $a_i$ coefficients are known and the $c_i$ coefficients are given by Equation (20). From Equation (1), we have

${\displaystyle \underset{i=0}{\overset{N-1}{\sum }}}{c}_i{T}_i^{*}\left(x\right)+c_N{T}_N^{*}\left(x\right)={\displaystyle \underset{i=0}{\overset{N-1}{\sum }}}{a}_i{x}^i+a_N{x}^N$ (29)

where

$c_N=2\frac{S_{NN}}{4^N}{a}_N=\frac{2}{4^N}{a}_N$ (30)

according to Equation (20) and to the fact that $S_{NN}=1$. Using Equation (15), we obtain

$T_N^{*}\left(x\right)=\frac{1}{2}{\displaystyle \underset{j=0}{\overset{N-1}{\sum }}}{P}_{Nj}{4}^j{x}^j.$ (31)

Combining equations (29), (30) and (31), we have:

${\displaystyle \underset{i=0}{\overset{N-1}{\sum }}}{c}_i{T}_i^{*}\left(x\right)={\displaystyle \underset{i=0}{\overset{N-1}{\sum }}}{a}_i{x}^i+a_N{x}^N-\frac{a_N}{4^N}{P}_{NN}{4}^N{x}^N-\frac{a_N}{4^N}{\displaystyle \underset{j=0}{\overset{N-1}{\sum }}}{P}_{Nj}{4}^j{x}^j$ (32)

$={\displaystyle \underset{i=0}{\overset{N-1}{\sum }}}{a}_i{x}^i-\frac{a_N}{4^N}{\displaystyle \underset{j=0}{\overset{N-1}{\sum }}}{P}_{Nj}{4}^j{x}^j$ (33)

since $P_{NN}=1$. This can be rewritten as

${\displaystyle \underset{i=0}{\overset{N-1}{\sum }}}{c}_i{T}_i^{*}\left(x\right)={\displaystyle \underset{i=0}{\overset{N-1}{\sum }}}{a}_i^{\left[1\right]}{x}^i$ (34)

where

$a_i^{\left[1\right]}=a_i-\frac{P_{Ni}{4}^i}{4^N}{a}_N,i=0,1,2,\cdots ,N-1.$ (35)

2.3.2. Case When the Last Two Terms Are Neglected

From Equation (34), we have

${\displaystyle \underset{i=0}{\overset{N-2}{\sum }}}{c}_i{T}_i^{*}\left(x\right)+c_{N-1}{T}_{N-1}^{*}\left(x\right)={\displaystyle \underset{i=0}{\overset{N-2}{\sum }}}{a}_i^{\left[1\right]}{x}^i+a_{N-1}^{\left[1\right]}{x}^{N-1}$ (36)

where

$c_{N-1}=2{\displaystyle \underset{j=N-1}{\overset{N}{\sum }}}\frac{S_{j,N-1}}{4^j}{a}_j=2\left(\frac{S_{N-1,N-1}}{4^{N-1}}{a}_{N-1}+\frac{S_{N,N-1}}{4^N}{a}_N\right)$ (37)

and

$T_{N-1}^{*}\left(x\right)=\frac{1}{2}\left[{\displaystyle \underset{j=0}{\overset{N-2}{\sum }}}{P}_{N-1,j}{4}^j{x}^j+P_{N-1,N-1}{4}^{N-1}{x}^{N-1}\right].$ (38)

Combination of Equations (36), (37) and (38) yields

$\begin{array}{c}{\displaystyle \underset{i=0}{\overset{N-2}{\sum }}}{c}_i{T}_i^{*}\left(x\right)={\displaystyle \underset{i=0}{\overset{N-2}{\sum }}}{a}_i^{\left[1\right]}{x}^i+a_{N-1}^{\left[1\right]}{x}^{N-1}-\left(\frac{S_{N-1,N-1}}{4^{N-1}}{a}_{N-1}+\frac{S_{N,N-1}}{4^N}{a}_N\right)\\ \times P_{N-1,N-1}{4}^{N-1}{x}^{N-1}-\left(\frac{S_{N-1,N-1}}{4^{N-1}}{a}_{N-1}+\frac{S_{N,N-1}}{4^N}{a}_N\right){\displaystyle \underset{j=0}{\overset{N-2}{\sum }}}{P}_{N-1,j}{4}^j{x}^j.\end{array}$ (39)

Collecting all coefficients of $x^{N-1}$ and taking into account Equation (18) and the expression of $a_{N-1}^{\left[1\right]}$ derived from (35), i.e.,

$a_{N-1}^{\left[1\right]}=a_{N-1}-\frac{P_{N,N-1}{4}^{N-1}}{4^N}{a}_N,$ (40)

we find that the term of degree $N-1$ in Equation (39) vanishes. Therefore, this equation can be rewritten as

${\displaystyle \underset{i=0}{\overset{N-2}{\sum }}}{c}_i{T}_i^{*}\left(x\right)={\displaystyle \underset{i=0}{\overset{N-2}{\sum }}}{a}_i^{\left[2\right]}{x}^i$ (41)

with

$a_i^{\left[2\right]}=a_i-\frac{P_{N-1,i}{4}^i}{4^{N-1}}{a}_{N-1}-\left[S_{N,N-1}\frac{P_{N-1,i}{4}^i}{4^N}+S_{NN}\frac{P_{Ni}{4}^i}{4^N}\right]a_N.$ (42)

2.3.3. Case When the Last Three Terms Are Neglected

In this case, we start with Equation (42) which can be rewritten as follows:

${\displaystyle \underset{i=0}{\overset{N-3}{\sum }}}{c}_i{T}_i^{*}\left(x\right)+c_{N-2}{T}_{N-2}^{*}\left(x\right)={\displaystyle \underset{i=0}{\overset{N-3}{\sum }}}{a}_i^{\left[2\right]}{x}^i+a_{N-2}^{\left[2\right]}{x}^{N-2}$ (43)

where

$c_{N-2}=2{\displaystyle \underset{j=N-2}{\overset{N}{\sum }}}\frac{S_{j,N-2}}{4^j}{a}_j$ (44)

and

$T_{N-2}^{*}\left(x\right)=\frac{1}{2}{\displaystyle \underset{j=0}{\overset{N-2}{\sum }}}{P}_{N-2,j}{4}^j{x}^j.$ (45)

Inserting the last two expressions into Equation (43), we get:

$\begin{array}{c}{\displaystyle \underset{i=0}{\overset{N-3}{\sum }}}{c}_i{T}_i^{*}\left(x\right)={\displaystyle \underset{i=0}{\overset{N-3}{\sum }}}{a}_i^{\left[2\right]}{x}^i+a_{N-2}^{\left[2\right]}{x}^{N-2}-[\frac{S_{N-2,N-2}}{4^{N-2}}{a}_{N-2}+\frac{S_{N-1,N-2}}{4^{N-1}}{a}_{N-1}\\ +\frac{S_{N,N-2}}{4^N}{a}_N]\left[{\displaystyle \underset{j=0}{\overset{N-3}{\sum }}}{P}_{N-2,j}{4}^j{x}^j+P_{N-2,N-2}{4}^{N-2}{x}^{N-2}\right]\end{array}$ (46)

The term of degree $N-2$ vanishes. This can be shown by inserting in the above equation expressions of $S_{N-\mathrm{2,}N-2}$ ; $S_{N-\mathrm{1,}N-2}$ ; $S_{N\mathrm{,}N-2}$ and $a_{N-2}^{\left[2\right]}$ obtained from Equations (9), (18), (19) and (42) respectively, not forgetting to replace the two matrix elements $P_{N-\mathrm{1,}N-2}$ and $P_{N\mathrm{,}N-2}$ intervening in $a_{N-2}^{\left[2\right]}$ with their expressions derived from (18) and (19). Therefore, Equation (46) becomes

${\displaystyle \underset{i=0}{\overset{N-3}{\sum }}}{c}_i{T}_i^{*}\left(x\right)={\displaystyle \underset{i=0}{\overset{N-3}{\sum }}}{a}_i^{\left[3\right]}{x}^i$ (47)

where

$\begin{array}{l}{a}_i^{\left[3\right]}=a_i-\frac{P_{N-2,i}{4}^i}{4^{N-2}}{a}_{N-2}-\frac{P_{N-1,i}{4}^i+S_{N-1,N-2}{P}_{N-2,i}{4}^i}{4^{N-1}}{a}_{N-1}\\ -\frac{S_{N,N-2}{P}_{N-2,i}{4}^i+S_{N,N-1}{P}_{N-1,i}{4}^i+P_{Ni}{4}^i}{4^N}{a}_N,i=0,\cdots ,N-3.\end{array}$ (48)

2.3.4. Generalization

A careful analysis of Equations (35), (42) and (48) suggests the following general formula for the $a_i^{\left[k\right]}$ coefficients:

$a_i^{\left[k\right]}=a_i-{\displaystyle \underset{j=1}{\overset{k}{\sum }}}{b}_{ji}{a}_{N-k+j},i=0,1,\cdots ,N\text{-}k$ (49)

where

$b_{ji}=4^i{\displaystyle \underset{q=0}{\overset{j-1}{\sum }}}\frac{S_{N-k+j,N-k+j-q}{P}_{N-k+j-q,i}}{4^{N-k+j}}$ (50)

To the best of our knowledge, this formula has not yet been reported in the literature.

For $k=4$, Equations (49) and (50) yield

$\begin{array}{c}{a}_i^{\left[4\right]}=a_i-4^i\left(\frac{P_{N-3,i}}{4^{N-3}}{a}_{N-3}-\frac{S_{N-2,N-3}{P}_{N-3,i}+P_{N-2,i}}{4^{N-2}}{a}_{N-2}\right)\\ -4^i\left(\frac{S_{N-1,N-3}{P}_{N-3,i}+S_{N-1,N-2}{P}_{N-2,i}+P_{N-1,i}}{4^{N-1}}{a}_{N-1}\right)\\ -4^i\left(\frac{S_{N,N-3}{P}_{N-3,i}+S_{N,N-2}{P}_{N-2,i}+S_{N,N-1}{P}_{N-1,i}+P_{Ni}}{4^N}{a}_N\right).\end{array}$ (51)

3. Applications

To illustrate the utility of our formulas, we apply them to two problems via two distinct methods:

・ The Initial Value Problem (IVP) of the form

$y^{\prime }\left(t\right)=\frac{\text{d}y}{\text{d}t}=f\left(t,y\left(t\right)\right),a\le t\le b,y\left(a\right)=y_a$ (52)

via the Taylor method of a certain order,

・ the Boundary Value Problem (BVP) constituted by the SE for a spherically symmetric hyperbolic potential given by [18]

$\begin{array}{l}V\left(r\right)=C_{-2}{\coth }^2\left(\alpha r\right)+C_{-1}\coth \left(\alpha r\right)+{\displaystyle \underset{i=1}{\overset{3}{\sum }}}{C}_i{\tanh }^i\left(\alpha r\right)\\ +{\displaystyle \underset{j=1}{\overset{K}{\sum }}}{B}_j{\text{sech}}^{2j}\left(\alpha r\right),r\in \left]0,+\infty \right[\end{array}$ (53)

and the boundary conditions $\psi \left(0\right)=0$ and $\psi \left(\infty \right)=0$, the method to be used being the FM.

3.1. Application to Taylor Methods for Initial Value Problems

We here consider the IVP of type (52) that possesses a unique solution on some specified interval. The object of Taylor methods is, in this situation, to obtain approximations to the solution of the IVP in question at N particular equally spaced points

$t_j=a+jh,j\in \left[1,N\right],N=\lfloor \frac{b-a}{h}\rfloor ,t_0=a,$ (54)

approximations to the numbers $y\left(t_1\right),y\left(t_2\right),\cdots ,y\left(t_N\right)$, rather than to the curve of $y\left(t\right)$. Taylor method of order n is, in the case of the IVP (52), defined by [14] [15]

$w_0=y_a,w_{i+1}=w_i+h{T}^{\left(n\right)}\left(t_i,w_i,h\right),i=0,1,\cdots ,N-1$ (55)

where

$T^{\left(n\right)}\left(t_i,w_i,h\right)=f\left(t_i,w_i\right)+\frac{h}{2}{f}^{\prime }\left(t_i,w_i\right)+\cdots +\frac{h^{n-1}}{n！}{f}^{\left(n-1\right)}\left(t_i,w_i\right),$ (56)

$w_i$ being the approximation of $y_i\equiv y\left(t_i\right)$. It is remarquable that Taylor methods are explicit and that the explicit Euler’s method is Taylor’s method of order one. Note that Equation (55) becomes

$w_0=y_a,w_{i+1}=w_i+{\displaystyle \underset{j=1}{\overset{n}{\sum }}}\frac{f^{\left(n-1\right)}}{n!}\left(t_i,w_i\right)h^n$ (57)

if $T^{\left(n\right)}\left(t_i\mathrm{,}{w}_i\mathrm{,}h\right)$ is replaced by its expression given by Equation (56).

The existence of the truncated power series of h in Equation (57) immediately suggests that the economization process can be used to improve the accuracy and speed of Taylor’s methods.

Table 1 contains the results produced by a fortran 90 code used to approximate the solution of the IVP given by

$y^{\prime }\left(t\right)=y-t^2+1,y\left(0\right)=0.5$ (58)

using Taylor methods of orders 14 and 20 with two different step sizes, i.e., $h=0.2$ and $h=0.9$. The exact solution, which is [15]

$y\left(t\right)={\left(t+1\right)}^2-0.5{\text{e}}^t$ (59)

is given in colunn 3, global errors for the fourteenth- and twentieth-orders Taylor methods in colunns 4 and 5 respectively.

It is obvious that the accuracy of Taylor’s methods decreases with h and increases with the order of the method.

In Table 2, we show results obtained after applying the economization process to the twentieth-order Taylor method for the IVP (58). We consider the fourteenth-degree economized power series only.

Table 1. Results for IVP (58) using Taylor’s methods of orders 14 and 20 with step sizes 0.2 and 0.9.

Table 2. Results for IVP (58) after applying the economization process to Taylor’s method of order 20 with k = 6 and step sizes 0.2 and 0.9.

Comparing Table 1 and Table 2, we see that w and y in Table 1 are not so close as in Table 2 for the step size $h=0.9$.

3.2. Application to One-Particule Radial Schrödinger Equation via the Fröbenius Method

The time-independent SE for a particule of mass M that moves in three dimemsional space under the effect of a spherically symmetric potential is given by

$-\frac{{\hslash }^2}{2M}\left[{\Delta }_r+V\left(r\right)\right]\text{ψ}\left(\stackrel{\to }{r}\right)=E\text{ψ}\left(\stackrel{\to }{r}\right)$ (60)

Taking $\text{ψ}\left(\stackrel{\to }{r}\right)=r^{-1}\psi \left(r\right)Y_{\mathcal{l}m}\left(\theta \mathrm{,}\phi \right)$ and considering potential (53), it is found that $\psi \left(r\right)$ must satisfy the radial SE

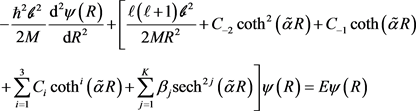(61)

where

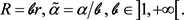(62)

To reduce Equation (61) into a differential equation solvable by means of the FM, we appeal to the following approximation for the centrifugal term $1/R^2$ [19]

$\frac{1}{R^2}\approx {\tilde{\alpha }}^2\left[\frac{s}{{\sinh }^2\left(\tilde{\alpha }R\right)}+\frac{t}{{\cosh }^2\left(\tilde{\alpha }R\right)}\right]$ (63)

where $\tilde{\alpha }$, $s$ and $t$ are adjustable dimensionless parameters. Substituting this approximation into (61) and making the change of variable $\xi =-\tanh \left(\tilde{\alpha }R\right)$, such that the domain $0<r<\infty$ maps to $-1<\xi <0$, we find:

$\begin{array}{l}{\xi }^2\left({\xi }^2-1\right)\frac{{\text{d}}^2\psi }{\text{d}{\xi }^2}+2{\xi }^3\left({\xi }^2-1\right)\frac{\text{d}\psi }{\text{d}\xi }+\frac{2M}{{\hslash }^2{\alpha }^2}[-\left(C_{-2}+\frac{\mathcal{l}\left(\mathcal{l}+1\right){\alpha }^{2}s}{2M}\right)+C_{-1}\xi \\ +\left(E+\frac{\mathcal{l}\left(\mathcal{l}+1\right){\alpha }^{2}s}{2M}\right){\xi }^2+C_1{\xi }^3-C_2{\xi }^4+C_3{\xi }^5-{\displaystyle \underset{j=1}{\overset{K}{\sum }}}{\tilde{B}}_j{\left(1-{\xi }^2\right)}^j{\xi }^2]\psi \left(\xi \right)=0\end{array}$ (64)

where the ${\tilde{B}}_j$ coefficients are such that

${\tilde{B}}_1=\frac{\mathcal{l}\left(\mathcal{l}+1\right){\alpha }^{2}t}{2M}+B_1,{\tilde{B}}_i=B_i,i=2,3,\cdots ,K.$ (65)

If we make the substitution $\eta =\xi +1$ in Equation (64), such that the domain $-1<\xi <0$ maps to $0<\eta <1$, and then apply the FM to the resulting differential equation by writing

$\psi \left(\eta \right)={\eta }^{\delta }{\displaystyle \underset{n=0}{\overset{\infty }{\sum }}}{a}_n{\eta }^n,$ (66)

we find that the recursion relation between successive coefficients is:

$\begin{array}{l}\left[4+d_0+\epsilon +4\delta \left(2+\delta \right)+8n\left(1+\delta \right)+4n^2\right]a_{n+1}\\ +\left[d_1-2\epsilon -2\delta \left(1+6\delta \right)-2n\left(1+12\delta \right)-12n^2\right]a_n\\ +\left[8+d_2+\epsilon -\delta \left(21-13\delta \right)-n\left(21-26\delta \right)+13n^2\right]a_{n-1}\\ +\left[-16+d_3+2\delta \left(10-3\delta \right)+4n\left(5-3\delta \right)-6n^2\right]a_{n-2}\\ +\left[6+d_4-\delta \left(5-\delta \right)-n\left(5-2\delta \right)+n^2\right]a_{n-3}+d_5{a}_{n-4}+{\displaystyle \underset{p=6}{\overset{2K+2}{\sum }}}{b}_p{a}_{{}_{n-p+1}}=0\end{array}$ (67)

where

$\epsilon =\frac{2M}{{\hslash }^2{\alpha }^2}E,d_0=-\frac{2M}{{\hslash }^2{\alpha }^2}\left[C_{-2}+C_{-1}+C_1+C_2+C_3\right]$ (68)

$d_1=\frac{2M}{{\hslash }^2{\alpha }^2}\left[-\frac{2\mathcal{l}\left(\mathcal{l}+1\right){\alpha }^{2}s}{2M}+C_{-1}+3C_1+4C_2+5C_3-{\beta }_1\right]$ (69)

$d_2=\frac{2M}{{\hslash }^2{\alpha }^2}\left[\frac{2\mathcal{l}\left(\mathcal{l}+1\right){\alpha }^{2}s}{2M}-3C_1-6C_2-10C_3-{\beta }_2\right]$ (70)

$\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}{d}_3=\frac{2M}{{\hslash }^2{\alpha }^2}\left(C_1+4C_2+10C_3+{\beta }_3\right),\mathrm{<mtext>\; \hspace{0.17em}\; </mtext>}{d}_4=-\frac{2M}{{\hslash }^2{\alpha }^2}\left(C_2+5C_3+{\beta }_4\right)$ (71)

$d_5=\frac{2M}{{\hslash }^2{\alpha }^2}\left(C_3-{\beta }_5\right);b_j=-\frac{2M}{{\hslash }^2{\alpha }^2}{\beta }_j,j=6,7,\cdots ,2K+2.$ (72)

Here, $d_i$ refers to the coefficient of ${\eta }^i$ in the expression between brackets which intervene in the left-hand side of Equation (64).

It is worth noting that the ${\beta }_j$ quantities that appear in Equations (69)-(72) are defined as follows:

${\beta }_1={\hat{B}}_1;{\beta }_2=-2{\hat{B}}_1+{\hat{B}}_2;{\beta }_j={\hat{B}}_{j-2}-2{\hat{B}}_{j-1}+{\hat{B}}_j;j=3,4,\cdots ,2K;$ (73)

${\beta }_{2K+1}={\hat{B}}_{2K-1}-2{\hat{B}}_{2K};{\beta }_{2K+2}={\hat{B}}_{2K}$ (74)

where the ${\hat{B}}_j$ quantities are calculated from the two following equations :

${\hat{B}}_{2p+1}={\displaystyle \underset{\begin{array}{c}j=p+1\\ j\le K\end{array}}{\overset{2p+1}{\sum }}}{\left(-1\right)}^{j+1}\left(\begin{array}{c}j\\ 2p+1-j\end{array}\right)2^{2j-2p-1}{\tilde{B}}_j;\mathrm{<mtext>\; \hspace{0.17em}\; </mtext>}p=0,\cdots ,K-1;$ (75)

${\hat{B}}_{2p}={\displaystyle \underset{\begin{array}{c}j=p\\ j\le K\end{array}}{\overset{2p}{\sum }}}{\left(-1\right)}^j\left(\begin{array}{c}j\\ 2p-j\end{array}\right)2^{2j-2p}{\tilde{B}}_j;p=1,2,\cdots ,K.$ (76)

Let us mention in passing that the potential (53) has been studied in [18] using variables $\xi$ and $\eta$ given by $\xi =\tanh \left(\tilde{\alpha }r\right)$ and $\eta =\xi -1\in \left[-1,0\right]$.

Setting $n=-1$ in the above recursion relation, we obtain the indicial equation $\left(4{\delta }^2+d_0+\epsilon \right)a_0=0$ which is solved by ${\delta }_1=-\sqrt{-d_0-\epsilon }/2$ and ${\delta }_2=\sqrt{-d_0-\epsilon }/2$. We can therefore conclude that the two solutions of the radial SE obtained as generalized series, one with $\delta ={\delta }_1$ and the other with $\delta ={\delta }_2$, are linearly independent. Clearly, only $\delta >0$ is acceptable for bound states since in this case $\psi \left(r=\infty \right)=\psi \left(\eta =0\right)=0$. Such a solution to the SE contains only the series with $\delta ={\delta }_2$, and in the following will be denoted by

$\psi \left(\eta ,\epsilon \right)={\eta }^{{\delta }_2}{\displaystyle \underset{n=0}{\overset{\infty }{\sum }}}{a}_n{\eta }^n$ (77)

where the dependence on the energy eigenvalue is explicitly marked. For arbitrary $\epsilon$, the wave function $\psi \left(\eta ,\epsilon \right)$ obtained from (77) is not square integrable. If, for a particular value of $\epsilon$, $\psi \left(\eta =0,\epsilon \right)=0$, the wave function is square integrable. In other words, this condition determines the energies of the discrete spectrum. Substituting the calculated bound state energy into the recursion relation (67), the coefficients of the generalized series (77) can be successively determined in order to obtain the wave function as a sum of the series.

We have to emphasize that in practice, the function $\psi \left(\eta ,\epsilon \right)$ has to be approximated by truncating the series in Equation (77) at a suitably high order N, which requires high precision computing since some of the elements of matrices S and P needed to compute the $a_i^{\left[k\right]}$ coefficients (se relations (49) and (50)) are extremely big for high values of i. To deal with this situation, we appeal to a software package for arbitrary precision computation, named MPFUN2015 and developed by David H. Bailey [20]. In our calculations, the precision level is set to 500 digits and $a_0$ equals 10⁻⁹. The number of terms in the series (77) is 602, which means that N = 601. One has to add that the truncated series is a function of ε whose zeros correspond to bound state values of ε. If for two neighboring values of ε the wave function at $\eta =0$ ( $r\to \infty$ ) takes values of different signs, we can deduce that one bound state reduced energy (ε) lies between these two values. The bound state reduced energy in question can be computed numerically by means of the dichotomy method [21] with an arbitrary chosen precision.

Figure 1 shows bound state wave functions as function of r in the case of the so-called Manning-Rosen Potential (MRP) defined by [18] [22] [23] [24] [25]

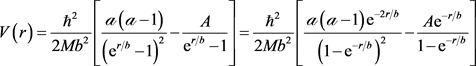(78)

and which is a special case of the potential (53) since this one reduces to MRP by choosing $K=1$, $C_{-2}=a\left(a-1\right){\hslash }^2/\left(8M{b}^2\right)$, $C_{-1}=-\left[a\left(a-1\right)+A\right]{\hslash }^2/\left(4M{b}^2\right)$, $C_1=0$, $C_2=B_1=\left[a\left(a-1\right)+2A\right]{\hslash }^2/\left(8M{b}^2\right)$ and $\alpha =1/\left(2b\right)$.

Figure 2 shows the effective potential $V_{\text{eff}}\left(r\mathrm{,}\mathcal{l}\right)$ given by

$V_{\text{eff}}\left(r\mathrm{,}\mathcal{l}\right)=\frac{\mathcal{l}\left(\mathcal{l}+1\right){\hslash }^2}{2M{r}^2}+V\left(r\right)\mathrm{,}$ (79)

where the dependence on $\mathcal{l}$ is explicitly marked, for the first four values of $\mathcal{l}$ and given values of $a$, b and A.

In our calculations, $\mathcal{l}=1$, the value of $a$ is 0.75, that of 1/b is 0.025, $A=2b$ and the quantum number $n\le 8$. The parameter $b$ has been chosen such that $\tilde{\alpha }=0.0001$, which implies that 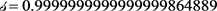and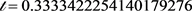. We have seven bound states whose energies, obtained by means of the FM, are: E₂₁ = −0.12054171328 a.u., E₃₁ = −0.04588384531 a.u., E₄₁ = −0.02081525239 a.u., E₅₁ = −0.00981695557 a.u., E₆₁ = −0.00437316621 a.u., E₇₁ = −0.00161118952 a.u. and E₈₁ = −0.00034181936 a.u.

Figure 1. Wave functions as functions of r for 2p-8p states and for $a=0.75$, $1/b=0.025$ and $A=2b$. These functions are normalized such that ${\max }_{r\in \left[\mathrm{0,1000}\right]}\left|{\psi }_{n\mathcal{l}}\left(r\right)\right|=1$. Dashed line: Results obtained by the FM without economization. Solid line: Results of the FM with economization. The asterisk in brackets refers to the fact that the wave function has been obtained after applying the economization procedure to the FM.

Figure 2. The effective potential $V_{\text{eff}}\left(r\right)$ given by Equation (79) for the case $M=m_{\text{e}}$ and parameters $a=0.75$ ; $1/b=0.025$ ; $A=2b$ ; $\mathcal{l}=0,1,2,3$. Atomic units are used, so that $V_{\text{eff}}\left(r\right)$ is expressed in Hartree.

In order to show that our formulas can help to reduce the computation time, we consider the domain $0<r<1000$ and then compute the wave functions at $r_j=0+j{r}_{step}$ for $j=\mathrm{0,1,2,}\cdots \mathrm{,}J$ where the step size $r_{step}=0.001\text{a}.\text{u}.$ and J is the number of the mesh points minus 1. In our case, $J=100,000$, which means that for each bound state, it is necessary to evaluate the sum of the first N + 1 terms of the series intervening in the right-hand side of Equation (77) 100,001 times. Using a (N-k) th-degree economized power series allows to reduce the number of terms in this (N + 1)-term truncated series, which saves us a little time during the computation of the sum. In our calculations, we have chosen $k=200$. We found that the total duration of the whole computation is 9287 seconds (s) when the economization procedure is used to calculate the wave function and 11,540 s in the absence of the economization. The use of the economization procedure thus helps us save 253 s due to the fact that the time spent on computing the $a_i^{\left[k\right]}\left(i=0,1,\cdots ,N-k\right)$ coefficients (see Equations (49) and (50)) is compensated by the gain of time when calculating the (N + 1)-term sum mentioned above.

4. Conclusion

New transformation formulas between finite power series and series of first-kind shifted Chebyshev polynomials are proposed. These formulas have been used to establish formulas that directly turn any Nth-degree truncated power series into an economized one whose degree n is lower than N. We also have shown that the application of these formulas to the Fröbenius and Taylor’s methods for ordinary differential equations can, in some situations, help to reduce the computing time while preserving and even improving the accuracy of the results.

Conflicts of Interest

The authors declare no conflicts of interest regarding the publication of this paper.

References

[1]	López-Bonilla, J., Ramrez-García, E. and Sasa-Caraveo, C. (2010) Power Expansion in Terms of Shifted Chebyshev-Lanczos Polynomials. Revista Notas de Matemtica, 6, 18-22.
[2]	Lanczos, C. (1956) Applied Analysis. Prentice-Hall, Inc., Englewood Cliffs.
[3]	Kreyszig, G.E. (2011) Advanced Engineering Mathematics. 10th Edition, John Wiley & Sons Ltd., Amsterdam.
[4]	Greenberg, M.D. (1998) Advanced Engineering Mathematics. 2th Edition, Simon & Schuster Asia Pte, Ltd., Singapore.
[5]	Bekir, E. (2019) Efficient Chebyshev Economization for Elementary Functions. Communications Faculty of Sciences University of Ankara Series A2-A3 Physical Sciences and Engineering, 61, 33-56. http://communications.science.ankara.edu.tr/index.php?series=A2-A3
[6]	Hamming, R.W. (1973) Numerical Methods for Scientists and Engineers. 2nd Edition, Dover Publications, Inc., Mineola.
[7]	Fletcher, C.A.J. (1984) Computational Galerkin Methods. 1st Edition, Springer-Verlag, New York. https://doi.org/10.1007/978-3-642-85949-6
[8]	Gil, A., Segura, J. and Temme, N.M. (2007) Numerical methods for Special Functions. First Edition, Society for Industrial and Applied Mathematics, Philadelphia. https://doi.org/10.1137/1.9780898717822
[9]	Cody, W.J. (1970) A Survey of Practical Rational and Polynomial approximation of Functions. SIAM Review, 12, 400-423. https://www.jstor.org/stable/2028556 https://doi.org/10.1137/1012082
[10]	Mason, J.C. and Handscomb, D.C. (2002) Chebyshev Polynomials. First Edition, Chapman and Hall/CRC, New York. https://doi.org/10.1201/9781420036114
[11]	Spanier, J. and Oldham, K.B. (1987) An Atlas of Functions. Hemisphere Publication Corporation/Springer-Verlag, New York.
[12]	Press, W.H., Teukolsky, S.A., Vetterling, T.T. and Flanney, B.P. (2007) Numerical Recipes. Third Edition: The Art of Scientific Computing. Cambridge University Press, New York.
[13]	Unruh, P.F. (1968) Chebyshev Aproximations. Masters Report. Kansas State University, Manhattan. https://ia800706.us.archive.org/25/items/chebyshevapproxi00unru/chebyshevapproxi00unru.pdf
[14]	Burden, R.L. and Faires, J.D. (2010) Numerical Analysis. 9th Edition, Brooks/Code, Cengage Learning, Boston. https://fac.ksu.edu.sa/sites/default/files/numerical_analysis_9th.pdf
[15]	Imad Omar Faris, K. (2013) Error Analysis and Stability of Numerical Schemes for Initial Value Problems “IVP’s”. Master’s Thesis, Faculty of Graduate Studies, ANn-Majah Natinal University, Nablus. https://repository.najah.edu/handle/20.500.11888/8543
[16]	Nyengeri, H., Manariyo, B., Nizigiyimana, R. and Mugisha, S. (2020) Application of the Economization of Power Series to Solving The Schrödinger Equation for the Gaussian Potential via the Asymptotic Iteration Method. Open Access Library Journal, 7, e6505. https://dx.doi.org/10.4236/oalib.1106505
[17]	Ake, B. and Germund, D. (2008) Numerical Methods in Scientific Computing. Vol. 2, Society for Industrial and Applied Mathematics, Philadelphia.
[18]	Nyengeri, H., Nizigiyimana, R., Ndenzako, E., Bigirimana, F., Niyonkuru, D. and Girukwishaka, A. (2018) Application of the Fröbenius Method to the Schrödinger Equation for a Spherically Symmetric Hyperbolic Potential. Open Access Library Journal, 5, e4950. https://doi.org/10.4236/oalib.1104950
[19]	Chen, C.Y., Lu, F.L. and You, Y. (2012) Scattering States of Modified Pöschl-Teller Potential in D-Dimension. Chinese Physics B, 21, Article ID: 030302. https://doi.org/10.1088/1674-1056/21/3/030302
[20]	Baily, D.H. (2015) A Thread-Safe Arbitrary Precision Computation Package. http://www.davidhbailey.com/dhbpapers/mpfun2015.pdf
[21]	Kincaid, D. and Chemey, W. (2002) Numerical Analysis: The Mathematics of Scientific Computing. 3rd Edition, American Mathematical Society, Pacific Groove.
[22]	Dong, S.H. and Garcia-Ravalo, J. (2007) Exact Solutions of the s-Wave Schrödinger Equation with Manning-Rosen Potantial. Physica Scripta, 75, 307-309. https://doi.org/10.1088/0031-8949/75/3/013
[23]	Qiang, W.C. and Dong, S.H. (2009) The Manning-Rosen Potential Studied by a New Approximation Scheme to the Centrifugal Term. Physica Scripta, 79, Article ID: 045004. https://doi.org/10.1088/0031-8949/79/04/045004
[24]	Roy, A.K. (2014) Studies of Bound States Spectra of Manning-Rosen Potential. Modern Physics Letters A, 29, Article ID: 1450042. https://doi.org/10.1142/S0217732314500424
[25]	Ikhdair, S.M. (2011) On the Bound-State Solutions of the Manning-Rosen Potential Including Improved Approximation to the Orbital Centrifugal Term. Physica Scripta, 83, Article ID: 015010. https://doi.org/10.1088/0031-8949/83/01/015010