In this article, we start by a review of the circle group
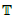
[1] and its topology induced [1] by the quotient metric, which we later use to define a topological structure on the unit circle
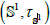
. Using points on

under the complex exponential map, we can construct orthogonal projection operators. We will show that under this construction, we arrive at a topological group, denoted

of projection matrices. Together with the induced topology, it will be demonstrated that

is Hausdorff and Second Countable forming a topological manifold. Moreover, I will use an example of a group action on
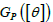
to generate subgroups of
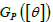
.