Let
D be a digraph. A subset
S of
V (D) is a
stable set if every pair of vertices in
S is non-adjacent in
D. A collection of disjoint paths
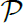
is a
path partition of
D, if every vertex in
V (D) is in exactly one path of
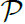
. We say that a stable set
S and a path partition

are
orthogonal if each path of
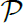
contains exactly one vertex of
S. A digraph
D satisfies the
α-property if for every maximum stable set
S of
D, there exists a path partition
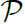
such that
S and

are orthogonal. A digraph
D is
α-diperfect if every induced subdigraph of
D satisfies the
α-property. In 1982, Berge proposed a characterization for
α-diperfect digraphs in terms of forbidden
anti-directed odd cycles. In 2018, Sambinelli, Silva and Lee proposed a similar conjecture. A digraph
D satisfies the
Begin-End-property or
BE-property if for every maximum stable set
S of
D, there exists a path partition
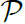
such that 1)
S and
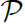
are orthogonal and 2) for each path
P ∈ 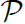
, either the start or the end of
P belongs to
S. A digraph
D is
BE-diperfect if every induced subdigraph of
D satisfies the BE-property. Sambinelli, Silva and Lee proposed a characterization for BE-diperfect digraphs in terms of forbidden
blocking odd cycles. In this paper, we verified both conjectures for 3-anti-circulant digraphs. We also present some structural results for
α-diperfect and BE-diperfect digraphs.