A Comparison of the Estimators of the Scale Parameter of the Errors Distribution in the L1 Regression ()
ABSTRACT
The L1 regression is a robust alternative to
the least squares regression whenever there are outliers in the values of the response
variable, or the errors follow a long-tailed distribution. To
calculate the standard errors of the L1 estimators, construct confidence
intervals and test hypotheses about the parameters of the model, or to calculate
a robust coefficient of determination, it is necessary to have an estimate of a
scale parameterτ. This parameter is such
that τ2/n is
the variance of the median of a sample of size n from the errors
distribution. [1] proposed
the use of , a consistent, and so, an asymptotically unbiased estimator of τ. However, this estimator is not stable in small samples, in the sense that it can
increase with the introduction of new independent variables in the model. When
the errors follow the Laplace distribution, the maximum likelihood estimator of τ, say 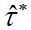 , is the mean absolute error, that is, the mean of the absolute residuals.
This estimator always decreases when new independent variables are added to the
model. Our
objective is to develop asymptotic properties of
, is the mean absolute error, that is, the mean of the absolute residuals.
This estimator always decreases when new independent variables are added to the
model. Our
objective is to develop asymptotic properties of 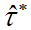 under several errors distributions analytically.
We also performed a simulation study to compare the distributions of both estimators
in small samples with the objective to establish conditions in which
under several errors distributions analytically.
We also performed a simulation study to compare the distributions of both estimators
in small samples with the objective to establish conditions in which 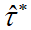 is a good
alternative to
is a good
alternative to 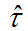 for such situations.
for such situations.
Share and Cite:
de André, C. and Elian, S. (2022) A Comparison of the Estimators of the Scale Parameter of the Errors Distribution in the L
1 Regression.
Open Journal of Statistics,
12, 261-276. doi:
10.4236/ojs.2022.122018.
Cited by
No relevant information.