Author(s)

Ruixian Fang, Dan Gabriel Cacuci^*

Center for Nuclear Science and Energy, Department of Mechanical Engineering, University of South Carolina, Columbia, SC, USA.

This work presents the results of the exact computation of (180)³ = 5,832,000 third-order mixed sensitivities of the leakage response of a polyethylene-reflected plutonium (PERP) experimental benchmark with respect to the benchmark’s 180 microscopic total cross sections. This computation was made possible by applying the Third-Order Adjoint Sensitivity Analysis Methodology developed by Cacuci. The numerical results obtained in this work revealed that many of the 3^rd-order sensitivities are significantly larger than their corresponding 1^st- and 2^nd-order ones, which is contrary to the widely held belief that higher-order sensitivities are all much smaller and hence less important than the first-order ones, for reactor physics systems. In particular, the largest 3^rd-order relative sensitivity is the mixed sensitivity of the PERP leakage response with respect to the lowest energy-group (30) total cross sections of ¹H (“isotope 6”) and ²³⁹Pu (“isotope 1”). These two isotopes are shown in this work to be the two most important parameters affecting the PERP benchmark’s leakage response. 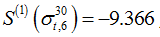By comparison, the largest 1^st-order sensitivity is that of the PERP leakage response with respect to the lowest energy-group total cross section of isotope ¹H, having the value , while the largest 2^nd-order sensitivity is . The 3^rd-order sensitivity analysis presented in this work is the first ever such analysis in the field of reactor physics. The consequences of the results presented in this work on the uncertainty analysis of the PERP benchmark’s leakage response will be presented in a subsequent work.

Polyethylene-Reflected Plutonium Sphere, 1^st-Order Sensitivities, 2^nd-Order Sensitivities, 3^rd-Order Sensitivities, Third Order Adjoint Sensitivity Analysis, Microscopic Total Cross Sections

Fang, R.X. and Cacuci, D.G. (2020) Third Order Adjoint Sensitivity and Uncertainty Analysis of an OECD/NEA Reactor Physics Benchmark: II. Computed Sensitivities. American Journal of Computational Mathematics, 10, 529-558. doi: 10.4236/ajcm.2020.104030.