Grandi’s paradox, which was posed for a real function of the form
1/(1+ x), has been resolved and extended to complex valued functions. Resolution of this approximately three-hundred-year-old paradox is accomplished by the use of a consistent truncation approach that can be applied to all the series expansions of Grandi-type functions. Furthermore, a new technique for improving the convergence characteristics of power series with alternating signs is introduced. The technique works by successively averaging a series at different orders of truncation. A sound theoretical justification of the successive averaging method is demonstrated by two different series expansions of the function
1/(1+ ex ) . Grandi-type complex valued functions such as
1/(i + x) are expressed as consistently-truncated and convergence-improved forms and Fagnano’s formula is established from the series expansions of these functions. A Grandi-type general complex valued function
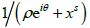
is introduced and expanded to a consistently truncated and successively averaged series. Finally, an unorthodox application of the successive averaging method to polynomials is presented.