Author(s)

Antony J. Bourdillon

UHRL, San Jose, USA.

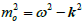
From a combination of Maxwell’s electromagnetism with Planck’s law and the de Broglie hypothesis, we arrive at quantized photonic wave groups whose constant phase velocity is equal to the speed of light c = ω/k and to their group velocity dω/dk. When we include special relativity expressed in simplest units, we find that, for particulate matter, the square of rest mass , i.e., angular frequency squared minus wave vector squared. This equation separates into a conservative part and a uniform responsive part. A wave function is derived in manifold rank 4, and from it are derived uncertainties and internal motion. The function solves four anomalies in quantum physics: the point particle with prescribed uncertainties; spooky action at a distance; time dependence that is consistent with the uncertainties; and resonant reduction of the wave packet by localization during measurement. A comparison between contradictory mathematical and physical theories leads to similar empirical conclusions because probability amplitudes express hidden variables. The comparison supplies orthodox postulates that are compared to physical principles that formalize the difference. The method is verified by dual harmonics found in quantized quasi-Bloch waves, where the quantum is physical; not axiomatic.

Wave Packet, Reduction, Phase Velocity, Hidden Variables, Young’s Slits, Resonant Response, Dispersion Dynamics, Quantum Physics

Bourdillon, A. (2023) Quantum Mechanics: Harmonic Wave-Packets, Localized by Resonant Response in Dispersion Dynamics. Journal of Modern Physics, 14, 171-182. doi: 10.4236/jmp.2023.142012.