Random Crank-Nicolson Scheme for Random Heat Equation in Mean Square Sense

M. T. Yassen, M. A. Sohaly, Islam Elbaz

Department of Mathematics, Faculty of Science, Mansoura University, Mansoura, Egypt.

DOI: 10.4236/ajcm.2016.62008                

Abstract

The goal of computational science is to develop models that predict phenomena observed in nature. However, these models are often based on parameters that are uncertain. In recent decades, main numerical methods for solving SPDEs have been used such as, finite difference and finite element schemes [1]-[5]. Also, some practical techniques like the method of lines for boundary value problems have been applied to the linear stochastic partial differential equations, and the outcomes of these approaches have been experimented numerically [7]. In [8]-[10], the author discussed mean square convergent finite difference method for solving some random partial differential equations. Random numerical techniques for both ordinary and partial random differential equations are treated in [4] [10]. As regards applications using explicit analytic solutions or numerical methods, a few results may be found in [5] [6] [11]. This article focuses on solving random heat equation by using Crank-Nicol- son technique under mean square sense and it is organized as follows. In Section 2, the mean square calculus preliminaries that will be required throughout the paper are presented. In Section 3, the Crank-Nicolson scheme for solving the random heat equation is presented. In Section 4, some case studies are showed. Short conclusions are cleared in the end section.

Keywords

Random Partial Differential Equations (RPDEs), Mean Square Sense (m.s), Second Order Random Variable (2r.v.'s), Random Crank-Nicolson Scheme, Convergence, Consistency, Stability

Received 2 February 2016; accepted 5 February 2016; published 3 June 2016

1. Introduction

The goal of computational science is to develop models that predict phenomena observed in nature. However, these models are often based on parameters that are uncertain. In recent decades, main numerical methods for solving SPDEs have been used such as, finite difference and finite element schemes [1] - [5] . Also, some practical techniques like the method of lines for boundary value problems have been applied to the linear stochastic partial differential equations, and the outcomes of these approaches have been experimented numerically [7] . In [8] - [10] , the author discussed mean square convergent finite difference method for solving some random partial differential equations. Random numerical techniques for both ordinary and partial random differential equations are treated in [4] [10] . As regards applications using explicit analytic solutions or numerical methods, a few results may be found in [5] [6] [11] . This article focuses on solving random heat equation by using Crank-Nicol- son technique under mean square sense and it is organized as follows. In Section 2, the mean square calculus preliminaries that will be required throughout the paper are presented. In Section 3, the Crank-Nicolson scheme for solving the random heat equation is presented. In Section 4, some case studies are showed. Short conclusions are cleared in the end section.

2. Preliminaries

Definition 2.1. Let us take in to consideration that, the properties of a class of real random variables

whose second moments, 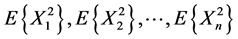are finite. In this case they are

called second order random variables.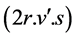

Definition 2.2. A sequence of 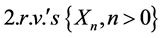is mean square convergent to a random variable X if: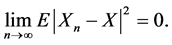

3. Random Crank-Nicolson Scheme (RCNS)

If we have the linear random heat problem of the form:

(1)

Where is a second order random variable.

(2)

(3)

Then, we can find the random Crank-Nicolson scheme for this problem as follows:

Take a uniform mesh with step size 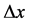and on x-axis and t-axis respectively. Additionally, Let 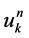approximates u(x, t) at point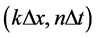. Hence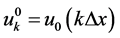. On this mesh we have:

Then,

Similarly,

Then,

Hence for (1):

Put

Hence, the RCNS for our problem is:

(4)

(5)

(6)

3.1. Consistency of RCNS

We can rewrite the above scheme as:

The above scheme is a random Crank-Nicolson version of (1 - 3). For a RPDE, say Lv = G where L is a differentiable operator and. On the other hand, we represent finite difference scheme at the point by.

Definition 3.1.1. A random difference scheme that approximating RPDE Lv = G is consistent in mean square sense at time, if for any continuously differentiable function, we have in mean square:

As and

Theorem 3.1.1. The random Crank-Nicolson difference scheme (4)-(6) with second order random variable is to be consistent in mean square sense as: and.

Proof. Assume that is a deterministic smooth function then:

Then,

As:, and at time, Then we have

Hence, the random Crank-Nicolson scheme (4)-(6) is consistent in mean square sense.∎

3.2. Exponential Stability Analysis of RCNS

Definition 3.2.1. A random Crank-Nicolson difference scheme is exponential stable in mean square if there exist some positive constants a, c and constants k, b. Such that:

For: and

Theorem 3.2.1. The random Crank-Nicolson scheme (4)-(6) with second order random variable is unconditionally stable in mean square sense as with k = 1 and b = 0.

Proof: Since,

Then,

Finally, we have:

At: then, we have:

Hence, the random Crank-Nicolson difference scheme with second order random variable is unconditionally stable with and. ∎

3.3. Convergence of RCNS

Definition 3.3.1. A random difference scheme that approximating RPDE Lv = G is convergent in mean square sense at time, if:

, as and

Theorem 3.3.1. The random Crank-Nicolson difference scheme (4)-(6) with second order random variables is convergent in mean square sense.

Proof.

Since, the RCNS is consistent and unconditionally exponential stable, thus, the scheme (4)-(6) is convergent in mean square sense.∎

4. Case Studies

Consider the linear random parabolic partial differential equation:

With initial condition

(7)

and the boundary conditions

And is a second order random variable.

4.1. The Exact Relation

(8)

4.2. The Numerical Solution

The Random Crank-Nicolson Difference Scheme for this problem is

(9)

where, and

Substituting by in (9) we have:

Putting n = 0 in the above system then we have:

Then, we have the system:

From this system we have:

Verification for the Convergence of Mean

(1) Changing step size

・ Choosing:

・ Choosing:

(2) Changing step size

・ Choosing:

・ Choosing:

(3) Changing the expectations

・ Choosing:

・ Choosing:

From these tables we note that the error is acceptable if:

1) The changing happens in when are constant values.

2) The changing happens in when are constant values.

3) The changing happens in when are constant values.

5. Conclusion

The random heat equation can be solved numerically by using mean square convergent Crank-Nicolson scheme. The random variable in the Crank-Nicolson scheme is must second order random variable and the random Crank-Nicolson scheme is unconditionally stable in the area of mean square sense. Many complicated equations in linear and nonlinear parabolic partial differential problems can be discussed using finite difference schemes in mean square sense.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Soong, T.T. (1973) Random Differential Equations in Science and Engineering. Academic Press, New York.
[2]	Thomas, J. (1998) Numerical Partial Differential Equations: Finite Difference Methods, Texts in Applied Mathematics. Springer.
[3]	Allen, E.J., Novosel, S.J. and Zhang, Z.C. (1998) Finite Element and Difference Approximation of Some Linear Stochastic Partial Differential Equations. Stochastics and Stochastic Reports, 64, 117-142. http://dx.doi.org/10.1080/17442509808834159
[4]	Davie, A.J. and Gaines, J.G. (2001) Convergence of Numerical Schemes for the Solution of Parabolic Stochastic Partial Differential Equations. Mathematics of Computations, 70, 121-134. http://dx.doi.org/10.1090/S0025-5718-00-01224-2
[5]	McDonald, S. (2006) Finite Difference Approximation for Linear Stochastic Partial Differential Equation with Method of Lines. MPRA Paper, 3983.
[6]	Cortes, J.C., Lucas Jódar, L. and Villafuerte, R.J. (2007) Villanueva: Computing Mean Square Approximations of Random Diffusion Models with Source Term. Mathematics and Computers in Simulation, 76, 44-48. http://dx.doi.org/10.1016/j.matcom.2007.01.020
[7]	El-Tawil, M.A. and Sohaly, M.A. (2009) Mean Square Numerical Methods for Initial Value Random Differential Equations. Open Journal of Discrete Mathematics (OJDM), 1, 66-84,
[8]	El-Tawil, M.A. and Sohaly, M.A. (2012) Mean Square Convergent Three Points Finite Difference Scheme for Random Partial Differential Equations. Journal of the Egyptian Mathematical Society, 20, 188-204. http://dx.doi.org/10.1016/j.joems.2012.08.017
[9]	Sohaly, M.A. (2014) Mean Square Heun’s Method Convergent for Solving Random Differential Initial Value Problems of First Order. American Journal of Computational Mathematics, 4, 280-288.
[10]	Mohammed, A.S. (2014) Mean Square Convergent Three and Five Points Finite Difference Scheme for Stochastic Parabolic Partial Differential Equations. Electronic Journal of Mathematical Analysis and Applications, 2, 164-171.
[11]	Mohammed, W., Sohaly, M.A., El-Bassiouny, A. and Elnagar, K. (2014) Mean Square Convergent Finite Difference Scheme for Stochastic Parabolic PDEs. American Journal of Computational Mathematics, 4, 280-288. http://dx.doi.org/10.4236/ajcm.2014.44024