Topological Properties of the Catastrophe Map of a General Equilibrium Production Model with Uncertain States of Nature ()
1. Introduction
This paper considers the Arrow-Debreu model with a complete set of contingent claims [1] and production. Existence and efficiency of equilibria of this model are shown by [2] in a seminal paper. This paper, however, derives global topological properties of the set of equilibria. The structure of this set has been studied before by Balasko [3] in the context of deterministic pure exchange economics. Such models lack a time structure, and as a consequence do not incorporate uncertainty [3] - [5] (Balasko (Preprint 2011) for example).1
The aim of this paper is to consider a reformulation of the Arrow-Debreu model in terms of an exchange model with production in the utility function. Preliminary results are found in [6] . A version of the decentralized production model is found in [7] . The formulation of the production model considered in this paper allows extending some of the known results about deterministic economies to production economies with uncertainty and production of adjusted demand functions. It is shown that the set of equilibria is a smooth manifold. Its dimension depends on the number of goods available for consumption, the number of uncertain states of nature and the number of consumers. This manifold is also shown to be diffeomorphic to a sphere. This result has deep economic implication. It implies that geodesics can be defined on it. This property is particularly useful when designing economic policies.
The paper is organized in three sections. Section 2 introduces the model. Section 3 establishes the results, and Section 4 is a conclusion.
2. The Long Run Private Ownership Production Model with Uncertain States of Nature
We describe the two period private ownership production model 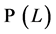 introduced in [1] , chapter 7. Uncertainty is defined by a finite set of mutually exclusive and exhaustive states of nature denoted by
introduced in [1] , chapter 7. Uncertainty is defined by a finite set of mutually exclusive and exhaustive states of nature denoted by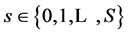 , where s = 0 is the certain event in time period one. In total there are S + 1 states of nature. There are
, where s = 0 is the certain event in time period one. In total there are S + 1 states of nature. There are 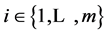 consumers,
consumers,  producers, and
producers, and 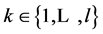 physical goods. For all consumers
physical goods. For all consumers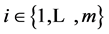 , a consumption bundle is a collection of vectors
, a consumption bundle is a collection of vectors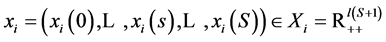 , where consump-
, where consump-
tion in a particular state 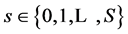 is a vector
is a vector . Associated with physical
. Associated with physical
commodities is a set of normalized prices, denoted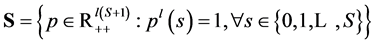 . Consumers
. Consumers
are further endowed with a fraction 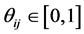 of the profits of each firm.
of the profits of each firm. 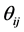 represents the exogenously determined ownership structure of the private ownership production economy. It satisfies for each
represents the exogenously determined ownership structure of the private ownership production economy. It satisfies for each  and
and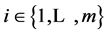 ,
,  , and
, and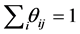 . Denote the set of ownership structures
. Denote the set of ownership structures
![]() .
.
Consumers are endowed with a collection of vectors of initial resources
![]() ,
,
where initial endowments in a particular state ![]() is a vector
is a vector![]() . Consumer
. Consumer ![]() is further characterized by a smooth Marschallian demand function
is further characterized by a smooth Marschallian demand function
![]() ,
,
where ![]() is defined for price vector
is defined for price vector ![]() and wealth level
and wealth level ![]() [8] , where
[8] , where![]() .2
.2
Producers are characterized by production sets and their smooth supply functions. The main property of the long run production model is that all activities of the firm are variable. An activity ![]() is a collection of vectors
is a collection of vectors![]() , where an activity in state
, where an activity in state ![]() is a vector of inputs
is a vector of inputs
![]() , and
, and ![]() is the associated vector of outputs in
is the associated vector of outputs in
state![]() . Let
. Let ![]() denote the smooth supply function of firm
denote the smooth supply function of firm![]() , where
, where ![]() is defined on the set of normalized prices. Standard assumptions of smooth production economies introduced in [1] hold for each production set
is defined on the set of normalized prices. Standard assumptions of smooth production economies introduced in [1] hold for each production set![]() . In particular
. In particular ![]() is convex,
is convex, ![]() , and
, and ![]() has a strictly positive Gaussian curvature for every
has a strictly positive Gaussian curvature for every![]() .
.
2.1. Equilibrium ![]()
Each consumer ![]() chooses a utility maximizing consumption bundle
chooses a utility maximizing consumption bundle ![]() at fixed
at fixed ![]() and
and ![]() satisfying his budget constraints. Each producer
satisfying his budget constraints. Each producer ![]() chooses profit maximizing net activities
chooses profit maximizing net activities ![]() at competitive prices
at competitive prices![]() . Let
. Let
![]() (1)
(1)
be the market excess demand function in state![]() . Then, market clearance requires demand to equal supply in each market and uncertain state of the world. Hence
. Then, market clearance requires demand to equal supply in each market and uncertain state of the world. Hence
![]()
An equilibrium is a price vector ![]() which satisfies this equation for a fixed distribution of initial resources and exogenously given ownership structure. An equilibrium pair is an equilibrium price vector
which satisfies this equation for a fixed distribution of initial resources and exogenously given ownership structure. An equilibrium pair is an equilibrium price vector ![]() with associated
with associated![]() . An equilibrium allocation is an allocation
. An equilibrium allocation is an allocation ![]() associated with an equilibrium price
associated with an equilibrium price![]() . The model of the consumer is to solve a constraint optimization problem. This requires a consumer to maximize utility subject to a sequence of
. The model of the consumer is to solve a constraint optimization problem. This requires a consumer to maximize utility subject to a sequence of ![]() budget constraints. Hence, each consumer
budget constraints. Hence, each consumer ![]()
![]()
where ![]() is the consumer’s smooth3 utility function. The new production adjusted budget set is now defined by
is the consumer’s smooth3 utility function. The new production adjusted budget set is now defined by
![]()
The model of the producer is to maximize profits. Each producer solves a constraint optimization profit maximization problem. Hence, each ![]()
![]()
where the state dependent production set ![]() for all
for all ![]() satisfies the assumptions of Debreu [1] also stated in the pervious section for the deterministic case.
satisfies the assumptions of Debreu [1] also stated in the pervious section for the deterministic case.
Definition 1. An equilibrium of the two period private ownership production model with uncertainty ![]() is a price vector
is a price vector ![]() at fixed pair
at fixed pair ![]() if for utility maximizing consumers
if for utility maximizing consumers ![]() and profit maximizing producers
and profit maximizing producers ![]()
![]() (2)
(2)
An equilibrium allocation is a pair ![]() associated with an equilibrium price vector
associated with an equilibrium price vector ![]() for fixed parameters
for fixed parameters![]() . Let , denote the mathematical operation defined by a state by state inner product. There are
. Let , denote the mathematical operation defined by a state by state inner product. There are ![]() equilibrium equations less
equilibrium equations less ![]() equations satisfying Walras’ law
equations satisfying Walras’ law![]() , hence we have a system of
, hence we have a system of ![]() linearly independent equations. This amounts to the number of unknowns, given the number of normalized prices of
linearly independent equations. This amounts to the number of unknowns, given the number of normalized prices of![]() .
.
A study of the qualitative equilibrium structure of the two period private ownership production model with uncertainty amounts to a study of the structure of the solution set of the equilibrium equation![]() . The first result is an equivalence relation between the two period exchange model with uncertainty and the two period production model with uncertainty. The relation between these models follows from the definition of a two period exchange model with production adjusted Marshallian demand functions.
. The first result is an equivalence relation between the two period exchange model with uncertainty and the two period production model with uncertainty. The relation between these models follows from the definition of a two period exchange model with production adjusted Marshallian demand functions.
Let ![]() for any price system
for any price system ![]() and uncertain state of the world
and uncertain state of the world
![]() . Let
. Let ![]() defined by
defined by![]() , where hi(s) is given by
, where hi(s) is given by
![]() (3)
(3)
denote the individual demand function of the two period “production adjusted” exchange model![]() , where for every
, where for every ![]() ownership structure
ownership structure ![]() is fixed, and total wealth defined by
is fixed, and total wealth defined by
![]()
in every![]() . Now, let the equilibrium equation of the production model
. Now, let the equilibrium equation of the production model ![]() be given by
be given by
![]()
where
![]() (4)
(4)
denotes the individual demand function. This follows immediately from rewriting the excess demand equation in terms of demand equal to supply. Rewriting ![]() in terms of ownership
in terms of ownership![]() , summing over
, summing over![]() , and using
, and using ![]() yields
yields
![]()
Hence, the equilibrium equation of the production model ![]() writes
writes
![]()
since![]() . This can be rewritten as
. This can be rewritten as
![]()
This is the equilibrium equation of the exchange model with production adjusted demand functions![]() . Hence, by definition of the production adjusted demand function
. Hence, by definition of the production adjusted demand function ![]() obtain
obtain
![]() (5)
(5)
since ![]() for all
for all![]() . This is the equilibrium equation of the production adjusted exchange model
. This is the equilibrium equation of the production adjusted exchange model ![]() in terms of
in terms of![]() . This concludes the proof of theorem (1).
. This concludes the proof of theorem (1).
Theorem 1. For fixed![]() ,
, ![]() is an equilibrium of the long run production model with uncertainty
is an equilibrium of the long run production model with uncertainty ![]() if and only if
if and only if ![]() is an equilibrium of the two period exchange model with uncertainty and production adjusted demand functions
is an equilibrium of the two period exchange model with uncertainty and production adjusted demand functions![]() .
.
We have established a relationship between the production model with a long term time structure and uncertainty![]() , and a pure exchange model with a long term time structure and uncertainty with production adjusted demand functions
, and a pure exchange model with a long term time structure and uncertainty with production adjusted demand functions![]() .
.
The result suggests that the decentralized production model can be reformulated as a centralized model. It is efficiently applied in establishing many properties about production economies in the next section.
2.2. Equilibrium Structure ![]() of
of ![]()
Let ![]() denote the set of equilibrium solutions of the production adjusted exchange model
denote the set of equilibrium solutions of the production adjusted exchange model ![]() or the set of solutions of the long run production model
or the set of solutions of the long run production model![]() .4 This set consists of pairs
.4 This set consists of pairs ![]() satisfying the equilibrium equations
satisfying the equilibrium equations![]() . Formally, for the case of the production model
. Formally, for the case of the production model ![]() we have
we have
![]()
and in the case of the production adjusted exchange model![]() , we have
, we have
![]()
Theorem 2. The set ![]() of model
of model ![]() is a closed subset of the Euclidean space defined by
is a closed subset of the Euclidean space defined by![]() .
.
Proof. ![]() is defined by pairs
is defined by pairs ![]() satisfying the equilibrium Equation (5).
satisfying the equilibrium Equation (5). ![]() is the preimage of the vector
is the preimage of the vector ![]() by the smooth mapping
by the smooth mapping ![]() for all
for all![]() , and closed by the closed map lemma closed ([9] , p. 553). The closed map lemma requires the excess demand mapping to be continuous and the domain to be a compact set and the range a Hausdorff space. Recall that the excess demand mapping is differentiable at any order required. This is a consequence of subtracting differentiable aggregate supply mappings from differentiable aggregate demand mappings. Differentiability of demand and supply mappings is in turn a consequence of the assumptions of the model discussed earlier ([1] [8] ).
, and closed by the closed map lemma closed ([9] , p. 553). The closed map lemma requires the excess demand mapping to be continuous and the domain to be a compact set and the range a Hausdorff space. Recall that the excess demand mapping is differentiable at any order required. This is a consequence of subtracting differentiable aggregate supply mappings from differentiable aggregate demand mappings. Differentiability of demand and supply mappings is in turn a consequence of the assumptions of the model discussed earlier ([1] [8] ). ![]()
Theorem 3. The set ![]() of model
of model ![]() is a smooth manifold of dimension
is a smooth manifold of dimension![]() .
.
Proof. Consider the mapping ![]() into
into ![]() defined by the smooth mapping
defined by the smooth mapping
![]() .
.
By theorem the regular value theorem ![]() is the preimage of
is the preimage of![]() . We need to prove that this mapping does not contain critical points. This follows by showing that the linear tangent map
. We need to prove that this mapping does not contain critical points. This follows by showing that the linear tangent map ![]() is onto. The onto property follows directly from the rank property of the Jacobian matrix chosen for any arbitrary individual
is onto. The onto property follows directly from the rank property of the Jacobian matrix chosen for any arbitrary individual ![]() and state of nature
and state of nature![]() . By the chain rule, we obtain
. By the chain rule, we obtain
![]()
By simple algebraic manipulations we obtain the new matrices
![]()
![]()
Finally, we obtain
![]()
from which we extract the information required. Rank ![]() is equal to
is equal to ![]() in every state
in every state![]() . By the regular value theorem
. By the regular value theorem ![]() is a smooth manifold. This manifold is parameterized by smooth coordinate functions
is a smooth manifold. This manifold is parameterized by smooth coordinate functions![]() . From the regular value theorem it also follows that its dimension is equal to the dimension of
. From the regular value theorem it also follows that its dimension is equal to the dimension of ![]() minus
minus![]() , hence
, hence
![]() .
.
The following theorem illustrates other economically interesting global properties of the equilibrium manifold. It says that by construction of a diffeomorphism ![]() restricted to the equilibrium manifold
restricted to the equilibrium manifold ![]() into
into
![]() that
that ![]() is diffeomorphic to the sphere in
is diffeomorphic to the sphere in ![]() implying that the equilibrium manifold is arc-connected, simply connected, and contractible. These properties are particularly useful in applied work such as economic policy equilibrium analysis.5 For example, economic policy is often concerned with finding a path between a current point on
implying that the equilibrium manifold is arc-connected, simply connected, and contractible. These properties are particularly useful in applied work such as economic policy equilibrium analysis.5 For example, economic policy is often concerned with finding a path between a current point on ![]() and a desired point on
and a desired point on![]() .
.
Theorem 4. The smooth equilibrium manifold ![]() of model
of model ![]() is diffeomorphic to the sphere of dimension
is diffeomorphic to the sphere of dimension![]() .
.
Proof. The aim of the proof is to define two smooth mappings between smooth manifolds such that we can apply the theorem (Hirsch [10] , pp. 15-16). Hence, let
![]()
be smooth mappings defined by
![]()
Then, let
![]()
denote smooth mappings defined by
![]()
Observe that the coordinates for the ![]() good of the m − 1 consumers in
good of the m − 1 consumers in![]() ,
, ![]() are defined
are defined
![]() (6)
(6)
Also observe that the coordinates for the ![]() consumer of the
consumer of the ![]() goods in
goods in![]() ,
, ![]() are defined by
are defined by
![]() (7)
(7)
The application of theorem ([10] ) requires to show that ![]() and that
and that![]() . The first part of the proof requires to calculate two inclusions, (i)
. The first part of the proof requires to calculate two inclusions, (i) ![]() and (ii)
and (ii)![]() . We start by showing the se- cond part first. Now, to show that (i)
. We start by showing the se- cond part first. Now, to show that (i)![]() , take any consumption bundle
, take any consumption bundle
![]() ,
,
and compute the inner product of (7) with ![]()
![]() , and apply Walras’ law to obtain
, and apply Walras’ law to obtain
![]()
From that a reformulation of (7) readily follows in terms of the equilibrium equation
![]()
This is the equilibrium Equation (5), hence![]() . Next, need to show that (ii)
. Next, need to show that (ii)![]() . Take
. Take![]() . It is then trivial to do the computations proving following equality
. It is then trivial to do the computations proving following equality
![]()
from which it readily follows that![]() . Clearly we have constructed the two smooth relations such that
. Clearly we have constructed the two smooth relations such that
![]()
where ![]() is the identity map defined on
is the identity map defined on![]() . We have shown that the smooth mapping
. We have shown that the smooth mapping ![]() restricted to the equilibrium manifold
restricted to the equilibrium manifold ![]() defines a diffeomorphism between
defines a diffeomorphism between ![]() and the sphere of dimension
and the sphere of dimension![]() .
. ![]()
It remains to be shown that equilibria in the long run production model with uncertainty always exist. The strategy of the proof is to show that the natural projection mapping ![]() is smooth and proper. Existence of long run equilibria of the production model with uncertainty follows immediately from the smoothness lemma (1) and the properness lemma (2) below.
is smooth and proper. Existence of long run equilibria of the production model with uncertainty follows immediately from the smoothness lemma (1) and the properness lemma (2) below.
Theorem 5. Equilibria of the two period production model with uncertainty ![]() always exist.
always exist.
Lemma 1 (Smoothness) ![]() is smooth.
is smooth.
Proof. Recall that ![]() is a smooth submanifold of
is a smooth submanifold of![]() . It follows from the definition of a smooth manifold that its natural embedding
. It follows from the definition of a smooth manifold that its natural embedding ![]() is itself smooth. The projection mapping
is itself smooth. The projection mapping ![]() being itself smooth, it follows that
being itself smooth, it follows that ![]() the restriction of the natural projection to
the restriction of the natural projection to ![]() as the composition of two smooth mappings
as the composition of two smooth mappings ![]() is therefore smooth.
is therefore smooth. ![]()
The next lemma makes use of theorem (see [11] , p. 174).
Lemma 2 (Properness) ![]() is proper.
is proper.
Proof. Pick an arbitrary ![]() for
for![]() . Let
. Let ![]() be an element in a compact set
be an element in a compact set![]() . Now, for every
. Now, for every ![]() and
and ![]() need to show (i) that
need to show (i) that ![]() is bounded from below. It follows that
is bounded from below. It follows that
![]()
and by non-satiation have also
![]()
which by monotonicity of ![]() implies that
implies that
![]()
Clearly, there exists some ![]() for every
for every ![]() and
and ![]() satisfying
satisfying
![]()
by boundedness of indifference mappings from below for every![]() . (ii) We now show that for every
. (ii) We now show that for every ![]() and
and![]() ,
, ![]() is also bounded from above. For
is also bounded from above. For ![]() have
have
![]()
where
![]()
Clearly, ![]() , is bounded above by some
, is bounded above by some![]() , since for
, since for![]() ,
, ![]() is bounded from above for every
is bounded from above for every![]() . Hence have established upper and lower bounds defining a compact set
. Hence have established upper and lower bounds defining a compact set
![]()
for every![]() . Let G be a compact set defined by the preimage of the diffeomorphism
. Let G be a compact set defined by the preimage of the diffeomorphism ![]() projected onto
projected onto![]() . Now, by continuity of
. Now, by continuity of![]() ,
, ![]() is closed in
is closed in![]() , which by theorem (2) is a closed subset of
, which by theorem (2) is a closed subset of![]() . Closedness of
. Closedness of ![]() follows from closedness of
follows from closedness of![]() .
. ![]()
The number of equilibria of the long run production model with uncertainty is odd for any regular economy![]() . The modulo 2 degree of
. The modulo 2 degree of ![]() is
is![]() . See Guillemin and Pollack for example [12] .
. See Guillemin and Pollack for example [12] .
I now define a subset of points on ![]() at which pairs
at which pairs ![]() are not regular.
are not regular.
Definition 2. ![]() is the set of singular equilibria
is the set of singular equilibria ![]() given by the singular points of
given by the singular points of![]() .
.
Proposition 1. ![]() is closed.
is closed.
Proof. A necessary and sufficient condition for an equilibrium pair ![]() to be singular is that the determinant of the Jacobian matrix of
to be singular is that the determinant of the Jacobian matrix of![]() , denoted by
, denoted by ![]() is equal to zero. Now, the set of critical points
is equal to zero. Now, the set of critical points ![]() defined by the preimage of
defined by the preimage of ![]() is closed by the closed mapping lemma ([9] ), since
is closed by the closed mapping lemma ([9] ), since![]() ,
, ![]() , and the coefficients of
, and the coefficients of![]() , are all continuous, from which the result follows.
, are all continuous, from which the result follows. ![]()
Definition 3.![]() .
.
A singular value ![]() is the image of
is the image of ![]() of a singular point
of a singular point ![]() into
into![]() . The set of regular values is defined by
. The set of regular values is defined by![]() . It follows that
. It follows that ![]() represents the sets of regular economies. The next proposition states the
represents the sets of regular economies. The next proposition states the ![]() is closed and of measure zero. This means that the probability of observing an economy with this property is “close” to zero. Hence, its complement
is closed and of measure zero. This means that the probability of observing an economy with this property is “close” to zero. Hence, its complement ![]() is an open dense set.
is an open dense set.
Proposition 2. The set of singular economies ![]() is closed and of Lebesgue measure zero in
is closed and of Lebesgue measure zero in![]() .
.
Proof. The proof follows from the application of Sards’s theorem which describes the set of singular values of a smooth mapping having the property of Lebesgue measure zero. Hence know that ![]() is a set of Lebesgue measure zero. Closedness of
is a set of Lebesgue measure zero. Closedness of ![]() follows from the properness of
follows from the properness of![]() .
. ![]()
3. Conclusion
This paper discusses local and global equilibrium properties of a production economy with a long-term time structure. Production is modeled in the demand functions of the consumers. The advantage of this way of modeling production is that it enables us to establish a relationship between production and pure exchange economies. Adding uncertainty to the production model is a further step towards realism. It is shown that the equilibrium set of all production economies with uncertainty has the structure of a smooth submanifold of the Euclidean space which is diffeomorphic to a sphere. These topological properties are of significant economic importance in terms of economic policy design since they imply connectedness and contractability of the set of solutions. It is also shown that the set of singularities of the catastrophe map is closed, and of Lebesuge measure zero. The practical implication of this result is that the probability of observing an economy with a discontinuous price system is close to zero.
NOTES
1Discussion paper: the natural projection approach to smooth production economies, 2011.
![]()
3“Smoothness” follows from the same reasons as in the previous section [8] . It essentially means that all functions are differentiable at any order required.
![]()
5The construction of a Riemanian metric on the equilibrium manifold would be a very useful result towards economic policy analysis.