High-Resolution Broadband Millimeter-Wave Astrophysical Spectrometer with Triple Product Acousto-Optical Processor ()
1. Introduction
Molecular astrophysics, sometimes also called astrochemistry, has a long history. Molecules in space have been studied panchromatically since the discovery of diffuse interstellar bands nearly a century ago in the optical spectral range [1,2]. At UV wavelengths, the spectroscopic capabilities of the Copernicus satellite launched in the early 70s conduced to the detection of molecular rotational transitions of nitrogen, hydrogen and some other more complex molecules including carbon monoxide [3,4]. Almost contemporarily, the first attempts to identify molecules at (sub)-millimeter wavelengths, which is the interval we are particularly interested in, resulted in the detection of CO and CN [5,6].
Molecules are present in virtually every astrophysical scenario: Interstellar, circumstellar and pregalactic gascircumnuclear gas in active galactic nuclei, the atmospheres of stars and planets of the solar system, and very recently in exoplanetary atmospheres [7]. They provide valuable information on gas properties such as excitation, kinematics and chemistry and are amongst the main coolant agents that help on the collapse of primordial material to form galaxies and interstellar clouds to form new stellar generations. While for the analysis of extragalactic objects a rather coarse resolution is enough due to the Doppler broadening (velocity dispersion) of the spectral lines (230 MHz or 300 km/s at 230 GHz), galactic studies require a significantly enhanced resolution, of the order of a few KHz (0.05 km/s).
The construction of (sub)-millimeter spectrometers has been usually based on filter banks and auto-correlators, nevertheless, for a long time it has been recognized the numerous advantages offered by acousto-optic technique, among others, stability, low weight, compactness, and relatively low cost. In fact, these advantages have prompted the construction of acousto-optical spectrometers, not only for a number of earth based and air-borne (sub)-millimeter telescopes [8-11], but also for space missions such as the heterodyne instrument on board of Herschel [12].
So far, nearly 170 circumstellar and interstellar molecular species have been identified, accounting for billions of transitions (vibrational, rotational and electronic) that provide an enormous richness at every spectral band [13]. In connection with these problems of modern molecular astrophysics, the next step can be made in application of the acousto-optical processors to astrophysical radio-wave observations at 1.3 mm (230 GHz). In this paper, we present an advanced conceptual design of a high-bit-rate triple product acousto-optical processor that would complement the near future expected instrumental capabilities of the Large Millimeter Telescope. The Large Millimeter Telescope Alfonso Serrano (GTM-AS/ LMT-AS).
The LMT-AS is a bi-national collaboration between Mexico and the USA, led by the National Institute for Astrophysics, Optics, and Electronics (INAOE) and the University of Massachusetts at Amherst, to construct, commission and operate a 50 m-diameter millimeterwave radio telescope [14]. Construction of the telescope structure is complete at the 4600 m LMT site on the summit of Volcán Sierra Negra (Puebla, Mexico). Firstlight and Early Science observations with the LMT were successfully conducted, respectively, in June-July 2011 and May-July of 2013. Within these observing runs the telescope operated with the inner 32 meter diameter of the antenna and the premier instruments AZTEC, a continuum camera sensitive at 1.1 mm and the Redshift Search Receiver, a spectrometer capable of obtaining spectral images in a wide band (80 - 110 GHz) at a resolution of about 40 MHz. The reader is referred to the LMT webpage (www.lmtgtm.org) for more details on the telescope and its current instrumentation. A third instrument, SEQUOIA, was successfully used at the 14 m antenna of the five college observatory in Massachusetts and is expected to be part of the available instrumentation for the LMT-AS starting in the winter of 2014.
SEQUOIA is a 32-element heterodyne focal plane array receiver for the 85 - 115 GHz frequency band. The system makes use of MMIC (Monolithic Microwave Integrated Circuit) preamplifiers and covers 15 GHz of instantaneous bandwidth. The instrument was used at the FCRAO 14 m antenna between 1998 and 2006 to carry out wide field imaging of molecular line emission in the Milky Way and nearby galaxies [15]. Despite its age, SEQUOIA is still the largest, most sensitive 3 mm focal plane array available today. The instrument will be upgraded in 2014, by replacing the noisiest pixels, and expanding its bandwidth. It is our intent to field the instrument on the 32-m LMT in the winter of 2014, where SEQUOIA will benefit from higher-quality atmospheric conditions, 4 times larger collecting-area (4 times improved surface brightness sensitivity) and 2 times better angular resolution compared to its previous successful observations on the FCRAO 14-m.
Studies of Gassy Disks around Normal Main Sequence Stars
There are numerous astrophysical niches in which a high resolution spectrograph operating within relatively wide frequency bandwidth is a fundamental tool. They are related mainly to the formation of structures as well as stars in their advanced evolutionary stages. The following brief explanation describes one of the most interesting potential applications for similar acousto-optical radio-wave spectrographs.
The global picture in the formation of planetary systems starts with a primordial or protoplanetary disk. Young stellar objects are usually surrounded by material composed of gas and dust. In the very early stages this gas-left over from the original gas cloud that gave rise to star formation-vastly dominates the circumstellar material with only a few percent of the total mass being in the form of dust. As the disk evolves, the gas is removed from the system through several processes, among which, photoevaporation and viscous accretion, leaving the systems dominated by small dust particles that produce the infrared excesses observed in main sequence stars [16,17]. Whilst the gaseous material is expected to be depleted when the star-disk systems is only a few million year old, far less that the stellar ages, there are a few stellar examples in which gas is still present in observable amounts, even for relatively old systems.
The atomic gas component has been optically detected in only a few debris disks, with the most prominent examples being those of the stars Beta-Pictoris and HD- 32297 [18] thanks to the edge-on orientation of the circumstellar material. Molecular gas, on the other side, has been more elusive and has been ascertained in only two systems, 49 Ceti and HD21997, however, in amounts that vastly supersede that of atomic gas, as large as 14 Earth masses for the star 49 Ceti [19,20].
The current debate is whether in these systems, like 49 Ceti, the gas is indeed a residual from the primordial gas that survived the early depletion process or corresponds to a second generation material, in a similar way the dust is thought to be replenished by the collision of planetesimals [21]. The answer to this controversy will certainly come out from sensitive millimeter wave observations at an increased resolution aimed at detecting molecular gas (primarily of CO) that would be eventually complemented with optical observation of atomic gas. To date, there are only a few attempts to find protoplanetary systems similar to 49 Ceti, and the confirmation of the existence of gas and its ubiquity in such systems will await the availability of high-resolution instruments on large aperture facilities such as the Large Millimeter Telescope.
For the special case described above and the more general scenario of star formation, it is necessary to count with a large bandwidth and high resolution, feasible with acousto-optical techniques. As previously indicated, a large bandwidth would allow the inclusion of many molecular species, hence, very valuable tools for constraining the physical properties of the gas. In particular, we propose the application of acousto-optic techniques for the development of a highly productive radio-wave spectrometer with a bandwidth of analysis lying in the gigahertz frequency range together with a spectral resolution belonging to the kilohertz frequency range to work at 1.3 mm (230 GHz). The above-mentioned spectral resolution and frequency bandwidth can be evidently realized by the triple product acousto-optical processor exploiting a space-and time integrating [22]. Such an approach provides the resolution power of about 105 - 106, which makes it possible to investigate not only the intense emission of the carbon monoxide molecule, 12CO (2-1), but also other prominent species such as sulphur dioxide (SO2), cyanoacetylene (C3HN), and others, many of which will be studied for the first time. The expected performances of the radio-wave acousto-optical spectrometer under consideration will be potentially comparable to that of the Atacama Large Millimeter Array (ALMA), and the highest ever achieved in a single dish telescope that will certainly take millimeter wave spectral observations to discovery grounds.
2. Spatially One-Dimensional Acousto-Optical Input Devices
Generally, the systems for optical information processing have an advantage to be three-dimensional in their nature, so that the directions of propagating the corresponding light flows can be usually considered as optical axes. During the propagation of light through each of similar systems, the modulations of light flow by the input data and the other optical transformations can be performed to obtain the desirable issuing light distribution at the output plane of that system. Usually, various modulators, lenses, and other components for optical data processing are located in the planes being orthogonal to that optical axis, so that a two-dimension arrangement makes it possible to carry out a large amount of parallel operations and, in so doing, to achieve potentially ultra-high productivity of processing. Together with this, during the last years a lot of two-dimensional architectures for optical data processing has been progressed, wherein various one-dimensional input devices have been exploited, while these systems as a whole have been designed in a three-dimension space. Realizing two-dimensional optical processors with one-dimensional input devices is not so easy, as a rule; nevertheless, similar systems exhibit a high level of flexibility. As a result, rather large amount of high-quality one-dimensional input devices have been created and inserted into optical systems for two-dimensional data processing in a view of creating high-bit-rate and adaptable optical processors. One of the most important arguments for applying one-dimensional input devices in two-dimensional processing is based on relatively high level of their development. The most widespread of them are, for example, linear arrays of semiconductor light sources like laser diodes or light emission diodes (LEDs); then, one can call a row of electro-optic, acousto-optic, and magneto-optic cells; various CCD linear arrays, etc. It should be noted that modern semiconductor light sources allow effective and ultra-high frequency (up to 1010 Hz) external amplitude modulation, while one-dimensional Bragg acousto-optical cells (AOCs) provide effective conversion of electrical signal into optical ones in a wide (up to a few gigahertz) frequency bandwidth with time-bandwidth product (i.e. a product of the frequency bandwidth and the aperture transit time) exceeding 103. Rather small sizes of similar input devices and modern technique of designing the needed optical lenses give real opportunity for constructing ultra-highproductive and compact optical systems for parallel data processing. Moreover, both relatively low levels of the needed electric power and not high prices inherent in these components lead potentially to realizing compact optical processors of low power consumption as well as of low cost.
In the case of exploiting spatially one-dimensional AOC as an input device, the data can be introduced in a sequential regime. If the signal applied to similar AOC is modulated by the time function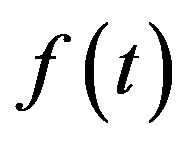 , the light scattered by this cell will be modulated by the function
, the light scattered by this cell will be modulated by the function
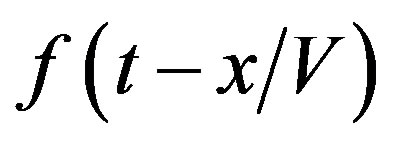 , where
, where  is the coordinate of acoustic wave propagation and V is the acoustic wave velocity. Consequently, at each instant of time
is the coordinate of acoustic wave propagation and V is the acoustic wave velocity. Consequently, at each instant of time , the scattered light is modulated proportionally to the input electric signal with respect to the spatial coordinate x; and together with this, light is modulated by the input electric signal at each individual value of the coordinate
, the scattered light is modulated proportionally to the input electric signal with respect to the spatial coordinate x; and together with this, light is modulated by the input electric signal at each individual value of the coordinate  with respect to the time t. Such a doubled modulation can be important within designing dynamic optical processors, because in the last case the AOC can be exploited as the input devices and as the delay lines. In reality, the modulation provided by AOC is much more complicated process. The scattered light has Doppler frequency shift relative to the initial central frequency, and finite size of the AOC’s aperture always restricts the spatial length of an area wherein the modulation of light beam can be fulfilled. Then, the proportionality between the depth of light modulation and the applied electric signal is true only when diffraction efficiency of the AOC does not exceed a few percent. Additionally, the modulating properties of AOC operating in Bragg regime are essentially depending on the angle of light incidence on a cell. All these factors should be taken into account during the design of practical systems.
with respect to the time t. Such a doubled modulation can be important within designing dynamic optical processors, because in the last case the AOC can be exploited as the input devices and as the delay lines. In reality, the modulation provided by AOC is much more complicated process. The scattered light has Doppler frequency shift relative to the initial central frequency, and finite size of the AOC’s aperture always restricts the spatial length of an area wherein the modulation of light beam can be fulfilled. Then, the proportionality between the depth of light modulation and the applied electric signal is true only when diffraction efficiency of the AOC does not exceed a few percent. Additionally, the modulating properties of AOC operating in Bragg regime are essentially depending on the angle of light incidence on a cell. All these factors should be taken into account during the design of practical systems.
The AOC can be efficiently used as a point modulator as well, because it can provide pure amplitude modulation for the light beam entirely. Within such an application of the AOC, one can imagine that the AOC’s aperture is going to zero, so that space-time signal
 is degenerated into the time function
is degenerated into the time function . If, for example, the AOC is lighted by a conic optical beam focused near the piezoelectric transducer, the scattered optical beam represents almost the same cone modulated with respect to time by the function
. If, for example, the AOC is lighted by a conic optical beam focused near the piezoelectric transducer, the scattered optical beam represents almost the same cone modulated with respect to time by the function . The bandwidth of modulation is inversely proportional to the acoustic transit time through an individual focal spot. For example, with the focal spot size of about
. The bandwidth of modulation is inversely proportional to the acoustic transit time through an individual focal spot. For example, with the focal spot size of about 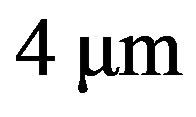 and typical acoustic wave velocity
and typical acoustic wave velocity , the acoustic transit time through that focal spot has the order of
, the acoustic transit time through that focal spot has the order of . It should be noted that with growing the KleinCook parameter [23], which is accompanied by increasing the diffraction efficiency of AOC, the output light cone assumes an elliptic shape due to appearing wave mismatch. Nevertheless, this estimation is rather close to allowable time of direct electronic amplitude modulation for the laser diodes or LEDs. However, sometimes these light sources exhibit the radiation with too low time coherence under action of high-bit-rate modulation. This is why just the AOCs can be efficiently exploited as point modulators providing a wideband time modulation of the light beam as a whole.
. It should be noted that with growing the KleinCook parameter [23], which is accompanied by increasing the diffraction efficiency of AOC, the output light cone assumes an elliptic shape due to appearing wave mismatch. Nevertheless, this estimation is rather close to allowable time of direct electronic amplitude modulation for the laser diodes or LEDs. However, sometimes these light sources exhibit the radiation with too low time coherence under action of high-bit-rate modulation. This is why just the AOCs can be efficiently exploited as point modulators providing a wideband time modulation of the light beam as a whole.
Nevertheless, efficiency of exploiting the third dimension in a three-coordinate space has the decisive significance, because only this property gives potential advantages to optical systems in comparison with the other ones. Consequently, an important question appears: is a two-dimensional data processing system capable of providing rather high productivity under exploitation of just one-dimensional input devices? The adequate answer looks like this: if a one-dimensional input device is involved, some part of the functional possibilities of parallel processing becomes to be lost, because instead of about  resolvable spots of data, provided usually by a spatially two-dimensional light modulator, now only
resolvable spots of data, provided usually by a spatially two-dimensional light modulator, now only 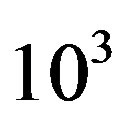 spots can be realized. However, the losses in parallelism can be successfully compensated by very wide frequency bandwidth of already existing one-dimensional input devices. Let us consider a few estimations. The aperture transit time
spots can be realized. However, the losses in parallelism can be successfully compensated by very wide frequency bandwidth of already existing one-dimensional input devices. Let us consider a few estimations. The aperture transit time  of the AOC can be undoubtedly about
of the AOC can be undoubtedly about  (see below) or even more up to
(see below) or even more up to . The frequency bandwidth
. The frequency bandwidth  of similar AOC is usually about
of similar AOC is usually about  or more. Consequently, the time-bandwidth product can be definitely estimated as
or more. Consequently, the time-bandwidth product can be definitely estimated as
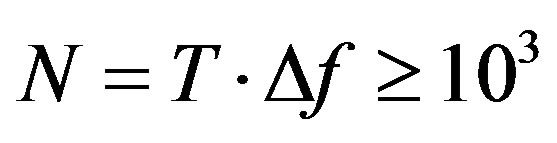 , which represents the number of potentially achievable resolvable spots. This product is almost independent on concrete magnitudes of both
, which represents the number of potentially achievable resolvable spots. This product is almost independent on concrete magnitudes of both  and
and , because it is mainly conditioned by fundamental acousto-optical relations. The direct comparisons of different processors are not always possible, but some estimation can be done. For example, if the AOC with the product
, because it is mainly conditioned by fundamental acousto-optical relations. The direct comparisons of different processors are not always possible, but some estimation can be done. For example, if the AOC with the product  is lighted by the modulated beam from a single-channel source and the frequency bandwidth of this external modulation is taken equal to
is lighted by the modulated beam from a single-channel source and the frequency bandwidth of this external modulation is taken equal to 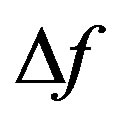 as well, one yields
as well, one yields  of multiplications per second, because during each time interval
of multiplications per second, because during each time interval  one can realize N multiplications. In the case when a pair of similar AOC is located sequentially, the triple-product processor will perform
one can realize N multiplications. In the case when a pair of similar AOC is located sequentially, the triple-product processor will perform  multiplications per second. As a result, using the above-mentioned estimations for the aperture transit time and the frequency bandwidth for the AOC, one can expect the final bit-rate about 1014-15 multiplications per second. Thus, one can conclude that involving one-dimensional input devices with really wide frequency bandwidth in two-dimensional optical gives a chance to create potentially the prototypes of rather highbit-rate optical processors.
multiplications per second. As a result, using the above-mentioned estimations for the aperture transit time and the frequency bandwidth for the AOC, one can expect the final bit-rate about 1014-15 multiplications per second. Thus, one can conclude that involving one-dimensional input devices with really wide frequency bandwidth in two-dimensional optical gives a chance to create potentially the prototypes of rather highbit-rate optical processors.
3. Schemes and Algorithms for Spectrum Analyzers
Let us consider a typical acousto-optical spectrum analyzer depicted in Figure 1(a). The acousto-optical spectrum analyzer includes the laser source of monochromatic light, which is directed to the AOC through the lens  or another collimating optics in such a way that the needed angular requirements are satisfied. In its turn, the AOC is excited by a wide-frequency signal correlated with those angular requirements in the plane
or another collimating optics in such a way that the needed angular requirements are satisfied. In its turn, the AOC is excited by a wide-frequency signal correlated with those angular requirements in the plane . The integrating lens
. The integrating lens  converts the angular spectrum into the linear one and focuses plane waves in an amount of spots lying in its focal plane. The photo-detector is represented by a multi-pixel CCD-linear array, which shapes a discrete video-signal. This scheme allows two extreme options of designing. On the one hand side, the frequency bandwidth is about
converts the angular spectrum into the linear one and focuses plane waves in an amount of spots lying in its focal plane. The photo-detector is represented by a multi-pixel CCD-linear array, which shapes a discrete video-signal. This scheme allows two extreme options of designing. On the one hand side, the frequency bandwidth is about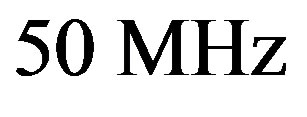 , the processing time is about
, the processing time is about , and the number of parallel channels 1500, while on the other hand, the frequency bandwidth is about
, and the number of parallel channels 1500, while on the other hand, the frequency bandwidth is about , the processing time is about
, the processing time is about , and the number of parallel channels 1000. Usually, performance data inherent in the majority of similar systems lee between these extreme cases with more or less the same time-bandwidth product 1000 - 1500. The number of pixels exceeds usually the time-bandwidth product by
, and the number of parallel channels 1000. Usually, performance data inherent in the majority of similar systems lee between these extreme cases with more or less the same time-bandwidth product 1000 - 1500. The number of pixels exceeds usually the time-bandwidth product by
 (a)
(a) (b)
(b)
Figure 1. Optical layouts of the acousto-optic spectrum analyzers with the space integration (a) and for the chirp Z-transform (b).
2 - 3 times to provide the needed discreteness of a spectrum under analysis. Because of each doublet or maybe triplet of pixels is equivalent to a single frequency channel, the CCD-linear arrays have usually from 1024 to 4096 pixels, and the expected number of frequency channels can be really large, the advantages of acoustooptical spectrum analyzers can be easily estimated. Natural parallelism inherent in the optical system illustrates potential superiority of the acousto-optics in comparison with electronics in this area. During the operation of acousto-optical spectrum analyzer lighting the AOC is almost perpendicular to its input optical facet, and together with this the piezoelectric transducer of that AOC is exited by an external electronic signal , so that the light wave signal at the output facet can be finally represented as
, so that the light wave signal at the output facet can be finally represented as . The lens
. The lens  provides the Fourier transform
provides the Fourier transform 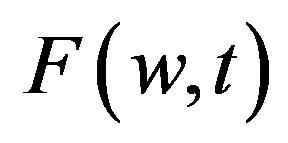 in the plane
in the plane , where
, where
 , (1)
, (1)
where the space frequency 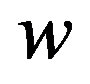 is connected with the physical coordinate
is connected with the physical coordinate  in the plane
in the plane  and the focal distance
and the focal distance  of the integrating lens
of the integrating lens  as
as
 . In fact, the integration limits are constrained by the aperture of the AOC. Because of integration in Equation (1) is performed with respect of the space coordinate at the input plane of a cell, one can say that this analyzer belongs to a group of architectures with the space integrating.
. In fact, the integration limits are constrained by the aperture of the AOC. Because of integration in Equation (1) is performed with respect of the space coordinate at the input plane of a cell, one can say that this analyzer belongs to a group of architectures with the space integrating.
The ability to resolve signals in the frequency domain is oriented on fixing the gap of a pre-scripted depth between two frequencies in the Fourier domain. Moreover, the reasons for this capability are connected with the Rayleigh criterion for resolution within determining the angular distance between stars using a telescope. The Rayleigh criterion is based on the uniformity of lighting the telescope aperture, so that light intensity in the image plane is described by the squared sinc-function. In so doing, the gap of a 1-dB-depth can be obtained with a peak magnitude for one frequency component coincides with the first zero for the neighboring frequency component. The gap of such a depth is well seen visually as well as on a photo-film. Applying the Rayleigh criterion to the acousto-optical spectrum analyzer, one can find that the spatial distance  between two neighboring frequency components in the focal plane of the integrating lens
between two neighboring frequency components in the focal plane of the integrating lens 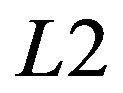 can be estimated as
can be estimated as
 , where
, where  is the focal distance of the lens
is the focal distance of the lens ,
,  is the aperture of the AOC,
is the aperture of the AOC, 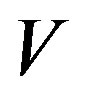 is the acoustic velocity, and
is the acoustic velocity, and  is the frequency resolution. These equalities give us
is the frequency resolution. These equalities give us
 . Moreover, one can apply various techniques for the incident light apodization to detect definitely weak signals. However, the suppressing of side lobes can be achieved at the expense of the corresponding demerit in the frequency resolution.
. Moreover, one can apply various techniques for the incident light apodization to detect definitely weak signals. However, the suppressing of side lobes can be achieved at the expense of the corresponding demerit in the frequency resolution.
The other algorithm for spectrum analysis can be based on the time integration and the chirp Z-transform is a method, which is often exploited for performing the Fourier transform in systems where only the time variable is available. The chirp Z-transform is based on the fact that the factor 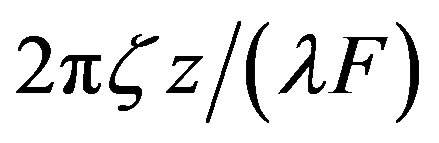 in the kernel of Fourier transform is equal to
in the kernel of Fourier transform is equal to
 . The equivalent way for explaining the Fourier-transform determined by Equation (1) gives
. The equivalent way for explaining the Fourier-transform determined by Equation (1) gives
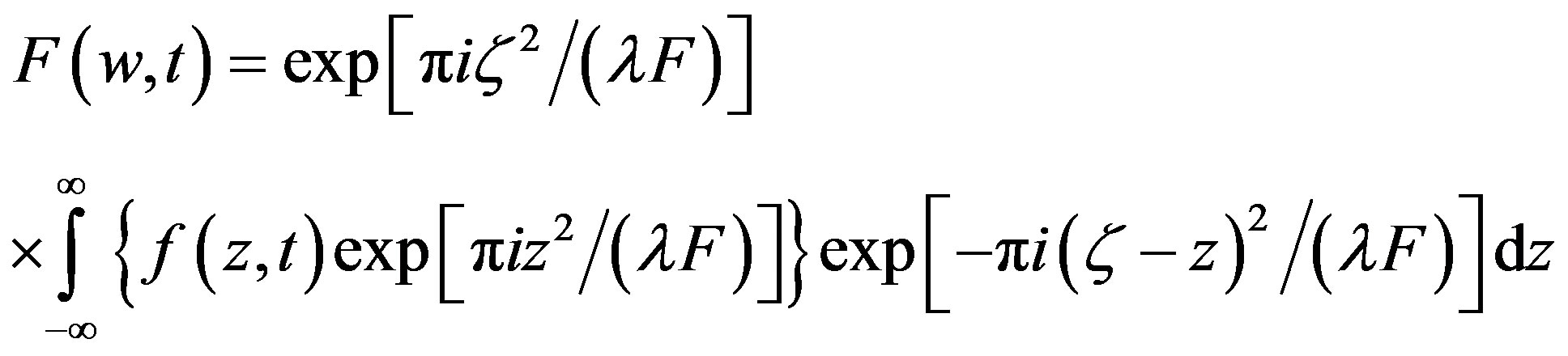 (2)
(2)
This formula demonstrates that at first the optical signal  at the input facet is multiplied by the factor
at the input facet is multiplied by the factor
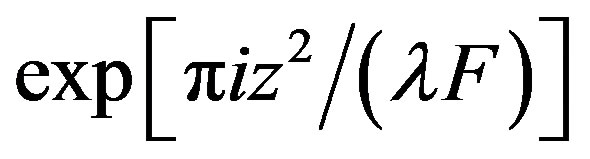 . Then, the Fresnel transform of the obtained product is fulfilled, and finally the result of integration is multiplied by the factor
. Then, the Fresnel transform of the obtained product is fulfilled, and finally the result of integration is multiplied by the factor 
to compensate a square-law phase factor. The Fresnel transform in optics means that a light beam with some space distribution is propagating at a distance  in free space. In principle, it is a physical phenomenon accompanied by a diffraction when the angle of light diffraction is linearly dependent on both time and space frequencies at the input. Figure 1(b) represents a configuration for an optical system capable of performing the chirp Z-transform. Thus one can see its analogy with the Fouriertransform system depicted in Figure 1(a); their only difference consist in the positions of lenses. The lens
in free space. In principle, it is a physical phenomenon accompanied by a diffraction when the angle of light diffraction is linearly dependent on both time and space frequencies at the input. Figure 1(b) represents a configuration for an optical system capable of performing the chirp Z-transform. Thus one can see its analogy with the Fouriertransform system depicted in Figure 1(a); their only difference consist in the positions of lenses. The lens  lights an external electronic signal
lights an external electronic signal  by coherent light beam, providing its pre-multiplication by the factor
by coherent light beam, providing its pre-multiplication by the factor . The resulting beam propagation in free space does the operation of integral convolution, while the lens
. The resulting beam propagation in free space does the operation of integral convolution, while the lens  gives us the needed post-multiplication by the factor
gives us the needed post-multiplication by the factor . Application of the chirp Z-transform to various system architectures provides their significant flexibility relative to both the frequency resolution and the frequency bandwidth for analysis as well as makes it possible to design spectrum analyzers with the time integration, which have considerably improved frequency resolution.
. Application of the chirp Z-transform to various system architectures provides their significant flexibility relative to both the frequency resolution and the frequency bandwidth for analysis as well as makes it possible to design spectrum analyzers with the time integration, which have considerably improved frequency resolution.
4. A Triple-Product Acousto-Optical Processor
The technique of signal processing based on the spaceand-time-integrating had been proposed for the spectrum analysis of one-dimensional signals [24,25]. In principle, the analysis of one-dimensional signals can be provided by one-dimensional acousto-optical analyzer with only the spaceor only the time-integrating. However, these analyzers have the performances supplementing with one another. The space-integrating gives a wide frequency bandwidth together with relatively low frequency resolution, while the time-integrating provides a high resolution for spectrum components accompanied by comparably narrow frequency bandwidth. A two-dimensional processor combining the advantages from both spaceand time-integrating makes it possible to obtain the analysis with wide bandwidth as well as high resolution simultaneously. A scheme of the space-and-time integrating spectrum analyzer exploiting a pair of the acousto-optical cells (AOCs) is shown in Figure 2. The triple product acousto-optical processor applies the algorithm of the space-and-time integrating, which provides rather wideband studies with an up rated spectral resolution. This processor includes a pair of mutually orthogonally oriented wide-aperture 1D-acousto-optic cells as the input devices for a 2D-optical spectrum analysis. Significance of this approach is conditioned by the usage of the above-noted chirp Z-transform technique realizing a 2D-Fourier transform of the input signal  [26, 27].
[26, 27].
The laser diode or LED, for example, can be used as a point light source whose radiation is modulated in time by the initial electronic signal . The vertically
. The vertically

Figure 2. Schematic arrangement for a triple-product acousto-optical processor.
oriented acousto-optic cell AOC-1 does a modulation by the first additional electronic signal . This cell is lighted by the optical beam from a point source through the spherical lens
. This cell is lighted by the optical beam from a point source through the spherical lens  and the cylindrical lens
and the cylindrical lens . The light beam, scattered by the AOC-1, is modulated by the product
. The light beam, scattered by the AOC-1, is modulated by the product . In a view of lighting the AOC-2, which is placed horizontally, the output light beam after the AOC-1 is broadened horizontally and focused vertically by the spherical lens
. In a view of lighting the AOC-2, which is placed horizontally, the output light beam after the AOC-1 is broadened horizontally and focused vertically by the spherical lens . Let the second additional electronic signal, which is applied to the AOC-2, be
. Let the second additional electronic signal, which is applied to the AOC-2, be . As a result, the light beam, scattered by the AOC-1, is modulated by the triple product
. As a result, the light beam, scattered by the AOC-1, is modulated by the triple product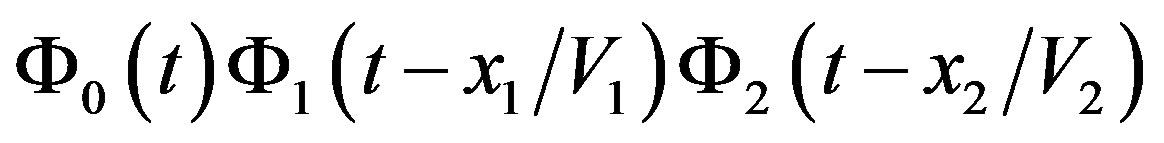 . The obtained result includes in fact two time delays
. The obtained result includes in fact two time delays  and
and
 , where
, where  and
and  are physical spatial coordinates along the corresponding acousto-optical cells and the acoustic wave velocities, respectively. These time delays
are physical spatial coordinates along the corresponding acousto-optical cells and the acoustic wave velocities, respectively. These time delays  and
and  must satisfy the inequality
must satisfy the inequality , where the aperture transit time
, where the aperture transit time  of the modern acousto-optical cells can be equal to about
of the modern acousto-optical cells can be equal to about . The cylindrical lens
. The cylindrical lens  and the spherical lens
and the spherical lens 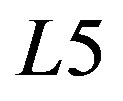 shape the image of the AOC-2 at the output plane in horizontal direction, while the spherical lenses
shape the image of the AOC-2 at the output plane in horizontal direction, while the spherical lenses  and
and  give the image of the AOC-1 at the output plane in vertical direction. A two-dimensional matrix of photo-detectors is placed in the output plane, so that charges
give the image of the AOC-1 at the output plane in vertical direction. A two-dimensional matrix of photo-detectors is placed in the output plane, so that charges  collected by each individual pixel under acting the light during the time
collected by each individual pixel under acting the light during the time  at a point
at a point 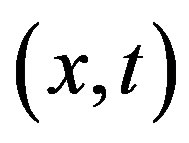 are proportional to
are proportional to
 , (3)
, (3)
where  is the time of integration, which is limited by the detector and could be about
is the time of integration, which is limited by the detector and could be about 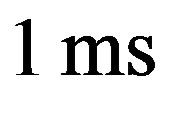 or more; the time delays
or more; the time delays  and
and  represent a pair of the coordinates in the output focal plane, i.e. in a plane of the CCD matrix photo-detector. Such a system represents a triple-product processor. However, the system does not simply collect two one-dimensional conversions; the final result appears within a joint two-dimensional processing of all the input signals. This architecture always calculates Equation (3), but it exhibits really high flexibility, because all the three input signals are given initially as electronic signals. In this way the processor can be easily re-oriented from fulfilling one algorithm to another in the frames of completely the same optical resources simply by varying the input electronic signals
represent a pair of the coordinates in the output focal plane, i.e. in a plane of the CCD matrix photo-detector. Such a system represents a triple-product processor. However, the system does not simply collect two one-dimensional conversions; the final result appears within a joint two-dimensional processing of all the input signals. This architecture always calculates Equation (3), but it exhibits really high flexibility, because all the three input signals are given initially as electronic signals. In this way the processor can be easily re-oriented from fulfilling one algorithm to another in the frames of completely the same optical resources simply by varying the input electronic signals 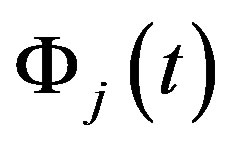 with
with .
.
5. Brief Description of Potential Advantages Peculiar to the Space-and-Time Integrating Processor
Let us apply algorithm of the above-mentioned chirp-  transform technique to processing the signal
transform technique to processing the signal . That technique involves two frequency-chirp signals whose parameters
. That technique involves two frequency-chirp signals whose parameters  and
and  represent the frequency variables along the output axes
represent the frequency variables along the output axes 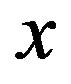 and
and  (
(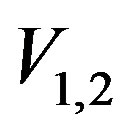 are the acoustic velocities as before). In so doing, one can take, for example:
are the acoustic velocities as before). In so doing, one can take, for example: ,
,
 ,
,  and
and . As a result the output function will have the form:
. As a result the output function will have the form:
 (4)
(4)
Without the square-law phase term, the function  can be considered as the Fourier-transform of the signal
can be considered as the Fourier-transform of the signal , which has been calculated using the algorithm of chirp-Z-transform with respect to both the space coordinates, so that spectrum of the signal
, which has been calculated using the algorithm of chirp-Z-transform with respect to both the space coordinates, so that spectrum of the signal 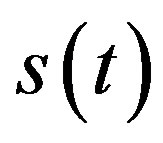 will be displayed along the coordinates
will be displayed along the coordinates  and
and . Maximal frequencies for the spectrum inherent in the signal
. Maximal frequencies for the spectrum inherent in the signal , and presented along the axes
, and presented along the axes  and
and , are equal to
, are equal to  and
and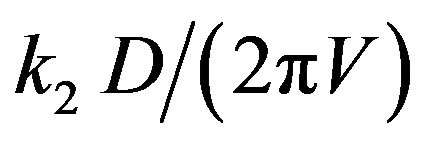 , where
, where  is the apertures of both the AOCs. If the factor
is the apertures of both the AOCs. If the factor  is chosen in such a way that
is chosen in such a way that  is the bandwidth of the signal
is the bandwidth of the signal , the complete frequency spectrum of this signal will be registered and represented along the axis
, the complete frequency spectrum of this signal will be registered and represented along the axis  with relatively low frequency resolution corresponding to the conventional space integration spectrum analysis. This estimation is conditioned by the fact that resolution is determined by the ratio of the frequency bandwidth
with relatively low frequency resolution corresponding to the conventional space integration spectrum analysis. This estimation is conditioned by the fact that resolution is determined by the ratio of the frequency bandwidth 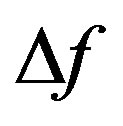 to the number
to the number  of pixels peculiar to the taken
of pixels peculiar to the taken  CCD-matrix along the axis
CCD-matrix along the axis , i.e. the frequency resolution is characterized by the value
, i.e. the frequency resolution is characterized by the value . Additionally, if the factor
. Additionally, if the factor  is selected as
is selected as , one has arrived at the case when only a
, one has arrived at the case when only a  -part of a spectrum will be depicted along the axis
-part of a spectrum will be depicted along the axis  for each individual position along the axis
for each individual position along the axis . As a result, the frequency resolution along the axis
. As a result, the frequency resolution along the axis 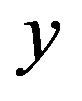 becomes to be equal to the value
becomes to be equal to the value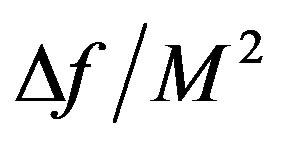 . These estimations are true under condition that the time of integration
. These estimations are true under condition that the time of integration  exceeds
exceeds . A combination of the transformation along the axis
. A combination of the transformation along the axis  with relatively low resolution in a wide frequency bandwidth with the transformation along the axis
with relatively low resolution in a wide frequency bandwidth with the transformation along the axis 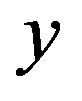 with a high frequency resolution, but in a narrow frequency bandwidth represents a two-dimensional folded spectrum. Such a spectrum gives a two-dimensional raster for recording
with a high frequency resolution, but in a narrow frequency bandwidth represents a two-dimensional folded spectrum. Such a spectrum gives a two-dimensional raster for recording  counts of one-dimensional Fourier-images of the signal
counts of one-dimensional Fourier-images of the signal . Shaping a onedimensional spectrum along a pair of space coordinates within this architecture makes it possible to display up to
. Shaping a onedimensional spectrum along a pair of space coordinates within this architecture makes it possible to display up to  spectrum components, because the matrix of photodetectors has
spectrum components, because the matrix of photodetectors has 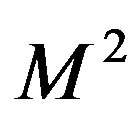 pixels. Thus, this technique provides potentially a high frequency resolution together with rather wide frequency bandwidth of the spectrum analysis. Finally, this processor produces the resultant folded spectrum, which is subject to electronic post-processing. Generally, this technique accumulates the principal advantages of both space and time integrating acousto-optical processors. In particular, with the typical value of
pixels. Thus, this technique provides potentially a high frequency resolution together with rather wide frequency bandwidth of the spectrum analysis. Finally, this processor produces the resultant folded spectrum, which is subject to electronic post-processing. Generally, this technique accumulates the principal advantages of both space and time integrating acousto-optical processors. In particular, with the typical value of , similar system exhibits rather wide frequency bandwidth
, similar system exhibits rather wide frequency bandwidth , which is practically equal to bandwidth of the input piezoelectric transducers of acousto-optical cells. Broadly speaking, the magnitude of
, which is practically equal to bandwidth of the input piezoelectric transducers of acousto-optical cells. Broadly speaking, the magnitude of 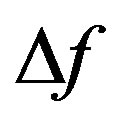 can be estimated from
can be estimated from  to more than
to more than  in modern acousto-optics. Together with this, similar system is able to provide a high frequency resolution
in modern acousto-optics. Together with this, similar system is able to provide a high frequency resolution , which is practically equal to the reciprocal of the CCD-matrix photo-detector integration time
, which is practically equal to the reciprocal of the CCD-matrix photo-detector integration time . Within optimal choosing of both the integration time
. Within optimal choosing of both the integration time  and the abovenoted factors
and the abovenoted factors  inherent in a pair of the frequencychirp signals, one can vary the needed frequency resolution
inherent in a pair of the frequencychirp signals, one can vary the needed frequency resolution  from about 10 Hz to 10 KHz.
from about 10 Hz to 10 KHz.
6. Schematic Arrangement and Current Design
One of the allowable practical arrangements of the above-characterized optical scheme for the triple-product acousto-optical processor is presented as a simplified prototype in Figures 3 and 4 (some optical components are not shown in this figures). The scheme is based on an advanced 3-inch components, i.e. for a spectrum analyzer with the space-and-time integrating, depicted in Figure 2. The designed arrangement is localized on a  -feet optical breadboard and based on specifically selected and optimized set of three-inch spherical and cylindrical lenses. The semiconductor laser, allowing an external amplitude modulation with the frequency up to 3 GHz can be potentially chosen as a point source of light because its light output is arranged through a connector with a span of the single mode optical fiber.
-feet optical breadboard and based on specifically selected and optimized set of three-inch spherical and cylindrical lenses. The semiconductor laser, allowing an external amplitude modulation with the frequency up to 3 GHz can be potentially chosen as a point source of light because its light output is arranged through a connector with a span of the single mode optical fiber.
The selected optical and mechanical components make it possible to use of highly effective and specially designed wide-aperture AOCs. For this purpose, in particular, let us take a few spatially one-channel crystalline AOCs. For example, in the case of relatively low frequencies of analysis one can consider a tellurium dioxide  crystalline cell from Molecular Technology GmbH, see Figure 5. It has the access time
crystalline cell from Molecular Technology GmbH, see Figure 5. It has the access time ,
,

Figure 3. Layout of the simplified optical scheme for the acousto-optical triple-product processor.

Figure 4. Potential simplified design of a prototype for the triple-product acousto-optical processor.

Figure 5. A TeO2-crystal based AOC. (Molecular Technology GmbH).
optical aperture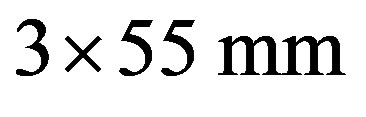 , diffraction efficiency > 65%, and frequency bandwidth
, diffraction efficiency > 65%, and frequency bandwidth  at the carrier frequency
at the carrier frequency , so that its time-bandwidth product [28] is about 4250. Together with this, one can mention high frequency AOCs mode of lithium niobate
, so that its time-bandwidth product [28] is about 4250. Together with this, one can mention high frequency AOCs mode of lithium niobate 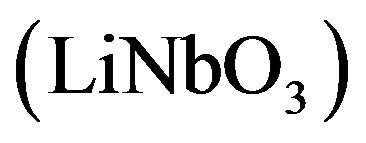 and rutile
and rutile  crystals [29,30]. These AOCs operate in the gigahertz range up to
crystals [29,30]. These AOCs operate in the gigahertz range up to  providing the frequency bandwidth of about
providing the frequency bandwidth of about  per one spatial channel. Their optical apertures and time-bandwidth products are mainly limited by total acoustical losses accessible per aperture for the chosen acoustical mode and the technology selected for producing the needed piezo-electric transducers.
per one spatial channel. Their optical apertures and time-bandwidth products are mainly limited by total acoustical losses accessible per aperture for the chosen acoustical mode and the technology selected for producing the needed piezo-electric transducers.
Then, the CCD matrix camera EO-5023M (Edmund Optics) can be potentially considered as the time-integrating multi-pixel (more than  pixels of 3.45 × 3.45
pixels of 3.45 × 3.45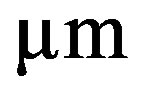 ) photo-detector due to its 12-bit pixel depth and up to 60 s exposure time. This camera with the sensing area 8.45 × 7.07 mm is presented in Figure 6.
) photo-detector due to its 12-bit pixel depth and up to 60 s exposure time. This camera with the sensing area 8.45 × 7.07 mm is presented in Figure 6.
7. Conclusions
The current state of designing a high-bit-rate triple product processor has been presented. The main goal is to create an advanced acousto-optical radio-wave spectrometer for application to the molecular astrophysics. The above-presented consideration of a few key aspects related to creating an optical scheme of the processor reflects an indispensable step for the practical design of

Figure 6. The CCD matrix camera EO-5023M (Edmund Optics).
similar radio-wave spectrometer. The acousto-optical processor under construction will be able to carry out the algorithm of the space-and-time integrating.
This capability is desirable for the simultaneous analysis of a wideband spectrum of radio-wave signals and the improved resolution power, expected to be about  for operations at 1.3 mm (230 GHz). A reasonable part of the performed analysis has been devoted to practical design of the schematic arrangement currently based on three-inch optics and wide-aperture spatially one-channel AOCs as the input devices for a 2Doptical data processing. Various 1D-acousto-optical cells made of the tellurium dioxide
for operations at 1.3 mm (230 GHz). A reasonable part of the performed analysis has been devoted to practical design of the schematic arrangement currently based on three-inch optics and wide-aperture spatially one-channel AOCs as the input devices for a 2Doptical data processing. Various 1D-acousto-optical cells made of the tellurium dioxide , lithium niobate
, lithium niobate , and rutile
, and rutile  crystals have been briefly mentioned together with the CCD-matrix specifically oriented to an increased exposure time, i.e. to the enlarged integration time. Undoubtedly, developing such a highly productive radio-wave spectral instrument promises both appreciable progresses in the technique of precise observations associated with pioneering results in modern molecular astrophysics.
crystals have been briefly mentioned together with the CCD-matrix specifically oriented to an increased exposure time, i.e. to the enlarged integration time. Undoubtedly, developing such a highly productive radio-wave spectral instrument promises both appreciable progresses in the technique of precise observations associated with pioneering results in modern molecular astrophysics.
8. Acknowledgements
This work has been financially supported through the CONACyT Grants # 134085 and # 151494.