Speed kills: Highly relativistic spaceflight would be fatal for passengers and instruments ()
1. INTRODUCTION
Stories, books and movies about space travel often describe journeys at near-light velocities [e.g. refs [1-3]]. Such high speed is desirable as the resulting relativistic time dilation reduces the subjective duration of the trip [4] so that travelers can live long enough to reach their destination. The relativistic rocket equation shows the enormous difficulty of achieving such velocities [5,6].
Interstellar H [7,8], although only present on average at a density of approximately 1.8 H atoms per cm3 [9], turns into deadly radiation [6] as spaceship velocities approach the speed of light. In addition, the energy loss of ionizing radiation passing through the ship’s hull represents an increasing heat load [5] that necessitates large expenditures of energy to cool the ship’s hull. Stopping this flux with either material or electromagnetic shields appears to be very difficult.
The effects of H-atom radiation and heating are formidable obstacles to efficient relativistic interstellar travel by people or even instrumented exploratory vessels. Yet they are not generally treated in courses or books on relativity or the physics of space travel (e.g. refs [2,10,11]).
We consider trips over distances in which cosmological expansion is not significant, e.g. within our galaxy. Then we can define a “space rest frame” which contains the trip origin and destination, and suppose that the ship is moving at velocity v relative to the space rest frame. In the space-rest frame, we assume that interstellar H atoms have small, nonrelativistic thermal velocities that we can say are approximately zero.
2. THE SHIP
For our analysis we assume a 10 m diameter spherical vessel with 0.10 m thick aluminum outer hull. This thickness is within the range of shielding that has been considered for interplanetary travel within the solar system [12]. The weight of this vessel wall would be approximately 85 metric tons (tonne).
3. RELATIVISTIC TIME DILATION/SPACE COMPRESSION
Time for the travelers is slowed by the relativistic dilation factor [4]
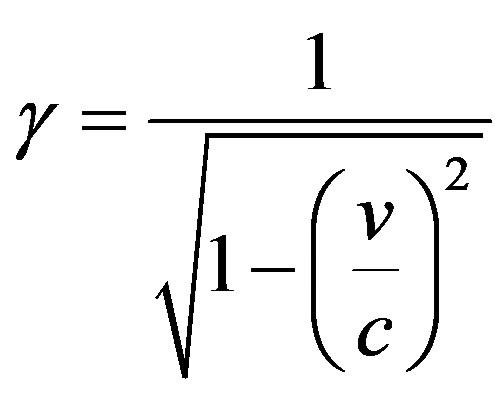
(1)
where v is the spacecraft velocity and c is the speed of light. So a trip that takes time T to an external observer will have subjective duration T/
to a traveler. 
is also the factor by which space is compressed from the travelers’ viewpoint and therefore represents an increase in the density of the incident H flux.
4. HOW FAR, HOW FAST?
Our galaxy has a diameter of about 100,000 light years. Voyager 1, now headed out of the solar system, is traveling at 17 km/s (38,000 mph). At that speed it would take about 75,000 years to go as far as the Alpha Centauri star group, our closest stellar neighbors [13,14]. Thus present rocket technology is not going to get us very far very fast in exploring the galaxy.
Our sun is approximately 25,000 light years from the galactic center [15], and it takes light 25,000 years to go that far. Suppose a traveler would like to make a trip of this distance in a reasonable personal (proper) time. Then he or she would have to travel at a velocity which gives 
= several thousand. An efficient way to travel a distance d in reasonably comfortable fashion is to accelerate at 1g for the first d/2 (in this case, 12,500 light years) and decelerate at 1g for the second half. Using the kinematic equations for relativistic spaceflight [5] (reproduced in our Appendix for reference), the ship achieves a peak
. This trip takes 19.7 years personal time for the passengers and 25,002 years for the people back on earth.
5. H PARTICLE FLUX AND ENERGY
Interstellar atomic H was detected in 1951 from its radio signal [7,8]. Its average density is about 1.8 atoms/cm3 and varies from about 20 atoms/cm3 in diffuse clouds to 0.1 atoms/cm3 between clouds [9].
As the ship’s speed increases, so does the apparent energy of the incident H atoms, whose separated protons and electrons then penetrate the ship’s hull and irradiate the travelers and ship’s instruments.
The flux of H atoms can be calculated from the viewpoint of the ship rest frame. When it is traveling through the galaxy at velocity ≈ c, in its rest frame it is subject to a flux Φ of H atoms
(2)
Where
is the relativistic time dilation/space compression factor defined in Eq. 1.
Thus as the ship approaches the speed of light, the energy and the flux of the incident particles both increase in a steeply nonlinear manner.
The incoming H atoms are separated into protons and electrons as soon as they encounter the hull and then become streams of separated protons and electrons.
The incident protons have rest energy mpc2 = 0.94 GEV (giga (109) electron volts), where 1 eV (electron volt) is the energy gained by a unit charged particle traversing a voltage difference of 1 volt,
.
The total energy 
of the incident protons is therefore [4]
(3)
The kinetic energy 
of a single proton is
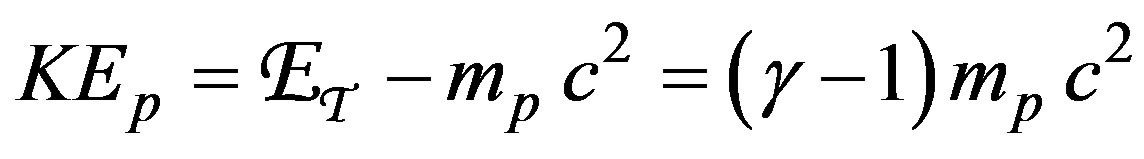(4)
The total energy and kinetic energy of the electrons in the H atoms are given by the same formulas but with the electron rest energy 
(mega (106) electron volts).
Table 1 shows the kinetic energy for protons and electrons as a function of ship velocity.
6. IRRADIATION AND RADIATION DOSE
6.1. Protons
Figure 27.2 in Bichsel et al. [16] shows the energy loss for protons with energy up to about 10,000 GeV passing through various materials. For 
proton kinetic energy ≥ 390 MeV, the energy loss across a range of materials is approximately