1. Introduction
The concept of entropy was founded by Shannon [1] in 1949, which is a measurement of the degree of uncertainty of random variables. In 1972, De Luca and Termini [2] introduced the definition of fuzzy entropy by using Shannon function. Inspired by the Shannon entropy and fuzzy entropy, Liu [3] in 2009 proposed the concept of entropy of uncertain variable, where the entropy characterizes the uncertainty of uncertain variable resulting from information deficiency.
Tsallis Entropy initiated by Tsallis [4-6] in 1988, this is based on the following single parameter generalization of the Shannon entropy:

where  is a conventional positive constant, which is usually set equal to 1,
is a conventional positive constant, which is usually set equal to 1,  is the total number of microsopic configurations, and
is the total number of microsopic configurations, and  is the set of associated probabilities
is the set of associated probabilities . For the equiprobability distribution
. For the equiprobability distribution , the value of Tsallis entropy
, the value of Tsallis entropy , where
, where  is a monotonic increasing function of
is a monotonic increasing function of ,
,  is a real number. It is clearly that in the limit
is a real number. It is clearly that in the limit ,
,  recovers the Shannon entropy formula:
recovers the Shannon entropy formula:

Henceforth, many scholars conduct to research the tsallis entropy, such as S. Abe [7], S. Abe and Y. Okamoto [8], R. J. V. dos Santos [9] and so on.
Uncertainty theory was founded by Liu [10] in 2007 and refined by Liu [11] in 2010, which is a branch of mathematics based on normality, monotonicity, selfduality, countable subadditivity, and product measure axioms. It is a effectively mathematical tool disposing of imprecise quantities in human systems. In recent years, Uncertainty theory was widely developed in many disciplines, such as uncertain process [12], uncertain calculus [3], uncertain differential equation [3], uncertain logic [13], uncertain inference [14], uncertain risk analysis [15], and uncertain statistics [11]. Meanwhile, Liu [16] proposed a spectrum of uncertain programming and applied it into system reliability design, facility location problems, vehicle routing problems, project scheduling problems and so on.
In order to provide a quantitative measurement of the degree of uncertainty in relation to an uncertain variable, Liu [3] proposed the definition of uncertain entropy resulting from information deficiency. Dai and Chen [17] investigated the properties of entropy of function of uncertain variables. The principle of maximum entropy for uncertain variables are introduced by Chen and Dai [18]. Besides, there are many literature concerning the definition of entropy of uncertain variables, such as Chen [19], Dai [20], etc.
Inspired by the tsallis entropy, this paper introduces a new type of entropy, single parameter entropy in the framework of uncertain theory and discusses its properties. Consequently, we generalize the entropy of uncertain variable. The rest of the paper is organized as follows. In Section 2, we recall some basic concepts and theorems of uncertain theory. In Section 3, the definition of single parameter entropy of uncertain variables is proposed. In addition, some examples of the single parameter entropy are illustrated. In Section 4, several properties of single parameter entropy are proved. In Section 5, gives some discussions of single parameter entropy. In Section 6, some examples of single parameter entropy are given. At last, a brief summary is drawn.
2. Preliminaries
In this section, we will recall several basic concepts and theorems in the uncertain theory.
Let  be a nonempty set, and
be a nonempty set, and  a
a  -algebra over
-algebra over . Each element
. Each element 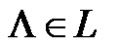 is called an event. Uncertain measure
is called an event. Uncertain measure  was introduced as a set function satisfying the following five axioms ([10]):
was introduced as a set function satisfying the following five axioms ([10]):
Axiom 1. (Normality Axiom)  for the universal set
for the universal set .
.
Axiom 2. (Monotonicity Axiom)  whenever
whenever .
.
Axiom 3. (Self-Duality Axiom)  for any event
for any event .
.
Axiom 4. (Countable Subadditivity Axiom) For every countable sequence of events , we have
, we have
 .
.
Axiom 5. (Product Measure Axiom) Let  be nonempty sets on which
be nonempty sets on which  are uncertain measures
are uncertain measures , respectively. Then the product uncertain measure
, respectively. Then the product uncertain measure  is an uncertain measure on the product
is an uncertain measure on the product  -algebra
-algebra  satisfying
satisfying
 .
.
where .
.
We will introduce the definitions of uncertain variable and uncertainty distribution as follows.
Definition 2.1 (Liu [10]) Let  be a nonempty set, and
be a nonempty set, and  be a
be a 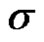 -algebra over
-algebra over , and
, and  an uncertain measure. Then the triplet
an uncertain measure. Then the triplet  is called an uncertainty space.
is called an uncertainty space.
Definition 2.2 (Liu [10]) An uncertain variable is a measurable function from an uncertainty space 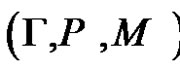 to the set of real numbers.
to the set of real numbers.
Definition 2.3 (Liu [10]) The uncertainty distribution  of an uncertain variable
of an uncertain variable  is defined by
is defined by
 .
.
Theorem 2.1 (Sufficient and Necessary Condition for Uncertainty distribution [21]) A function  is an uncertainty distribution if and only if it is an increasing function except
is an uncertainty distribution if and only if it is an increasing function except  and
and .
.
Example 2.1 An uncertain variable  is called normal if it has a normal uncertainty distribution
is called normal if it has a normal uncertainty distribution

denoted by  where
where  and
and  are real numbers with
are real numbers with .
.
Then we will recall the definition of inverse uncertainty distribution as follows.
Definition 2.4 (Liu [11]) An uncertainty distribution 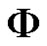 is said to be regular if its inverse function
is said to be regular if its inverse function  exists and is unique for each
exists and is unique for each .
.
Definition 2.5 (Liu [11]) Let  be an uncertain variable with uncertainty distribution
be an uncertain variable with uncertainty distribution . Then inverse function
. Then inverse function  is called the inverse uncertainty distribution of
is called the inverse uncertainty distribution of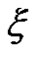 .
.
Example 2.2 The inverse uncertainty distribution of normal uncertain variable 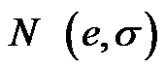 is
is
 .
.
Definition 2.6 (Independence of uncertain variable Liu [10]) The uncertain variables  are said to be independent if
are said to be independent if
 .
.
for any Borel sets  of real numbers.
of real numbers.
Example 2.3 Let  and
and  be independent normal uncertain variables
be independent normal uncertain variables  and
and , respectively. Then the sum
, respectively. Then the sum  is also normal uncertain variable
is also normal uncertain variable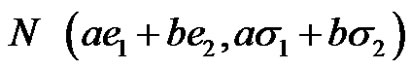 for any real number
for any real number  and
and .
.
Finally we will recall their theorems about the operational law of independent uncertain variables.
Theorem 2.2 (Liu [11]) Let  be independent uncertain variables with uncertainty distribution
be independent uncertain variables with uncertainty distribution , respectively. If
, respectively. If 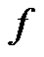 be a strictly increasing with respect to
be a strictly increasing with respect to  and strictly decreasing with respect to
and strictly decreasing with respect to . Then
. Then
 is an uncertain variable with inverse uncertain distribution
is an uncertain variable with inverse uncertain distribution
 .
.
Example 2.4 Let  and
and 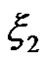 be independent and positive uncertain variables with uncertainty distribution
be independent and positive uncertain variables with uncertainty distribution  and
and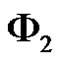 , respectively. Then the inverse uncertainty distribution of the quotient
, respectively. Then the inverse uncertainty distribution of the quotient  is
is
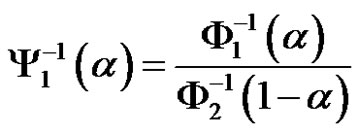 .
.
3. Single Parameter Entropy
In this section, we will introduce the definition and theorem of single parameter entropy of uncertain variable. For the purpose, we recall the entropy of uncertain variable proposed by Liu [3].
Definition 3.1 (Liu [3]) Suppose that  is an uncertain variable with uncertainty distribution
is an uncertain variable with uncertainty distribution . Then its entropy is defined by
. Then its entropy is defined by
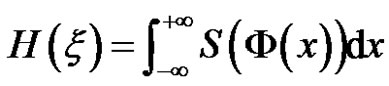 (1)
(1)
where
 .
.
We set  throughout this paper. Figure 1 illustrates Definition 3.1.
throughout this paper. Figure 1 illustrates Definition 3.1.
Through observing Definition 3.1 and Figure 1, we find that the selection of function  is very important. For an uncertain event
is very important. For an uncertain event , if its incredible degree is 0 or 1, then the incident is no uncertainty. Conversely, when this event confidence level is 0.5, the uncertainty of the event is maximums. Therefore, the function
, if its incredible degree is 0 or 1, then the incident is no uncertainty. Conversely, when this event confidence level is 0.5, the uncertainty of the event is maximums. Therefore, the function  must increases on
must increases on  and decreases on
and decreases on . By the enlightenment of Tsallis entropy, we try to define the single parameter entropy of uncertain variable as follows.
. By the enlightenment of Tsallis entropy, we try to define the single parameter entropy of uncertain variable as follows.
Definition 3.2 Suppose that  is an uncertain variable with uncertainty distribution
is an uncertain variable with uncertainty distribution . Then its single parameter entropy is defined by
. Then its single parameter entropy is defined by
 (2)
(2)

Figure 1. The entropy value of uncertain variable if and only if q = 1.
where
 .
.
 is a positive real number. For
is a positive real number. For , it is immediately verified
, it is immediately verified

This means that 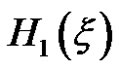 is entropy of uncertain variable. For
is entropy of uncertain variable. For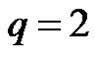 , we have
, we have

It’s clear that  is the quadratic entropy of uncertain variable [20]. Figure 2 illustrates Definition 3.2.
is the quadratic entropy of uncertain variable [20]. Figure 2 illustrates Definition 3.2.
Remark 3.1 From the plot of 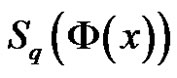 for
for  and typical values of
and typical values of , we notice that
, we notice that 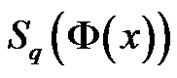 is a monotonic function of
is a monotonic function of . From Definition 3.2 and the Figure 2, we can see the difference between entropy of uncertain variable and single parameter entropy, because the single parameter entropy introduces a adjustable parameter
. From Definition 3.2 and the Figure 2, we can see the difference between entropy of uncertain variable and single parameter entropy, because the single parameter entropy introduces a adjustable parameter , which makes the computing of uncertainty of uncertain variable more general and flexible.
, which makes the computing of uncertainty of uncertain variable more general and flexible.
Example 3.1 Let  be an uncertain variable with uncertain distribution
be an uncertain variable with uncertain distribution

Essentially,  is constant. It follows from the definition of single parameter entropy that
is constant. It follows from the definition of single parameter entropy that

Figure 2. The different entropy value of uncertain variable with parameter q1 = 0.5, q2 = 2, and q3 = 4.

This means that a constant has no uncertainty.
Example 3.2 Suppose  be a linear uncertain variable
be a linear uncertain variable 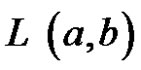 with uncertain distribution
with uncertain distribution

Then its single parameter entropy is

especially, .
.
Example 3.3 Suppose  be a zigzag uncertain variable
be a zigzag uncertain variable  with uncertain distribution
with uncertain distribution

Then its single parameter entropy is

especially, .
.
4. Properties of Single Parameter Entropy
Assuming the uncertain variable with regular distribution, we obtain some theorems of single parameter entropy as follows.
Theorem 4.1 Let 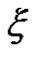 is an uncertain variable. Then the single parameter entropy
is an uncertain variable. Then the single parameter entropy
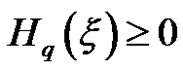 (3)
(3)
where the equality holds if  is a constant.
is a constant.
Proof: From Figure 2, the theorem is clear. As an uncertain variable tends to a constant, the single parameter entropy tends to the minimum 0.
Theorem 4.2 Let  be an uncertain variable, and $c$ a real number. Then
be an uncertain variable, and $c$ a real number. Then
 (4)
(4)
that is, the single parameter entropy is invariant under arbitrary translations.
Proof: Write the uncertainty distribution of  as
as , then
, then

From this equation, we get the uncertainty distribution of uncertain variable as follow:

Using the definition of the single parameter entropy, we find

The theorem is proved.
Theorem 4.3 Let  be an uncertain variable, and let
be an uncertain variable, and let  be a real number, then
be a real number, then
 (5)
(5)
Proof: Denote the uncertain distribution function of  by
by . If
. If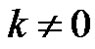 , then the uncertain variable
, then the uncertain variable 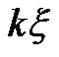 has an uncertain distribution function
has an uncertain distribution function . It follows from the definition of single parameter entropy that
. It follows from the definition of single parameter entropy that

when , we have
, we have .
.
Theorem 4.4 Let  be an uncertain variable with uncertain distribution
be an uncertain variable with uncertain distribution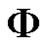 , then
, then
 (6)
(6)
where
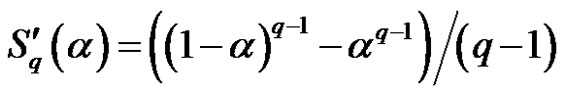 especially,
especially,

Proof: It is obvious that  is a derivable function with
is a derivable function with

Since

and noting that the uncertain variable  has a regular uncertain distribution
has a regular uncertain distribution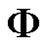 , we have
, we have

By Fubini theorem, we have

The theorem is proved.
Theorem 4.5 Let  and
and  be independent uncertain variables, then for any real numbers
be independent uncertain variables, then for any real numbers  and
and , we have
, we have
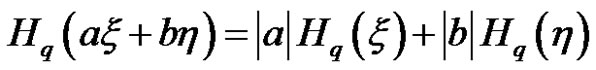 (7)
(7)
Proof: Suppose that  and
and  have uncertainty distribution
have uncertainty distribution  and
and , respectively, and inverse uncertainty distribution
, respectively, and inverse uncertainty distribution  and
and , respectively. Note that the inverse uncertainty distribution of
, respectively. Note that the inverse uncertainty distribution of  is
is

From Theorem 4.4, we have

Since, Theorem 4.3, we obtain

The theorem is proved.
Theorem 4.6 (Alternating Monotone function) Let  be independent uncertain variables with uncertainty distribution
be independent uncertain variables with uncertainty distribution , respectively. If the function $f$ is a strictly increasing with respect to
, respectively. If the function $f$ is a strictly increasing with respect to  and strictly decreasing with respect to
and strictly decreasing with respect to , then
, then  has a single parameter entropy
has a single parameter entropy
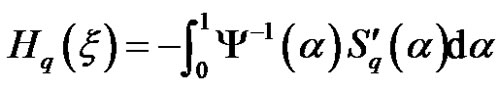 (8)
(8)
where

Proof: Let  be the uncertainty distribution function of
be the uncertainty distribution function of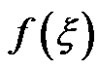 , then it follows from Theorem 2.2 that
, then it follows from Theorem 2.2 that

Since, Theorem 4.4, we have

The theorem is proved.
Example 4.1 Let 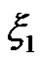 and
and  be independent uncertain variables with regular uncertainty distribution
be independent uncertain variables with regular uncertainty distribution 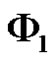 and
and , respectively. Since the function
, respectively. Since the function
 is strictly increasing with respect to
is strictly increasing with respect to  and strictly decreasing with respect to
and strictly decreasing with respect to . From the Theorem 2.2, the inverse uncertainty distribution of the function
. From the Theorem 2.2, the inverse uncertainty distribution of the function  is as follow
is as follow

therefore, its single parameter entropy is

5. Discussions of Single Parameter Entropy
Theorem 5.1 Let  be a uncertain variable with uncertain distribution
be a uncertain variable with uncertain distribution , then
, then
 (9)
(9)
where the equality holds if uncertain distribution .
.
Proof: Let  be a uncertain variable with uncertain distribution
be a uncertain variable with uncertain distribution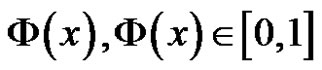 , then
, then

where the equality holds if , that is
, that is . Then
. Then

We complete the proof.
In according to Theorem 5.1, we obtain three situations as follows.
Situation 5.1 If uncertain variable 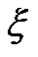 is a constant
is a constant , that is
, that is , then
, then
 (10)
(10)
from Theorem 4.1, we get  since the constant is no uncertainty.
since the constant is no uncertainty.
Situation 5.2 Let uncertain variable , then
, then
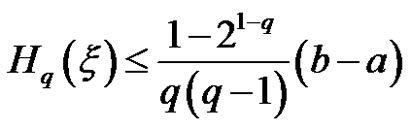 (11)
(11)
According to the fact, we can find the appropriate 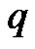 to describe the uncertainty of uncertain variable. Especially, when
to describe the uncertainty of uncertain variable. Especially, when , as
, as
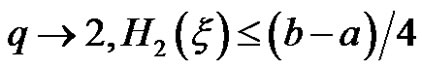 . That is, the single parameter entropy measures the uncertainty of uncertain variable more flexible than the entropy of uncertain variable.
. That is, the single parameter entropy measures the uncertainty of uncertain variable more flexible than the entropy of uncertain variable.
Situation 5.3 Suppose uncertain variable 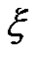 is an impossible event. If we choose
is an impossible event. If we choose , we have
, we have
 (12)
(12)
from Theorem 4.1, we get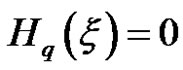 .
.
It is consistent with the reality, which the impossible event can be interpreted that it has no uncertainty.
6. Example of Single Parameter Entropy
Example 6.1 Let uncertain variable , then
, then

By the expert’s experimental data or people’s subjective judgment, we can choose a appropriate 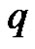 to judge the relation of
to judge the relation of  and
and . Furthermore, we can obtain the relation of
. Furthermore, we can obtain the relation of  and
and . For instance, if two persons’ age
. For instance, if two persons’ age  and they are about 25 years old, Suppose we obtain
and they are about 25 years old, Suppose we obtain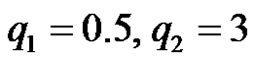 , then
, then ,
, . It is clear that
. It is clear that  is more close to 25 years old than
is more close to 25 years old than .
.
For some case, the entropy of uncertain variable is invalid. However, the single parameter entropy of uncertain variable works well. The follow example shows the point.
Example 6.2 Assume that the uncertain variable  has uncertain distribution as follow
has uncertain distribution as follow

we get the entropy of uncertain variable as follow:

It is clear that entropy of uncertain variable is infinite.
So we consider the single parameter entropy of uncertain variable.

The example illustrate that we can obtain the supremum of uncertainty of uncertain variable by choosing a proper . So the application of single parameter entropy is more extensive.
. So the application of single parameter entropy is more extensive.
7. Conclusion
In this paper, we recalled the entropy of uncertain variable and its properties. On the basis of the entropy of uncertain variable, and inspired by the tsallis entropy, we introduce the single parameter entropy of uncertain variable and explored its several important properties. We have generalized entropy of uncertain variable because of the singe parameter entropy of uncertain variable, which makes the calculating of uncertainty of uncertain variable more general and flexible by choosing an appropriate .
.
NOTES