Stability Criteria of Solutions for Stochastic Set Differential Equations ()
1. Introduction
Recently, the field of stochastic differential equations (SDEs) has been studying in a very abstract method. Instead of considering the behaviours of one solution of (SDEs), one studies its set-valued solution. Instead of studying a (SDEs), some study stochastic differential inclusion (SDIs) (see e.g. [2-4] and references therein), stochastic fuzzy differential equations (SFDEs), (see e.g. [5-6] and references therein) stochastic set differential equations (SSDEs) (see e.g. [7-10] and references therein), stochastic set differential equations with selector (see [11-13]). Latest, the existence and uniqueness of solutions to the stochastic set differential equations were studied in [1]. We remark that the problems of properties of stochastic set solution are still open.
We organize this paper as follows: In Section 2, we recall some basic concepts and notations which are useful in next sections. In Section 3, we study some kinds of stability properties such as stable, asymptotically stable, exponentially stable by Lyapunov and some other stability criterion. In Section 4, we give the examples and further research of this paper.
2. Preliminaries
We recall some notations and concepts presented in detail in recent series works of V. Lakshmikantham et al (see [14]). Let  denote the collection of all nonempty compact convex subsets of
denote the collection of all nonempty compact convex subsets of . Given
. Given , the Hausdorff distance between A and B is defined by
, the Hausdorff distance between A and B is defined by
 (2.1)
(2.1)
and —the zero points set in
—the zero points set in . It is known that
. It is known that 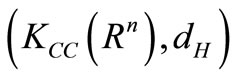 is a complete metric space and
is a complete metric space and
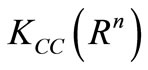 is a complete and separable with respect to
is a complete and separable with respect to . We define the magnitude of a nonempty subset
. We define the magnitude of a nonempty subset  as,
as,


The Hausdorff metric (2.1) satisfes the properties below:
1) 

2) 
3) 
4) 
for all  and
and .
.
If  and
and , then
, then
 Given a complete probability space
Given a complete probability space 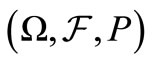 with a filtration
with a filtration
 satisfying the usual conditions. Let
satisfying the usual conditions. Let
 be an
be an —adapted one dimensional Wiener process defined on
—adapted one dimensional Wiener process defined on 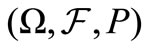 and
and , with
, with  is one-dimensional “white noise”, i.e., the time derivative of the Wiener process. In [1], authors considered the initial valued problem (IVP) for a set stochastic differential equation (SSDE) as follows
is one-dimensional “white noise”, i.e., the time derivative of the Wiener process. In [1], authors considered the initial valued problem (IVP) for a set stochastic differential equation (SSDE) as follows
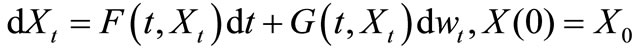 (2.2)
(2.2)
where ,
,
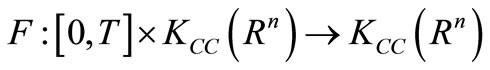
 is measurable multifunction and Aumann integrably bounded.
is measurable multifunction and Aumann integrably bounded.

 is measurable multifunction and
is measurable multifunction and  integrably bounded,
integrably bounded,  is an
is an  -measurable multifunction.
-measurable multifunction.
Definition 2.1. (see [1]) Let a set-valued stochastic process  satisfy:
satisfy:
1)  for every
for every  ;
;
2) 
is continuous mapping with respect to the metric ;
;
3) for every :
:

where  is an
is an —measurable multifunction. Then
—measurable multifunction. Then  is solution of (2.2).
is solution of (2.2).
Definition 2.2. Let set-valued stochastic processes , we have the following definitions:
, we have the following definitions:
1) For every ,
,

2) For every ,
,

Using the properties of the Hausdorff distance one can formulate the following results
Lemma 2.1.
1) if
then 
2) if

then 
3) If  and
and  reconstants, then
reconstants, then 
Corollary 2.1. (see [7]) Let set-valued stochastic processes  we have the following confirms:
we have the following confirms:
1) ;
;
2)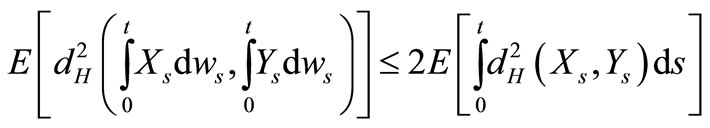 ;
;
3) ;
;
4) .
.
Definition 2.3. A solution 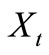 to Equation (2.2) is unique if for every
to Equation (2.2) is unique if for every :
:

where  is any solution to Equation (2.2).
is any solution to Equation (2.2).
Assume that  satisfy the following hypotheses:
satisfy the following hypotheses:
(H1) For every set  the mappings
the mappings
 :
:  are nonanticipating multifunctions.
are nonanticipating multifunctions.
(H2) There exists a constant , such that
, such that

(H3) There exists a constant , such that
, such that

(H4) There exists a function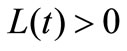 , such that
, such that

where .
.
(H5) There exists a function , such that
, such that

where .
.
Corollary 2.2. (see [1], Theorem 7) Assume  be an
be an —measurable multifunction and F, G satisfy (H1)-(H3), then SSDE (2.2) has a unique solution and satisfies estimate
—measurable multifunction and F, G satisfy (H1)-(H3), then SSDE (2.2) has a unique solution and satisfies estimate

Corollary 2.3. Assume  be an
be an —measurable multifunction and F, G satisfy (H1), (H4)-(H5), then SSDE (2.2) has a unique solution and satisfies estimate
—measurable multifunction and F, G satisfy (H1), (H4)-(H5), then SSDE (2.2) has a unique solution and satisfies estimate

3. Main Results
In this section, we study some kinds of stability properties such as stable, asymptotically stable, exponentially stable by Lyapunov and some other stability criteria such as equi, uniform and equi-asymptotical stabilities for SSDE.
Definition 3.1. The trivial stochastic set solution of SSDE Equation (2.2) is said to be
(LS) Lyapunov stable, if for each  and
and 
there exist a , such that
, such that 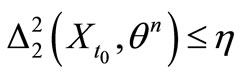
implies .
.
(ALS) Asymptotical Lyapunov stable, if it is (LS) and
 .
.
(ELS) Exponent Lyapunov stable, if there exist  , such that:
, such that:

Definition 3.2. The trivial stochastic set solution of SSDE Equation (2.2) is said to be:
(S1) Equi-stable, if for each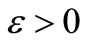 , and
, and  there exists
there exists  such that
such that  implies that
implies that ,
, ;
;
(S2) Uniformly stable, if  in (S1) is independent of
in (S1) is independent of ;
;
(S3) Quasi-equi-asymptotically stable, if for each , there exists
, there exists  and
and 
such that  implies
implies , for all
, for all ;
;
(S4) Quasi-uniformly-asymptotically stable, if  and
and  in (S3) are independent of
in (S3) are independent of ;
;
(S5) Equi-asymptotically stable, if (S1) and (S3) hold simultaneously;
(S6) Uniformly asymptotically stable, if (S2) and (S4) hold simultaneously;
(S7) Exponent-asymptotically stable, if exist  such that
such that  for all
for all 
Lemma 3.1. According to the Definitions 3.1 and Definition 3.2, we can say that 1) The stochastic set solution of SSDE E (2.2) is (S1) if and only if it is (LS) that means (S1)  (LS).
(LS).
2) (S6)  (ALS).
(ALS).
3) (S7)  (ELS).
(ELS).
4) (S6) or (ALS)  (S6).
(S6).
5) (S6)  (S4).
(S4).
Thus we have to prove (S1), (S6) and (S7).
Next, we present some results about (S1)-(S6) of solution with using the Lyapunov-like functions.
Theorem 3.1. Suppose that the positive Lyapunov-like function satisfies the following conditions:
satisfies the following conditions:
1) where
where  is Lipschitz constant, for all
is Lipschitz constant, for all ,
,
 ,
, ;
;
2) The Dini derivative

where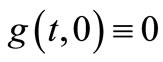 ,
, ;
;
If  is any solution of SSDE Equation
is any solution of SSDE Equation
(2.2) Such that , then we have
, then we have

where 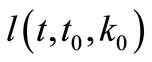 is a maximal solution of ordinary differential equation (ODE)
is a maximal solution of ordinary differential equation (ODE)
 (3.1)
(3.1)
Proof. Let  be any solution of SSDE Equation (2.2) existing on
be any solution of SSDE Equation (2.2) existing on . We define the function
. We define the function  so that
so that .
.
Now for small , by our assumption it follows that
, by our assumption it follows that

by using the Lipschitz condition give (1). Thus

Since

and  is any solution of SSDE Equation (2.1), we find that
is any solution of SSDE Equation (2.1), we find that

We therefore have the scalar differential inequality 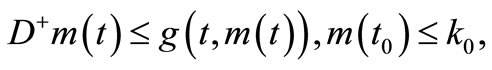 which yields, as before, the estimate
which yields, as before, the estimate  where
where  is a maximal solution of ODE (3.1). This proof is complete.
is a maximal solution of ODE (3.1). This proof is complete.
Corollary 3.1. If the Lyapunov-like function 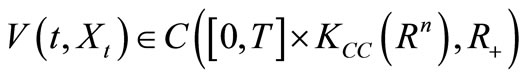 satisfies conditions in Theorem 3.1 then we have the estimate:
satisfies conditions in Theorem 3.1 then we have the estimate:

Next, putting

Theorem 3.2. Assume that for SSDE Equation (2.2) exists the Lyapunov like function  which satisfies the conditions of Theorem 3.1.
which satisfies the conditions of Theorem 3.1.
a) If there exist the positive functions  are strictly increasing such that:
are strictly increasing such that:
1) 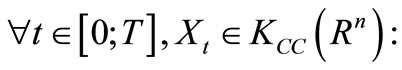

and , then (S1) holds.
, then (S1) holds.
Futhermore, there exists  such that
such that
2) If , then (S3) holds.
, then (S3) holds.
3) If , then (S5) holds.
, then (S5) holds.
b) If there exist the positive functions 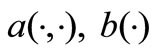 are strictly increasing and
are strictly increasing and 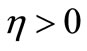 such that:
such that:
1) 
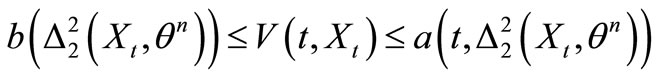
and , then (S2) holds.
, then (S2) holds.
Futhermore, there exists  such that.
such that.
2) If , then (S4) holds.
, then (S4) holds.
3) If  then (S6) holds.
then (S6) holds.
Proof. Let  and
and  be given, choosing
be given, choosing 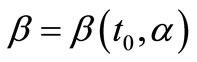 such that
such that  with this we have (S1).
with this we have (S1).
If this is not true, there would exists a stochastic set solution  of SSDE Equation (2.2) and
of SSDE Equation (2.2) and  such that
such that

with . By using Corollary 3.1 and a/1, we have
. By using Corollary 3.1 and a/1, we have
 and condition
and condition
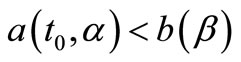 as result, yield:
as result, yield:

This contradiction proves that (S1) holds.
Next, we have to prove that:  there exists a
there exists a  and number
and number  such that:
such that:
 implies
implies for
for
 . Let
. Let  and
and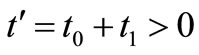 .
.
Choosing  such that
such that  with this we have (S3). If this is not true, there would exists a stochastic set solution
with this we have (S3). If this is not true, there would exists a stochastic set solution  of SSDE Equation
of SSDE Equation
(2.2) such that,  and
and where
where , for
, for 
By using assumption (a/2) of this theorem shows that ,
, 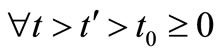 and yields:
and yields:

This contradiction proves that (S3) holds.
The affirmation for (S5) is proved analogous to the proof of the affirmations for (S1), (S3).
Next, we have to prove that (S2) holds:
By 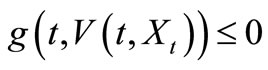 implies
implies 
and ,
, .
.

Thus for all  and
and 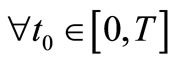 the affirmation for (S1) holds, that means the affirmation for (S2) holds.
the affirmation for (S1) holds, that means the affirmation for (S2) holds.
Next, we have to prove that (S4) holds. According to assumption b) of Theorem 3.2
1) 
2) 
For all , we have
, we have

As a result,
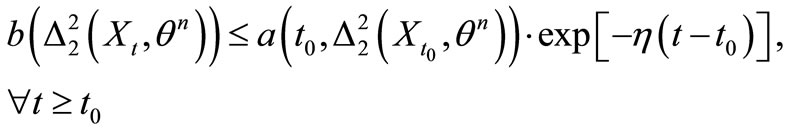
and (S4) holds.
The affirmation for (S6) is proved analogous to the proof of the affirmations for (S2), (S4).
Corollary 3.2. Assume that for SSDE Equation (2.2) exists the Lyapunov like function  which satisfies the conditions of Theorem 3.1, and exist the positive numbers
which satisfies the conditions of Theorem 3.1, and exist the positive numbers  such that
such that 
 .
.
If , then (S7) holds.
, then (S7) holds.
Proof. The proof for (S7) is proved analogous to the proof of the affirmations for (S4).
4. Some Applications of Stochastic Set Differential Equations
For example, in a finance market we consider some stock price at time 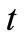 denoted by
denoted by  which is a random variable defined on the probability space
which is a random variable defined on the probability space . Owing to the quick fluctuation of the stock price from time to time or to the existence of missing data, we may not precisely know the price
. Owing to the quick fluctuation of the stock price from time to time or to the existence of missing data, we may not precisely know the price . A possible model for this situation would be to give the upper and the lower prices (i.e. a margin for the error in the observation). Then we obtain an nterval
. A possible model for this situation would be to give the upper and the lower prices (i.e. a margin for the error in the observation). Then we obtain an nterval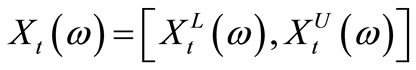 , which is a special kind of a set-valued random variable, ontains not only randomness but also impreciseness, and we assume
, which is a special kind of a set-valued random variable, ontains not only randomness but also impreciseness, and we assume  is certainly in this interval.
is certainly in this interval.
For example different, in environmental of the insurance premium, the risks is considered a main material of this industry. Beside that, the risks are random factors and associating with premiums, so insurance premiums should be built on the basis of risks to price insurance which could compensate and balance the damage occurs to their business costs. Otherwise, the risks are some kinds different and levels of influence are different, so they could influence to levels of price of the insurance premium.
Hence, we may not precisely know the price of the insurance premium such that be beneficial to company of the insurance and customers. Then, in special the case we assume  is certainly in this interval which admissible prices.
is certainly in this interval which admissible prices.
Example 4.1. (Stock prices) Let  denote the price of a stock at time
denote the price of a stock at time , where
, where  (i.e. interval-valued). We can model the evolution of
(i.e. interval-valued). We can model the evolution of  and the relative change of price, evolves according to the SSDE under the form
and the relative change of price, evolves according to the SSDE under the form
 (4.1)
(4.1)
for all , for certain constants
, for certain constants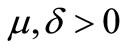 , called the drift and the volatility of the stock.
, called the drift and the volatility of the stock.
Since coefficients in Equation (4.1) satisfy the conditions in Corollary 2.2, there is a unique solution of Equation (4.1). This means that for  SSDE (4.1) satisfies the following interval-valued stochastic differential equation
SSDE (4.1) satisfies the following interval-valued stochastic differential equation
 (4.2)
(4.2)
for all . That is,
. That is,

Since ,
,  and
and  are the solutions of the following stochastic differential system
are the solutions of the following stochastic differential system
 (4.3)
(4.3)
 (4.4)
(4.4)
We can slove Equation (4.3) and Equation (4.4) by classic methods. Thus, the solutions of Equation (4.3) and Equation (4.4) respecttively are

and
 .
.
Its graphical representation can be seen in Figure 1.
From here it is easily verifiable stability criteria of solution to Equation (4.1).
5. Further Research
In the future, we will concentrate all our efforts on other properties of this kind of equation discussed in our paper, such as on the existence of extremal solutions for SSDEs (2.2). Beside that, set-valued stochastic differential equations and their solutions seem to be a starting point for

Figure 1. Solution of Example 4.1 in case μ = 2, δ = 1.
further development in the theory of control for SSDEs. Below we present the main idea, we consider the setvalued stochastic control differential equations (SSCDEs) under the form
 (4.5)
(4.5)

where 
are continuous multifunctions, state set  and
and  is different controls, inclusion: admissible control, feedback control and contraction control. The problems of the existence and properties of solutions to SSCDEs Equation (4.5) is still open.
is different controls, inclusion: admissible control, feedback control and contraction control. The problems of the existence and properties of solutions to SSCDEs Equation (4.5) is still open.
6. Acknowledgements
The authors gratefully acknowledge the referees for their careful reading and many valuable remarks which improved the presentation of the paper. The authors thank the partial financial support of AM editorial office.