A Representation of the Maximal Set in Choice Problems Where Information Is Incomplete ()
1. Introduction
The economic approach to rational behaviour assumes that each individual makes choices by selecting, from each feasible set of alternatives, those which maximize his own preference relation. The classical framework of optimization used in standard choice theory recommends choosing, among the feasible options, a best alternative. According to this modeling of a choice process, the optimal choice set consists of the best alternatives according to a binary relation R. So, if A is the feasible set of alternatives and R is a binary relation over A, a formalization of this idea requires the following definition of the optimal choice set
:
.
Many economists have pointed out that this stringent form of maximization might not be the kind of optimization that one can apply in problems where information is incomplete. For example, the Nobel-Prize winner Amartya Sen ( [5] , Page 763) has pointed out that: “The general discipline of maximization differs from the special case of optimization in taking an alternative as choosable when it is not known to be worse than any other. [...] The basic contrast between maximization and optimization arises from the possibility that the preference ranking R may be incomplete.” That is, where R (over A) is considered to be incomplete, optimization recommends focusing on the set of alternatives
which are maximal with respect to R. To define a maximal set we use the asymmetric part
of R. So, the optimal choice set is defined as:
.
In general (for any binary relation R and any non-empty feasible set A) we have that
, where the equality holds in case that R is complete. If a binary relation R is transitive, Banerjee and Pattanaik ( [1] , Proposition 3.2) showed that the maximal set generated by R is the union of the optimal choice sets generated by all possible orderings extending R. That is,
,
where
is the set of ordering extensions of R. In other words, Banerjee and Pattanaik’s result starts from a transitive binary relation R in that there are some ordered pairs, say
, over which R does not convey any information, and answers whether all the information originally conveyed by R can be recovered in terms of the set of all ordering extensions of R. Suzumura and Xu [2] extended Banerjee and Pattanaik’s result by relaxing the axiom of transitivity to the axiom that Suzumura calls consistency [6] . Arló Costa in ( [3] , Page 19) pointed out that: “When R is complete
. Moreover, a maximal set
can always be replicated by optimizing a complete relation
obtained from R by transforming incomparabilities into indifferences. Obviously this new relation
has to be complete but it might fail to be transitive.” For example, let
over the feasible set
. Then,
is an extension of R satisfying
. Obviously,
is complete but not transitive. This example shows that the extended binary relations used in order to replicate maximizing process tend not to be transitive. So, we must expect that an optimizing model cannot require the transitivity of the binary relation used in the optimizing model.
In this paper, I extend the Banerjee-Pattanaik’s and Suzumura-Xu’s results to arbitrary binary relations whose extensions are complete and not necessarily transitive.
2. Basic Notations and Definitions
We recall some definitions from Suzumura [7] , Cato [8] and Duggan [9] .
Let X be a non-empty universal set of alternatives and
be a binary relation on X. Let
be the set of all subsets of X. We sometimes abbreviate
as
. The asymmetric part of R is defined by
and the symmetric part of R is defined by
.
Thef non-comparable part
of R is defined by letting, for all
,
if and only if
and
. For any subset A of X, an element
is a maximal element in A with respect to R if for all
,
. Dually is defined the notion of minimal element. The set of all maximal elements in A with respect to R is the maximal set of A, to be denoted by
. Likewise, an element
is a best element in A with respect to R if
holds for all
. The set of all best elements in A with respect to R is the greatest set of A, to be denoted by
. We say that R on X is 1) reflexive if for each
; 2) asymmetric if for each
implies
; 3) transitive if for all
, [
and
]
; 4) anti-symmetric if for each
, [
and
]
; 5) total if for each
,
we have
or
; 6) complete if for each
, we have
or
. It follows that R is complete if and only if it is reflexive and total. The following combination of properties are considered in the next theorems. A binary relation R on X is 1) a quasi-ordering if R is reflexive and transitive; 2) an ordering if R is a total quasi-ordering; 4) a partial order if R is an anti-symmetric quasi-ordering; 5) a linear ordering if R is an anti-symmetric ordering; 6) tournament if R is asymmetric and total. For any binary relation R, let
be the transitive closure of R, which is defined by
if and only if there exist
and
such that
for all
and
. The relation R is consistent, if for all
,
implies
(see [6] ).
A binary relation
is an extension of a binary relation R if and only if
and
. If an extension
of R is an ordering, we call it an ordering extension of R. We call a binary relation
on X satisfying
,
and
a strict extension of R. For a given binary relation R on X, let
be the set of all ordering extensions of R and
be the set of all strict ordering extensions of R.
A set X is well-ordered if there is a binary relation
on X which is a linear order and for which every non-empty subset of X has a minimal element. A chain
is a class such that
implies
or
. A partially ordered set is a set X together with a partial ordering
. Zorn’s lemma states that if X is a partially ordered set such that every chain in X has an upper bound, then X has a maximal element.
3. Generalization of Banerjee-Pattanaik’s Result
Arrow ( [10] , page 64), Hansson [11] and Fishburn [12] prove that any quasi-ordering has an ordering extension. Banerjee and Pattanaik in ( [1] , Page 195) give an example of a quasi-ordering R defined on a set X such that
for some
. In this case,
will be empty for every ordering extension
of R in X. According to the Authors’ interpretation, this difficulty has an origin very different from the issue on non-comparability on which they have focused in their paper. Asuming that non-comparability is valid jointly to the above result of Arrow, Hansson and Fishburn, we come to the conclusion that the form
is equivalent to the non-emptiness of
. Suzumura and Xu [2] call the choice rule of Banerjee and Pattanaik, choice functional recoverability, that is:
Definition 3.1. ( [2] , Definition 3.1). Let R be a binary relation on X. We say that R is choice-functionally recoverable if and only if
holds for all non-empty subsets
.
According to what we have said above, the choice-functional recoverability of a quasi-ordering is equivalent to the non-emptiness of the set of its strict ordering extensions. The following theorem, which is due to Banerjee and Pattanaik [1] , is the first important result in the theory of choice-functional recoverability (see [2] ).
Theorem 1. A quasi-ordering R is choice-functionally recoverable if and only if
.
While the choice-functional recoverability of a quasi-ordering R is equivalent to the non-emptiness of the set of its strict ordering extensions, Suzumura and Xu [7] show by counter-example that the same is not necessarily true for a reflexive and consistent binary relation.
In order to generalize Theorem 1, Suzumura and Xu consider the following assumption (
):
(
) Let R be a binary relation on X. For all
,
implies
.
With Assumption (
), Suzumura and Xu generalize the result of Banerjee and Pattanaik as follows:
Theorem 2. A reflexive and consistent binary relation R on X is choice-functionally recoverable if and only if
and Assumption (
) hold.
Now, I give a more general theorem of recoverability of choice functions for binary relations whose extensions are total and not necessarily reflexive and transitive.
The following definition is of use in the next results.
Definition 3.2. (see [4] , Definitions 8 and 10). Let
be a class of binary relations on X. We say that
is: (
) Closed upward, if for all chains
in
we have that
. (
) Arc-receptive if for every distinct
and all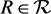 ,
, 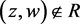 implies that there exists an extension
implies that there exists an extension  of
of 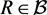 such that
such that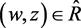 .
.
Lemma. Let R be a binary relation on X and let  be a closed upward and arc-receptive collection of binary relations on X such that
be a closed upward and arc-receptive collection of binary relations on X such that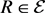 . Suppose that
. Suppose that  and A is an arbitrary subset of X. Then, there exists a binary relation
and A is an arbitrary subset of X. Then, there exists a binary relation 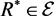 such that for each
such that for each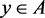 , if
, if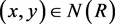 , then
, then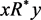 .
.
Proof. Fix an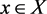 . Given
. Given , let
, let . The Well-Ordering Principle asserts that every set X can be well-ordered; that is, if K is any set, then there exists a well-ordered set
. The Well-Ordering Principle asserts that every set X can be well-ordered; that is, if K is any set, then there exists a well-ordered set 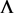 which serves as an index set for the elements of K, so we may write
which serves as an index set for the elements of K, so we may write

By definition, K has a first element, a second element, a third element and so on. Let . Then,
. Then, ![]() implies that
implies that![]() . Since R is arc-receptive, there exists an extension
. Since R is arc-receptive, there exists an extension ![]() of R such that
of R such that ![]() and
and![]() . For each
. For each![]() , we define
, we define![]() . Since
. Since ![]() is closed upward, we conclude that
is closed upward, we conclude that![]() . Let now
. Let now
![]()
Let ![]() be a chain in
be a chain in ![]() and let
and let![]() . Then,
. Then,
![]()
with![]() . Since
. Since ![]() is closed upward, we conclude that
is closed upward, we conclude that![]() . But then,
. But then, ![]() implies that
implies that![]() . Therefore, any chain in
. Therefore, any chain in ![]() has an upper bound in
has an upper bound in ![]() (with respect to set inclusion). By Zorn’s lemma, there is a maximal element
(with respect to set inclusion). By Zorn’s lemma, there is a maximal element ![]() in
in![]() . Then,
. Then, ![]() for some
for some![]() . If
. If![]() , then there exists
, then there exists ![]() such that
such that![]() . It follows that
. It follows that
![]() ,
,
a contradiction to maximality of![]() . It follows that
. It follows that![]() . Therefore, for each
. Therefore, for each ![]() with
with![]() , we have
, we have ![]() for some
for some![]() . Hence, we have
. Hence, we have ![]() holds.
holds.
For a given binary relation R on X, let ![]() be the set of all strict total extensions of R.
be the set of all strict total extensions of R.
Theorem 3. Let R be a binary relation on X and let ![]() be a be a closed upward and arc-receptive collection of binary relations on X such that
be a be a closed upward and arc-receptive collection of binary relations on X such that![]() . Then, R is choice-functionally recoverable if and only if
. Then, R is choice-functionally recoverable if and only if![]() .
.
Proof. Let R, ![]() and
and ![]() be as in the supposition and let A be a subset of X. We need to show that
be as in the supposition and let A be a subset of X. We need to show that
![]() .
.
We first show the ![]() inclusion. Take any
inclusion. Take any![]() . Then,
. Then, ![]() for all
for all![]() . Since
. Since ![]() we have that
we have that ![]() for all
for all![]() . Therefore,
. Therefore,![]() . It follows that
. It follows that![]() . Since
. Since ![]() is total,
is total, ![]() , and thus,
, and thus,![]() . Therefore,
. Therefore,
![]() .
.
It suffices to show the ![]() inclusion. Take
inclusion. Take![]() . Then, for each
. Then, for each![]() ,
, ![]() holds. On the other hand,
holds. On the other hand,
![]() .
.
By Lemma 3, there exists a binary relation ![]() in
in ![]() such that for each
such that for each ![]() and
and![]() , we have
, we have![]() . If
. If ![]() and
and![]() , then
, then ![]() implies that
implies that ![]() or
or![]() . Therefore, for each
. Therefore, for each ![]() we have
we have![]() . If
. If ![]() is total, then
is total, then
![]() .
.
Consider now the case where ![]() is non-total. Let
is non-total. Let
![]() and
and![]() .
.
We have that![]() , so this class is non-empty. Let
, so this class is non-empty. Let ![]() be a chain in
be a chain in![]() , and let
, and let![]() . Then,
. Then,![]() . To prove that
. To prove that![]() , take any
, take any ![]() and suppose to the contrary that
and suppose to the contrary that![]() . Clearly,
. Clearly, ![]() and for each
and for each![]() ,
,![]() . Since
. Since
![]()
we conclude that![]() . Hence,
. Hence, ![]() for some
for some![]() , a contradiction to
, a contradiction to![]() .
.
It follows that![]() . Since
. Since ![]() is closed upward, we conclude that
is closed upward, we conclude that ![]() which implies that
which implies that![]() . Therefore, any chain in
. Therefore, any chain in ![]() has an upper bound in
has an upper bound in ![]() (with respect to set inclusion). By Zorn’s lemma, there is a maximal element
(with respect to set inclusion). By Zorn’s lemma, there is a maximal element ![]() in
in![]() . If there existed distinct
. If there existed distinct ![]() not comparable with respect to
not comparable with respect to![]() , then the fact that
, then the fact that ![]() is arc-receptive would imply the existence of an extension
is arc-receptive would imply the existence of an extension ![]() of
of ![]() with
with![]() . But then,
. But then, ![]() , which contradicts the maximality of
, which contradicts the maximality of ![]() in
in![]() . The last contradiction shows that
. The last contradiction shows that ![]() is total. Therefore, for each
is total. Therefore, for each![]() , we have
, we have![]() . It follows that
. It follows that
![]() .
.
Therefore, R is choice-functionally recoverable.
To prove the converse, suppose that R is choice-functionally recoverable, so that we have
![]()
for all non-empty subsets A of X. Clearly,![]() .
.
Theorem 1 of Banerjee and Pattanaik as well as Theorem 2 of Suzumura and Xu are corollaries of Theorem 3.
Proof of Theorem 1. Let R be a quasi-ordering on X and let ![]() be the collection of all quasi-orderings on X which are extensions of R. By Arrow [10] , Hansson [11] and Fishburn [12] this set is non-empty. Then, by [4, Propositions 5 and 7] we have that
be the collection of all quasi-orderings on X which are extensions of R. By Arrow [10] , Hansson [11] and Fishburn [12] this set is non-empty. Then, by [4, Propositions 5 and 7] we have that ![]() is closed upward and arc-receptive and thus Theorem 3 implies directly Theorem 1.
is closed upward and arc-receptive and thus Theorem 3 implies directly Theorem 1.
Proof of Theorem 2. Let R be a reflexive and consistent binary relation on X satisfying assumption (![]() ) and let
) and let ![]() be the collection of all reflexive and consistent extensions of R satisfying assumption (
be the collection of all reflexive and consistent extensions of R satisfying assumption (![]() ). Let
). Let ![]() be a chain in
be a chain in![]() . Then, [4, Propositions 5 and 7] implies that
. Then, [4, Propositions 5 and 7] implies that ![]() is reflexive and consistent. We now show that
is reflexive and consistent. We now show that ![]() satisfies assumption (
satisfies assumption (![]() ). Let
). Let
![]() .
.
Then, there exists ![]() such that
such that![]() . It follows that
. It follows that
![]() .
.
Therefore, ![]() is closed upward. Moreover, for all distinct x and y and for all reflexive and consistent binary relations Q,
is closed upward. Moreover, for all distinct x and y and for all reflexive and consistent binary relations Q, ![]() implies
implies
![]() .
.
Clearly, ![]() is a reflexive and consistent extension of Q which satisfies assumption (
is a reflexive and consistent extension of Q which satisfies assumption (![]() ). Therefore,
). Therefore, ![]() is arc-receptive. On the other hand, if R is choice-functionally recoverable, then Assumption (
is arc-receptive. On the other hand, if R is choice-functionally recoverable, then Assumption (![]() ) holds (see ( [2] , Page 26)). Since reflexivity, totalness and consistency imply transitivity, Theorem 3 implies Theorem 1.
) holds (see ( [2] , Page 26)). Since reflexivity, totalness and consistency imply transitivity, Theorem 3 implies Theorem 1.
4. Conclusion
For much of the economic analysis, the characterization of maximizing the utility of individuals as a criterion of rationality (optimization) can pose serious problems, especially in the case where no alternative can be identified as the best choice. This kind of optimization is often ineffective for finding a choice set, which only requires choosing an alternative that is not judged to be worse than any other. A nice regularity condition to the above procedure for the construction of non-empty choice sets is acyclicity. This is because acyclicity is sufficient for the existence of maximal elements when the set of alternatives is finite, and it is also necessary for the existence of maximal elements in all subsets of alternatives. In the special case in which R is transitive, Banerjee and Pattanaik [1] show that the maximal set generated by a quasi-ordering R is the union of the optimal sets generated by all possible ordering extensions of R. This result was extended by Suzumura and Xu [2] by relaxing the axiom of transitivity to the axiom of consistency [6] . The choice rule, which relates the maximal set generated by a binary relation R and the union of the sets of best elements generated by all possible orderings extending R, is called by the name of “the choice functional recoverability” (see [2] , Definition 3.1). In the case of choice-functional recoverability achieved by the above mentioned authors, we focus on the recoverability of the choice set defined in terms of R by means of the set of the best elements defined in terms of each and every transitive and complete extension of R. However, as Arló Costa pointed out in [3] by giving some examples, an optimizing model of a binary relation cannot require the transitivity of the extended binary relation used in the optimizing model. In this paper, the choice rule defined by Theorem 3 satisfies the requirements posed by Arló Costa in [3] . On the other hand, this choice rule ensures the recoverability of the choice set defined in terms of a non-necessarily transitive binary relation R, by means of the set of the best elements defined in terms of each and every total extension of R. For example, if in Theorem 3, R is an asymmetric binary relation, then the result is still valid with ![]() being the set of all tournament extensions of R in X.
being the set of all tournament extensions of R in X.
Conflicts of Interest
The authors declare no conflicts of interest regarding the publication of this paper.