

1. Introduction
In recent years, many scholars were enthusiastic for the stability and the bifurcation of truncated model of the Navier-Stokes equations [1]-[5]. A pioneering work by Lorenz [6] of 1963, concerning the Saltzman equations for convection between plates, represents the first attempt to study the partial differential equations that govern a fluid flow through truncation of a suitable Fourier expansion to a finite number of components (“modes”). Later in the twentieth century, Valter Franceschini made a further expansion in this research field and worked with other scholars to study the Navier-Stokes equations. They consider the following plane incompressible Navier-Stokes equations on the torus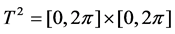 , the velocity field
, the velocity field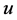 , the pressure
, the pressure  and (periodic) volume force.
and (periodic) volume force. 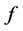 is expanded in Fourier series on a torus. Some model Lorenz-like equations have been proposed, then they have studied three-dimensional Navier-Stokes, the equation in
is expanded in Fourier series on a torus. Some model Lorenz-like equations have been proposed, then they have studied three-dimensional Navier-Stokes, the equation in 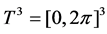 and obtained somenonlinear system, and discussed these complex system in detail in [3]-[5].
and obtained somenonlinear system, and discussed these complex system in detail in [3]-[5].
In this paper, we expand the plane incompressible Navier-Stokes equations in Fourier series on a torus and obtain a new five-mode equation. Dynamical behaviors of this new chaotic system, including some basic dynamical properties, bifurcations, and routes to chaos, etc., have been investigated both theoretically and numerically by changing Reynolds number. Our purpose is to study how the phenomena of the model changes when the modes in the truncation are changed. The existence of attractor and the global stability of the equations have been firmly verified and these theories can be used in other similar model. Furthermore, some dynamical behavior features of the new chaos system in a certain range of the Reynolds number, such as bifurcation diagram, Lyapunov exponent spectrum, Poincare section, power spectrum and return map, are presented.
We expanded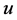 ,
, 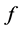 ,
, 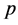 in Frourier series, and take
in Frourier series, and take 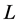 as the set of vectors
as the set of vectors 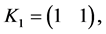
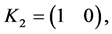
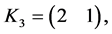
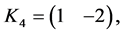
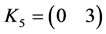 and their opposites. With a lot of calculation, we obtain the following five-mode Lorenz-like system
and their opposites. With a lot of calculation, we obtain the following five-mode Lorenz-like system
 (1)
(1)
Accordingly, we get the new five-mode nonlinear equation, which is similar to the Lorenz equation. We call it a Lorenz-like equation. By changing both the signs of 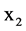 and
and![]() , the property of the equations is unchanged. This indicates that system (1) has following symmetry property
, the property of the equations is unchanged. This indicates that system (1) has following symmetry property
![]() .
.
2. The Stationary Solution and Their Stability Properties
In the following we linearize the nonlinear Equation (1) and discuss the stability of its stationary solutions.
a) For![]() , there is only one stationary solution
, there is only one stationary solution![]() . Substituting
. Substituting
the stationary solution ![]() into the Jacobian matrix we obtain the characteristic equation of Jacobian matrix
into the Jacobian matrix we obtain the characteristic equation of Jacobian matrix
![]()
For![]() , since all eigenvalues of the Jacobian matrix are negative, the stationary solution
, since all eigenvalues of the Jacobian matrix are negative, the stationary solution ![]() is stable (this is a particular case of general results on the theory of the Navier-Stokes equations [7]), and numerical evidence suggests that the
is stable (this is a particular case of general results on the theory of the Navier-Stokes equations [7]), and numerical evidence suggests that the ![]() is a global attract or for all
is a global attract or for all![]() .
.
b) For![]() , there are 3 stationary solutions: the old one
, there are 3 stationary solutions: the old one![]() , which has become unstable
, which has become unstable
as a consequence of the crossing of the imaginary axis by one of the eigenvalues of the Jacobian matrix) and two additional ![]() as follow
as follow
![]() .
.
By a similar discussion we get the characteristic equation of Jacobian matrix at ![]() is:
is:
![]() (2)
(2)
owing to roots of the characteristic Equation (2) have a negative real part, stationary solution ![]() are stable. Numerical evidences indicate that any randomly chosen initial data is attracted by them, so they are global attractors. When
are stable. Numerical evidences indicate that any randomly chosen initial data is attracted by them, so they are global attractors. When
c) For![]() , there are 7 stationary solutions: the old ones
, there are 7 stationary solutions: the old ones![]() ,
, ![]() , and
, and![]() , with components
, with components
![]() .
.
The first three are now always unstable, while the new four are stable for ![]() and numerically they attract any randomly chosen initial data. At
and numerically they attract any randomly chosen initial data. At ![]() the fours table stationary solutions become unstable because a pair of complex conjugate eigenvalues crosses the imaginary axis, and four stable periodic orbits around the fixed points
the fours table stationary solutions become unstable because a pair of complex conjugate eigenvalues crosses the imaginary axis, and four stable periodic orbits around the fixed points ![]() arise via a Hopf bifurcation, we will give a detailed discussion in the Section 4.
arise via a Hopf bifurcation, we will give a detailed discussion in the Section 4.
3. The Existence of Attractor and Analysis of Global Stability
In the following, we discuss the existence of attractor of the system (1), assume that
![]() , by calculating we get
, by calculating we get![]() . Using the Gronwall inequality [8], we get
. Using the Gronwall inequality [8], we get![]() . Therefore, we have
. Therefore, we have![]() . If
. If ![]() big enough,
big enough,
sphere ![]() is an not only functional invariant set but also absorbing set. As a result the system (1) has the global attractor [8] [9].
is an not only functional invariant set but also absorbing set. As a result the system (1) has the global attractor [8] [9].
We construct a following Liapunov function of the system (1):
![]() (3)
(3)
Setting![]() , obviously, when k is a positive constant, it represents a sphere, which is labeled as E. By calculating we obtain the following derivative
, obviously, when k is a positive constant, it represents a sphere, which is labeled as E. By calculating we obtain the following derivative
![]() (4)
(4)
Obviously, ![]() represents an ellipsoid in H, which is labeled as C. From (4) we know that
represents an ellipsoid in H, which is labeled as C. From (4) we know that ![]() on outside of C,
on outside of C, ![]() on C, and
on C, and ![]() inside of C. If k is big enough, E will include C. Therefore, from (4) we know that
inside of C. If k is big enough, E will include C. Therefore, from (4) we know that![]() ,
, ![]() on outside of C. From the Liapunov
on outside of C. From the Liapunov
theory we know that the orbits of system (1) will enter E. Namely E is the trapping region of the equations (1). Though the stationary solutions![]() ,
, ![]() , and
, and ![]() are all unstable, the system (1) still has the global stability, orbits of system (1) contract into the trapping region and oscillates in the trapping region. Finally the orbits form an invariant set in the trapping region, which is called the strange attractor.
are all unstable, the system (1) still has the global stability, orbits of system (1) contract into the trapping region and oscillates in the trapping region. Finally the orbits form an invariant set in the trapping region, which is called the strange attractor.
4. Numerical Simulation
In this section we present the numerical experiment results.
1) For Re < R3 = 52.785…, the stationary solutions ![]() of system (1) is stable, Numerical evidences indicate that any randomly chosen initial data is attracted by one of them, so they are global attractors.
of system (1) is stable, Numerical evidences indicate that any randomly chosen initial data is attracted by one of them, so they are global attractors.
2) At Re = R3 = 52.785… the four stable stationary solutions ![]() become unstable because a pair of complex conjugate eigenvalues of Jacobian matrix at stationary point crosses the imaginary axis, each of the four stable fixed points generated by the preceding bifurcations loses stability undergoing a Hopf bifurcation, and each generates a stable periodic orbit (hence foursymmetric orbits
become unstable because a pair of complex conjugate eigenvalues of Jacobian matrix at stationary point crosses the imaginary axis, each of the four stable fixed points generated by the preceding bifurcations loses stability undergoing a Hopf bifurcation, and each generates a stable periodic orbit (hence foursymmetric orbits ![]() are generated), and four stable periodic orbits around the fixed points
are generated), and four stable periodic orbits around the fixed points ![]() arise via a Hopf bifurcation (Figure 1) are stable up to Re = R4 = 55.36 ∙∙∙ and numerical results shows that they attract any point chosen at random.
arise via a Hopf bifurcation (Figure 1) are stable up to Re = R4 = 55.36 ∙∙∙ and numerical results shows that they attract any point chosen at random.
3) At Re = R4 = 55.36 ∙∙∙, the periodic orbits lose stability. As predicted by the general theory of bifurcation [7], Numerical evidences indicate that each one of the periodic orbit gives rise to a new periodic orbit, the new orbits are very similar in shape to the previous ones, only they wind up twice (Figure 2). With the increasing of
the Reynolds number Re, the number of periodic orbits also increases, the computer simulation shows that other similar bifurcations take place at Re = R5 = 55.365 ∙∙∙, Re = R6 = 55.40 ∙∙∙ and Re = R7 = 55.60 ∙∙∙, each time the new orbits wind up around the fixed points twice, at this point, the system is in a state of quasi-periodic. the sequence of period doubling bifurcations should accumulate (according to Feigenbaum’s theory); in another region of phase space a pair of periodic orbits ![]() (one stable and one unstable) are created, therefore, a hysteresis (i.e., coexistence of attractors) phenomenon appears.
(one stable and one unstable) are created, therefore, a hysteresis (i.e., coexistence of attractors) phenomenon appears.
4) As discussed above, at Re = R7 = 55.64 ∙∙∙, a new kind of periodic orbit appears. Each of the previous four orbits bifurcates into anew orbit, the new orbits wind up around two of the fixed points![]() , instead of only one like the previous ones. More precisely there are two orbits winding around
, instead of only one like the previous ones. More precisely there are two orbits winding around ![]() and
and ![]() and the other two around
and the other two around ![]() and
and ![]() (one stable and one unstable) (Figure 3).
(one stable and one unstable) (Figure 3).
The attraction basin of the stable periodic orbit rapidly extends, as Re grows within a very small interval. While Re in this interval a hysteresis phenomenon occurs and some initial data are attracted by the new stable orbit and others are attracted by the doubling periodic orbits (see Figure 3). Soon the attraction basin of the new orbit appears to swallow the region where the doubling periodic should be located. A “collision chaos” seems to take place.
5) The stable periodic orbit become unstable at Re = R8 = 55.76 ∙∙∙, increasing Re we have a sequence of bifurcations in which each time the period doubles and the number of loops around each fixed point doubles. We found four further bifurcation points of such nature, for the following values of Re:Re ; 55.80..., Re ; 55.84, Re ; 55.92. Since the period doubles each time and the orbits become increasingly intricate requiring higher precision, we did not look for further bifurcations. So we cannot definitely state whether we have just a finite number of bifurcations and the only obstacle to observe more seems to be the numerical precision needed, then the strange attractor appears, namely, the period doubling bifurcations transition into chaos (Figure 4 & Figure 5).
6) Figure 6 shows bifurcation diagrams of the system (1). Figure 7 shows the corresponding largest Lyapunov exponents. The periodic motions generated by the period doubling bifurcation continue to double in ever faster succession (as Re grows) eventually generating a chaotic attracting set. Moreover, these bifurcation diagrams show self similarity.
7) Figures 8-10 show Poincare section, return map and power spectrum of the system (1) at Re = 57.95. They indicate chaos feature of the new system (1).
8) From bifurcation diagrams Figure 7, we find that the chaotic region contains periodic-orbit windows of
varying width, the strange attractors and limit cycles appear alternately at some Reynolds number. Through more delicate and difficult calculation we obtain the following details: at Re = 58.88... the strange attractor shrinks into a symmetrical limit cycles (Figure 11), at Re = 59.90..., the limit cycles become unstable and the periodic orbits generated by the period doubling bifurcation continue to double in ever faster succession eventually generating a chaotic attracting set (Figure 11). At Re = 68.48..., the strange attractor shrinks into a symmetrical limit cycles again, if followed backwards with decreasing Re, this bifurcation is an “inverse” bifurcation.
5. Conclusion
This paper has presented and studied a five-mode Lorenz-like system of the Navier-stokes equations for a two- dimensional incompressible fluid on a torus. Dynamical behaviors of this new chaotic system, including some basic dynamical properties, bifurcations, and routes to chaos, etc., have been investigated both theoretically and numerically by changing Reynolds number. We have found period-doubling bifurcations to chaos, intermittent scenario, periodic windows, hysteresis and coexistence of periodic attractors. The chaotic behavior was discussed with the aid of bifurcation diagram, Lyapunov exponent spectrum, Poincare section, power spectrum and return map. Furthermore, the existence of attractor and the global stability of the equations have been firmly verified and our theories and methods can be used in other similar systems.
Acknowledgements
We thank the editor and the referee for their comments. Research works are subsidized by the National Nature Science Foundation of China (11572146), the funds for education department of Liaoning Province (L2013248) and science and technology funds of Jinzhou city (13A1D32).