Decay of Pressure Fluctuation in the Hyporheic Zone around a Cylinder ()
Received 17 February 2016; accepted 26 April 2016; published 29 April 2016

1. Introduction
Many sediment transport problems are empirically approached using sediment transport equations with a large amount of uncertainty. One such problem is local scour around bridge piers. Local accelerations in river velocity increase the ability for a river to erode sediment. Bridge support structures at river crossings create local acceleration. Removing enough sediment from the river bottom near bridge piers or abutments can cause the bridge to become unstable, increasing the risk of failure. Over the last few decades, statistical and physical modeling dominated scour research with the goal of relating hydrodynamics, geometry and sediment data to scour depth. In practice, scour, as well as other sediment transport processes are estimated with empirical equations with functional forms dependent on surficial processes and geometry. The goals of this work are to measure patterns of pressure fluctuations below the sand-water interface in three positions around a cylinder (0, 45 and 90 degrees relative to the stream wise flow direction) and use it to describe how pressure fluctuations change with depth and modify an existing formula describing these fluctuations as a function of depth.
Understanding the intricacies of sediment transport and incipient motion requires knowledge of forces applied to individual particles. Multiple studies exist measuring pressures in the interstices of gravel and relate it to sediment transport [1] , [2] and to some extent [3] . However, this is the first known investigation into hyporheic pressure fluctuation decay in uniform sand. This study uses a vertical cylinder to house pressure sensors measuring fluctuation decay through the upper 15 mm of sand. The cylinder helps overcome the practical limitations of measuring within the interstial space of the sandy matrix and by its presence lends itself to future bridge scour applications.
The focus of the investigation is two-fold: first, use the synchronous measurement of velocity and the hyporheic pressure field around a vertical cylinder to adapt existing pressure fluctuation decay equations. The modified equation is for applications in unimodal sediment where a circular hydraulic structure is present. Second, describe and compare the distribution of hyporheic pressure fluctuation at three radial locations around the cylinder.
Under favorable conditions, subsurface pressure fields reduce the apparent weight on individual particles, destabilizing and mobilizing the bed. This occurs when localized zones of high-pressure fluctuation develop in a relatively deep stratum while a localized zone of low-pressure fluctuation appears in a more elevated stratum [4] . Fluid velocity and pressure are jointly responsible for the hydrodynamic forces leading to erosion of particles [2] . It is necessary to understand this joint relationship to gain a detailed understanding of the mechanisms contributing to bed instabilities [2] . Knowledge of these forces and their origin increases the understanding of erosion on a particle scale.
The present experimental design positions the pressure sensors inside the cylinder and below the water-sand interface, eliminating the disturbance of flow around the cylinder. Since flow around a cylinder is already well studied, theoretical results and previous experiments are used to help validate this work.
2. Methods
The experimental portion of the project comprised nine experimental runs to capture sub-surface pressure fluctuations around a vertical cylinder. Experiments gathered data at three radial locations around the cylinder. The pressure ports on the cylinder were aligned at 0-degrees, 45-degrees and 90-degrees relative to the longitudinal centerline of the flume. Three trials were conducted for each alignment. The cylinder was placed approximately 7 meters from the head of the flume. Synchronous near-bed velocities and subsurface pore-water pressure measurements were recorded at three different elevations on the cylinder at each sampling location, radially spaced at 0, 45, and 90-degrees from the stream wise orientation as shown in Figure 1 around the cylinder. The three sampling elevations were spaced at 6 mm (on center) vertical increments over a total depth of 15 mm in the sand bed, Figure 2.
The low-pressure port for pressure sensor three was fully exposed to the flow (i.e. it was at the sand/water interface but fully above it) at the start of the experiment, Figure 2. Grains moved during the course of the experiment but not enough to expose the high-pressure port on sensor three. Based on the Hjulstrom curve [5] , velocity in the flume upstream of the cylinder was 66-percent of the critical velocity required to entrain the median particle diameter. Based on the Shields’ diagram [6] , the shear upstream of the pier was approximately 81-percent of the critical shear.
This research used differential, dry-gas pressure sensors from Sensor Technics®. The pressure sensors output a zero-to-five volt analog signal corresponding to a differential pressure head of zero-to-five inches of water. The pressure sensors have an associated accuracy of 0.6% full scale or 0.8mm of water. The dry gas pressure sensors were mounted in a box above the flume and connected to the cylinder with flexible Tygon® tubing with an inside diameter of 3 mm (6 mm outside diameter). The pressure sensors were connected to the cylinder in two columns: a high-pressure side and a low-pressure side, sampled at 1000 Hertz and smoothed with a moving average with period of 100 samples. Figure 3(a) shows the pressure sensors and 3b the mounting assembly.
![]()
Figure 1. Flume plan view schematic showing the locations of the pressure measurements relative to the flow. For each location (0, 45 and 90) three pressure sensors were vertically mounted 6 mm on center through the first 15 mm of sand.
![]()
Figure 2. Differential pressure sensor configuration on the cylinder. Low pressure ports are on the right, high pressure ports are on the left.
![]()
![]() (a) (b)
(a) (b)
Figure 3. (a) Pressure sensor; (b) Pressure sensor assembly.
A Nortek Vectrino II® down-looking profiler was used to measure three dimensional velocity components around the cylinder at a sampling frequency of 100 Hz. Velocities were collected as close to the cylinder as possible. Accommodating the geometry of the probe head required approximately 30 mm of horizontal space between the cylinder and the center of the sample volume. Velocities were collected over 30 mm range in the vertical at 1 mm resolution. A Gaussian filter was applied to both the velocity and pressure time series to remove outliers. When a velocity or pressure difference was determined an outlier, it was removed from the time series and a cubic polynomial was used to interpolate these missing data, this affected less than three percent of all measurements. Prior to the cylinder being placed in the flume, the friction velocity, Uτ, was determined using the method described by [7] . Velocities were collected from 0.2 < y/δ < 1 where δ is the thickness of the boundary layer and y is the distance above the bed.
Three trials were conducted for each pressure port orientation (0, 45 and 90 degrees). Identical flow conditions were used for all nine experiments. Velocity and pressure measurements were recorded for five minute trials. Spectral densities of each signal were examined with the Welch method [8] using 50-percent overlap.
This research was conducted in a 91 cm wide, 13-meter long flume. The flume has clear acrylic sides and an engineered plywood bottom. A 60 Hz variable speed pump and a 20,000 liter reservoir supply water to the flume. The flume has a flow straightener, elevated sediment test section and a v-notch weir to control the flow (Figure 4). Sand and velocity characteristics for all runs are shown in Table 1; U is the stream wise velocity, Uc is the critical velocity for particle entrainment, Uτ is the friction velocity and d50 is the median grain size diameter. A uniform, angular, sand with mean sediment size (d50) of 0.85 mm and uniformity coefficient of 1.4 was used in this experiment. The grain size distribution is provided in Figure 5.
![]()
Table 1. Flow and flume characteristics.
3. Results
Velocities were carefully measured and velocity distribution parameters determined with the Krogstad fit were compared to expected values, [7] . In this study, the friction velocity was determined to be 0.0198 m/s while the measured free stream velocity was 0.20 m/s. While the Krogstad method requires assignment of velocity at zero distance above the channel bed, this is especially difficult to estimate for rough beds. The Krogstad procedure also determines the velocity shift (ε) associated with a rough bed. This shift is a vertical displacement of the velocity profile and accounts for the distance between the plane of zero velocity and the top of roughened surface where the velocity is not quite zero. Values of ε/k, where k is the roughness height, are expected to be less than 0.3 over rough, impermeable beds [9] . Applying the Krogstad fit to the results of this investigation, the ε/k value is calculated as 0.16. However, the bed in the present case is permeable. Reference [10] notes that permeable beds alter the expected range of parameters suggested in literature for log-law fits of data when compared to those measured over impermeable beds.
The Strouhal number is a dimensionless parameter important in oscillating flows [11] . It is defined as
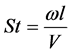 (1)
(1)
where St is the Strouhal number, ω is the frequency of oscillation associated with vortex shedding, l is the characteristic length (diameter of cylinder) and v is the average velocity. At high Reynolds numbers, the Strouhal number is 0.21 for flow around a cylinder [11] . For the given flow condition, the Strouhal Equation (1) predicts an oscillating frequency of 0.38 Hertz. The measured pressure and velocity spectra of Figure 6 suggest peaks between 0.35 and 0.45 Hertz-corresponding well with the theoretical value.
The characteristics of subsurface pressure fluctuations change with radial position and depth. Figure 7 shows the standard deviation of the pressure fluctuations as a function of depth of cover. At all radial locations, the intensity of the pressure fluctuations decrease with depth as seen in Figure 7. Each point represents the standard deviation of approximately 30,000 measurements of pressure.
Several investigators, including [12] - [14] , reported that the root mean square of the pressure fluctuations at the bed, ith out the presence of a structure, is approximately three times the boundary shear stress for the smooth or rough flat bed case. In the present investigation, pressure sensor three is 3mm beneath the surface of the sand/water interface and is useful for comparisons between near-bed pressures and shear stress similar to those by [4] . Based on data from the present study for the 0- and 45-degree alignments, the root mean square of the
pressure fluctuations is approximately seven times larger than the boundary shear stress.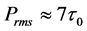 . For the 90- degree location
. For the 90- degree location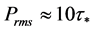 .
.
4. Discussion
4.1. Equation Development
The present investigation seeks to adapt an equation to describe the decay in the magnitude of pressure fluctuations as a function of depth below the water/sand interface for a given flow condition around a cylinder. The starting point for this work is based on current literature describing the decay, absent any hydraulic structure, as exponential [1] , [10] and [15] .
Reference [1] describes the decay inside a permeable wall (bed) with the general exponential function shown in Equation (2)
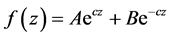 (2)
(2)
where z is the depth of cover and c is a wave number associated with the structure of the flow. Equation (2) is a generalized solution to the Navier-Stokes Equation for flow within a granular layer [1] . The positive portion of
![]()
Figure 6. Spectral analysis shows connectedness of the surface pressure and the velocity data. Both velocity and pressure spectra have spikes at about 0.4 Hz which corresponds well to the Strouhal predicted value of 0.38 Hz.
![]()
Figure 7. Pressure fluctuation as a function of depth for all three locations and all three depths for each trial using Equation (4).
Equation (2) has no physical meaning and [1] suggest truncating it and using the first term only. [10] , show that inside a permeable wall with homogeneous porosity, the Reynolds-averaged Navier-Stokes equation is solved with an exponential decay function. [10] parameterizes the decay based on porosity and wall permeability. [15] adopt the exponential function in Equation 3 to describe pressure fluctuation decay through a bi-modal sediment mixture, Equation (3).
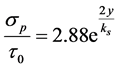 (3)
(3)
In the present work, Equation (3) was adapted to describe pressure fluctuation decay as a function of depth of cover in the presence of a vertical cylinder and unimodal sand. The Detert and Parker equation (Equation (3)) was used as the foundation for this development. However, there are some notable differences between the conditions of the present investigation and those of the Detert and Parker investigation that resulted in Equation 3. The Detert and Parker investigations used bimodal bed material, while the present experiments took place in a sand bed with uniform grain size distribution. The present study included a cylinder in the flow field while the Detert and Parker work used an unobstructed flow field. Since the present work used uniform grain size, the equivalent grain size appearing in Equation (3) was changed to the median grain size 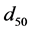 in the current adaption. To address the differences between previous and current research, modified coefficients were determined to adapt Equation (3) for use in uniform sediment and near a cylindrical structure.
in the current adaption. To address the differences between previous and current research, modified coefficients were determined to adapt Equation (3) for use in uniform sediment and near a cylindrical structure.
![]() (4)
(4)
where ![]() is the standard deviation of the pressure fluctuations where
is the standard deviation of the pressure fluctuations where ![]() acts as an indicator of fluctuating lift, [15] ;
acts as an indicator of fluctuating lift, [15] ; ![]() is the boundary shear stress; b is the regression coefficient; is the depth of cover (negative value);
is the boundary shear stress; b is the regression coefficient; is the depth of cover (negative value);
d50 is the median grain size; The relationship expressed by Equation (4) is shown alongside the measured values in Figure 7. The best-fit parameters for Equation 4 as determined from the experiments of this investigation are provided in Table 2.
4.2. Pressure Distribution
When instantaneous pressure fluctuations above a particle are reduced relative to the average differential pressure at the same point, the particle requires a reduced shear to initiate motion. These measurements define the pressure distribution at the surface as well as through the first several millimeters of sand. The subsurface pressure distributions change with radial position and depth of cover; however, at all radial locations, the intensity of the pressure fluctuations decreases with depth as seen in Figure 7. In general, the pressure fluctuations recorded at the deepest probes are normally distributed, but the shape of the distribution changes with depth and radial position as discussed below.
Pressure sensors located at a 0-degree alignment had an approximate normal distribution at all depths as shown in Figure 8. Pressure sensor one is 15 mm below the sand surface. The measured pressure fluctuations at sensors two and three, 9 mm and 3 mm below the surface respectively, show small deviations from normal in the tails. Similarly, at the 45-degree location, pressure sensor one, has an approximate normal distribution; however, pressure sensors two and three show a deviation from normal in the tails and have negative skew, Figure 8. In the 90-degree position, the pressures recorded at the deepest pressure sensor 15 mm beneath the sand-water interface are again approximately normally distributed; however, the pressures recorded at pressure sensors two and three exhibit bimodal behavior. This behavior is explained by periodic vortex shedding associated
![]()
Table 2. Regression coefficients, mean square error and R-squared for fits to Equation (4).
![]()
Figure 8. Normal probability plots for each pressure sensor at each radial location.
with flow around a cylinder and described by [16] . Periodicity is seen in the pressure signal due to the placement of the pressure ports flush with the surface of the cylinder. However, due to the 30 mm offset between the cylinder and the in this investigation, bimodal behavior was not detected in the velocity measurements.
5. Conclusions
This work helps understand how fluctuating pressure fields, in the presence of cylinders, interact with and decay through the hyporheic zone. Previous investigations incorporated the forces on particles due to hyporheic process only for the case of materials with relatively high hydraulic conductivity and coarse size fraction (gravels), and only in flat beds with no flow obstruction. The present investigations clearly document the ability to measure and quantify hyporheic pressure fluctuations for much finer material and in the presence of a hydraulic structure. These fluctuations play an important role in the force balance associated with incipient motion of individual grains and these measurements help identify the processes responsible for generating additional lift.
Subsurface pressure fluctuations were measured and used to modify existing functions describing pressure fluctuations in the hyporheic zone; however, models were modified to better reflect the processes specific to this research such as the inclusion of a circular cylinder. The modeled data clearly follow the exponential decay model proposed by [1] [10] [15] . These data represent the first time subsurface pressure fluctuations were measured in the presence of a hydraulic structure and help broaden the application of previous developed models. However, further investigation is required into mixed grain-size sediment as well as blockage ratios.
Notation
The following symbols are used in this paper:
Prms root mean square of pressure fluctuation
St Strouhal Number
U stream wise velocity
Uc critical velocity for particle entrainment
Uτ friction velocity
V average velocity
bi regression parameter
c wave number
d50 median grain size
k roughness height
l characteristic length, diameter of cylinder
Uτ friction velocity
y distance above the bed
z depth of cover
δ boundary layer thickness
ε shift in velocity origin associated with rough bed
σp Standard deviation of pressure fluctuations
τ0 boundary shear stress
ω frequency of vortex shedding off the cylinder
NOTES
![]()
*Corresponding author.