Received 14 March 2016; accepted 17 April 2016; published 20 April 2016

1. Introduction
The financial crisis of 2008 has done a great damage to the global economy, and the procyclicality of financial system and capital regulation are regarded as the two most important reasons that lead to the financial crisis. Under this background, Basel III was released, which implies more stringent requirements for financial institutions. The countercyclical capital buffer is one of the most important parts of the new regulatory framework, which aims to enhance the stability of the banking system in different business cycles. Capital buffer is the excess capital held by banks. The positive relationship between capital buffer and business cycles is defined as countercyclicality.
After the financial crisis, the issue of the cyclicality of capital buffer has been the subject of much investigation. There are lots of scholars doing empirical studies about the effects of ownership, capital regulation, and bank size on bank capital buffer. But there is little study on the relationship between market structure and the cyclicality of capital buffer. These years lots of regulation has been implemented in Chinese banking sector and the banking market concentration is decreasing. The China Banking Regulatory Commission (CBRC) is trying to establish countercyclical regulatory framework for Chinese financial system. Therefore, studying the relationship between market structure and the capital buffer helps the regulatory authorities make more suitable countercyclical regulatory policies. According to our knowledge, this is the first paper that uses the database of Chinese banks to examine the relationship among business cycle, banking market structure and capital buffer. The empirical results reveal that capital buffers are positive to business cycle, which is different from that of studies on Western economies. And the decrease of banking sector concentration intensifies the countercyclical behavior of capital buffers. The results may motivate supervisory authorities to consider banking market structure when implementing countercyclical regulatory policies. The rest of the paper is organized as follows. Section 2 introduces the review of academic literature. Section 3 shows the methodology and the econometric results. Section 4 is the robust checks. Finally, Section 5 presents our conclusion.
2. Review of the Academic Literature
Capital buffer is defined as the gap between the real capital ratio and the regulatory requirement. Banks hold capital buffer for three reasons: 1) Banks may hold capital buffer to signal soundness to the market and reduce the information asymmetry between banks and the market. 2) Banks keep capital buffer as an insurance against the violation of the minimum capital requirement and the adverse shocks. 3) To catch the unexpected investment opportunities in the future, thus put banks in a competitive position.
As for the relationship between business cycle and capital buffer, the studies didn’t reach an agreement. Most papers hold the opinion that capital buffers take on negative co-movements with business cycles. In empirical study, Ayuso et al. [1] firstly study the cyclical behavior of capital buffers in Spanish banking sector. The results reveal that the capital buffers are significantly negative to the business cycle, which indicates that the capital buffers are procyclical. Based on the study of Ayuso et al. Lindquist [2] uses the bank-level panel data in Norway from 1995-2001 and finds that capital buffer is positive to the competitors’ capital buffer and the capital buffers of banks with low capital ratio exhibit more procyclical. Tabak et al. [3] use a panel data of Brazilian institutions from 2000 to 2010 to estimate the relationship between business cycle and capital buffer, the results show that capital buffers exhibit negative co-movement with the economic cycle. Coffinet et al. [4] find that the capital buffers of French banking sector are also procyclical. Shim [5] tests the cyclical behavior of banks’ capital buffers in America and reaches the same results.
However, some papers report different results. Jokipii and Milne [6] find that capital buffers of RAM10 are countercyclical, and capital buffers of the EU15 are pro-cyclical. Fonseca and Gonzalez [7] use an international sample of 2361 banks from 92 countries to analyze the cyclicality of bank capital buffers. The results suggest that the cyclical effects of capital buffers are different in different countries. The results of Carvallo et al. [8] show that there is a significantly negative relationship between capital buffers and GDP growth for five countries, while positive and significant for six, using the data of banking sectors of 13 Latin American and Caribbean countries for the period 2001-2012.
Previous studies tried to study the impact of some characteristics, like ownership structure, bank size or the regulatory policy on the cyclical behavior of bank capital buffers. However, banking market structure may also influence the behavior of bank capital buffers. In high concentrated market, banks may have market power to obtain more profits, thus they will tend to hold more capital buffer [9] . Saunders and Wilson [10] find that during economic upturns in the United States of America, banks with greater market power operated with lower leverage, thus banks may hold higher capital. Ruckes [11] , Jimenez and Saurina [12] suggest that competition induce banks to take looser loan policy, which will increase the risk-weighted risks and lower the capital buffer. The competition is negative to the market concentration. Therefore, the market concentration positively related to the capital buffer. Saadaoui [13] find that concentrated structure may enhance market power and the market power attenuates the negative relationship between business cycle and bank capital buffer. Thus, market concentration enforces the procyclicality of capital buffer. However, to our knowledge, there is no empirical study on the relationship between the banking market structure and capital buffer in Chinese banking sector. Therefore, this paper will contribute to the literature on the cyclical behavior of capital buffer in several ways. First, we empirically study the relationship between market structure and capital buffer. Second, we test the effects of banking market structure on the cyclical behavior of capital buffer. Finally, we analyze the driving force of the cyclical effects.
3. Empirical Study
3.1. Empirical Model
According to previous studies as Ayuso et al. [1] and Shim [5] , Equation (1) is established to examine the cyclicality of capital buffer and the relationship between capital buffer and the banking market structure.
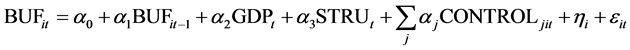 (1)
(1)
where BUF is the capital buffer; GDP denotes the growth rate of gross domestic product; STRU is the market concentration and we use CR4, HHI to measure the market concentration respectively. Variables CR4 and HHI are widely used to measure concentration in the banking sector. CR4 is given by the loan of the four largest banks as a share of loan of all commercial banks. HHI is the Herfindahl-Hirschman index and defined as the sum of squared market shares. CONTROL represents control variables, including SIZE, ROE, GLOAN, NPL, and ROA.
 (2)
(2)
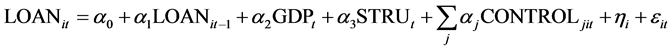 . (3)
. (3)
Capital buffer adjustment can be divided into the denominator and numerator effects. The denominator effect implies that banks adjust risk-weighted assets to change capital buffer. The numerator effect indicates that banks adjust net capital to change the level of capital buffer. Equations (2) and (3) are respectively established to examine the two preceding effects.
The control variables in Equations (2) and (3) are the same as those in Equation (1). As it is difficult to get the data of net capital and risk-weighted assets, we choose capital and loan to substitute for net capital and risk- weighted assets. In Equation (2), CAP represents the ratio of capital to total assets. In Equation (3), LOAN represents the ratio of loan to total assets.
3.2. Methodology and Data
Equations (1) to (3) contain the first-order lagged terms of the explanatory variable. Given the dynamic panel structure of the models, we employ the generalized method of moments (GMM) estimator. According to Blundell and Bond [14] we use the one-step system GMM in order to avoid the endogeneity and the weak instrument problem.
Our dataset consists of 40 Chinese commercial banks from 2004 to 2014, including 5 State-owned banks, 11stock or joint-equity banks and 24 urban commercial banks. The sample covers almost 65.9% percent of assets of Chinese banking sector. We get the bank-level data from the annual reports of commercial banks and the Wind, a database containing detailed accounts and information of Chinese financial institutions. The macroeconomic data are from the China Statistical Yearbook and the website of the People’s Bank of China. The descriptive statistics of sample data are presented in Table 1. From Table 1, we can see that the average capital buffer of Chinese banking sector is 3.366%, ranging from −9.47 to 22.67. And the market concentration of Chinese banking sector is decreasing.
3.3. Empirical Results
3.3.1. Business Cycle and the Behavior of Bank Capital Buffer
The coefficients of lagged terms [BUF (−1)], [(CAP (−1)], and [LOAN (−1)] are all significant. Thus, the establishment of the dynamic panel model is reasonable. Column 1 and 2 of Table 2 present the results of Equation (1). With respect to GDP, we find a positive coefficient and it is significant, which indicates that bank capital buffers fluctuate countercyclicality. Then we analyze the driving sources of the countercyclicality. We test two components: the bank capital and credit assets. Column 3 and 4 of Table 2 are the results of Equation (2). The results suggest that GDP is positive to the bank capital which means that the behavior of bank capital is countercyclical. Column 5 and 6 of Table 2 are the results of Equation (3). In the LOAN equation, GDP is negative to the credit assets, which means that the credits assets are also countercyclical. Therefore, both bank capital and
![]()
Table 1. Descriptive statistics of indicators.
![]()
Table 2. Main results of the estimation of Equations (1)-(3).
Note: Numbers in parentheses are t-values. *, **, and *** denote statistical significance at the 10%, 5%, and 1% confidence levels.
credit assets are driving factors of the countercyclical behavior of bank capital buffers.
In BUF equation, GLOAN is significantly negative to BUF, showing that banks’ credit growth influences the change of capital buffer. NPL is negative to BUF, indicating that the increasing of risk will lead to the decreasing of capital buffer. ROA is positive to BUF, because the banks with high profits will be easier to increase capital through retained earnings. ROE is negative to BUF, when the cost of holding capital buffer increases, the banks will decrease the level of capital buffer. SIZE is negative to BUF, but not significant.
3.3.2. Banking Market Structure and Capital Buffer
In the first column of Table 2, we find that CR4 is significantly negative to capital buffer. In the second column of Table 2, we find that HHI is also negatively related to capital buffer. The results show that the decrease in banking sector concentration will help to increase banks’ capital buffers. From the column (3)-(6) of Table 2, we can see that the coefficients of CR4 and HHI are negative in CAP equation which indicates that the decrease in market concentration will lead to the increase in bank capital .Because when the competition becomes fierce, the banks may take more stable strategy. In the LOAN equation, CR4 and HHI are positive to loan, which implies that with the increase of banking sector concentration, the credit growth will accelerate. The decrease of market concentration will induce banks to increase the level of capital and decrease the credit assets, thus leading the level of banks capital buffer to increase.
3.3.3. Effect of Banking Market Structure on Cyclicality of Capital Buffer
In order to test whether market concentration affects the cyclicality of bank capital buffers, we add to equation (1) the interacting variables CR4*GDP and HHI*GDP respectively. In the first column of Table 3 the coefficient of CR4*GDP is negative and statistically significant. In the second column of Table 3 we can also see that HHI*GDP is significantly negative to bank capital buffer. The results show that the decrease in bank market concentration will intensify the countercyclical effects of capital buffer. In the CAP and LOAN equations, we see that CR4*GDP and HHI*GDP is negative to the bank capital, positive to the loan, which suggest that the decrease in the banking market concentration will intensify the countercyclicality of bank capital and loan.
![]()
Table 3. Effect of banking market structure on cyclicality of capital buffer.
Therefore, with the implementation of reform in Chinese financial system and the opening-up of financial market in China, Chinese banking market concentration is decreasing and it is benefit to the development and stability of Chinese financial system.
4. Robustness Checks
We run pooled OLS and fixed effects estimations as a robustness check. The reason for doing so is that studies show that the OLS estimator is biased upward, while the FE estimator is biased downward [15] . So the GMM estimates lie in between the OLS and FE estimates. We use both pooled OLS and fixed effect model to test all the equations. All of the coefficients of the first-order lag in this paper satisfy the preceding requirements,1 which indicates that our empirical results are robust.
5. Conclusion and Policy Suggestions
This paper analyzes the relationship among business cycle, banking market structure and capital buffers by using a dataset of 40 Chinese commercial banks from 2004 to 2014. The results show that in China: the behavior of capital buffers are countercyclical, and market concentration shows a negative relationship with the capital buffers. The decrease of market concentration enforces the countercyclical behavior of capital buffers.
Our results have important implications for policymakers. 1) Different from western banking sector, the behavior of Chinese bank capital buffers is countercyclical, which is benefit to the stability of the financial system. 2) The Basel III is enacted based on the procyclicality of financial system, so when we introduce the Basel III to Chinese financial system, we should make some changes and take the current situation of Chinese banking sector into consideration. 3) Market concentration is an important factor that will affect the capital buffers. When the policymakers make regulatory policies, it is necessary to consider the market structure in implementing countercyclical capital standards. 4) New financing channels should be explored to help banks to replenish capital.
NOTES
![]()
1Relevant results are available upon request.