Influence of Slope Angle on the Walking of Passive Dynamic Biped Robot ()
1. Introduction
Human walking can be considered as a complex mechanical process controlled by Newton’s law of motion which inspired to model the biped robot. Furthermore, the biped robot is more capable to work in the hazardous atmosphere than the wheeled vehicles. The fundamental problem of biped robot is to achieve the stable gait but it is not a trivial task. So, most of the researchers have focused on locomotion while working on bipedal robots till today. We will mainly focus on the walking pattern of robots. This paper will discuss about the effect of slope on the behavior of robot while walking on the inclined ramp.
This paper organized in several steps. Section 2 presents mathematical model of passive dynamic knee-less biped robot, powered only by gravity while walking on the inclined ramp. The knee-less biped robot is built of two rods where rods are considered as the legs of biped while joint of rods is considered as a hip. The gait of biped is dividing into two phase: swing phase and impact phase. The motion of the swing phase is equivalent to the motion of double inverted pendulum [1] . The model has two basic parts: one is a differential equation for the swing motion and second is the impact function for the heel-strike when foot of swing leg touching the ground. The model build here is a representative of many biped models developed in the literature [2] - [7] .
Section 3 explains the basic definitions for the solution of discrete system which developed in Section 2 [8] - [10] . It also describes the method of poincare section to the system with consideration of impact effect [11] - [14] . The discrete-time map defines from the plane of Poincare section to itself, that is, physically define from one heel-strike to next successive heel-strike which is called poincare return map [15] - [17] . The fixed point analysis of the Poincare return map will generate the periodic motion of the system. One of difficult task to generate the periodic motion is the selection of initial condition which described in this section.
Section 4 describes the bifurcation route to chaos as an influence of slope angle [18] . The steps convergent sequences and phase space diagrams simply explain bifurcation theory. Section 5 gives the conclusion and scope of future work.
2. Modeling
This section presents the dynamic model of simplest passive biped robots, consisting two equal length rigid legs pivoted at the hip with no ankles and no knees. It is a structure of three point-masses: one at the hip and other two at the centre of mass of legs. These point masses are not independent due to the distance constraints imposed by the stance and the swing legs. So, the system has four degrees of freedom. The walk of robot is considered only in the sagittal plane and on a level surface. Furthermore, the a periodic motion consists of successive swing phases, means one leg (swing leg) is free for moving and other leg (stance leg) is touching the ground, and transition phase, means the transition from one leg to another taking place in an infinitesimal length of time [3] [8] . With this consideration, the model of the biped robot made up of two parts: the differential equations which describe the dynamics of the biped robot during the swing phase and the impact model which describe the contact event and transition phase. Such models are very common in the field of biped locomotion. The linearized form of this model will be used for further analysis. It is assumed that the biped has no foot scuffing and no bounce during the walking.
2.1. Motion Equation
The angular coordinates , masses
, masses  of the legs and hip, length parameters
of the legs and hip, length parameters  are indi-
are indi-
cated in Figure 1. Note that, the positive angles are calculated anticlockwise with respect to the indicated vertical lines in Figure 1. Moreover, it walks only under the gravity and all the external forces are absents. Using the Lagrange method [3] , the passive dynamic model of the robot between successive impacts is derived in a standard second order system
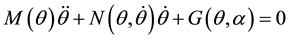 (1)
(1)
where :
: 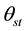 and
and 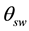 parameterize the angles of the stance leg and the swing leg respectively,
parameterize the angles of the stance leg and the swing leg respectively, 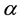 parameterize slope of a walking ramp. The matrix
parameterize slope of a walking ramp. The matrix 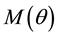 represents the inertia matrix, the matrix
represents the inertia matrix, the matrix
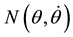 includes terms of centrifugal and coriolis forces,
includes terms of centrifugal and coriolis forces,  contains the gravity term are given as follows:
contains the gravity term are given as follows:
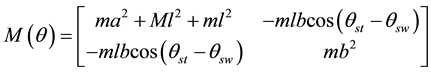 ;
;
![]() ;
;
![]() .
.
The effect of centrifugal and coriolis forces on the walk is very low so it can be ignored to find the walking pattern of a periodic motion of a biped robot. Neglecting the above forces, the non-linear Equation (1) formed into liearized equation,
![]() (2)
(2)
where ![]() is the equilibrium point. The state space form of the above linerized equations model can be written as
is the equilibrium point. The state space form of the above linerized equations model can be written as
![]() (3)
(3)
where the state space variable![]() ,
,![]() . The matrix
. The matrix ![]() is given as follows:
is given as follows:
![]()
where
![]() .
.
2.2. Impact Model
For the biped with equal length and without a knee, the identification of the point of contact of the swing leg with the walking surface would seem to be physically ambiguous because the swing leg must scuff along the ramp when it passes through the stance leg. It is assumed that the walker is prevented from the scuffing and the impact of the swing leg with the walking surface has no rebound and no slipping and stance leg naturally lifting from the ground without integration [2] [11] [12] . The impact between the swing leg and the ground is considered as a fully elastic collision between two rigid bodies [2] . At the time of impact, the vertical distance between foot of swing leg and the walking surface will become a zero, so it met the constraint![]() . Considering the elastic collision between the swing leg and the ground, the angular momentums are conserved at the foot of a swing leg and a hip indicated in Figure 2.
. Considering the elastic collision between the swing leg and the ground, the angular momentums are conserved at the foot of a swing leg and a hip indicated in Figure 2.
The conservation laws of the angular momentum gives to the following compressed equation between the pre- and post-impact angular velocities after the impact [3] which denoted by ![]() and
and ![]() respectively. Moreover, “-” and “+” represent the left and right limits respectively.
respectively. Moreover, “-” and “+” represent the left and right limits respectively.
![]()
![]()
Figure 2. Orientation of the angular momentums of the swing leg’s foot before and after the impact are displayed by the blue lines and for the hip, it displayed by the green lines.
where![]() ,
,![]() ;
; ![]() and
and ![]() .
.
After the impact the swing leg will be the new stance and the stance leg will be the new swing leg for the next subsequent step, it can be expressed by the following equation:
![]() .
.
The state space form of the impact model can be written as follows:
where
![]() (4)
(4)
2.3. The Complete Hybrid Model
The complete model of a biped passive dynamic robot is a hybrid of the motion equation and impact model which described as:
![]() (5)
(5)
where![]() . Figure 3 shows the walking steps of biped robot on the inclined ramp.
. Figure 3 shows the walking steps of biped robot on the inclined ramp.
Regarding this model, the evolution process of periodic motion of a walking robot is described in the following steps: first, a trajectory of the robot is evaluated by the solution of motion equation until an impact occurs. The impact occurs when attains the impact condition and generates a contact point on the walking ramp. As the result of impact, there is a very fast change in the velocity components of the state vector of the contact point which is done by the impact model. This instantaneous change in the velocity components is resulting in a discontinuity of the velocities which make the biped system discontinuous. The last result of the impact model is a new initial state of a robot for the evolution of next step until the next impact. Due to the instantaneous change at the time of impact, the robot have two different state space positions at the same time which not to be obliged, so the impact event is explained with two notation: first, the state vector “![]() ” at impact time “
” at impact time “![]() ” for the state just before impact and second, the state vector “
” for the state just before impact and second, the state vector “![]() ” at impact time “
” at impact time “![]() ” for the state just after impact.
” for the state just after impact.
3. Poincare Map and Analytic Solution
In this section, we define the poincare map for discontinuous system and describe the stability in sense of a fixed point of poincare map and describe the analytic solution of the impulse model (5).
![]()
Figure 3. Schematics show the steps of a periodic motion of a walking robot: Step I indicates the beginning of the walk, Step II indicates that swing leg swings until the next impact occur and Step III shows the impact of swing leg with the walking ramp.
3.1. Poincare Map
If we assume that the function ![]() is continuous where S is given the subset topology from Z, and then
is continuous where S is given the subset topology from Z, and then ![]() is an open subset of S. So The Poincare map
is an open subset of S. So The Poincare map ![]() define by
define by ![]() where
where
![]() is the solution of a continuous linear system (3) and
is the solution of a continuous linear system (3) and ![]() represents impact time with respect to initial state, is well define and continuous. With this notion of Poincare map the following statements hold for the linear sys-
represents impact time with respect to initial state, is well define and continuous. With this notion of Poincare map the following statements hold for the linear sys-
tem (5). (i) If ![]() is a periodic orbit of (5) that is transversal to S, then there exists a point
is a periodic orbit of (5) that is transversal to S, then there exists a point ![]() that generates
that generates![]() . (ii)
. (ii) ![]() is as table fixed point of
is as table fixed point of ![]() if, and only if, the orbit of
if, and only if, the orbit of ![]() is stable in the sense of Lyapunov. (iii)
is stable in the sense of Lyapunov. (iii) ![]() is an asymptotically stable fixed point of
is an asymptotically stable fixed point of ![]() if, and only if, the orbit of
if, and only if, the orbit of ![]() is asymptotically stable in the sense of Lyapunov [8] .
is asymptotically stable in the sense of Lyapunov [8] .
3.2. Analytic Solution of Linearized Equation of Motion and Proper Initial Condition
The analytic solution of linearized Equation (5) of motion is ![]() where
where ![]() is the initial condition of
is the initial condition of
walking. To get the stable walking, the initial condition should be proper otherwise random selection of initial conditions leads to walking falling forward or backward. To find the proper initial condition, considered the Poincare map of linearized model which is given by:
![]() .
.
The eigenvector y corresponding to unity eigenvalue of the matrix of Poincare map for some values of ![]() such that
such that ![]() and the corresponding slope angle can be found using the relation
and the corresponding slope angle can be found using the relation![]() .
.
This y could be the proper choice of initial conditions for some range of slope angle [3] .
4. Influence of Slope Angle on the Periodic Orbit
The state variable y, the half inter leg angle![]() , the step period
, the step period ![]() are focused to examine the influence of slope angle on the periodic orbit. The bifurcation diagram is the graphical evolutions of such variables as the function of slope angle
are focused to examine the influence of slope angle on the periodic orbit. The bifurcation diagram is the graphical evolutions of such variables as the function of slope angle![]() . We analyzed that the one periodic gaits turns
. We analyzed that the one periodic gaits turns ![]() periodic when slope angle is increased and further it directed to chaos. This research found that
periodic when slope angle is increased and further it directed to chaos. This research found that ![]() deg is the bifurcation point where the bifurcation occurs. The continuous spreading of points in the bifurcation diagrams represent the chaotic gaits, shown in Figures 4-6. We observed that the behavior of variables is monotonic during the period doubling flow. The following table details the behavior of the biped robot during a period doubling flow as the influenced of slope angle α.
deg is the bifurcation point where the bifurcation occurs. The continuous spreading of points in the bifurcation diagrams represent the chaotic gaits, shown in Figures 4-6. We observed that the behavior of variables is monotonic during the period doubling flow. The following table details the behavior of the biped robot during a period doubling flow as the influenced of slope angle α.
Analyzing Table 1, the intervals of slope angle ![]() are gradually decreasing for
are gradually decreasing for ![]() periodic orbit. 8-periodic orbits are very sensitive so it difficult to observed, shown in Figure 10 and after that number of bifurcations are occurred for small change in the value of slope angle
periodic orbit. 8-periodic orbits are very sensitive so it difficult to observed, shown in Figure 10 and after that number of bifurcations are occurred for small change in the value of slope angle ![]() but those bifurcations are difficult to separate individually.
but those bifurcations are difficult to separate individually.
The phase plane diagram can be used to show the period doubling flow. The 1 periodic gait occurs when the sequence of impact time converses to one point after some finite number of steps with respect to the initial condition, shown in Figure 7(a). In other words, after some finite steps from the initial conditions, the state va-
riables repeat themselves after every heel-stride i.e.![]() , so the phase plane diagram has only one
, so the phase plane diagram has only one
closed limit cycle which is identical to both legs, shown in Figure 7(b) [3] . For the 2-periodic gaits, the sequence of impact time has two convergent points after some finite number of steps with respect to the initial condition, shown in Figure 8(a), it means, after some finite steps, the state variables repeat themselves after two
successive heel-strike:![]() . As a result, the phase plane diagram generates two closed limit cycles
. As a result, the phase plane diagram generates two closed limit cycles
each one is associated to one leg, shown in Figure 8(b) [3] . In case of 4-periodic gaits, the sequence of impact time has four convergent points, shown in Figure 9(a) and the state variables repeat themselves after 4 steps. Consequently, the phase plane has four closed limit cycles where each leg is associated two closed limit cycles, shown in Figure 9(b) [3] . Also in case of 8-periodic gaits, the sequence of impact time has eight convergent points Figure 10(a) and the phase space plane has eight closed limit cycles where four for each leg, shown in Figure 10(b). In general, for ![]() -periodic gaits, each leg is associated to
-periodic gaits, each leg is associated to ![]() closed limit cycles in the phase plane [3] . In case of chaotic gait, difficult to find number of convergent points for the sequence of impact time, shown in Figure 11(a), so hard to separates the closed limit cycle associate to legs in the phase plane, shown in Figure 11(b) [3] .
closed limit cycles in the phase plane [3] . In case of chaotic gait, difficult to find number of convergent points for the sequence of impact time, shown in Figure 11(a), so hard to separates the closed limit cycle associate to legs in the phase plane, shown in Figure 11(b) [3] .
5. Conclusion and Future Scope
In this work, we analyzed the effect of slope angle on the stability of walking of passive dynamic biped robot on linearized model. From the results of bifurcation diagram, the stable walking range is obtained with respect to slope angle. Also we observed that the stability of walking of passive biped robot is deceased as the slope is increased. This linear model can be helpful for guessing the initial states of the robot for the stable walking of its nonlinear model. These results can be helpful for finding effect of slope angle on non-linearized model and also for designing a biped robot.
![]()
Table 1. Influence of slope angle on periodic orbit.
![]()
![]() (a) (b)
(a) (b)
Figure 7. 1-periodic limit cycles: (a) a diagram of impact time vs step numbers; (b) phase space diagram for ![]() deg. (---leg 1 and ---leg 2)
deg. (---leg 1 and ---leg 2)
![]()
![]() (a) (b)
(a) (b)
Figure 8. 2-periodic limit cycles: (a) a diagram of impact time vs step numbers; (b) phase space diagram for ![]() deg. (---leg 1 and ---leg 2)
deg. (---leg 1 and ---leg 2)
![]()
![]() (a) (b)
(a) (b)
Figure 9. 4-periodic limit cycles: (a) a diagram of impact time vs step numbers; (b) phase space diagram for ![]() deg. (---leg 1 and ---leg 2)
deg. (---leg 1 and ---leg 2)
![]()
![]() (a) (b)
(a) (b)
Figure 10. 8-periodic limit cycles: (a) a diagram of impact time vs step numbers; (b) phase space diagram for ![]() deg. (---leg 1 and ---leg 2)
deg. (---leg 1 and ---leg 2)
![]()
![]() (a) (b)
(a) (b)
Figure 11. Chaotic limit cycles: (a) a diagram of impact time vs step numbers; (b) phase space diagram for ![]() deg. (---leg 1 and ---leg 2)
deg. (---leg 1 and ---leg 2)
Acknowledgements
This research is partially funded by DST-FIST2014 file number: MS1-097.