Assessing the Influence of Quiescence Eggs on the Dynamics of Mosquito Aedes aegypti ()
1. Introduction
The population dynamics of mosquitoes Aedes aegypti is clearly dependent on abiotic factors, with serious implications for dengue transmission. By using estimated entomological parameters dependent on temperature, including the dependency of these parameters on rainfall, the seasonally varying population size of mosquito A. aegypti was evaluated by a mathematical model [1] . However, eggs are known to be the most resistant stages during development, allowing a long survival of the mosquitoes under unfavorable climatic conditions, such as lower temperatures and dry seasons [2] [3] .
The eggs of the mosquito A. aegypti possess the ability to undergo an extended quiescence hosting a fully developed 1st instar larvae within the chorion, and this life history traitpharate larvae can withstand months of quiescence inside the egg where they depend on stored maternal reserves. Therefore, the duration of quiescence and extent of nutritional depletion may affect the physiology and survival of larvae that hatch in a suboptimal habitat [4] .
Silva and Silva [5] carried out laboratorial experiments in order to determine the influence of the quiescence eggs on the life cycle of A. aegypti. Their experiments allow classifying the quiescence eggs in roughly four categories according to their ability to hatch larvae (see Section 4 for details). In this paper, these four stages of quiescence eggs are included in the modelling of the dynamics of A. aegypti [6] , aiming to assess their influences on the size of mosquito population. This assessment is performed by determining the improvement of the fitness of mosquito population due to the quiescence eggs.
The paper is structured as follows. In Section 2, a model for A. aegypti population is formulated encompassing quiescence eggs, and in Section 3 the model is analyzed, determining the equilibrium points, and performing the stability analysis of these points. Section 4 presents discussion, and conclusion is given in Section 5.
2. Model Formulation
Embryonic development of the eggs of the mosquito A. aegypti is completed approximately within 3 days after oviposition, and a fully developed 1st instar larva resides within the chorion of the egg in a dormant state referred to as quiescence. Pharate 1st instar quiescent larvae will hatch out immediately upon exposure to the appropriate stimulus; in this way quiescence differs from diapause, which is a hormonally controlled and pre-programmed state of developmental arrest in which the larvae are refractory to hatching stimuli for an extended period of time. As a result of this life history trait, A. aegypti produce eggs that, in addition to being desiccation resistant, can withstand months of dormancy depending on stored maternal reserves [4] . The influence of these quiescence eggs on the population dynamics of A. aegypti mosquitoes is assessed by mathematical modelling.
The life cycle of A. aegypti encompasses an aquatic phase (egg, larva and pupa) followed by winged (adult) form. In Yang et al. [6] , a mathematical model considering the compartments of aquatic phase (encompassing larvae and pupae) and adult mosquitoes was analyzed. However, the model developed here takes into account the compartment of eggs. Hence, the dynamics of mosquito population encompasses three phases in the life cycle of A. aegypti: eggs, aquatic phase and adult mosquitoes. The model considers only female mosquitoes , and two different stages of eggs (the quiescence eggs
, and two different stages of eggs (the quiescence eggs 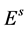 and hatchable eggs E), distributed in four compartments according to the period of time they are quiescence (
and hatchable eggs E), distributed in four compartments according to the period of time they are quiescence ( and
and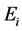 , for
, for ), while aquatic phase comprises larva and pupa stages
), while aquatic phase comprises larva and pupa stages . The passage from
. The passage from 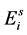 to
to  is dictated by external stimuli (such as temperature, humidity, nutrients, etc.) and is irreversible. See the flow chart in Figure 1.
is dictated by external stimuli (such as temperature, humidity, nutrients, etc.) and is irreversible. See the flow chart in Figure 1.
In the modelling, it is assumed that all eggs laid by mosquitoes enter in the first quiescence stage, which number at time t is designated as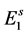 . The rate at which eggs are produced is given by
. The rate at which eggs are produced is given by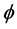 , the oviposition rate, and among them a fraction
, the oviposition rate, and among them a fraction 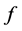 will originate female mosquitoes. These eggs are transferred to second quiescence stage
will originate female mosquitoes. These eggs are transferred to second quiescence stage 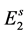 after a period of time
after a period of time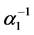 , where
, where 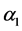 is the transition rate from
is the transition rate from 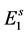 to
to ; or, they enter to hatchable state
; or, they enter to hatchable state ![]() at rate
at rate![]() . The eggs in the hatchable state
. The eggs in the hatchable state ![]() hatch as larvae at eclosion rate
hatch as larvae at eclosion rate![]() , and enter to the aquatic phase A. Another route is the death (inviabilization) of hatchable eggs at mortality rate
, and enter to the aquatic phase A. Another route is the death (inviabilization) of hatchable eggs at mortality rate![]() , but
, but
![]()
Figure 1. The flow chart of mosquito’s life cycle in- cluding quiescence eggs.
it is assumed that the eggs in quiescence stage ![]() are not under mortality. The number of aquatic forms is constrained by breeding sites and nutrients, which is designated by
are not under mortality. The number of aquatic forms is constrained by breeding sites and nutrients, which is designated by![]() , the carrying capacity. In aquatic phase, larvae develop to pupae, and emerge as adult
, the carrying capacity. In aquatic phase, larvae develop to pupae, and emerge as adult ![]() at rate
at rate![]() , or they (in larval and pupal phases) die at mortality rate
, or they (in larval and pupal phases) die at mortality rate![]() . Finally, the adult mosquitoes die at mortality rate
. Finally, the adult mosquitoes die at mortality rate![]() . Notice that the inverse of the mortality rate
. Notice that the inverse of the mortality rate ![]() is the average period of surviving in the state
is the average period of surviving in the state![]() , where
, where ![]() stands for all compartments except quiescence stages; and the mating between male and female mosquitoes is not considered in the modelling [7] .
stands for all compartments except quiescence stages; and the mating between male and female mosquitoes is not considered in the modelling [7] .
The above descriptions are also valid for the quiescence eggs ![]() and hatchable eggs
and hatchable eggs![]() , for
, for![]() . The definitions of the parameters are the same described above, changing the subscript for 2, 3 or 4. Being the fourth stage of eggs the last,
. The definitions of the parameters are the same described above, changing the subscript for 2, 3 or 4. Being the fourth stage of eggs the last,![]() . The entomological parameters
. The entomological parameters ![]()
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() and
and ![]() are strongly dependent on temperature (consequently on time t), but
are strongly dependent on temperature (consequently on time t), but ![]() do not.
do not.
Based on the foregoing descriptions of model parameters and variables, the dynamics of mosquito population encompassing quiescence eggs is described by the system of differential Equations
![]() (1)
(1)
This system of equations is analyzed in the steady state. A simplified version of this modelling is given in Appendix.
3. Analysis of the Model
The system of Equations (1) is dealt with determining the equilibrium points, and assessing the stability of these points.
3.1. Equilibrium Points
Before determining the equilibrium points, let the following parameters be defined. The quiescence eggs at stage i can go to next quiescence stage ![]() or to hatchable state i, with probabilities of transition from quiescence stage i to stage
or to hatchable state i, with probabilities of transition from quiescence stage i to stage ![]()
![]() and to hatchable stage i
and to hatchable stage i![]() being given by
being given by
![]() (2)
(2)
for![]() , with
, with![]() . Notice that
. Notice that ![]() and
and![]() , due to
, due to![]() . The average periods of time that eggs stay at quiescence
. The average periods of time that eggs stay at quiescence ![]() and hatchable
and hatchable ![]() stages i are
stages i are
![]() (3)
(3)
for![]() . Finally, the probability of eggs surviving the hatchable stage i and hatch as larvae
. Finally, the probability of eggs surviving the hatchable stage i and hatch as larvae![]() , and the probability of aquatic forms (larvae and pupae) surviving the aquatic phase and emerging as adult mosquitoes
, and the probability of aquatic forms (larvae and pupae) surviving the aquatic phase and emerging as adult mosquitoes ![]() are
are
![]() (4)
(4)
for![]() .
.
There are two equilibrium points. The first equilibrium is the absence of mosquito population, designated by![]() , given by
, given by
![]()
which is referred to the trivial equilibrium point.
The second equilibrium is the mosquito population being well established in a region (or community), the non-trivial equilibrium![]() , given by
, given by
![]()
The coordinates of the non-trivial equilibrium are written in terms of the previously defined parameters, which are
![]()
and the number of adult mosquitoes ![]() is
is
![]()
where ![]() is the basic offspring number defined by
is the basic offspring number defined by
![]() (5)
(5)
with ![]() being given by
being given by
![]() (6)
(6)
which is the overall production of larvae by all compartments of eggs. Clearly, the non-trivial equilibrium point is biologically feasible if![]() .
.
Let ![]() be interpreted biologically. Suppose that a fertilized female mosquito is introduced in a region completely free of mosquitoes. The term
be interpreted biologically. Suppose that a fertilized female mosquito is introduced in a region completely free of mosquitoes. The term ![]() is the average number of (female) eggs produced by this mosquito. These eggs are spread out among the four compartment with different probabilities of hatching according to the period of time they are stored as quiescence stage. Average number of eggs that survive these compartments and hatch as larvae is given by
is the average number of (female) eggs produced by this mosquito. These eggs are spread out among the four compartment with different probabilities of hatching according to the period of time they are stored as quiescence stage. Average number of eggs that survive these compartments and hatch as larvae is given by![]() , which must survive also the aquatic phase and emerge as adult (female) mosquitoes, with probability
, which must survive also the aquatic phase and emerge as adult (female) mosquitoes, with probability![]() . Hence,
. Hence, ![]() is the average number of offsprings originated by a single female mosquito introduced in a region free of mosquitoes.
is the average number of offsprings originated by a single female mosquito introduced in a region free of mosquitoes.
The overall production of eggs ![]() also deserves interpretation. All eggs enter into the class
also deserves interpretation. All eggs enter into the class![]() . Among these eggs, a fraction
. Among these eggs, a fraction ![]() enters to the hatchable state
enters to the hatchable state ![]() and, when surviving this stage with probability
and, when surviving this stage with probability![]() , become larvae, resulting in
, become larvae, resulting in ![]() aquatic forms produced by the eggs following the route
aquatic forms produced by the eggs following the route ![]() and
and![]() . But, the complementary fraction
. But, the complementary fraction ![]() is transferred to quiescence stage
is transferred to quiescence stage![]() . Among these eggs,
. Among these eggs, ![]() enters to the hatchable state
enters to the hatchable state ![]() and complementary fraction
and complementary fraction ![]() is transferred to quiescence stage
is transferred to quiescence stage![]() . Following previously definition,
. Following previously definition, ![]() is the average number of larvae produced by eggs that remained quiescence without entering in the first hatchable state
is the average number of larvae produced by eggs that remained quiescence without entering in the first hatchable state![]() , but entered in the second hatchable state
, but entered in the second hatchable state ![]() and survived this state
and survived this state![]() . This is the path of eggs following the route
. This is the path of eggs following the route![]() ,
, ![]() and
and ![]() before hatching. The third (
before hatching. The third (![]() , following the route
, following the route![]() ,
, ![]() ,
, ![]() and
and ![]() before hatching) and fourth (
before hatching) and fourth (![]() , following the route
, following the route![]() ,
, ![]() ,
, ![]() ,
, ![]() and
and ![]() before hatching) terms follow similar interpretation. Hence
before hatching) terms follow similar interpretation. Hence ![]() is the overall production of aquatic forms by the four quiescence and hatchable compartments.
is the overall production of aquatic forms by the four quiescence and hatchable compartments.
3.2. Stability Analysis of the Equilibrium Points
The stability analysis of the equilibrium points ![]() and
and ![]() are assessed by the application of Routh-Hurwitz criteria to the characteristic Equation corresponding to the Jacobian matrix of Equation (1).
are assessed by the application of Routh-Hurwitz criteria to the characteristic Equation corresponding to the Jacobian matrix of Equation (1).
The Jacobian matrix evaluated at the equilibrium point![]() , named
, named![]() , results in
, results in
![]()
where the ![]() matrices
matrices![]() , with
, with![]() , are
, are
![]()
with![]() ,
, ![]() ,
, ![]() ,
, ![]() and
and![]() ,
,
![]()
![]()
with![]() , and
, and
![]()
with![]() ,
, ![]() and
and![]() . The local stability of the equilibrium points is assessed by the eigenvalues of the characteristic Equation
. The local stability of the equilibrium points is assessed by the eigenvalues of the characteristic Equation ![]() [8] , or
[8] , or
![]()
which can be written as
![]()
a polynomial of ![]() degree.
degree.
The independent term of the characteristic Equation, designated by L0, which is given by![]() , is written as
, is written as
![]()
where ![]() is given by
is given by
![]()
For the trivial equilibrium![]() ,
, ![]() , and for the non-trivial equilibrium
, and for the non-trivial equilibrium![]() ,
, ![]() , resulting in
, resulting in
![]()
Hence, according to Leite et al. [9] , the trivial equilibrium point ![]() is locally asymptotically stable for
is locally asymptotically stable for![]() , and the non-trivial equilibrium
, and the non-trivial equilibrium ![]() is stable for
is stable for![]() .
.
4. Discussion
The results obtained in previous section are dealt with to assess the influence of the quiescence eggs in the size of A. aegypti population. First, the study is done qualitatively, and, then, the results are confronted with experimental data.
4.1. Assessing Qualitatively the Effects of Quiescence
The basic offspring number![]() , given by Equation (5), is the average number of offsprings generated by a single fertilized mosquito considering four different stages of quiescence. Let this threshold parameter be compared with
, given by Equation (5), is the average number of offsprings generated by a single fertilized mosquito considering four different stages of quiescence. Let this threshold parameter be compared with![]() , the basic offspring number without quiescence stages, which is given by
, the basic offspring number without quiescence stages, which is given by
![]() (7)
(7)
Notice that this is obtained by letting ![]() (consequently,
(consequently,![]() ) in Equation (5). The difference between
) in Equation (5). The difference between ![]() and
and ![]() is taken as a measure of fitness of mosquito population by adopting the strategy of quiescence: If
is taken as a measure of fitness of mosquito population by adopting the strategy of quiescence: If![]() , then there is a gain in the fitness promoted by quiescence eggs; if not, there is loss of fitness.
, then there is a gain in the fitness promoted by quiescence eggs; if not, there is loss of fitness.
Let first be defined the productivity of each hatchable stage![]() , with
, with![]() . Suppose an initial number of hatchable eggs
. Suppose an initial number of hatchable eggs ![]() is in the stage i, and there is no influx. Hence, the number of eggs at time
is in the stage i, and there is no influx. Hence, the number of eggs at time ![]() is given by
is given by
![]() . The number of eggs hatching to larvae between t and
. The number of eggs hatching to larvae between t and ![]() is given by
is given by![]() , as well as the
, as well as the
number of died eggs is![]() . The quocient between the total numbers of production of larvae and died eggs
. The quocient between the total numbers of production of larvae and died eggs ![]() is
is
![]() (8)
(8)
![]() , which is called the productivity index of hatchable state
, which is called the productivity index of hatchable state![]() . This index does not reflect the velocity of transitions from hatchable state to aquatic phase, but only the ratio between eclosion and mortality of eggs.
. This index does not reflect the velocity of transitions from hatchable state to aquatic phase, but only the ratio between eclosion and mortality of eggs.
The difference between ![]() and
and![]() , Equations (5) and (7), is
, Equations (5) and (7), is
![]()
where ![]() is given by
is given by
![]()
and ![]() is given by
is given by
![]()
where
![]() (9)
(9)
with ![]() being the solution of
being the solution of![]() . Hence, the signal of
. Hence, the signal of ![]() will be determined by the signal of
will be determined by the signal of![]() .
.
Notice that the parameters![]() ,
, ![]() and
and ![]() do not appear in
do not appear in![]() , showing that these parameters do not affect in the change of fitness of the mosquito population. (These parameters affects in the magnitude of the difference
, showing that these parameters do not affect in the change of fitness of the mosquito population. (These parameters affects in the magnitude of the difference![]() .) The parameters
.) The parameters![]() ,
, ![]() and
and ![]() can be increased by increasing the parameters
can be increased by increasing the parameters ![]() and
and![]() , and
, and
![]() (10)
(10)
There are four hatchable states![]() , originating from quiescence stages of eggs
, originating from quiescence stages of eggs![]() , with different productivity of larvae
, with different productivity of larvae![]() . The gain in the fitness promoted by quiescence eggs is studied taking into account the productivity index
. The gain in the fitness promoted by quiescence eggs is studied taking into account the productivity index![]() . When
. When ![]() changes the productivity with any other state
changes the productivity with any other state![]() ,
, ![]() , it is assumed that
, it is assumed that ![]() remains producing more larvae than other two stages.
remains producing more larvae than other two stages.
A.![]() ,
, ![]() and
and![]() —The first hatchable state
—The first hatchable state ![]() is the most proficuous in larvae production.
is the most proficuous in larvae production.
In this case, ![]() and
and![]() , resulting in
, resulting in![]() . Hence
. Hence![]() , and the quiescence eggs decrease the fitness of mosquito population.
, and the quiescence eggs decrease the fitness of mosquito population.
B.![]() ,
, ![]() and
and![]() —The second hatchable state
—The second hatchable state ![]() is the most proficuous in larvae production.
is the most proficuous in larvae production.
In this case, ![]() and
and![]() , resulting in two possibilities:
, resulting in two possibilities:
B.1.![]() —the third hatchable state
—the third hatchable state ![]() is more proficuous than
is more proficuous than![]() .
.
In this case, ![]() , according to Equation (10), and the threshold of
, according to Equation (10), and the threshold of ![]() is defined by
is defined by![]() . In this case,
. In this case,
![]() (11)
(11)
Hence, the quiescence eggs increase the fitness of mosquito population ![]() in two situations: 1) when the influx is at lower level
in two situations: 1) when the influx is at lower level ![]() in quiescence stage
in quiescence stage![]() , and 2) the influx is at moderate level
, and 2) the influx is at moderate level ![]() and the outflux is lower
and the outflux is lower ![]() in quiescence stage
in quiescence stage![]() .
.
B.2.![]() —The fourth hatchable state
—The fourth hatchable state ![]() is more proficuous than
is more proficuous than![]() .
.
In this case, ![]() , according to Equation (10), and the threshold of
, according to Equation (10), and the threshold of ![]() is defined by
is defined by![]() . In this case,
. In this case,
![]() (12)
(12)
Hence, the quiescence eggs increase the fitness of mosquito population ![]() in two situations: 1) when the influx is at lower level
in two situations: 1) when the influx is at lower level ![]() in quiescence stage
in quiescence stage![]() , and 2) the influx is at moderate level
, and 2) the influx is at moderate level ![]() and the outflux is higher
and the outflux is higher ![]() in quiescence stage
in quiescence stage![]() .
.
C.![]() ,
, ![]() and
and![]() —The third hatchable state
—The third hatchable state ![]() is the most proficuous in larvae pro- duction.
is the most proficuous in larvae pro- duction.
In this case, ![]() and
and![]() , and the threshold of
, and the threshold of ![]() is given by
is given by![]() . In this case,
. In this case,
![]() (13)
(13)
Hence, the quiescence eggs increase the fitness of mosquito population ![]() when the influx is at higher level
when the influx is at higher level ![]() but the outflux is lower
but the outflux is lower ![]() in quiescence stage
in quiescence stage![]() .
.
D.![]() ,
, ![]() and
and![]() —The fourth and last hatchable state
—The fourth and last hatchable state ![]() is the most proficuous in larvae production.
is the most proficuous in larvae production.
In this case, ![]() and
and![]() , and the threshold of
, and the threshold of ![]() is given by
is given by![]() . In this case,
. In this case,
![]() (14)
(14)
Hence, the quiescence eggs increase the fitness of mosquito population ![]() when both influx
when both influx ![]() and outflux
and outflux ![]() in quiescence stage
in quiescence stage ![]() are at higher levels.
are at higher levels.
Summarizing, the quiescence eggs increase the fitness of mosquito population if one of hatchable stages from![]() ,
, ![]() and
and ![]() is more proficuous (higher productivity index p) than E1. Besides the productivity indexes
is more proficuous (higher productivity index p) than E1. Besides the productivity indexes![]() , the parameters
, the parameters ![]() and
and![]() , which are the influx and outflux rates in the quiescence stage
, which are the influx and outflux rates in the quiescence stage![]() , play important role in the fitness. The quiescence eggs increase the fitness of mosquito population if: a) the second hatchable state
, play important role in the fitness. The quiescence eggs increase the fitness of mosquito population if: a) the second hatchable state ![]() is the most proficuous in larvae production, and
is the most proficuous in larvae production, and ![]() assumes lower values and
assumes lower values and ![]() assumes lower or higher values according to the relative productivities of
assumes lower or higher values according to the relative productivities of ![]() and
and![]() , Equations (11) and (12); b) the third hatchable state
, Equations (11) and (12); b) the third hatchable state ![]() is the most proficuous in larvae production, and
is the most proficuous in larvae production, and ![]() assumes higher values, while
assumes higher values, while ![]() assumes lower values, Equation (13); and c) the fourth hatchable state
assumes lower values, Equation (13); and c) the fourth hatchable state ![]() is the most proficuous in larvae production, and
is the most proficuous in larvae production, and ![]() and
and ![]() assume higher values, Equation (14).
assume higher values, Equation (14).
The transition parameters![]() , with
, with![]() , depend strongly on the abiotic factors. In contrast,
, depend strongly on the abiotic factors. In contrast, ![]() , with
, with![]() , are fixed. However, the corresponding thresholds of
, are fixed. However, the corresponding thresholds of ![]() and
and ![]() are allowed to vary by varying
are allowed to vary by varying ![]() and
and ![]() according to Equation (9). For this reason the threshold parameters
according to Equation (9). For this reason the threshold parameters ![]() (which can be
(which can be ![]() or
or![]() ) and
) and ![]() are varied in order to
are varied in order to ![]() and
and ![]() be situated at higher or lower values with respect to corresponding thresholds. Hence, the thresholds of
be situated at higher or lower values with respect to corresponding thresholds. Hence, the thresholds of ![]() and
and ![]() are obtained for fixed values of
are obtained for fixed values of ![]() and
and![]() , that is, letting
, that is, letting ![]() and
and ![]() in Equation (9). The resulting thresholds of
in Equation (9). The resulting thresholds of ![]() and
and ![]() are
are
![]() (15)
(15)
Hence, depending on the productivity index![]() , the parameters
, the parameters ![]() and
and ![]() can be settle below or above the thresholds
can be settle below or above the thresholds ![]() which can be
which can be ![]() or
or![]() ) and
) and![]() , in order to the thresholds
, in order to the thresholds ![]() and
and ![]() be situated above or below the values of
be situated above or below the values of ![]() and
and![]() , respectively. If one of the conditions given by Equations (11), (12), (13) and (14) is satisfied, then the quiescence eggs increase the fitness of A. aegypti population.
, respectively. If one of the conditions given by Equations (11), (12), (13) and (14) is satisfied, then the quiescence eggs increase the fitness of A. aegypti population.
4.2. Comparing with Experimental Data
The theoretical results obtained in foregoing section are compared with the results of the experiments carried out by Silva and Silva [5] , which are reproduced in Table 1. The laboratory experiments to determine the influence of different periods of quiescence on eclosion of eggs to larvae were performed in a biological chamber kept at 28˚C, 80% relative humidity and 12 hours of photophase.
![]()
Table 1. Reproduction of the results obtained by silva and silva [1] .
Based on Table 1, Table 2 presents the estimation of the per-capita eclosion and mortality rates according to ![]() and
and![]() , where
, where![]() , N and
, N and ![]() are, respectively, the number of eggs, total eclosion rate and percentage of eclosion (columns
are, respectively, the number of eggs, total eclosion rate and percentage of eclosion (columns![]() ,
, ![]() and
and ![]() of Table 1).
of Table 1).
Observing the last column of Table 1, the 11 experiments can be clustered as follows: Experiment number 1 as quiescence stage 1, experiment numbers 2 to 4 as quiescence stage 2, experiment number 5 as quiescence stage 3, and, finally, experiment numbers 7 to 11 as quiescence stage 4. In Table 3, the mean eclosion ![]() and mortality
and mortality ![]() rates, the productivity index
rates, the productivity index![]() , transition rate
, transition rate ![]() and hatchable rate
and hatchable rate ![]() are presented. With respect to transition rate, it is assumed that the average periods of time (days) in quiescence stages are
are presented. With respect to transition rate, it is assumed that the average periods of time (days) in quiescence stages are![]() ,
, ![]() and
and ![]() (notice that
(notice that![]() , since this is the last stage). With respect to hatchable rate, it is set arbitrarily as
, since this is the last stage). With respect to hatchable rate, it is set arbitrarily as ![]() (see appendix). Notice that the third quiescence stage is the most proficuous in larvae production
(see appendix). Notice that the third quiescence stage is the most proficuous in larvae production![]() , which was also observed by other authors [10] [11] , and it corresponds to the case C shown in preceding section.
, which was also observed by other authors [10] [11] , and it corresponds to the case C shown in preceding section.
The estimated eclosion ![]() and mortality
and mortality ![]() rates of aquatic phase, the mortality rate of adult female mosquitoes
rates of aquatic phase, the mortality rate of adult female mosquitoes ![]() and the oviposition rate per female
and the oviposition rate per female ![]() are given in Table 4 [6] . These rates are given for two different temperatures (16˚C and 28˚C), in order to mimic favorable (summer or wet) and unfavorable (winter or dry) seasons. To the favorable seasons, the temperature of 28˚C was chosen due to the laboratorial experiments in [5] .
are given in Table 4 [6] . These rates are given for two different temperatures (16˚C and 28˚C), in order to mimic favorable (summer or wet) and unfavorable (winter or dry) seasons. To the favorable seasons, the temperature of 28˚C was chosen due to the laboratorial experiments in [5] .
![]()
Table 2. Calculation of the per-capita eclosion and mortality rates.
![]()
Table 3. Estimation of the parameters σi, μi, calculation of the productivity indexes![]() , αi and εi, for i = 1, ···, 4.
, αi and εi, for i = 1, ···, 4.
![]()
Table 4. The estimated values of the parameters σa, μa, μf and f for 16 and 28 degree Celsius (˚C) [2] .
Table 5 presents the values of the critical parameters and the basic offspring number. Using values of parameters given in Table 3 and Table 4, the threshold values (![]() ) of
) of ![]() and
and ![]() are
are ![]()
and ![]() (second column), and the corresponding basic offspring number is
(second column), and the corresponding basic offspring number is![]() . Since
. Since![]() , from the case C described above,
, from the case C described above, ![]() for all
for all![]() , resulting in
, resulting in![]() , where
, where ![]() was calculated using Equation (7). Hence, using
was calculated using Equation (7). Hence, using ![]() and
and ![]() (Table 3), the quiescence eggs decrease the fitness of mosquito population.
(Table 3), the quiescence eggs decrease the fitness of mosquito population.
Table 5 additionally shows that the threshold values (![]() ) of
) of ![]() and
and ![]() are
are ![]() and
and![]() . Remembering that the values of
. Remembering that the values of ![]() and
and ![]() are fixed, while
are fixed, while ![]() and
and ![]() are allowed to vary, the thresholds
are allowed to vary, the thresholds ![]() and
and ![]() changed appropriately in order to satisfy
changed appropriately in order to satisfy![]() , which is true if the conditions
, which is true if the conditions ![]() and
and ![]() are verified, according to Equation (13). From the case C described above,
are verified, according to Equation (13). From the case C described above, ![]() (the quiescence eggs increase the fitness of mosquito population) is possible when
(the quiescence eggs increase the fitness of mosquito population) is possible when ![]() and
and![]() . Since
. Since ![]() and
and ![]() are arbitrary values, the first condition
are arbitrary values, the first condition ![]() is satisfied for all
is satisfied for all ![]() that satisfy
that satisfy![]() . For this reason, only the value of
. For this reason, only the value of ![]() is changed in Table 3, or
is changed in Table 3, or ![]()
![]() , in order to decrease
, in order to decrease ![]() and to satisfy the first condition. In this case, the new threshold (
and to satisfy the first condition. In this case, the new threshold (![]() ) is
) is ![]() (other critical values are given in the third column of Table 5), and the corresponding basic offspring number is
(other critical values are given in the third column of Table 5), and the corresponding basic offspring number is![]() , smaller than the previous case. Similarly, the second condition is satisfied if
, smaller than the previous case. Similarly, the second condition is satisfied if![]() , which is the reason to choose
, which is the reason to choose ![]()
![]() . This additional change alters only
. This additional change alters only ![]() (fourth column of Table 5), but the corresponding basic offspring number is
(fourth column of Table 5), but the corresponding basic offspring number is![]() , slightly higher than
, slightly higher than![]() . The partial contributions of all eggs compartments to the overall
. The partial contributions of all eggs compartments to the overall ![]() are given in Table 6.
are given in Table 6.
The contribution of the first stage of quiescence eggs in all cases, as shown in Table 6, does not change due to change occurring in ![]() and
and![]() . With the new values
. With the new values ![]() and
and ![]() (
(![]() ), the contribution of the third quiescence eggs compartment increased in almost 10 times, and became the highest contributor, displacing the first stage. The basic offspring number corresponding to the simplified model is given by the first row of Table 6 (see Appendix).
), the contribution of the third quiescence eggs compartment increased in almost 10 times, and became the highest contributor, displacing the first stage. The basic offspring number corresponding to the simplified model is given by the first row of Table 6 (see Appendix).
Summarizing, assuming that![]() ,
, ![]() and
and ![]() do not change, when the values of
do not change, when the values of ![]() and
and ![]() (
(![]() ) in Table 3 (0.0277 and 0.0181) are changed to 0.001 and 0.5, respectively, then the quiescence eggs increase the fitness of mosquito population. Notice that the values of
) in Table 3 (0.0277 and 0.0181) are changed to 0.001 and 0.5, respectively, then the quiescence eggs increase the fitness of mosquito population. Notice that the values of ![]() and
and ![]() do not matter in this issue.
do not matter in this issue.
Up to now the model was discussed considering constant values for the model parameters. But, the effect of
![]()
Table 6. The basic reproduction number Q0 calculated using the values given in Table 3 and Table 4. The basic repro- duction number corresponding to a unique eggs compartment is ![]() = 81.158.
= 81.158.
quiescence eggs in the size of mosquito population becomes important in tropical (wet and dry seasons) and temperate (rigorous winter seasons) regions.
The experiments carried out by Silva and Silva [5] showed that eggs of A. aegypti presented more productivity index after being stored for 4 months. This period encompasses the unfavorable seasons (dry or/and cold). After this period, in the beginning of favorable seasons, mosquito population can be settled quickly at higher infestation levels. Table 7 shows the partial contributions of quiescence eggs to overall basic offspring number. Two seasons (summer, 28˚C, and winter, 16˚C) and two extreme abiotic conditions, the favorable (high) and unfavorable (low), according to equal ![]() hatchable rates
hatchable rates ![]() and
and ![]() (
(![]() ), respectively. The values of eclosion and mortality rates
), respectively. The values of eclosion and mortality rates ![]() and
and ![]() are maintained fixed in all seasons, because the experiments in [5] were carried out for a unique temperature (28˚C).
are maintained fixed in all seasons, because the experiments in [5] were carried out for a unique temperature (28˚C).
In a favorable abiotic conditions (high![]() ), the partial contribution of first stage of quiescence eggs is almost the overall offspring number. However, in hostile abiotic conditions (low
), the partial contribution of first stage of quiescence eggs is almost the overall offspring number. However, in hostile abiotic conditions (low![]() ), the quiescence stages 2, 3 and 4, in this order, contribute more than first quiescence stage to overall offspring number. This behavior has important influence in seasonality of abiotic conditions. For instance, in the end of favorable seasons, more eggs are transferred to quiescence stages than to hatchable states, due to decreasing in the hatchable rates
), the quiescence stages 2, 3 and 4, in this order, contribute more than first quiescence stage to overall offspring number. This behavior has important influence in seasonality of abiotic conditions. For instance, in the end of favorable seasons, more eggs are transferred to quiescence stages than to hatchable states, due to decreasing in the hatchable rates ![]() (for instance, the row labelled “summer (low)” of Table 7,
(for instance, the row labelled “summer (low)” of Table 7,![]() ). After the passage of unfavorable season (“winter (low)” of Table 7,
). After the passage of unfavorable season (“winter (low)” of Table 7,![]() ), eggs are allowed to hatch in the beginning of next favorable season (“winter (high)” of Table 7,
), eggs are allowed to hatch in the beginning of next favorable season (“winter (high)” of Table 7,![]() ), remembering that these eggs have been stored for around 4 months. However, these quiescence eggs are highly proficuous in originating larvae (high productivity index of hatching). During this transition of seasons, these quiescence eggs contribute mainly to recolonize the region quickly. Sinceafter, the population of mosquitoes is maintained at the infestation level due to the increasing of hatchable rates
), remembering that these eggs have been stored for around 4 months. However, these quiescence eggs are highly proficuous in originating larvae (high productivity index of hatching). During this transition of seasons, these quiescence eggs contribute mainly to recolonize the region quickly. Sinceafter, the population of mosquitoes is maintained at the infestation level due to the increasing of hatchable rates ![]() to the previous values (“summer (high)” of Table 7,
to the previous values (“summer (high)” of Table 7,![]() ). Notice that the variation of
). Notice that the variation of ![]() times in
times in ![]() resulted only in a variation of 10 times in
resulted only in a variation of 10 times in![]() .
.
5. Conclusions
A mathematical model encompassing four quiescence stages was analyzed. From the model, it was concluded that under certain conditions, the quiescence eggs can improve the fitness of A. aegypti population.
The capacity of the A. aegypti eggs being stored during hostile abiotic factors and, then, hatching to larvae in favorable season with increased fitness, is essential to sustain A. aegypti population to face seasonality. When the quiescence eggs having approximately 120 days are allowed to hatch, these eggs presented the most producible capacity to originate larvae [5] . This period of 4 months corresponds to approximately the worst abiotic conditions to A. aegypti to survive. Hence, the quiescence of eggs of 4 months joined to the higher capacity of hatching seems to be an important strategy to A. aegypti population to persist in seasonally varying environment.
Another aspect is regarded to dengue transmission, due to the possibility of the eggs infected with dengue virus sustaining dengue epidemics [12] . For this reason, it is important to analyze dengue transmission modelling taking into account the infected and non-infected quiescence eggs. One of the possible applications of this kind of modelling is the assessment of biological control by intracellular bacterium Wolbachia [13] .
Quantitative analyses, such as the dynamical trajectories, are left to further work. For instance, the dynamical trajectories of the system of Equations (1) are obtained numerically considering the initial conditions, at t = 0, given by
![]()
Table 7. The basic offspring number Q0 calculated using the values given in Table 3 and Table 4, varying only the transition rates εi for two seasons: Summer (28˚C) and winter (16˚C). Two values are used for i = 1, ···, 4 (days−1): εi = 5.0 (high) and εi = 0.001 (low). The basic reproduction number corresponding to a unique eggs compartment is ![]() = 5.327 for winter season (for summer, the values is that provided in Table 6).
= 5.327 for winter season (for summer, the values is that provided in Table 6).
![]()
which corresponds to the introduction of one mosquito in a previously uninfested region. In other words, the equilibrium point before the introduction of infectious case is given by![]() . Depending on the value of the basic offspring number, the mosquito population goes to extinction (
. Depending on the value of the basic offspring number, the mosquito population goes to extinction (![]() , when
, when![]() ), or colonizes successfully (
), or colonizes successfully (![]() , when
, when![]() ).
).
Funding
Projeto temático FAPESP grant 09/15098-0.
Appendix
Simplified Model
The model described by system of Equations (1) can be simplified joining the quiescence and hatchable stages. For instance, calling![]() , then (for
, then (for![]() ,
,![]() )
)
![]()
is approximated as
![]()
for![]() . This simplification allows the system to eliminate four equations. The simplified system is
. This simplification allows the system to eliminate four equations. The simplified system is
![]()
where the prime was dropped out.
Defining the average period of time that eggs stay at stage i ![]() as
as
![]()
with![]() , and the probabilities of eggs at stage i going to next stage i + 1
, and the probabilities of eggs at stage i going to next stage i + 1 ![]() or to hatch at stage i
or to hatch at stage i![]() , and probability of surviving aquatic phase
, and probability of surviving aquatic phase ![]() as
as
![]()
for![]() , two equilibrium points are given.
, two equilibrium points are given.
The first equilibrium is the absence of mosquito population, the trivial equilibrium![]() , given by
, given by
![]()
The non-trivial equilibrium ![]() is given by
is given by
![]()
where the coordinates written in terms of the previously defined parameters are
![]()
and the number of adult mosquitoes ![]() is
is
![]()
The basic offspring number ![]() is defined by
is defined by
![]() (16)
(16)
with ![]() being given by
being given by
![]()
which is the overall production of larvae by all compartments of eggs. Clearly, the non-trivial equilibrium point is biologically feasible if![]() .
.
Letting![]() , the basic offspring number
, the basic offspring number ![]() without quiescence stages is equal to Equation (7), which can be obtained by letting
without quiescence stages is equal to Equation (7), which can be obtained by letting ![]() in Equation (16). The difference between
in Equation (16). The difference between ![]() and
and ![]() is
is
![]()
where ![]() is given by
is given by
![]()
and ![]() is given by
is given by
![]()
where
![]()
with
![]()
Notice that ![]() and
and ![]() are the critical values given by Equation (9) dropping out the factor
are the critical values given by Equation (9) dropping out the factor![]() , while for
, while for![]() , the absent factor is
, the absent factor is![]() . For this reason, in Table 3, the values for
. For this reason, in Table 3, the values for![]() ,
, ![]() , were set
, were set![]() . Using values given in Table 3 and Table 4, from the second column of Table 5, the inequality
. Using values given in Table 3 and Table 4, from the second column of Table 5, the inequality ![]() is always true. Remember that
is always true. Remember that ![]() and
and![]() .
.
Conversely to the general model, the simplified version of the model does not allow the change in the critical values![]() ,
, ![]() and
and ![]() in order to obtain situations where
in order to obtain situations where ![]() (see Equations (11), (12), (13) and (14), corresponding to cases B, C and D in main text).
(see Equations (11), (12), (13) and (14), corresponding to cases B, C and D in main text).
NOTES
*Corresponding author.