Empirical Likelihood Diagnosis of Modal Linear Regression Models ()
1. Introduction
The mode of a distribution is regarded as an important feature of data. Several authors have made efforts to identify the modes of population distributions for low-dimensional data. See, for example, Muller and Sawitzki [1] ; Scott [2] ; Friedman and Fisher [3] ; Chaudhuri and Marron [4] ; Fisher and Marron [5] ; Davies and Kovac [6] Hall, Minnotte and Zhang [7] ; Ray and Lindsay [8] ; Yao and Lindsay [9] . In high-dimensional data, it is common to impose some model structure assumptions such as assumption on conditional distributions. Thus, it is of great interest to study the mode hunting for conditional distributions.
Given a random sample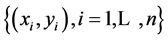
, where 
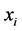is a p-dimension column vector, 
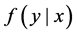is the conditional density function. For the conventional regression models, the mean of 
is usually used to investigate the relationship between 
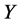and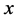 
and the linear regression assumes that the mean of 
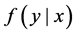is a linear function of
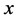. Yao and Li [10] proposed a new regression model called modal linear regression that assumes the mode of 
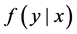is a linear function of the predictor
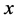. Modal linear regression measures the center using the “most likely” conditional values rather than the conditional average used by the traditional linear regression.
Lee [11] used the uniform kernel and Epanechnikov kernel to estimate the modal regression. However, their estimators are of little practical use because the object function is non-differentiable and its distribution is intractable. Scott [2] mentioned the modal regression, but little methodology is given on how to implement it in practice. Recently, Yao et al. [12] investigated the estimation problem in nonparametric regression using the method of modal regression, and obtained a robust and efficient estimator for the nonparametric regression func- tion. Yao and Li [10] suggested using the Gaussian kernel and developed MEM algorithm to compute modal es- timators for linear models. Their estimation procedure is very convenient to be implemented for practitioners and the result is encouraging for many non-normal error distributions. Yu and Aristodemou [13] studied modal regression from Bayesian perspective. In addition, Zhao, Zhang and Liu [14] considered how to yield a robust empirical likelihood estimation for regression models.
The empirical likelihood method originates from Thomas & Grunkemeier [15] . Owen [16] first proposed the definition of empirical likelihood and expounded the system info of empirical likelihood. Zhu and Ibrahim [17] utilized this method for statistical diagnostic, and they developed diagnostic measures for assessing the influence of individual observations when using empirical likelihood with general estimating equations, and used these measures to construct goodness-of-fit statistics for testing possible misspecification in the estimating equations. Liugen Xue and Lixing Zhu [18] summarized the application of this method.
Over the last several decades, the diagnosis and influence analysis of linear regression model has been fully developed (R. D. Cook and S. Weisberg [19] , Bo-cheng Wei, Go-bin Lu & Jian-qing Shi [20] ). So far the statistical diagnostics of modal linear regression models based on empirical likelihood method has not yet been seen in the literature. This paper attempts to study it.
The rest of the paper is organized as follows. In Section 2, we review the modal regression. In Section 3, empirical likelihood and estimation equation are presented. The main results are given in Section 4. Simulation study is given to illustrate our results in Section 5.
2. Modal Linear Regression
Suppose a response variable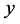 
given a set of predictor 
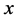is distributed with a probability density function (PDF)
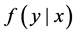. Yao and Li [10] proposed to use the mode of
, denoted by
, to investigate the relationship between 
and![]()
. The proposed modal linear regression method assumes that
![]()
. (1)
The idea of modal linear regression can be easily generalized to other models such as nonlinear regression, nonparametric regression, and varying coefficient partially linear regression. To include the intercept term in (1), we assume that the first element of ![]()
is 1. Let ![]()
and denote by ![]()
the conditional density of ![]()
given![]()
. Here, we allow the conditional density of ![]()
given ![]()
to depend on![]()
. Based on the model assumption (1), one knows that ![]()
is maximized at 0 for any x. If ![]()
is symmetric about 0, the ![]()
in (1) will be the same as the conventional linear regression parameters. However, if ![]()
is skewed, they will be different and it is even possible that the modal regression is a linear function of ![]()
but the conventional mean regression function is nonlinear.
Yao and Li [10] proposed to estimate the modal regression parameter ![]()
in (1) by maximizing
![]()
(2)
where ![]()
and ![]()
is a kernel density function. Denote by ![]()
the maximizer of (2). We call ![]()
the modal linear regression (MODLR) estimator.
3. Empirical Likelihood and Estimation Equation
In this section, we review empirical likelihood based on modal regression for regression coefficients, then establish the estimation equations.
Similarly to Zhao, Zhang and Liu [14] , we define an auxiliary random vector
![]()
. (3)
Note that![]()
, where ![]()
is the true parameter value. According to the empirical likelihood principle, we define the empirical likelihood ratio function of ![]()
to be
![]()
. (4)
By the method of Lagrange multipliers, similar to that used in Owen (2001), ![]()
is well-defined and can be re-expressed as
![]()
, (5)
where ![]()
is determined by the constraint equation
![]()
Motivated by Zhu and Ibrahim [17] , we regard ![]()
and ![]()
as independent variables and define
![]()
,
Obviously, the maximum empirical likelihood estimates ![]()
and ![]()
are the solutions of following equations:
![]()
4. Local Influence Analysis of Model
We consider the local influence method for a case-weight perturbation![]()
, for which the empirical log-
likelihood function ![]()
is defined by![]()
. In this case, ![]()
, defined to be an n ×
1 vector with all elements equal to 1, represents no perturbation to the empirical likelihood, because
![]()
. Thus, the empirical likelihood displacement is defined as![]()
,
where ![]()
is the maximum empirical likelihood estimator of ![]()
based on![]()
. Let ![]()
with ![]()
and![]()
, where ![]()
is a direction in![]()
. Thus, the normal curvature of the in-
fluence graph ![]()
is given by![]()
, where
![]()
, in which ![]()
is a ![]()
matrix with
![]()
-th element given by![]()
.
We consider two local influence measures based on the normal curvature ![]()
as follows. Let
![]()
be the ordered eigenvalues of the matrix ![]()
and let
![]()
be the associated orthonormal basis, that is,![]()
. Thus, the spectral decomposition of ![]()
is given by
![]()
The most popular local influence measures include![]()
, which corresponds the largest eigen value![]()
, as well
as![]()
, where ![]()
is an ![]()
vector with ![]()
-th component 1 and 0 otherwise. The ![]()
represents
the most influential perturbation to the empirical likelihood function, whereas the ![]()
-th observation with a large ![]()
can be regarded as influential.
As the discuss of Zhu et al. [17] , for varying-coefficient density-ratio model, we can deduce that
![]()
(4)
where ![]()
![]()
![]()
![]()
![]()
.
5. Numerical Study
We generate data-sets from following model
![]()
where the covariates ![]()
follows a three-dimensional normal distribution ![]()
with unit marginal variance and correlation 0.5. The true value of the regression coefficient is
![]()
. The error ![]()
is independent of![]()
. For ease of computation, we use the standard normal density function for![]()
. Simulation results are computed based on 1000 random samples with the sample size being 150.
In order to check out the validity of our proposed methodology, we change the value of the first, 125th, 374th, 789th and 999th data. For every case, it is easy to obtain![]()
. For ![]()
and![]()
, using the samples, we evaluated their maximum empirical likelihood estimators.
Consequently, it is easy to calculate the value of ![]()
and![]()
. The result of ![]()
is as Figure 1.
From the figure, we can see that in most cases, the value of ![]()
are reasonably close to one fixed value. Following the definition and properties of![]()
, we can diagnose the strong influence points, the value of which deviate from the average seriously. It can be seen from the result of ![]()
that the first, 125th, 374th, 789th and 999th data are strong influence points. Indeed, our results are illustrated.
6. Discussion
In this paper, we considered the statistical diagnosis for modal linear regression models based on empirical likelihood. Through simulation study, we illustrate that our proposed method can work fairly well.