New Method of Givens Rotations for Triangularization of Square Matrices ()
1. Introduction
In linear algebra, methods of QR-decomposition (or factorization) of a nonsingular matrix into a unitary matrix and a triangular matrix are well known in mathematics [1] -[3] . QR-decomposition is used in many applications in computing and data analysis. This is the problem of solution of a linear system of equations written in matrix form as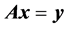 . The solution
. The solution 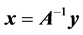 can be found after the factorization of the matrix
can be found after the factorization of the matrix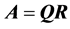 , where
, where 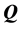 is an orthogonal matrix
is an orthogonal matrix 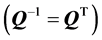 and
and 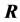 is a right triangular matrix, in the case when the dimensions of the known vector
is a right triangular matrix, in the case when the dimensions of the known vector 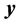 and unknown
and unknown 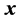 are equal. This QR-decomposition is unique if the diagonal coefficients of the matrix
are equal. This QR-decomposition is unique if the diagonal coefficients of the matrix 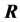 are positive. In this case,
are positive. In this case, 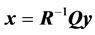 , or
, or 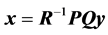 in the rank-revealing QR algorithm, when the diagonal elements of the matrix
in the rank-revealing QR algorithm, when the diagonal elements of the matrix 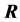 are permuted
are permuted 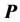 in the non-increasing order. There are several methods for computing the QR-decomposition, such as the Gramm-Schmidt process and method of Cholesky factorization. We here mention two other methods: the Householder transformations (known also as Householder reflections) and the Givens rotations. In the second method, each rotation zeros one element in the subdiagonal of the matrix. Therefore, a sequence of
in the non-increasing order. There are several methods for computing the QR-decomposition, such as the Gramm-Schmidt process and method of Cholesky factorization. We here mention two other methods: the Householder transformations (known also as Householder reflections) and the Givens rotations. In the second method, each rotation zeros one element in the subdiagonal of the matrix. Therefore, a sequence of 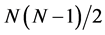 plane rotations is required for reduction of a square matrix
plane rotations is required for reduction of a square matrix 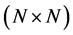 to triangular form. The Givens rotations require a large number of arithmetical operations, including multiplications and
to triangular form. The Givens rotations require a large number of arithmetical operations, including multiplications and 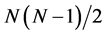 square roots [4] . The method of Householder transforms is the most applied method for QR-decomposition, which reduces the number of square roots to at most
square roots [4] . The method of Householder transforms is the most applied method for QR-decomposition, which reduces the number of square roots to at most 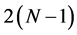 and uses about
and uses about 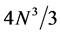 multiplications [5] -[8] .
multiplications [5] -[8] .
In this paper, a new look on the application of Givens rotations to the QR-decomposition problem is described, which is similar to the method of Householder transformations. The concept of the discrete heap transform is applied, which has been introduced in digital signal processing to generate the signal-induced unitary transforms by Grigoryan [9] -[12] . Both cases of real and complex matrices are considered and examples of performing the QR-decomposition of matrices are given. We also illustrate the importance of the path of the heap transform in such decomposition. The traditional way of consequently performing the rotations of data in natural order 1,2,3,... is not the best way, or path, in calculating the QR-decomposition. We briefly describe other more effective paths in QR-decomposition by the heap transforms and give a comparison with the known method of the Householder transformation.
2. Transforms with Decision Equations
Let 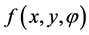 and
and 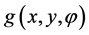 be functions of three variables;
be functions of three variables; 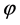 is referred to as the rotation parameter such as the angle, and x and y as the coordinates of the point
is referred to as the rotation parameter such as the angle, and x and y as the coordinates of the point 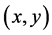 on the plane. These variables may have other meanings. The function
on the plane. These variables may have other meanings. The function 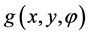 is parameterized and it is assumed that for a specified set of numbers a and for each point
is parameterized and it is assumed that for a specified set of numbers a and for each point 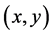 on the plane (or its chosen subset) the equation
on the plane (or its chosen subset) the equation
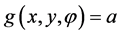 (1)
(1)
has a unique solution with respect to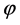 . We denote the solution of this equation by
. We denote the solution of this equation by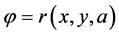 . The system of equations
. The system of equations 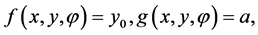 is called the system of decision equations. The value of
is called the system of decision equations. The value of 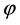 is calculated from the second equation which is called the angular equation. Then the value of
is calculated from the second equation which is called the angular equation. Then the value of 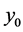 is calculated from the given input
is calculated from the given input 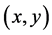 and
and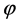 . It is also assumed that the two-dimensional transformation
. It is also assumed that the two-dimensional transformation
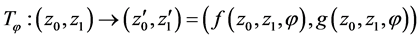
which is derived (or whose matrix is calculated) from the given decision equations by 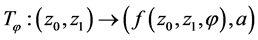 is unitary. These transformations are basic stones to build unitary transforms.
is unitary. These transformations are basic stones to build unitary transforms.
Figure 1 shows the graph of such a basic transformation in part a. The transformation 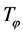 is defined by given
is defined by given  and
and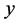 , namely, the angle
, namely, the angle 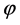 is calculated first and then the transform
is calculated first and then the transform 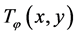 is calculated. The second output is shown with the dash arrow, since the value of this output equals
is calculated. The second output is shown with the dash arrow, since the value of this output equals 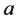 which is known from given angular Equation (1). The graph of this transform applied to an input
which is known from given angular Equation (1). The graph of this transform applied to an input 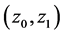 is shown in part b.
is shown in part b.
Example 1: (Elementary rotation). Given a real number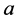 , we consider the following functions:
, we consider the following functions:

(a) Y-operator (b) X-operator
Figure 1. Graphs of the basic transform 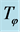 defined (a) by a point
defined (a) by a point 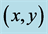 and applied (b) on an input
and applied (b) on an input .
.
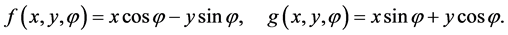
The basic transformation is defined as a rotation of the point 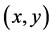 to the horizontal
to the horizontal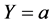 ,
,
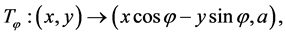
where the rotation angle 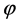 is calculated by
is calculated by 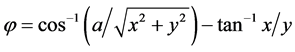 and
and 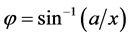 if
if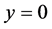 . The angular equation puts a constrain on parameter a, namely, it is required that
. The angular equation puts a constrain on parameter a, namely, it is required that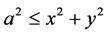 .
.
3. Discrete Heap Transforms
The composition of the N-dimensional discrete heap transform by a given vector-generator 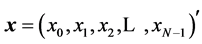 is performed by the sequential calculation of basic two-dimensional transformations. In matrix form, this composition can be written as follows:
is performed by the sequential calculation of basic two-dimensional transformations. In matrix form, this composition can be written as follows: 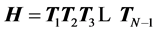 where each transformation
where each transformation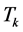 ,
, 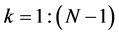 , changes only two components of the input. We assume that the components of an input
, changes only two components of the input. We assume that the components of an input 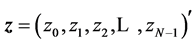 are processed in order
are processed in order 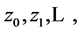 and
and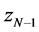 . This is a natural path
. This is a natural path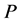 , and in general, such a path can be taken in many different ways. It is a very important characteristic of the heap transform and the right selection of the path leads to an effective application of the transform in calculating the QR-decomposition. We consider the case, when all basic transformations
, and in general, such a path can be taken in many different ways. It is a very important characteristic of the heap transform and the right selection of the path leads to an effective application of the transform in calculating the QR-decomposition. We consider the case, when all basic transformations 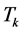 are parameterized by angles
are parameterized by angles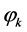 . The special selection of a set of parameters is initiated by the vector-generator
. The special selection of a set of parameters is initiated by the vector-generator 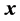 through the decision equations with a given set of constants
through the decision equations with a given set of constants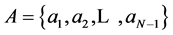 . The generator is processed first, and during this process all required angles are calculated. For a given set A, we define the following “heap” of elements:
. The generator is processed first, and during this process all required angles are calculated. For a given set A, we define the following “heap” of elements:
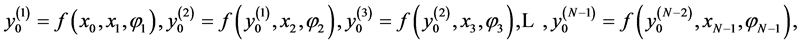
where angles 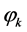 are calculated by
are calculated by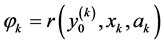 ,
, 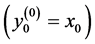 , and
, and 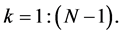 Thus, it is assumed that the first component of the vector participates in calculations of all
Thus, it is assumed that the first component of the vector participates in calculations of all 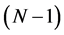 basic transforms
basic transforms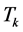 . As an example, Figure 2 shows the signal-flow graph of determination of the five-point transform by a vector
. As an example, Figure 2 shows the signal-flow graph of determination of the five-point transform by a vector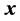 .
.
The N-point transformation 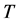 composing from
composing from 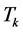 in the space of N-dimensional vectors
in the space of N-dimensional vectors  is defined as
is defined as
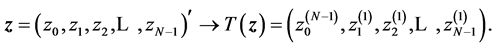
Values of the components 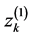 are calculated by
are calculated by
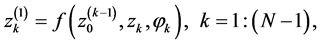
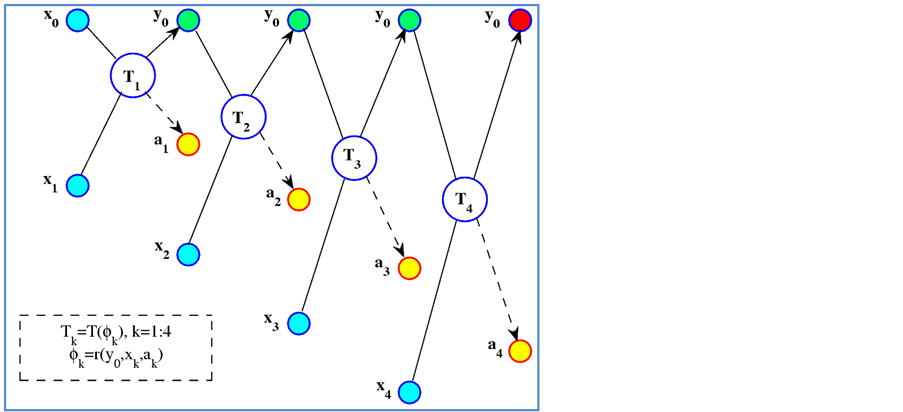
Figure 2. Signal-flow graph of determination of the five-point transform by a vector .
.
where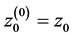 . The first component is transformed sequentially as
. The first component is transformed sequentially as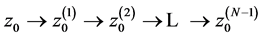 where
where 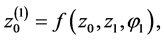
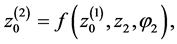 ×××,
×××, 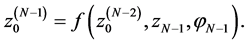 The following should be mentioned about the heap transform. The transform is performed in a space of N-dimensional vectors
The following should be mentioned about the heap transform. The transform is performed in a space of N-dimensional vectors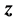 , but all angles
, but all angles 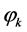 are found and the transformation
are found and the transformation 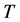 is composed after solving the decision equations relative to a given vector-generator
is composed after solving the decision equations relative to a given vector-generator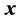 . The transform of
. The transform of 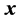 results in a vector with the constant components of the set A, plus
results in a vector with the constant components of the set A, plus 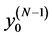 as the first component,
as the first component,
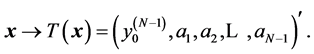
The transformation 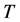 is called the N-point discrete
is called the N-point discrete 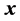 -signal-induced heap transformation (DsiHT), and the vector
-signal-induced heap transformation (DsiHT), and the vector 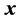 is the generator of this transformation [6] . The first component
is the generator of this transformation [6] . The first component 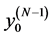 is referred to as the heap of the transform.
is referred to as the heap of the transform.
3.1. Transform Collecting Energy
We focus on the special case of the DsiHT, namely on transformations that collect the energy of vectors in one location. The angular equations for such transformations are defined by the set 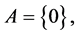 i.e., when
i.e., when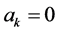 ,
,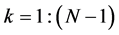 . This condition leads to the fact that the first basis functions of such transforms are the vectorgenerators themselves. Other basis functions are defined based on the correlation data of components of these vectors. Matrices of these transforms are orthogonal. The transforms have simple forms of decomposition that lead to calculation of the N-point transforms with no more than
. This condition leads to the fact that the first basis functions of such transforms are the vectorgenerators themselves. Other basis functions are defined based on the correlation data of components of these vectors. Matrices of these transforms are orthogonal. The transforms have simple forms of decomposition that lead to calculation of the N-point transforms with no more than 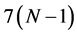 multiplications and
multiplications and 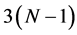 additions.
additions. 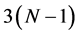 operations are also required for calculating elementary trigonometric functions. In the linear space of N-dimension vectors, we construct such an orthogonal transform,
operations are also required for calculating elementary trigonometric functions. In the linear space of N-dimension vectors, we construct such an orthogonal transform, 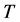 , whose matrix is defined by
, whose matrix is defined by 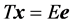 where
where 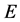 denotes the energy of the vector and
denotes the energy of the vector and 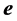 is the unit vector
is the unit vector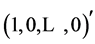 . The term “energy” is referred to as the norm of the vector, i.e.,
. The term “energy” is referred to as the norm of the vector, i.e., 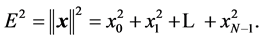 To define the desired transform
To define the desired transform , we consider the following method of energy transferring. Let
, we consider the following method of energy transferring. Let 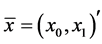 be a 2-D vector to be rotated into a vector
be a 2-D vector to be rotated into a vector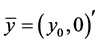 , i.e.,
, i.e., 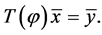
The matrix of the transformation, 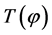 , which is the Givens rotation, is defined by the matrix equation
, which is the Givens rotation, is defined by the matrix equation
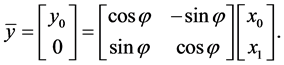 (2)
(2)
The angle 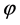 and component
and component 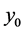 are calculated as
are calculated as 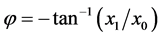 if
if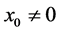 , and
, and
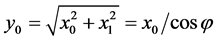 . If
. If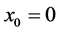 , then
, then 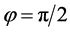 and
and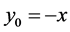 . The energy is collected in the first components,
. The energy is collected in the first components,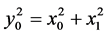 .
.
When processing the N-dimensional vector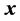 , the first pair of components,
, the first pair of components, 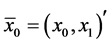 , is transferred to the vector
, is transferred to the vector 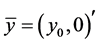 by Equation (2), as the point
by Equation (2), as the point 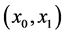 is rotated to the point
is rotated to the point 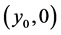 on the horizontal line. Then, on the next kth step of calculations, when
on the horizontal line. Then, on the next kth step of calculations, when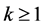 , the similar rotations are accomplished over vectors
, the similar rotations are accomplished over vectors
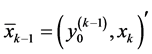 , where
, where 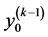 denotes a new value of the first component on the (k − 1)th step, and
denotes a new value of the first component on the (k − 1)th step, and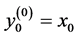 . The value of the first component
. The value of the first component 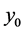 is renewed consequently as
is renewed consequently as
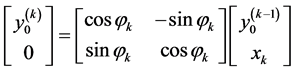 (3)
(3)
where the angles are defined by
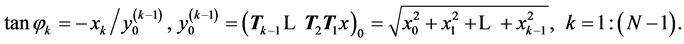 (4)
(4)
Here, 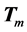 are respectively the matrices of the Givens rotations
are respectively the matrices of the Givens rotations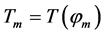 ,
,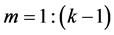 . As a result, the whole energy of the input signal is collected consequently and, then, transferred to the first component
. As a result, the whole energy of the input signal is collected consequently and, then, transferred to the first component
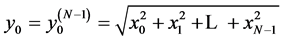
of the transform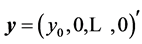 . Figure 3 shows the signal-flow graph of calculation of the four-point trans-
. Figure 3 shows the signal-flow graph of calculation of the four-point trans-

Figure 3.Signal-flow graph of calculation of the four-point heap transform of the vector z.
form of a vector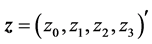 . It is assumed that all parameters
. It is assumed that all parameters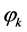 ,
, 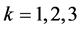 , are calculated by the given vector
, are calculated by the given vector 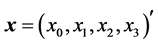 and then used when transforming the vector
and then used when transforming the vector 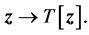
3.2. Analytical Expressions
It is important to note, that the basic transformations, 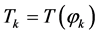 ,
, 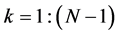 , that compose the N-point DsiHT, can be performed without calculation of angles and trigonometric functions. Analytical formulas can be derived for calculation of components of the heap transform
, that compose the N-point DsiHT, can be performed without calculation of angles and trigonometric functions. Analytical formulas can be derived for calculation of components of the heap transform 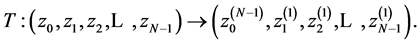 The matrix of the transform can also be calculated analytically. To show this fact, we introduce the following notations which represent respectively the partial cross-correlation of
The matrix of the transform can also be calculated analytically. To show this fact, we introduce the following notations which represent respectively the partial cross-correlation of 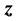 with the vector-generator
with the vector-generator 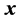 and energy of
and energy of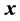 :
:
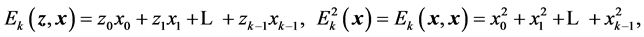
where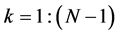 . The components of the heap transform on the kth iteration can be expressed by correlation data as
. The components of the heap transform on the kth iteration can be expressed by correlation data as
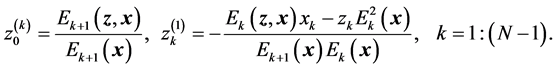 (5)
(5)
On the final step, the value of the first component is defined by 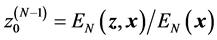 which is the correlation coefficient of the input signal
which is the correlation coefficient of the input signal 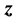 with the normalized signal-generator
with the normalized signal-generator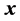 . In the particular
. In the particular 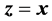 case, we obtain
case, we obtain 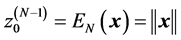 and the rest of coefficients
and the rest of coefficients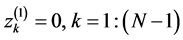 .
.
The coefficients  of the matrix of the N-point DsiHT can be obtained from equations in (5). The mth row of the matrix of the transform is defined by applying the unit vector
of the matrix of the N-point DsiHT can be obtained from equations in (5). The mth row of the matrix of the transform is defined by applying the unit vector 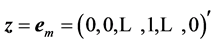 with 1 on the mth position, where integer
with 1 on the mth position, where integer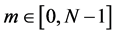 . Therefore, the coefficients can be calculated as
. Therefore, the coefficients can be calculated as
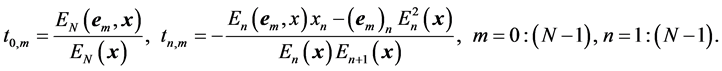 (6)
(6)
4. Transforms with Decision Equations
In this section, we give a brief analysis of the matrix decomposition by the heap transformations and the comparison with the known methods which are based on rotations in two dimensions. It should be noted first that the discrete heap transformations differ from the well-known Householder transformation [2] , whose matrix 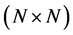 is symmetric and defined as
is symmetric and defined as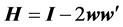 , where the normalized vector
, where the normalized vector 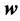 is calculated
is calculated
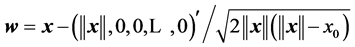
and 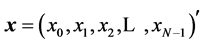 is a given vector. For example, when
is a given vector. For example, when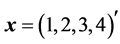 , the Householder vector equals
, the Householder vector equals 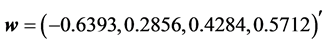 and the matrix of the Householder transform is
and the matrix of the Householder transform is
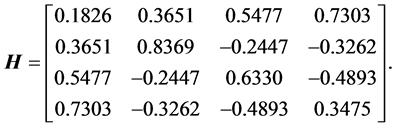
The matrix of the heap transformation generated by the same vector x equals
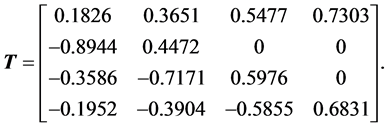
These two transformations result in the same vector, 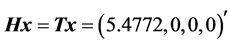 , where
, where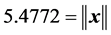 . Both transformations have the same first basis function which equals the normalized vector-generator.
. Both transformations have the same first basis function which equals the normalized vector-generator.
The heap and Householder transformations differ much when considered with the large dimensions. For instance, when 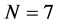 and the vector-generator
and the vector-generator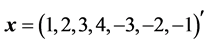 , we obtain the following symmetric matrix of the Householder transformation with determinant one:
, we obtain the following symmetric matrix of the Householder transformation with determinant one:
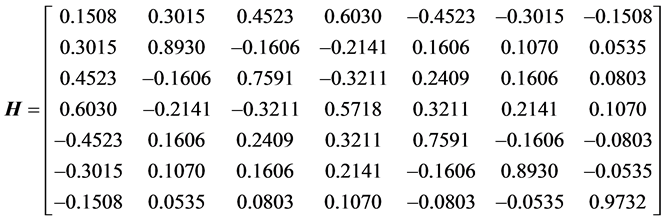
and the vector 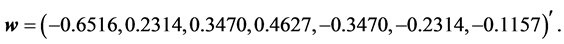 The orthogonal matrix of the heap transformation generated by the vector
The orthogonal matrix of the heap transformation generated by the vector 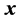 is not full filled and has the zero upper triangular submatrix with 15 zeros,
is not full filled and has the zero upper triangular submatrix with 15 zeros,
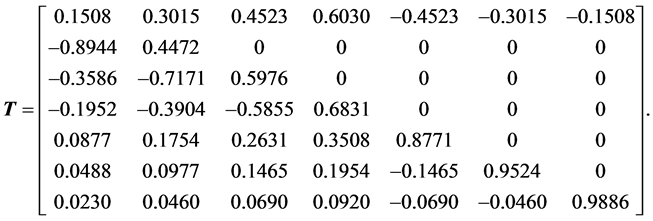
We now illustrate the difference of the DsiHT and Householder transforms applied on signals. Figure 4 shows the example with the 257-point signal 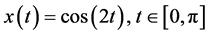 and noisy signal
and noisy signal
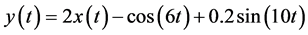 in part a, along with the
in part a, along with the 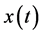 -induced heap and Householder transforms
-induced heap and Householder transforms
of 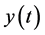 respectively in b and c, and the difference of these two transforms in d. The first seven values of the Householder and heap transforms are the following:
respectively in b and c, and the difference of these two transforms in d. The first seven values of the Householder and heap transforms are the following:
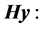 22.6276, −1.0608, −1.0285, −0.9915, −0.9503, −0.9052, −0.8568,
22.6276, −1.0608, −1.0285, −0.9915, −0.9503, −0.9052, −0.8568,
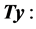 22.6276, 0.0190, 0.0366, 0.0566, 0.0788, 0.1031, 0.1291.
22.6276, 0.0190, 0.0366, 0.0566, 0.0788, 0.1031, 0.1291.
The big difference of these transforms occurs in the first ninety components.
5. Matrix Decomposition
We now consider the application of heap transforms for calculating the determinant of a nonsingular square matrix, as well as its decomposition. The method described in this section is based on the same idea as the method of Householder transforms, also known as the Householder reflections. Although the heap transformation and Householder transformation are different, it is evident that these two concepts should result in the same (or similar) decomposition, but by different ways.
Let 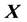 be a real square matrix (N × N) with
be a real square matrix (N × N) with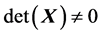 . We denote coefficients of this matrix as
. We denote coefficients of this matrix as
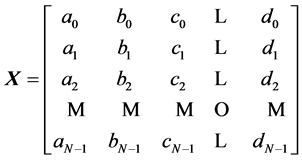 .
.
Let vector 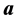 be the first column of this matrix,
be the first column of this matrix,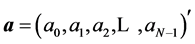 . We denote by
. We denote by 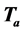 the matrix of the heap transformation
the matrix of the heap transformation 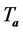 generated by this vector. This matrix contains an upper triangular submatrix with
generated by this vector. This matrix contains an upper triangular submatrix with 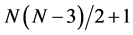 zeros. The product of two matrices
zeros. The product of two matrices 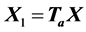 results in a matrix
results in a matrix 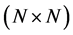 with the first column equal to
with the first column equal to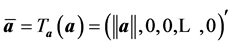 . Therefore, the matrix
. Therefore, the matrix 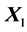 has the following form:
has the following form:
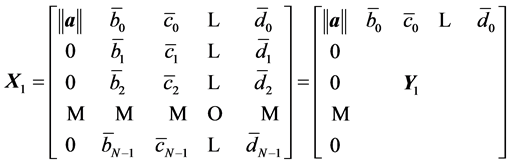
where we denote by 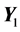 the
the 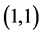 minor of this product. We can repeat the described above process for the submatrix
minor of this product. We can repeat the described above process for the submatrix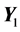 , by considering its first vector-column
, by considering its first vector-column 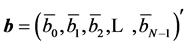 as a generator for the
as a generator for the 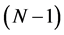 - point heap tranformation
- point heap tranformation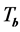 , whose matrix we denote by
, whose matrix we denote by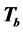 . The product of two matrices
. The product of two matrices
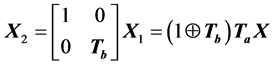
is a matrix (N × N) with the second column equal
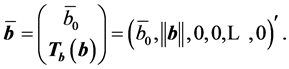
On this step, the matrix 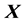 is transformed to the matrix
is transformed to the matrix 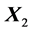 which has the following form:
which has the following form:
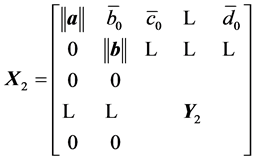
where 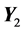 is the (2,2) minor of this product and has the size
is the (2,2) minor of this product and has the size 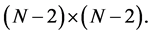
On the next step, we consider the first vector c of the submatrix 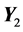 and construct the matrix
and construct the matrix 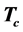 of heap transformation generated by
of heap transformation generated by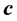 . Then, the (3,3) minor
. Then, the (3,3) minor 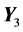 of the product of the matrices
of the product of the matrices
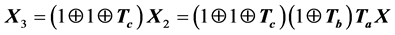
is transformed into a matrix whose the first column is zero, except in the first row. The process of such transformations is repeated until we obtain the upper triangular matrix:
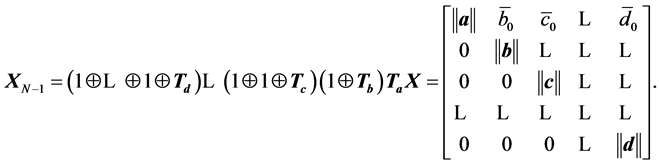
The determinant of the matrix equals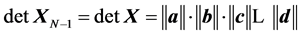 , since all heap transformations have determinant one. Thus, the determinant of a square nonsingular matrix can be calculated by using the heap transforms. We denote by
, since all heap transformations have determinant one. Thus, the determinant of a square nonsingular matrix can be calculated by using the heap transforms. We denote by 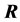 the product of the following matrices
the product of the following matrices
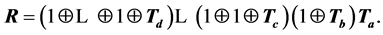
Each heap transformation is unitary, and R is unitary. The inverse matrix 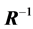 can thus be represented by
can thus be represented by
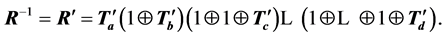
We obtain the following decompositions of the matrix 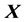 and its inverse:
and its inverse: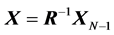 ,
, 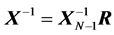 , where
, where 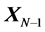 and
and 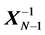 are the upper triangular matrices, and
are the upper triangular matrices, and 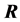 is unitary.
is unitary.
Example 2: Consider the decomposition of the following matrix (3 × 3):
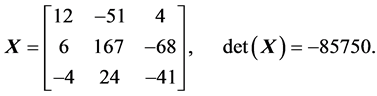
The decomposition of 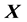 by the heap transforms,
by the heap transforms, 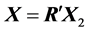 , results in the unitary matrix
, results in the unitary matrix
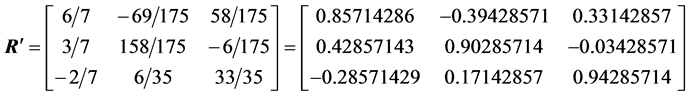
and the upper triangular matrix
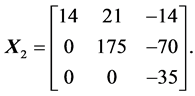
The coefficients of the matrix 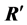 are given with precision of eight digits after the point. The decomposition of the matrix
are given with precision of eight digits after the point. The decomposition of the matrix 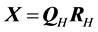 by the Householder transforms is defined by the same matrices,
by the Householder transforms is defined by the same matrices, 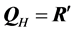 and
and . Thus, by means of the heap transforms which are composed by the Givens rotations, we achieve the same decomposition as the Householder reflections. It should be noted, that the first row-vector of the matrix
. Thus, by means of the heap transforms which are composed by the Givens rotations, we achieve the same decomposition as the Householder reflections. It should be noted, that the first row-vector of the matrix 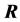 equals to the normalized first column-vector
equals to the normalized first column-vector 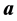 of the original matrix
of the original matrix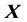 . For the example considered above, we obtain
. For the example considered above, we obtain
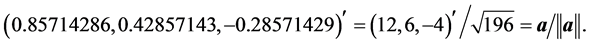
Arithmetic Complexity of the Decomposition
The 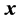 -generated heap transform of a vector
-generated heap transform of a vector 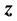 can be calculated by using analytical Equations (5) and (6),
can be calculated by using analytical Equations (5) and (6),
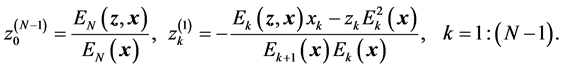 (7)
(7)
The calculation of all energy coefficients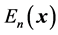 ,
, 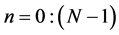 , requires
, requires 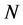 multiplications. The total number of multiplications is calculated by
multiplications. The total number of multiplications is calculated by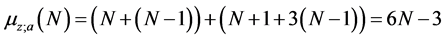 , plus
, plus 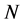 square roots. When the matrix
square roots. When the matrix 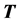 is multiplying by another square matrix, the number of required multiplications can be calculated as
is multiplying by another square matrix, the number of required multiplications can be calculated as 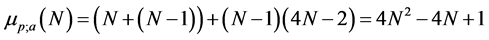 plus
plus 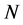 square roots. If we use this estimation to calculate the number of multiplications for factorization of a square nonsingular matrix by heap transforms, we obtain the following number:
square roots. If we use this estimation to calculate the number of multiplications for factorization of a square nonsingular matrix by heap transforms, we obtain the following number:
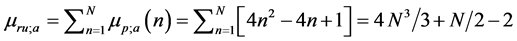
plus 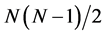 square roots.
square roots.
6. Strong Heap Transform
The point, or the heap, where the energy of the vector-generator is transferred is not required to be at the first location of the signal. The DsiHT can be defined by equation 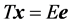 for any unit vector
for any unit vector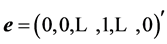 . The path P along which we compose the heap is important, not a location of energy integration, when defining the discrete heap transform. As an example, we consider the basic transforms that sequentially process the last pair of components of the signal. This is the case, when the path P of the heap transformation induced by a vector-signal x is defined as
. The path P along which we compose the heap is important, not a location of energy integration, when defining the discrete heap transform. As an example, we consider the basic transforms that sequentially process the last pair of components of the signal. This is the case, when the path P of the heap transformation induced by a vector-signal x is defined as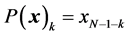 ,
,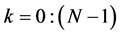 . We call this heap transformation the strong heap transformation. The energy from each component xk is taken away and given to the last component
. We call this heap transformation the strong heap transformation. The energy from each component xk is taken away and given to the last component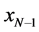 . The strong heap transformation generated by the vector x results in the transform
. The strong heap transformation generated by the vector x results in the transform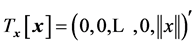 .
.
Example 3: For the vector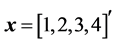 , the matrix of this heap transformation is orthogonal and equals
, the matrix of this heap transformation is orthogonal and equals
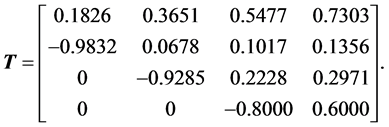
It is interesting to note that the energy of the signal is transferred sequentially to the first component in numbers 5, 5.3852, and 5.4772. This heap of numbers is smaller than the numbers 2.2361, 3.7417, and 5.4772, when the four-point DsiHT is composed along the ordinary path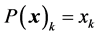 ,
, 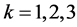 , by Equations (3) and (4). That can be explained because of small values of the first components of the signal
, by Equations (3) and (4). That can be explained because of small values of the first components of the signal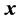 .
.
The method of triangularization of a square nonsingular matrix 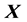 by the strong heap transformations is described similarly to the method described in Section 4 for the ordinary path. The only difference is that on each kth step of calculations, where
by the strong heap transformations is described similarly to the method described in Section 4 for the ordinary path. The only difference is that on each kth step of calculations, where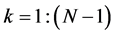 , the generator of the strong heap transformation, which is zeroing the kth column of the renewed matrix
, the generator of the strong heap transformation, which is zeroing the kth column of the renewed matrix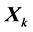 , is taken from the top part of the column. To illustrate this method, we consider the matrix
, is taken from the top part of the column. To illustrate this method, we consider the matrix
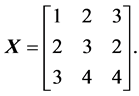
The first column 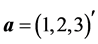 generates the strong heap transformation whose matrix equals
generates the strong heap transformation whose matrix equals
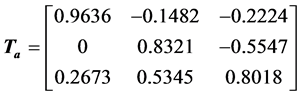
and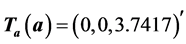 . The product of matrices
. The product of matrices 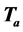 and
and 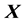 equals
equals
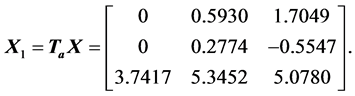
Continuing zeroing the first two elements of the second column of this matrix, by using the strong heap transformation defined by the vector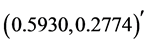 , we obtain the following decomposition of the matrix
, we obtain the following decomposition of the matrix 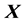 by the product of the unitary matrix
by the product of the unitary matrix 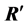 and the lower triangular matrix
and the lower triangular matrix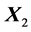 :
:
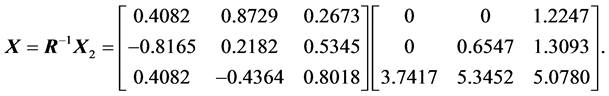 (8)
(8)
The determinant of 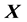 can be calculated as
can be calculated as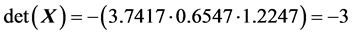 . Thus, we obtain the decomposition of the square matrix
. Thus, we obtain the decomposition of the square matrix 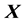 by the product of the unitary matrix
by the product of the unitary matrix 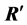 and lower triangular matrix
and lower triangular matrix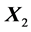 . It should be noted for the comparison that when using the ordinary path,
. It should be noted for the comparison that when using the ordinary path, 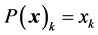 ,
, 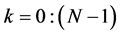 , the following decompositions of the matrix
, the following decompositions of the matrix 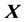 holds:
holds:
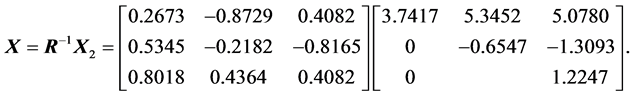
It is evident that there is a relation between this decomposition and the decomposition of Equation (8). The first and third columns of the matrices 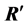 have been rearranged, as well as the first and third rows of the matrices
have been rearranged, as well as the first and third rows of the matrices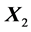 . In addition, the signs of the second column of
. In addition, the signs of the second column of 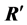 and second row of
and second row of 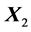 have been changed. Many operations can be saved in the different steps of calculation of the QR-decomposition, if we learn how to select an optimal path in the heap transform. The optimality relates to minimization of the computation complexity of the QR-decomposition.
have been changed. Many operations can be saved in the different steps of calculation of the QR-decomposition, if we learn how to select an optimal path in the heap transform. The optimality relates to minimization of the computation complexity of the QR-decomposition.
Optimal Path of the DsiHT
The path of the heap transformation is an important characteristic of the transformation. In the described above method of QR-decomposition of the matrix by the heap transformations, the ordinary path and path for the strong heap transforms were used. For effective decomposition of non-singular matrices, other well-considered paths 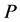 may lead to effective matrix decomposition. The finding such optimal paths is therefore desirable. To illustrate the importance of the path in the heap transformation, we consider the following example with the seven-dimensional vector-generator
may lead to effective matrix decomposition. The finding such optimal paths is therefore desirable. To illustrate the importance of the path in the heap transformation, we consider the following example with the seven-dimensional vector-generator 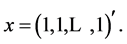 The heap transformation with this generator is defined by the following six steps of calculations (or Givens rotations):
The heap transformation with this generator is defined by the following six steps of calculations (or Givens rotations):
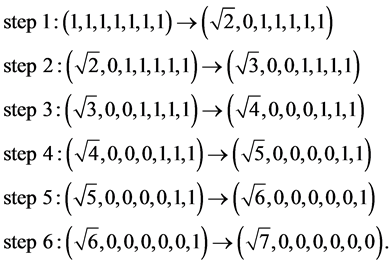
The calculations require six different square roots. Each component of the vector, except the first one, is processed only ones. We now consider another path 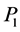 in the heap transformation, which is shown in Figure 5 where the first column corresponds to the generator.
in the heap transformation, which is shown in Figure 5 where the first column corresponds to the generator.
In this path, the transformation rounds three times the components of the input and intermediate data, and on each round a certain number of heaps are calculated, which then are transferred to one heap. During the first round, three different pairs of components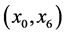 ,
, 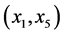 , and
, and 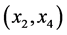 are processed separately and three heaps of value
are processed separately and three heaps of value 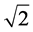 each are calculated, as shown in the second column. Component
each are calculated, as shown in the second column. Component 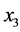 is not used in this stage since the dimension of the input is 7, odd number. In the second round, the first three obtained outputs together with
is not used in this stage since the dimension of the input is 7, odd number. In the second round, the first three obtained outputs together with 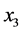 are used to calculate two heaps with values of
are used to calculate two heaps with values of 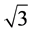 and
and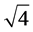 . In the last round, these two heaps are rotated to collect the whole energy
. In the last round, these two heaps are rotated to collect the whole energy 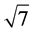 in one heap. The calculation of the heap transform by the path
in one heap. The calculation of the heap transform by the path 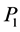 is thus described by six Givens rotations as follows:
is thus described by six Givens rotations as follows:
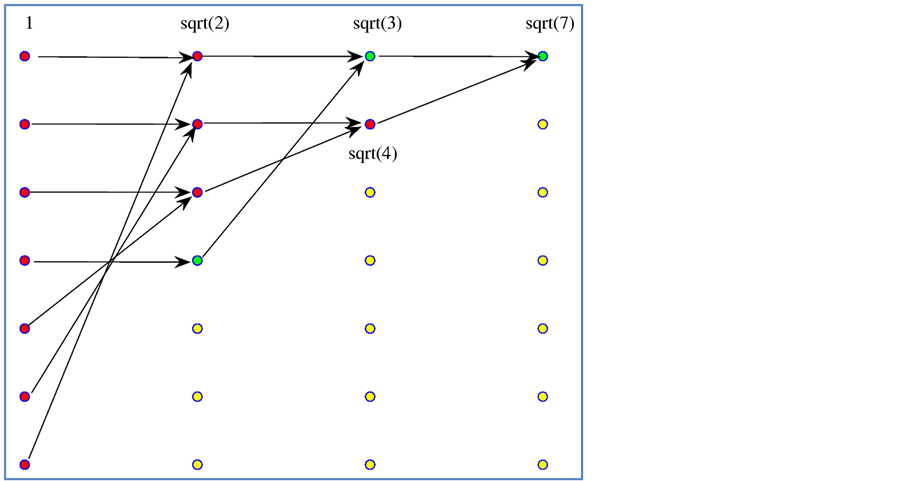
Figure 5. Signal-flow graph of the seven-point heap transformation H .
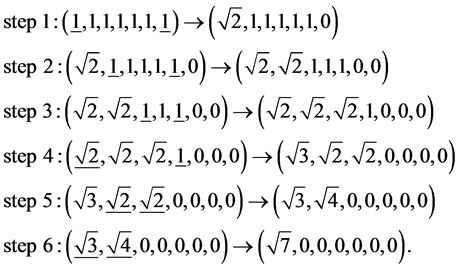
The underlined numbers in the input vectors show the pairs which are used in rotations in each step of calculation. The same number, six, of steps are used to accomplish the heap transform , however there are only four different square roots are calculated,
, however there are only four different square roots are calculated, 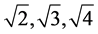 , and
, and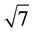 . We can also define such a path for the general
. We can also define such a path for the general 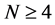 case, by composing first the transformation on the first round as
case, by composing first the transformation on the first round as
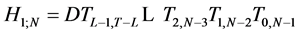
where 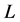 is the integer part of
is the integer part of 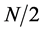 and
and 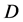 is the empty operator if
is the empty operator if 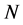 is even, and the identity operator if
is even, and the identity operator if 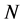 is odd. The transformations
is odd. The transformations 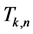 are the Givens rotations of two components of a vector with numbers
are the Givens rotations of two components of a vector with numbers  and
and , when
, when . On the next round, the transform over the first half of outputs is composed similarly,
. On the next round, the transform over the first half of outputs is composed similarly,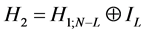 . Continuing this process of transformation until the last round which is completed by the transformation
. Continuing this process of transformation until the last round which is completed by the transformation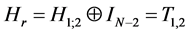 , we obtain the following heap transformation:
, we obtain the following heap transformation: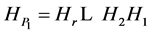 . The number
. The number 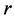 of rounds in the path
of rounds in the path 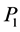 equals the closest integer to
equals the closest integer to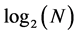 .
.
Example 4: Let 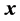 be the vector
be the vector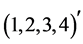 . The signal-flow graph of the heap transformation generated by
. The signal-flow graph of the heap transformation generated by 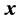 with path
with path 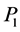 is given in Figure 6.
is given in Figure 6.
The orthogonal matrix of this transformation equals
For comparison, we consider the matrix of the heap transformation defined by the ordinary path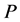 ,
,
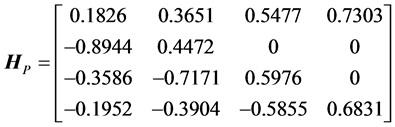
Both transformations result in the same vector,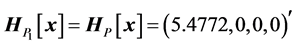 . The matrix
. The matrix 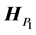 has four zero coefficients which are located symmetrically, and
has four zero coefficients which are located symmetrically, and 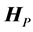 has three zeros composing a triangle.
has three zeros composing a triangle.
Example 5: Let 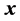 be the vector
be the vector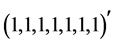 . The signal-flow graph of the heap transformation generated by
. The signal-flow graph of the heap transformation generated by 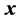 is given in Figure 5. The orthogonal matrix of this transformation equals
is given in Figure 5. The orthogonal matrix of this transformation equals
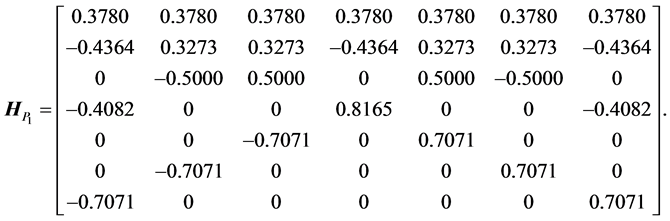
This matrix is symmetric with respect to the middle column, and it has one triangle in the center, which is fully filled by zeros. We also can see two not fully filled by zeros triangles in both sides of the middle column. There are total 22 zeros in these triangles, more than in the matrix of the heap transformation defined by the path P. Indeed, the matrix of this transformation equals
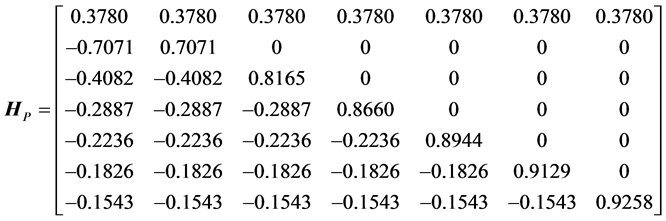
with 15 zero coefficients. Since the matrix 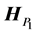 is sparse the application of the heap transformations with the path
is sparse the application of the heap transformations with the path 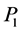 leads to the effective QR-decomposition of non-singular matrices. Indeed, in each step of the decomposition, the use of the heap transformation by the path
leads to the effective QR-decomposition of non-singular matrices. Indeed, in each step of the decomposition, the use of the heap transformation by the path 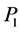 requires fewer operations, when compared with the heap transformation by the path
requires fewer operations, when compared with the heap transformation by the path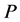 , for large dimensions
, for large dimensions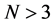 . The matrix of the first transformation is sparser than the second one. For instance, in the (5 × 5) example, total 14 multiplications can be saved when using the paths
. The matrix of the first transformation is sparser than the second one. For instance, in the (5 × 5) example, total 14 multiplications can be saved when using the paths 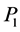 in the QR-decomposition of the matrix
in the QR-decomposition of the matrix 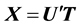 instead of
instead of 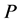 path.
path.
7. Complex DsiHT
In this section, we describe briefly the case when heap transforms are generated by complex vectors and applied on complex vectors. For that we stand on Equation (7) which allows for defining the complex version of the heap transformation. Indeed, we can apply these equations wherein the correlation data are calculated as follows:
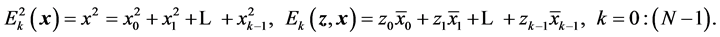
Here, the bar denotes the operation of the complex conjugate. The transformation defined by these equations is unitary and is called the complex heap transformation. The basic two-dimensional transformation T, which is defined by a complex vector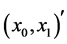 , and then, is applied to a complex input
, and then, is applied to a complex input 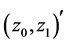 is calculated in matrix form as follows:
is calculated in matrix form as follows:
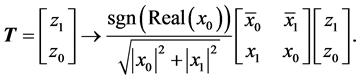
When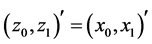 , we obtain the real transform
, we obtain the real transform 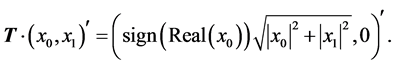 It should be noted that this transformation differs from the known definition of the complex Givens rotation [4] , whose matrix is calculated as
It should be noted that this transformation differs from the known definition of the complex Givens rotation [4] , whose matrix is calculated as
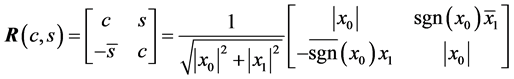
where the complex sign function is defined by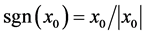 . This rotation results in the following complex transform
. This rotation results in the following complex transform 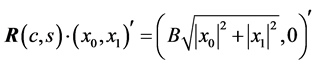 where
where 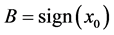 is a complex number with norm one.
is a complex number with norm one.
Example 6: Let 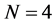 and let the complex vector
and let the complex vector 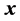 to be
to be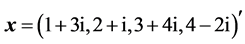 . The complex heap transformation generated by this vector has the following matrix:
. The complex heap transformation generated by this vector has the following matrix:
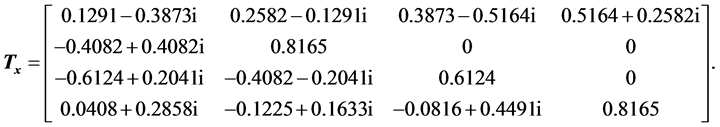
The transform of the vector-generator equals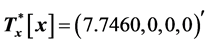 , where
, where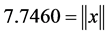 . The matrix
. The matrix 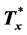 is the complex conjugate to
is the complex conjugate to 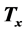 and its first row is the normalized generator, i.e.,
and its first row is the normalized generator, i.e., 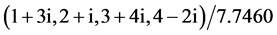 . The complex heap transformations can be used for triangularization of the square complex matrix in a way similar to the real case described above. As an example, we consider the following matrix:
. The complex heap transformations can be used for triangularization of the square complex matrix in a way similar to the real case described above. As an example, we consider the following matrix:
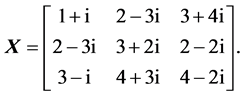
The method of heap transforms results in the following decomposition of 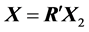 where
where 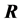 is the unitary matrix
is the unitary matrix
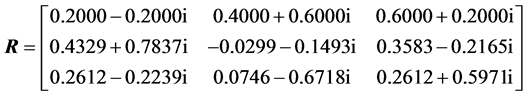
and 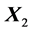 is the upper triangular matrix
is the upper triangular matrix
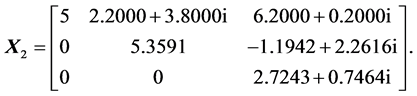
8. Conclusion
A novel decomposition of nonsingular real and complex matrices by fast heap transforms has been described, when the paths 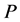 of the transforms are natural. The path of the heap transform is an important characteristic of the transform, and other paths
of the transforms are natural. The path of the heap transform is an important characteristic of the transform, and other paths 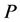 can be found, that may result in more sparse matrices than the path
can be found, that may result in more sparse matrices than the path 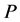 does. The application of such paths will lead to effective matrix decomposition, as shown on examples with the strong heap transform. We have considered only the case of nonsingular matrices of square size. However, the calculations presented above can be applied to the case of non square matrices, as well.
does. The application of such paths will lead to effective matrix decomposition, as shown on examples with the strong heap transform. We have considered only the case of nonsingular matrices of square size. However, the calculations presented above can be applied to the case of non square matrices, as well.