1. Introduction
During the last thirty years, we have searched, unsuccessfully in the history of human knowledge of the universe, if the dynamics criteria had been applied before. As a consequence, we believe that this novel proposal on dynamics interactions, will allow a better understanding of the behavior of celestial systems, for instance, the structure of the asteroid belt, the Kuiper belt or the scattered disc.
In an article published in World Journal of Mechanics [1] (Figure 1), I suggested new ideas to explain the mechanical behavior of macroscopic bodies, and showed evidence that there exists an unstructured area under the present general assumptions of classical mechanics, especially in the case of rigid bodies exposed to simultaneous non coaxial rotations. To address this issue, I proposed new dynamics hypotheses that lead to interesting results and numerous noteworthy scientific and technological applications. I constructed a new mathematical model in rotational field dynamics, and through this model, results based on a rational interpretation of the superposition of motions caused by torques were ob-

Figure 1. Cover page of the magazine World Journal of Mechanics which includes the article: Analysis of Dynamics Fields in No inertial Systems [1], and in which the figure of one of the prototypes used by the author of the experimental tests appears.
tained. For this purpose, I analyzed velocity and acceleration fields that are generated in an object with intrinsic angular momentum, and assessed new criteria for coupling velocities.
I conducted various experiments which confirmed the theory proposed. The experiments have been analyzed and explained in a video accompanying the text: “New Dynamic Hypotheses” [2].
In this paper I will discuss the reactions and inertial fields that cannot be explained by classical mechanics.
At the time of this publication, we had no knowledge of any parallel study on the topic and the findings were evident in the paper, which prevented us from making additional theoretical comparisons or direct readers to other sources to compare criteria.
2. New Experimental Evidences
In May 2013, a new article was published in the same journal, the World Journal of Mechanics, presented by the investigator Luis A. Pérez, with new experimental evidence confirming the thesis mentioned above. In Luis A. Pérez’s article [3], the author corroborated the hypothesis of the Theory of Dynamics Interactions, by new experimental tests he designed. This hypothesis holds that the mechanical behavior of macroscopic bodies in a non-inertial environment open up new assumptions and conclusions on inertial fields and rotational dynamics.
The author first became aware of my proposals of the Theory of Dynamic Interactions through my 2006 article on Saturn’s planet rings, which suggested unsolved phenomena in rotational dynamics and the raising of a novel theory [4]. Intuitively, L. A. Perez realized that the cosmos is mechanical from its smallest to its widest comprehensible appreciation. If material behavior is mechanical everywhere and at any time, from a subatomic particle, wave or string, to a cluster of galaxies, then our assessments could be believed to adhere to with the Laws of Motion.
If the mechanical behavior of the mass is constant everywhere and at any time, from a subatomic particle, to a cluster of galaxies, then our proposals could be believed to be consistent with the laws of motion observed.
An associated video with experiments was presented to support the discussion in the paper: Reflecting new evidences on Rotational Dynamics [5]. In this new video presented by the investigator Luis A. Pérez, new experimental tests are shown which, again, confirm the proposed dynamic theory.
The author states: I read the referred article with some scepticism... However, the subject was so interesting to me that I designed my own experimental tests with the purpose of achieving a clearer cut inertial mobile. And he adds at the end of the video: … The new dynamic hypotheses, proposed by Professor Gabriel Barceló, are thus empirically demonstrated...
3. Dynamics Interactions
During the last thirty years, I have carried out a private and independent project regarding rotational dynamics. The result has been the conception of an innovative theory of dynamics systems, applicable to non-inertial rigid systems in rotation, and specifically, to astrodynamics and galactic astronomy.
3.1. Precedents
According to our records, it was M. E. Jouffret [6], in the 19th C., who first conducted the dynamic analysis of the reactions developed by a particle of a rigid solid with intrinsic rotation which is simultaneously caused to turn around a new axis.
However, in line with this analysis, M. Hirn [7] stated that the variation of the relative position of the particles due to a new rotation on an axis different from the existing one, generated a variation in the distribution of its velocities, giving as a result that this distribution was not uniform for all the particles of the disc situated in the same radius. That instant variation creates a distribution of acceleration in the disc, which we identified with the appearance of inertial effective forces. The questions I asked myself were the following:
• Why is this distribution of accelerations not modeled in classic mechanics?
• Can these criteria be applied to the dynamics of the systems of the universe?
Subsequently, it seems that the studies of rotational dynamics lost interest, probably due to the amazing development of theoretical physics at the beginning of the 20th C. and were thus soon forgotten.
However, I took up those dynamics studies again, in order to better understand the dynamic behavior of rigid solid bodies submitted to different non-coaxial velocities by rotation.
3.2. Axioms
Starting from new dynamics axioms, I developed a conceptual structure which we named Theory of Dynamic Interactions, and which allows to establish new behavior laws of dynamic systems submitted to accelerations by rotation and, which is more specifically, applicable to astrodynamics.
These axioms [8] start from the rotation concepts of space and the anisotropic dynamic fields which are generated when a body is subjected to simultaneous noncoaxial rotations. It incorporates the concept of Dynamic interactions, as the result of a non-discriminating coupling and differentiated, from the different existing dynamic fields.
For example, and as opposed to the classical criteria of Poinsot [9], the field of anisotropic velocities generated by applied torques, is dynamically coupled to the field of translation speeds, generating a new path of the mobile. If the applied torque is constant, this coupling generates a closed orbital path. On the contrary, the field of intrinsic rotation speeds of the body is not coupled to any other field, maintaining the intrinsic rotation constant. Is not this the behavior of the celestial bodies which orbit and rotate simultaneously?
The Theory of Dynamic Interactions generalizes the inertial concepts and phenomena, including them in a unified structure of a new rotational dynamics of fields for non-inertial systems. It is applicable to celestial bodies and has been described in scientific articles and during presentations in international congresses [8,10].
3.3. Equation
Starting from these axioms and the principle of conservation of movement, a mathematical model and some behavior laws have been developed regarding this theory of dynamic systems.
The result is a non-differential equation [10], which determines the velocity of the orbitation in function of the initial speed and the new applied torque M′, being I the momentum of inertia and ω the angular speed of intrinsic rotation of the mobile.
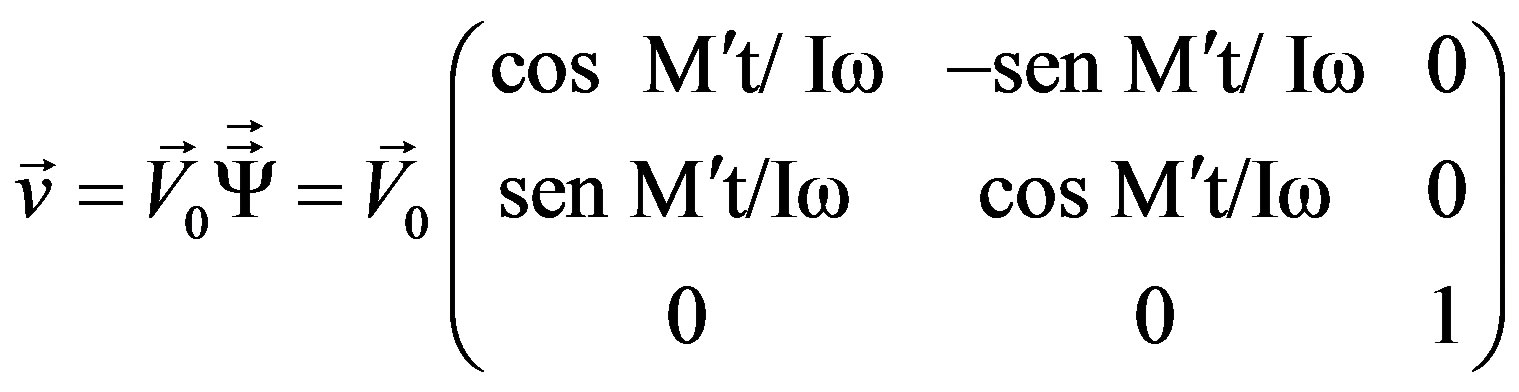 (1)
(1)
The rotational operator  transforms, through one rotation, the initial speed vector
transforms, through one rotation, the initial speed vector  into the speed vector
into the speed vector , both always situated on an identical plane.
, both always situated on an identical plane.
To comprehend this model, we need to understand that, given a body in space with traslation speed and stable rotation around a main axis, the rotational inertia of the body prevents a composition of rotations in such a way that, if a new momentum, non coaxial with the existing rotation acts, the initial rotation will be maintained, and the body will react by modifying its path, initiating an orbit.
The final result is that the initial rotation is constant, whereas the traslational velocity of the center of mass is coupled to the velocity field created by the new torque, not coaxial, generating a new path equivalent to that resulting from the presence of a central force: the body will behave as if it were apparently subjected to a central force, which does not exist.
This equation of movement defines a dynamic model which is clearly different from the one held by classical mechanics, and which allows us to conceive a non-Newtonian rotational dynamics, sustained by the Theory of Dynamic Interactions, based on the hypotheses referred to.
We propose that the Theory of Dynamic Interactions supports the validity of the laws of Newton when these refer to the behavior of matter only in inertial, non-accelerated systems. In addition, we assume that the laws of classical mechanics, totally valid and proved, are exclusively refer to assumptions of translation movements in systems not accelerated by rotation.
3.4. Theory of Dynamic Interactions: Application to Celestial Mechanics
The Theory of Dynamic Interactions is based on the field theory and a non-discriminating coupling of the dynamic fields that are generated in the bodies. Thanks to this field theory, it is possible to find new areas of investigation in a new rotational dynamics of non-inertial systems. The resulting deductions of these rotational dynamics can be relevant for certain problems of the dynamics of the cosmos which are still pending to be solved. This dynamics model can be applied to many assumptions of astrodynamics.
The results of the simulation of this model have been displayed by means of a computer program, proving how a trajectory in space can change when the translation speed or the acting torque varies, obtaining different paths. For example, a spiral orbit is obtained as that in Figure 2, when the translation speed is constantly accelerated, and the torque acting remains constant. This trajectory reminds of the arms of spiral galaxies.
In a published article about the anomalies of the Pioneer probes [11], the application of this mathematical model and of these dynamics hypotheses has also been
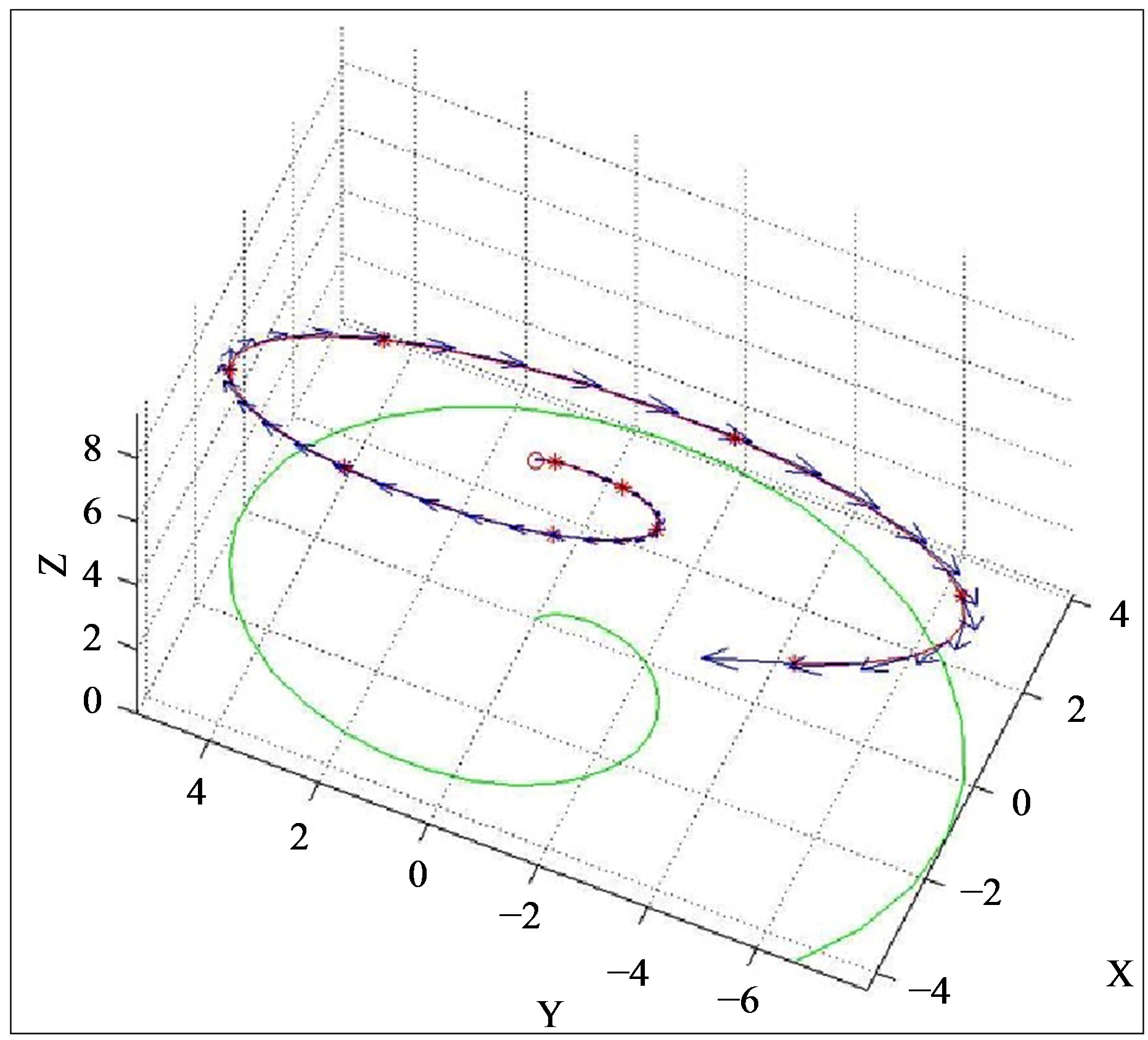
Figure 2. Trajectory of the mass’ center of a moving body, obtained via computer simulation, according to the Theory of Dynamic Interactions where the applied momenta are constant and the translation speed of the moving object is regularly accelerated.
suggested in order to comprehend the anomalous behavior of the probes.
The deviation of the trajectory is caused by the dynamic interaction resulting from the coupling of the linear kinetic momentum of the moving body, with the distribution of velocities generated by the action of the noncoaxial torque.
Our theory is also justified by the behavior of mobiles in space which modify their path without the existence of a resultant of external forces as is the case for the spinning top, the boomerang or the roll coupling of planes.
Supposing that the celestial body, with intrinsic rotation is submitted to an external torque, non coaxial with that rotation, and if both are maintained constant in time, the result of our model will be a closed orbit (Figure 3), equivalent to the one of planetary systems. When we project this path to three reference planes, we can verify that the generated orbit is flat (Figure 4).
4. History of Cosmology
When I first conceived this theory of rotational dynamics for systems accelerated by rotations, I noticed that in celestial systems there happened to be bodies that simultaneously orbit and rotate on their axis without this characteristic having been recognized as a behavior law, at least not up to date. Interested by this, I initiated an analysis of the history of cosmology in order to confirm that this dynamic constant and my own hypothesis had not been proposed before. While studying the evolution
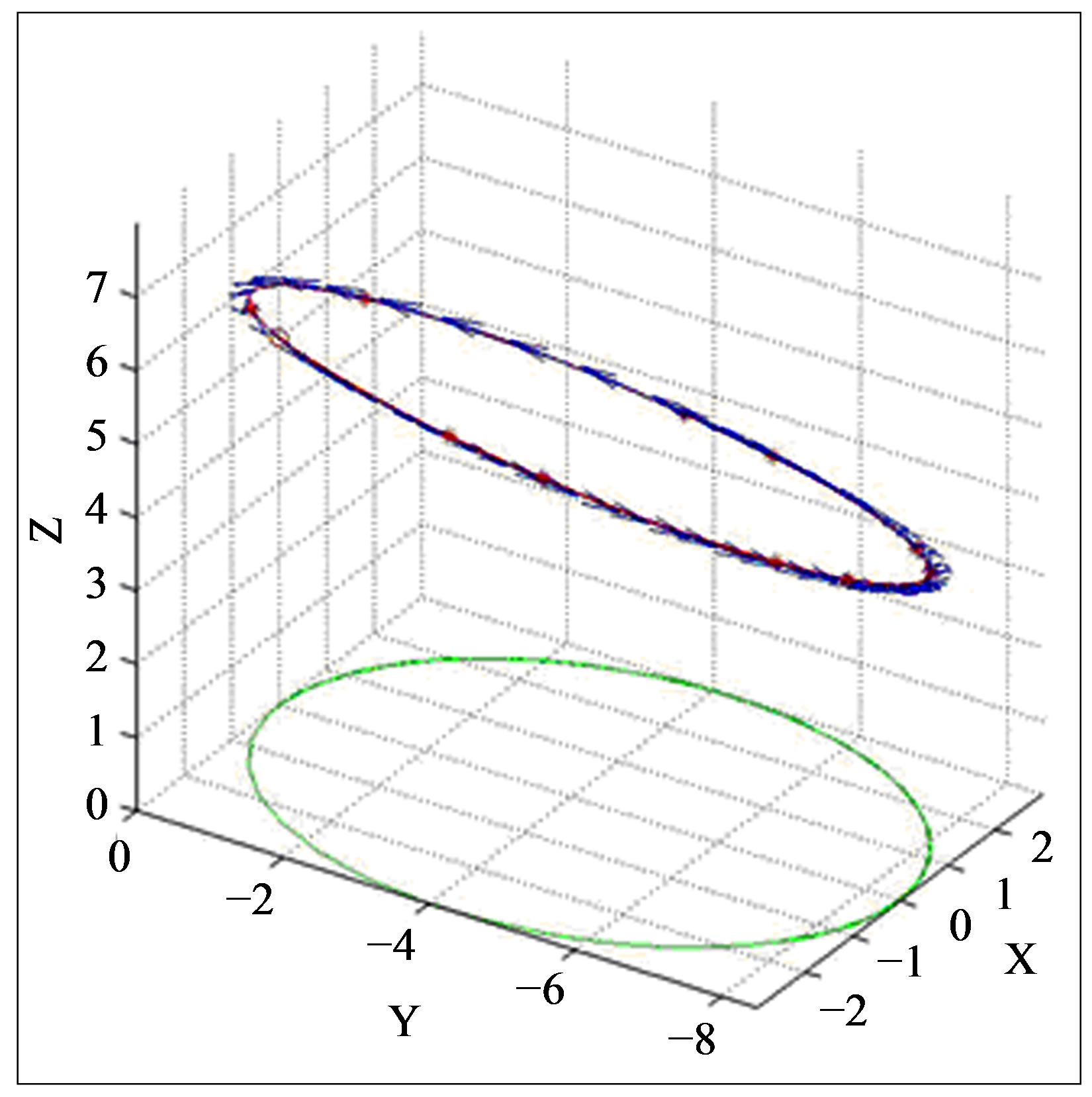
Figure 3. Computer-simulated path of the center of mass of a moving object, which has intrinsic rotation and is simultaneously subject to an external torque non coaxial with its intrinsic angular momentum, when both, the applied momentum and translational velocity of the moving object are constant. For this simulation, the tangential velocity was 5 m/s.
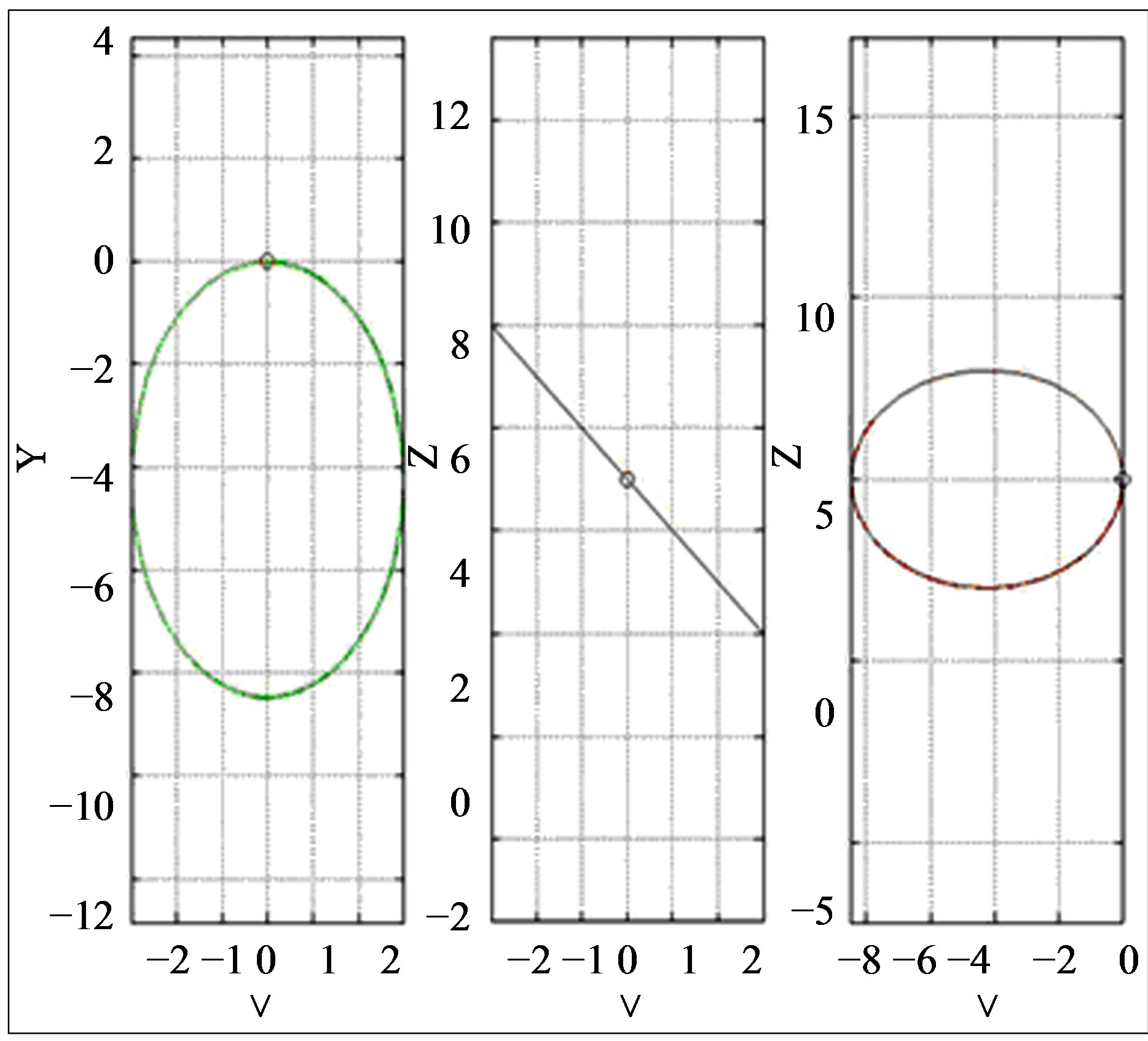
Figure 4. Projection of the generated orbit, of the previous figure, on three reference planes. Conditions of simulation: tangential velocity 5 m/s and constant torque, perpendicular at each moment with the tangential speed vector. It is to be noted that the orbit is flat.
of human knowledge of the universe, I did not find any previous trace of these conclusions, nor did I find any previous historical references when I studied the mechanics of bodies submitted to different non coaxial simultaneous rotations [12].
4.1. Imago Universi
This study of the evolution of human knowledge of the cosmos resulted into the book: Imago Universi, a story of human conception of the cosmos [13]. The text describes the human evolution of the image of the universe (Imago Universi), and how human observation was generated by different and new hypothesis of the celestial dome, and, through time, the development of new mathematical models and new structures based on the logical reasoning to understand the behavior of the universe. It also analyses the evolution of the knowledge of rotational mechanics and its application to celestial mechanics.
The text reminds that the phenomenon of orbitation of the planets around the Sun, simultaneously with its intrinsic rotation around its axis, is not explained by Newtonian mechanics. Newton neither explains the reason for the rings of Saturn nor many systems of flat rings in our solar system like the asteroid belt, the Kuiper belt or the diffused disc.
Therefore, when elaborating this dynamics theory, I intuitively acknowledged its possible application to better comprehend the natural environment and to justify the harmony and structural stability of the universe.
In the last chapter of Imago Universi, the application of the Theory of Dynamic Interactions to astrophysics and specifically to the dynamic of stellar systems and galaxies is included. The treatise has a video of presentation that can be viewed [14].
It should be underlined here that the usual and repeated movements in the universe are mainly accelerated by rotation, except those of free fall. However, the general theories of Relativity of Einstein, the relativity of Galileo-Newton and, in general, also classical mechanics, are based on the assumption of traslational relativity. These theories consider transformations as traslational coordinates and therefore, when describing rotation movement, the transformation of angular (or rotational) coordinates has to be added to the transformations of traslational coordinates. Moreover, the apparent inertial forces that might appear assuming accelerations by rotations are not structured in those theories.
To correct this situation, a revision of those theories including a complete description of the inertial forces can be elaborated by e.g. amplifying the relativity theories of Einstein, or the inclusion of the inertial forces, or even the enunciation of a rotational relativity theory.
However, another alternative could be the development of such a theory of rotational relativity directly from the dynamic analysis of accelerated movement of celestial bodies due to rotations, without including fictitious inertial forces. As such the theory would derive directly from the analysis of the resulting dynamic fields, and the study of its natural coupling, in line with the proposal of the Theory of Dynamic Interactions.
The standard cosmological model has chosen to assume the Newtonian laws conceived for traslation movement. Nonetheless, in this conceptual framework it is necessary to face the observed lack of performance of the Newtonian laws. The contradiction between predictive calculations and the known observations, has forced estimate the existence of other energy and other non-baryonic mass, not observed on Earth. Therefore, such energy and dark matter, non-baryonic and not detected on Earth, appears deductively to justify the failure of compliance with the laws, as the cause of this incoherence.
On the contrary, our text suggests there exists a still wide field of research in relativistic mechanics in relation to these questions and we therefore advocate the need of a profound revision of the structure and limits of classical mechanics, such as the proposal of a theory of rotational relativity, to fully understand the behavior of the Universe.
Imago Universi is a historical narration of the human process of discovery of the universe but also suggests new keys to the understanding of its behavior and comprehends its centuries-old dynamic balance.
4.2. Orbitation and Rotation
As indicated above, bodies that orbit in space rotate around their own axis. According to our analysis, this constant has not been modeled up to date. Our dynamics proposal justifies how bodies with intrinsic rotation and submitted to non-coaxial torques, initiate on the plane, defined by the acting torque and the velocity of initial traslation, a new trajectory which, in case the torque is kept constant, will generate a new path of closed orbit. Therefore, we propose that in the case of dynamics systems in which simultaneous movements of intrinsic rotations and orbitation are observed, the possible existence of dynamic interactions can be inferred, and a mathematical model constituted by the new and simple equation of movement (1) as proposed in our Theory of Dynamic Interactions.
Besides a better understanding of the balance of the universe, allows us to conceive the real dynamics of galaxies and the reason for the plane of the ecliptic or of the rings of Saturn, Figure 5. According to the Theory of Dynamic Interactions, we deduce that the rings can respond to the effect of a constant external torque.
4.3. Dynamic Balance
The Theory of Dynamic Interactions holds that a body with simultaneous traslation and rotation movement, submitted to a new non-coaxial constant torque, will, instead of undergoing acceleration in its rotation as classical mechanics put forward, maintain a constant and apparently immutable dynamic balance. We consider that the theory we put forward, allows a better comprehension of the dynamic behavior of the celestial bodies and its age-old dynamic balance. Besides, we consider that this balance of the universe is not within the parameters of the present laws of classical mechanics.
This Theory of Dynamic Interactions also allows us to answer an initial aporia: establishing and comprehending the physical and mathematical correlation between orbitation and intrinsic rotation and, subsequently, the rational cause for having days and nights on Earth, as in our theory there is a clear correlation between the intrinsic turn of the Earth and its path in its orbit.
That required physical correlation between the intrinsic rotation of the Earth, and the course of its orbit around the Sun, which establishes our theory, is what generates the days and nights on our planet.

Figure 5. It can be observed that the rings of Saturn are present in its equatorial plane (Courtesy of NASA). Moreover, like the rest of these systems, they are developed on a plane, just as is the case with the asteroid belt, the Kuiper belt or the scattered disc. Our proposed theory justifies this behavior.
5. Interpretation of Celestial Mechanics
We believe that the outcomes of the Theory of Dynamic Interactions allow us to raise a new perspective in dynamics, unknown up to date. We have reached to the conclusion that there exists an area of specific scientific knowledge still unstructured in the here defined dynamic assumptions and, specifically, in the analysis of rigid bodies submitted to non-coaxial simultaneous rotations.
We strongly suggest the study of a model of the universe in which the forces applied to rotating bodies do not always create accelerations in proportion to the mass which, with a constant force, would imply velocities growing infinitely, as occurs in classical mechanics. Instead, the momenta of the forces generate a dynamic balance by transferring linear velocities to orbital velocities, and transform the rectilinear trajectories into curvilinear and orbital trajectories. We propose the association of dynamic effects to the velocity whereas in classical mechanics, and according to Newton’s second law, the dynamic causes are linked to the changes of speed.
The observation of the answer of mass to successive actions of modification of the angular momentum of the bodies in multiple assumptions and examples shows repeatedly the existing contradiction between classical rotational mechanics and the real behavior of nature. We propose a new conceptual structure to explore the dynamics of celestial bodies in a frame of accelerations and, more specifically, we suggest the application of celestial mechanics of rigid bodies submitted to multiple non coaxial rotations.
Regarding this approach, we wonder if this is not the true reality of the human being observing from planet Earth. For the Earth is constantly in intrinsic rotation, while orbiting around the Sun, which in turn has also intrinsic rotation, since it orbits around the axis of the galaxy, which also rotates.
We are of the opinion that it is not possible to apply a traslational dynamics in such a reality of simultaneous rotations to justify the behavior of celestial bodies.
Science tries to interpret the universe, building up a unifying theory in which even its initial conditions are consequences of its own laws of physics. We, on the other hand, suggest that by combining the general relativity with our dynamics proposal [15], it would be possible to define a model of cosmos which would possibly be more in accordance with the observable universe.
We are facing a fascinating collective work, an enormous intellectual and research effort to try to reach a better vision of the universe and to dispose of a real scientific cosmology.
6. Conclusions
Through a historical overview of the science of the universe, we have recovered a forgotten controversy of mechanics and we believe to have started the study of a new field of knowledge. We should be aware that the Newtonian mechanics of inertial systems is a specific discipline of the knowledge of nature, but it is constrained, and therefore it is necessary to explore new areas such as the dynamics of non-inertial systems.
We would like to accurately interpret the real behavior of bodies submitted to multiple non-coaxial rotations and incorporate the inertial phenomena to the structure of the knowledge of physics. We understand that regarding these questions, there is still a wide field of research in both, relativistic and non-relativistic mechanics that cannot be considered as fully resolved and tested in present modern physics.
After analyzing the reactions and inertial fields that can not be explained by classical mechanics, the Theory of Dynamic Interactions is proposed to better interpret celestial dynamics.
As indicated above, we have carried out the experimental test [16] of the inferred hypotheses starting from our initial conjectures and, moreover, third parties have also conducted experimental tests confirming our hypotheses [3]. These experimental tests have been recorded and can be visualized on different websites [2,5, 15].
Precisely, Penrose in his book “The Road to Reality: A Complete Guide to the Laws of the Universe” [17] intended to offer a guide to determine the laws of the universe and included different works and studies where his ideas had been used. The text ends up with the following paragraph: Perhaps what we mainly need is some subtle change in perspective—something that we all have missed… We can ask ourselves if our proposal could answer this question of perspective posed by Penrose, in a satisfying way.