Emergence of the Macroscopic Quantum Superposition State in Microtubules ()
1. Introduction
MTs are important for components and function units in cytoskeletons, as well as cellular organization and information processing [1-6]. MTs are ubiquitous in the entire biology, especially enriched in brain tissue [7]. From X-ray crystallography [8], one already knows that a MT is a hollow cylindrical tube about 25 nm outer diameter and 14 nm inner diameter. The interior of the cylinder is likely to be filled with ordered water which implies the existence of electric dipoles and an electric field. The MT wall is an assembly of 13 protofilaments, each of which is a series of subunit proteins known as tubulin dimers. Measurements by electron crystallography [9] have further demonstrated the structure of the tubulin subunit. Each tubulin subunit is a peanut-shaped dipolar, 8 nm dimer consisting of alpha and beta 4 nm monomers, called the 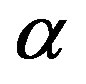 -tubulin and
-tubulin and  -tubulin, respectively. The electric dipolar character of the
-tubulin, respectively. The electric dipolar character of the 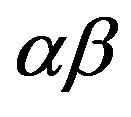 -tubulin dimer originates from 18 Ca ions bound within each
-tubulin dimer originates from 18 Ca ions bound within each  -monomer and an equal number of unpaired electrons localized near the neighbouring
-monomer and an equal number of unpaired electrons localized near the neighbouring 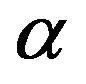 -monomer (Figure 1). Many physicists pay attention to the notion that MTs process information and posses quantum computation [1-6,10-15]. Hameroff considered that Orch OR (Orchestrated objective reduction) is a viable approach toward understanding how the brain produces consciousness [12,15]. Orch OR is based on quantum computation in MTs within dendrites in cortex and other regions linked by dendriticdendritic gap junctions (“dendritic webs”) acting as laterally connected input layers of the brain’s neurocomputational architecture. Dendritic cytoplasmic MTs are isolated from their classical/non-quantum environment in quantum state phases of superpositioned entanglement. Orch OR quantum mechanisms provide the most credible explanations of mental phenomena. In 1994, M. Jibu presented a theoretical prediction of the occurrence in biological media of the phenomena which they term “superradiance’ and “self-induced transparency” [16]. Interac-
-monomer (Figure 1). Many physicists pay attention to the notion that MTs process information and posses quantum computation [1-6,10-15]. Hameroff considered that Orch OR (Orchestrated objective reduction) is a viable approach toward understanding how the brain produces consciousness [12,15]. Orch OR is based on quantum computation in MTs within dendrites in cortex and other regions linked by dendriticdendritic gap junctions (“dendritic webs”) acting as laterally connected input layers of the brain’s neurocomputational architecture. Dendritic cytoplasmic MTs are isolated from their classical/non-quantum environment in quantum state phases of superpositioned entanglement. Orch OR quantum mechanisms provide the most credible explanations of mental phenomena. In 1994, M. Jibu presented a theoretical prediction of the occurrence in biological media of the phenomena which they term “superradiance’ and “self-induced transparency” [16]. Interac-
tions between the electric dipole field of water molecules confined within the hollow core of MTs and the quantized electromagnetic radiation field are considered, and MTs are theorized to play the roles of non-linear coherent optical devices. “Laser-like”, long-range coherent quantum phenomena may occur biologically within cytoskeletal MTs. Chen ying et al studied water molecules in MTs [17]. The liquid water is a very complicated system and it is well known that water molecules possess a considerable electronic dipole [18]. In this paper, we study the interaction between the electronic dipole field of water molecules in MTs and the quantized electromagnetic radiation field. The incoherent, thermal and disordered molecular movement can excite the water molecules from ground state to excited state and transfer into the collective coherent radiation. The collective coherent radiation can be treated as the coherent state. Water is a Kerr medium which contains non-linear effect. When propagating in it, the coherent state we concerned in this paper can evolve into quantum superposition states.
2. The Physical Model
2.1. The Collective Coherent Radiation of Water in MTs
Taking water molecules as rigid rotor, considering the rotation of the water molecules and the interaction between the electronic dipole field of water molecules and the quantized electromagnetic radiation field, the liquid water in a volume V is defined by the following Hamiltonian:
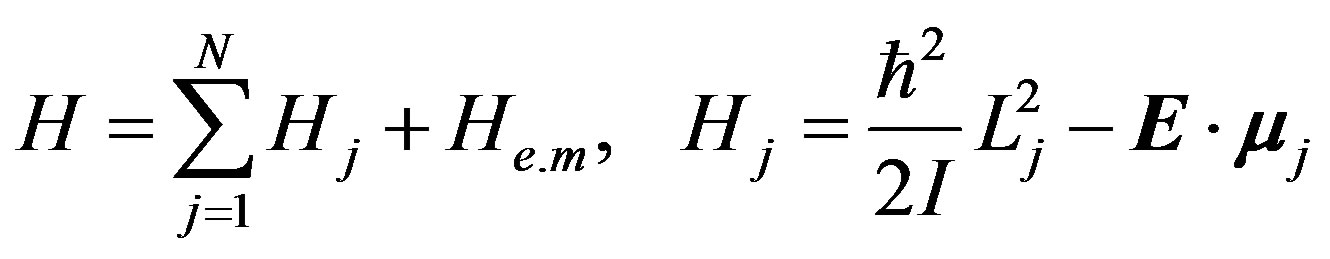 (1)
(1)
where the sum runs over the N molecules of the volume V, and Lj its the total angular momentum of the single molecule, I its momentum of inertia, and μj its electric dipole vector. 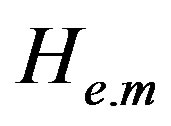 is the Hamiltonian of electromagnetic field.
is the Hamiltonian of electromagnetic field.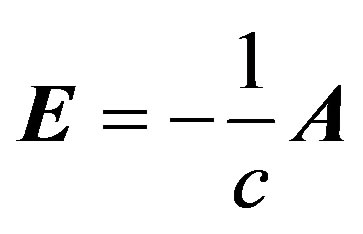 , A denotes electromagnetic field in the radiation gauge. By standard quantum-field-theory methods it is straightforward to write down the Lagrange function that describes the dynamics of the system in natural units
, A denotes electromagnetic field in the radiation gauge. By standard quantum-field-theory methods it is straightforward to write down the Lagrange function that describes the dynamics of the system in natural units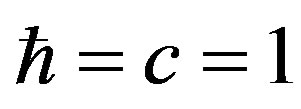 :
:
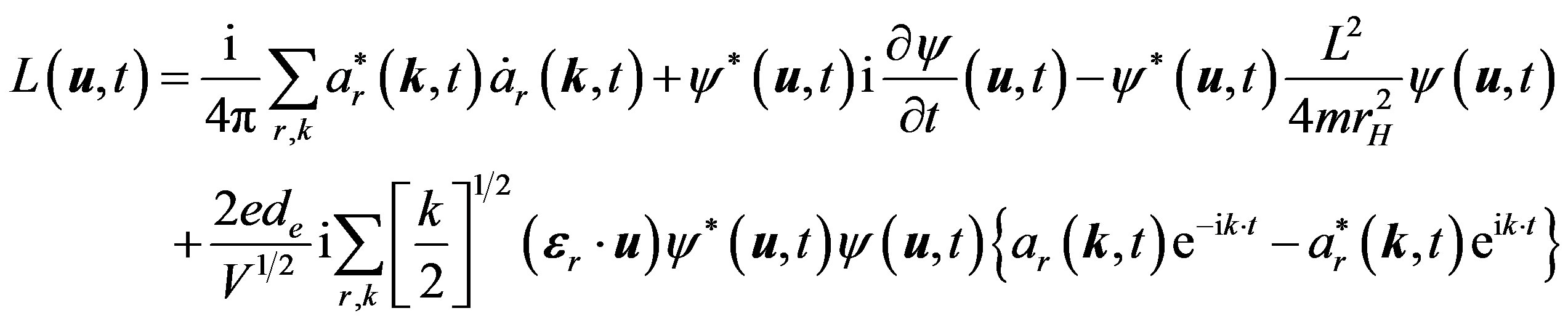 (2)
(2)
The Noether theorem leads to the following conserved quantity:
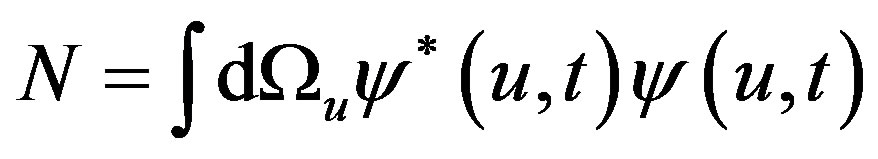 (3)
(3)
Using the relevance of the following rescalings:
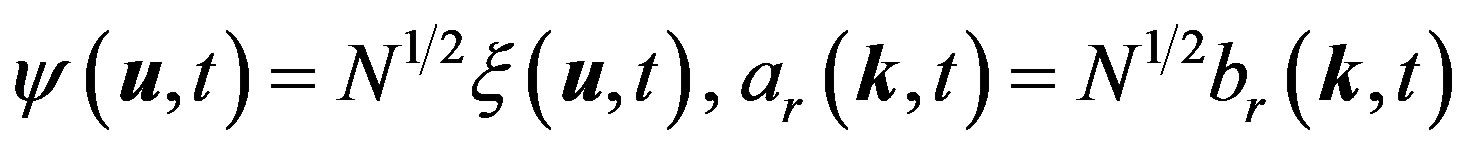 (4)
(4)
Based on Schwinger quantum field theory,
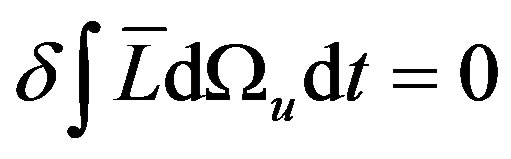 , the variational problem yields the following Euler-Lagrange equations:
, the variational problem yields the following Euler-Lagrange equations:
Taking the molecular as two energy states system approximately, we can obtain that the region of the quantized radiation field is 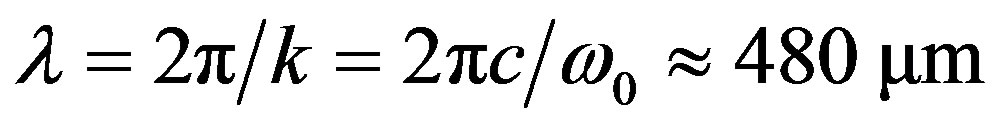 and the time scale is
and the time scale is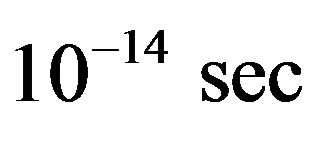 .
.
2.2. Kerr Effect of Water in MTs
Water is a Kerr medium which contains non-linear effect. In our system, the non-linear part induced by Kerr effect should be added to the Hamiltonian
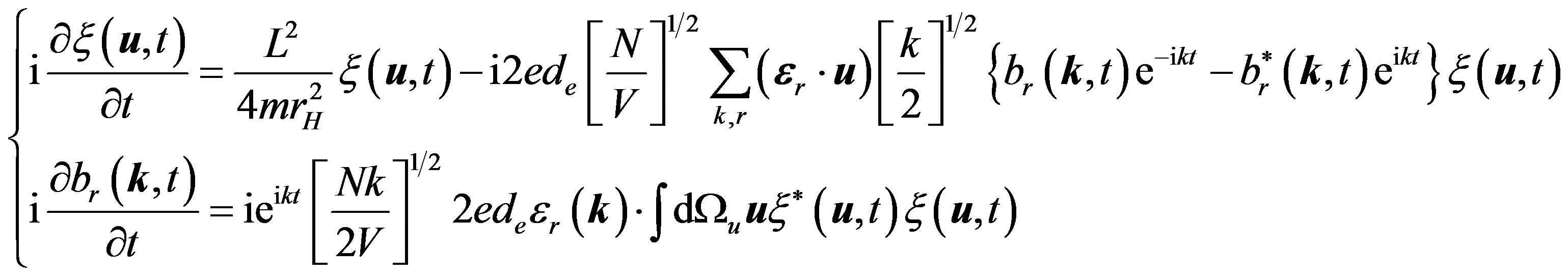 (5)
(5)
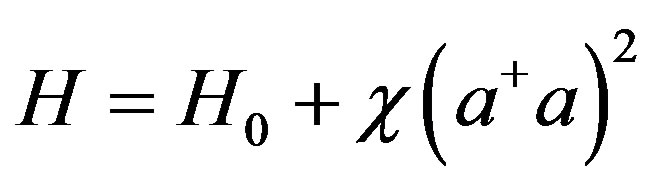 (6)
(6)
where the coupling coefficient 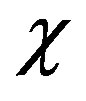 denotes Kerr effect strength of the medium. The relation between
denotes Kerr effect strength of the medium. The relation between 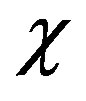 and the third-order non-linear item
and the third-order non-linear item 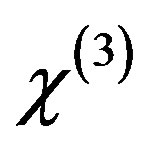 is
is
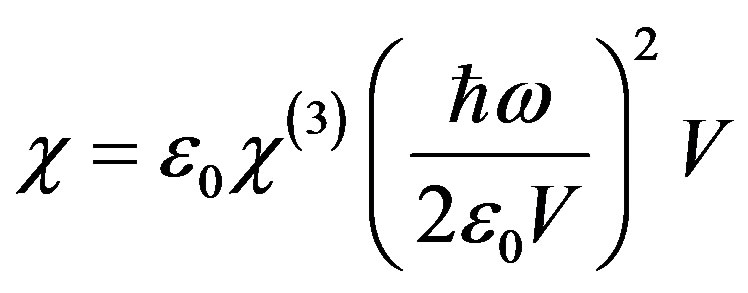
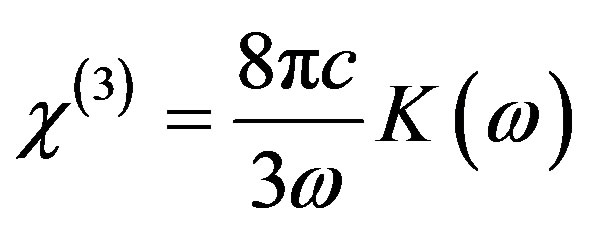 (7)
(7)
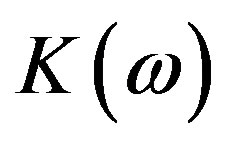 is Kerr constant, the values of
is Kerr constant, the values of 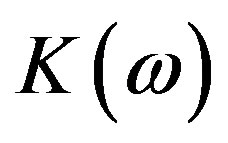 depend on the medium and are about
depend on the medium and are about 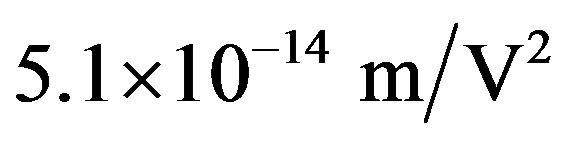 for water. For MTs, in the region of the quantized radiation field
for water. For MTs, in the region of the quantized radiation field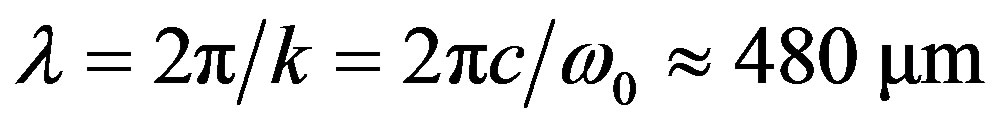 , we can calculate
, we can calculate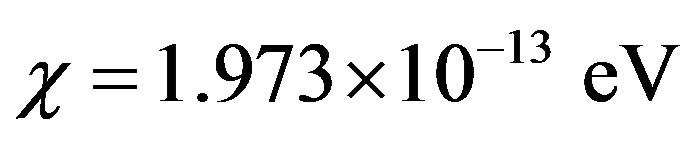 .
.
3. Generation of the Macroscopic Quantum Superposition State in MTs
There maybe exists collective coherent radiation of water in MTs. A well-known example of a coherent field is one which is in an eigenstate 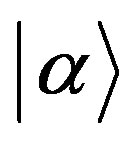 for all the modes of the field. So in MTs the photon emitted from collective coherent radiation can be described by such an eigenstate
for all the modes of the field. So in MTs the photon emitted from collective coherent radiation can be described by such an eigenstate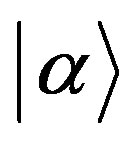 . The initial coherent state may be expressed as a superposition of number states as follows:
. The initial coherent state may be expressed as a superposition of number states as follows:
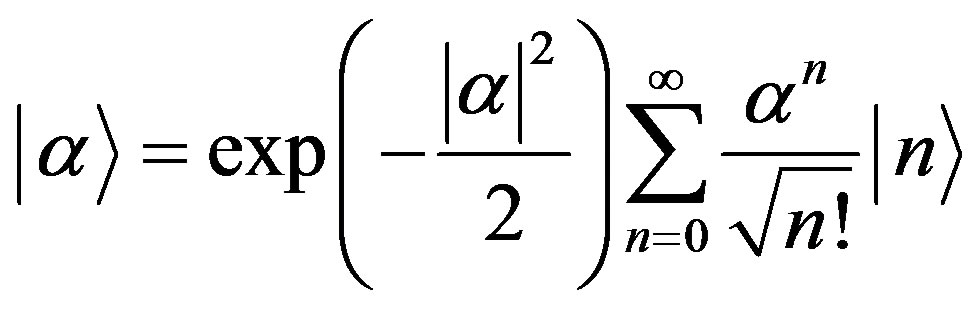 (8)
(8)
When the state transfers in the MTs, it will be interacted by the system Hamiltonian
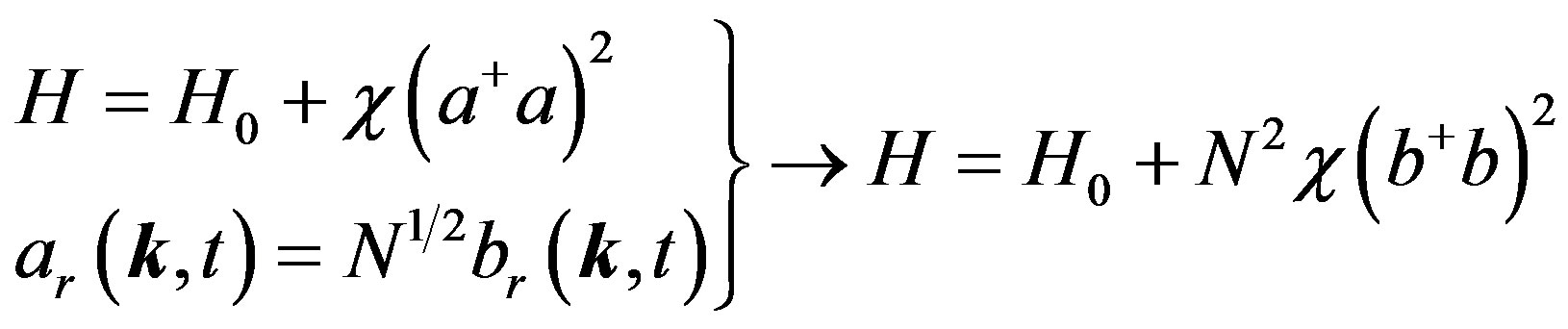 (9)
(9)
and the time development of the coherent state is
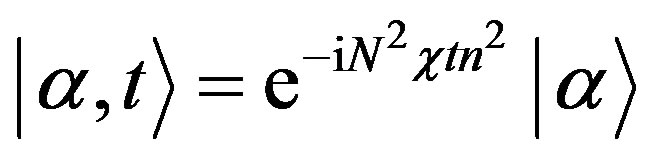 (10)
(10)
From Equations (8) and (10), one can find
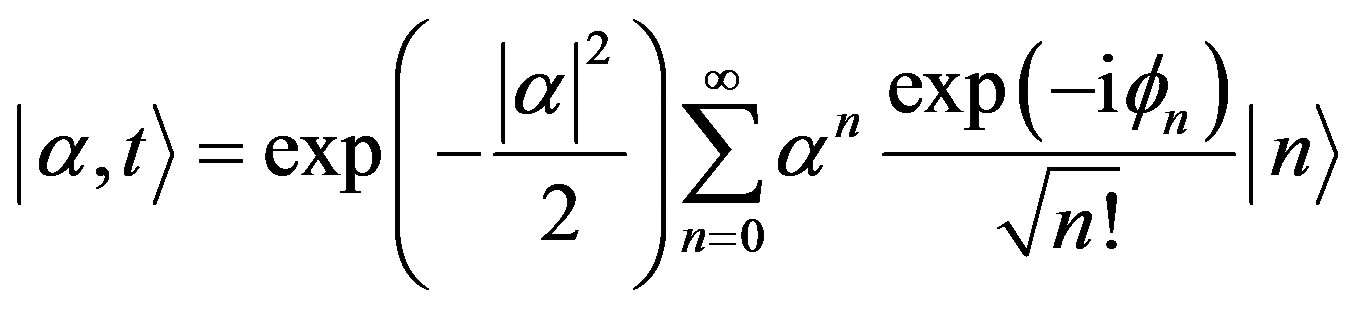 (11)
(11)
where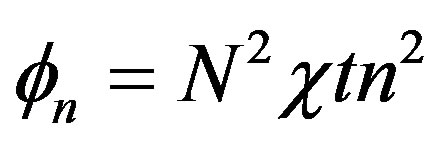 .
.
When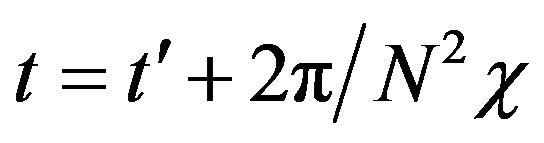 , one can obtain:
, one can obtain:
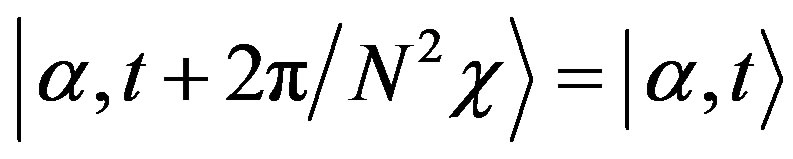 (12)
(12)
Particularly interesting would be at the time
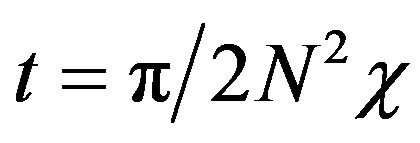 , the coherent state becomes:
, the coherent state becomes:
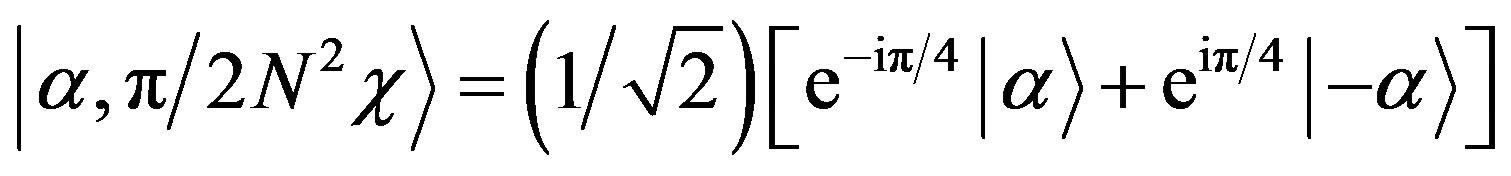 (13)
(13)
which is called the quantum superposition state of a macroscopic system.
We assume that the equilibrium distribution is a Boltzmann distribution for the all the water molecules in excited state.
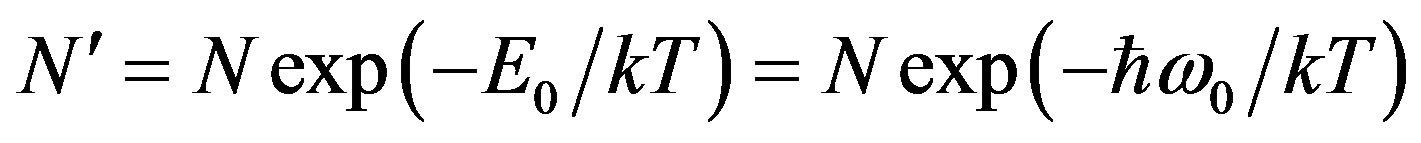 (14)
(14)
For MTs with different length, we calculated the relevant parameters including the evolving time t and propagating distance d to form the quantum superposition state. In Table 1, l is the microtubule length, N is water molecule number and 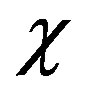 denotes the coupling coefficient.
denotes the coupling coefficient.
4. Discussion
Many scientists are interested in the human receptory organs since they are the places where manifestations of quantum effects from the standpoint of their sensitivity and response have been reported so far. At the cell scale, human brain has quantum (molecular) receptors of the outside fields. These receptors absorb electromagnetic radiation at the level of tens to thousands of quanta per mode as well as phonons in the same amount. MTs found throughout the neuron are the major cytoskeletonal element in dendrites. It will be of interest to obtain further insight into its “quantum computer” aspects.
From Table 1, we can see it is very easy to generate the macroscopic quantum superposition states in long MTs. When the length of MTs less than 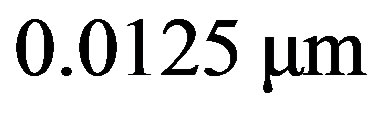 (12.5 nm), there are not enough region to form he macroscopic quantum superposition states. Fortunately, the
(12.5 nm), there are not enough region to form he macroscopic quantum superposition states. Fortunately, the
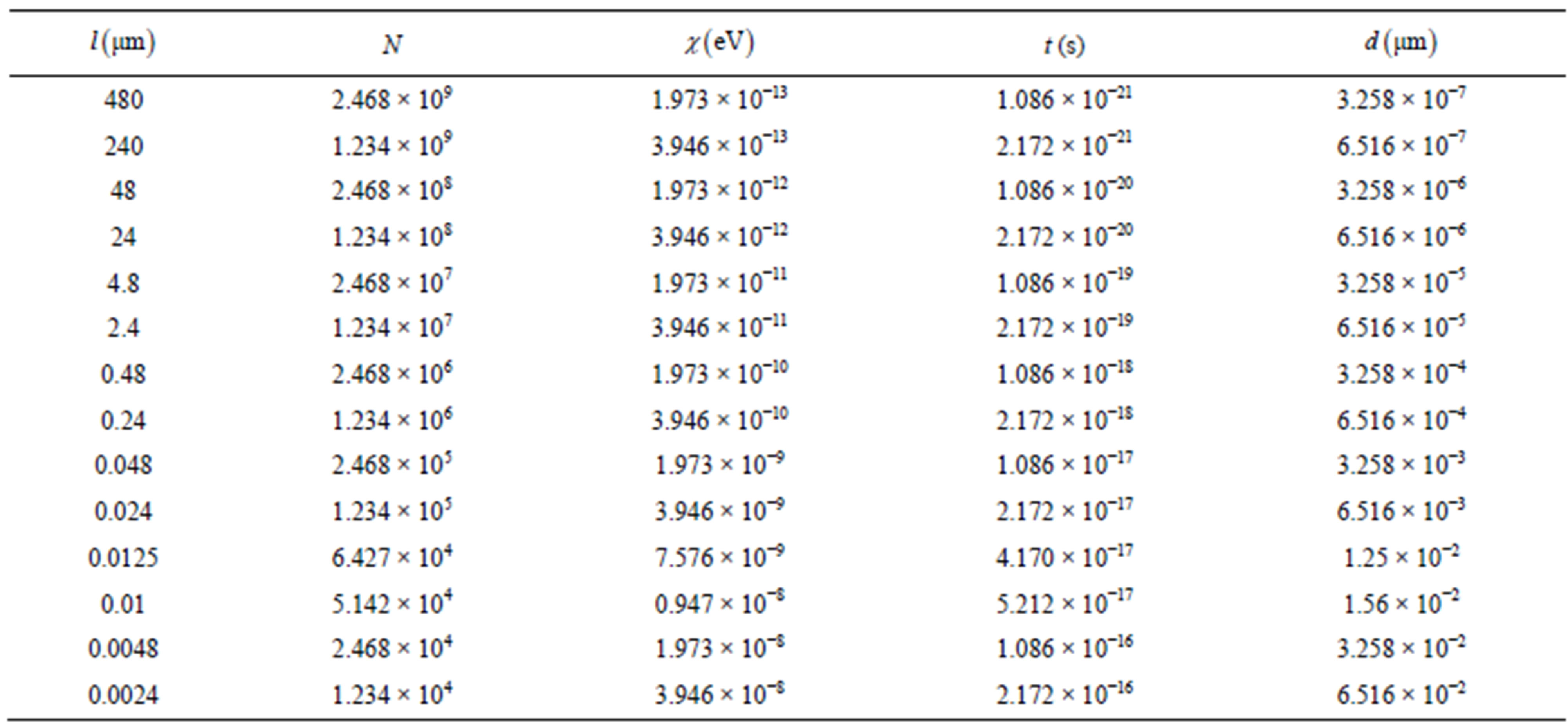
Table 1. Corresponding parameters for microtubule with different length.
length of most MTs are larger than 100 nm and some can reach centimeter. Therefore the macroscopic quantum superposition states are ubiquitous in MTs. Quantum coherence function a central role in transmission of information. But it is frangible. Yet the macroscopic quantum superposition states possess the characteristic of quantum coherence and classic characteristic of macroscopic objects, and it is stable. As a result, one can envisage the possibility that the coherent interaction between the water electric dipoles and the radiation field fulfills the very important task of generating ordered structures in macroscopic domains and the coherent state evolves into the macroscopic quantum superposition state which could then have a fundamental role in the information processing. Of course much more work is need in this direction.
NOTES
#Corresponding author.