A Self-Adaptive Parallel Encryption Algorithm Based on Discrete 2D-Logistic Map ()
2. Self-Adaptive Parallel Encryption Algorithm Based on Discrete 2D-Logistic Map
2.1. Discrete 2D-Logistic Map
With the development of technology, more and more fields are related to discrete-time multivariable system which mathematical model is deviation equation. Those discrete-time multivariable systems are called space discrete dynamic system [15], that is, 2D-discrete dynamic system denoted as
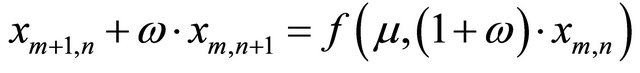(1)
where f() is a nonlinear function, also known as forcing function. Ω Î (–∞,+∞) is a real number. μ > 0 is a constant. m, n and xm,n are states of space system. In fact, difference Equation (1) is the discrete form of one-dimensional convection Equation 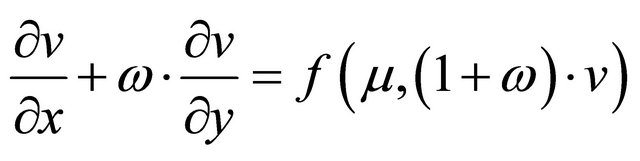(2).
(2)
Particularly, when n = n0, ω = 0, Equation (2) is denoted as
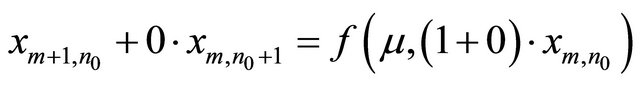(3)
Because n is constant n0, Equation (3) can be expressed as follows:
(4)
Therefore, 1D-discrete dynamic system Equation (4) is a special case of 2D-discrete dynamic system Equation (1). When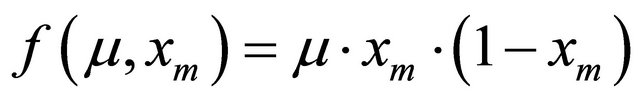
, Equation (4) is expressed as
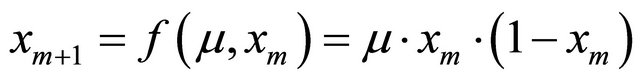(5)
This is classic 1D-Logistic map. When
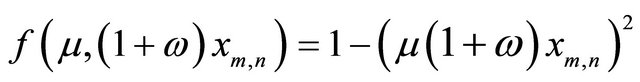2D-discrete dynamic system is denoted as:
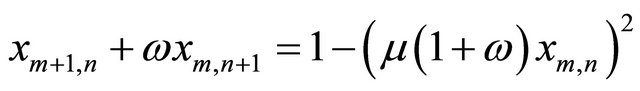(6)
Study shows that the system Equation (6) is chaotic state with 2 > μ >= 1.55 and ω Î (–1,1), and has two iteration variables which is known as 2D-Logistic map.
There are two control parameters in space chaotic system. Space chaotic orbits are extremely sensitive to the change of control parameters. When μ = 1.96, ω = –0.05, the chaotic behavior of space chaotic system is described as Figure 1.
2.2. Demands of Parallel Encryption Algorithm
Parallel encryption algorithm refers to encrypting one image simultaneously by two or more processing elements (PE for short). Each PE has its separate memory space and computing resource. One superior parallel encryption mode must meet the following demands [13]:
1) Good diffusion effect Small changes in plain text or key have a big influence on cipher text is called diffusion which is known as avalanche effect. Generally CBC mode is used to realize fully diffusing in existing encryption algorithms. However, the application of CBC makes algorithm steps become serial mode. Therefore, the encryption algorithm is not only parallel operation but also can achieve fully diffusing.
2) Load balance of computing quantity Computing time depends on the PE with the longest running time. Therefore, the calculated quantity of every PE should be equal for a good parallel encryption algorithm.
3) Critical section management Two or more PE may read and write one memory area in parallel operation, and this memory area is called
Figure 1. Chaotic behavior of space chaotic system.
critical section. Therefore, one good parallel algorithm should avoid this situation.
2.3. Inter-Block Encryption Algorithm
It is assumed that one original image of size 
is encrypted by r processing elements
, and meets the divisibility of r dividing M. The encryption process is as follows:
Step 1. Key generation. The binary sequence 
is generated according to user key, where the binary values 0 and 1 represent two distribution forms of processing elements, and the number of binary sequence is cycle number.
Step 2. Image segmentation. The plain-text matrix is divided into r blocks. If bn = 0, PEi encrypts the pixels of matrix block which is from the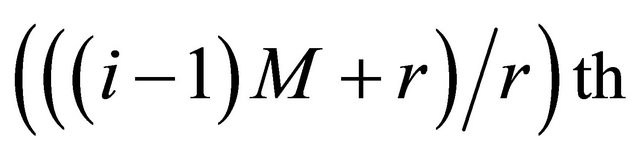 
row to the 
row of plain-text matrix. If bn = 1, PEi encrypts the pixels of matrix block which is from the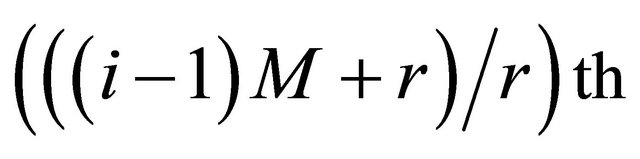 
column to the 
column of plain-text matrix, where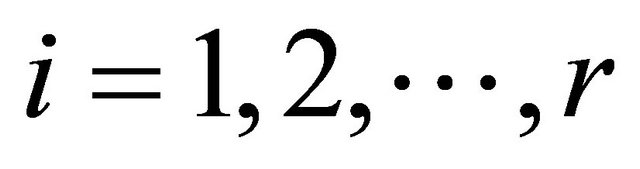
.
Step 3. Each matrix block is scrambled and mixed by one processing element.
Step 4. Go to Step 1 until the end of the loop.
2.4. Encryption Algorithm in Block
Assumed that the original image is P, and the pixel matrix is denoted as
(7)
where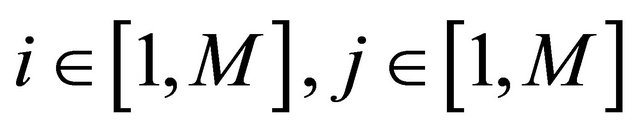
. A numerical matrix K of size 
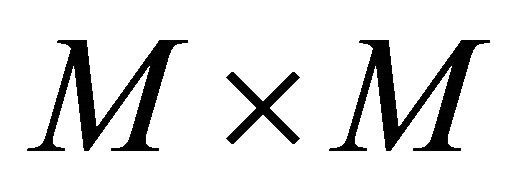is produced according to 2D-discrete dynamical system, which is represented in Equation 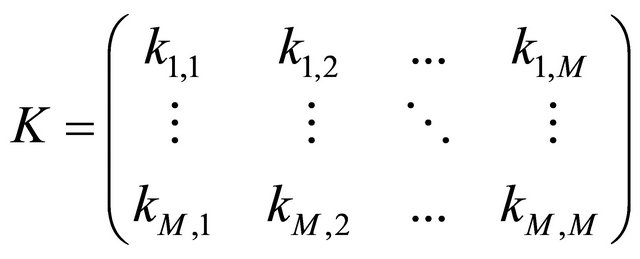(8).
(8)
where
. In the following, the steps of the proposed algorithm are described in detail.
Step 1. The distribution form of processing elements is defined according to binary sequences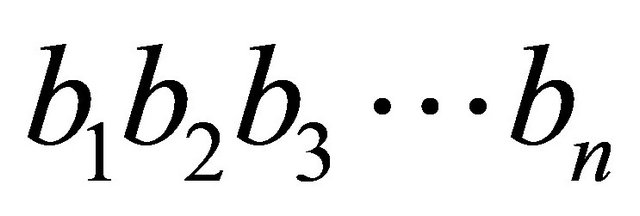
.
When bn = 0, the numerical matrix K is divided into r blocks in row direction. The ith numerical matrix block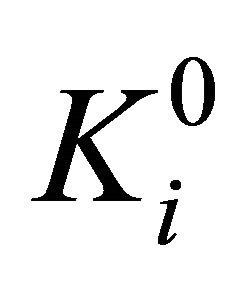 
is denoted as
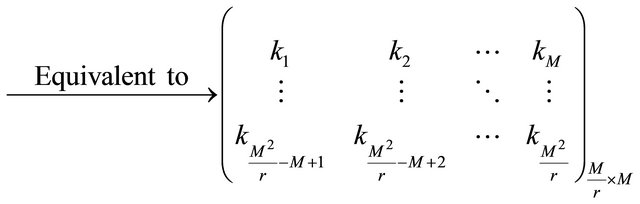
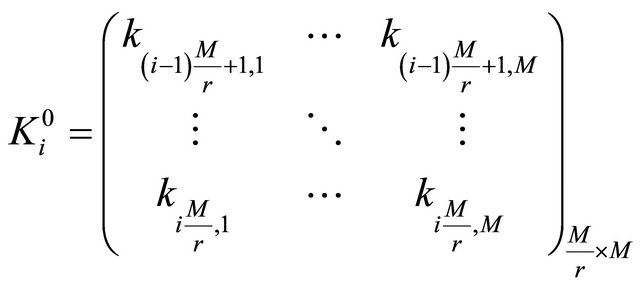(9)
Then the numerical matrix block 
is transformed into ergodic matrix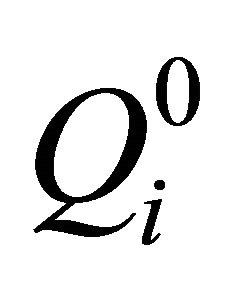 
in Equation 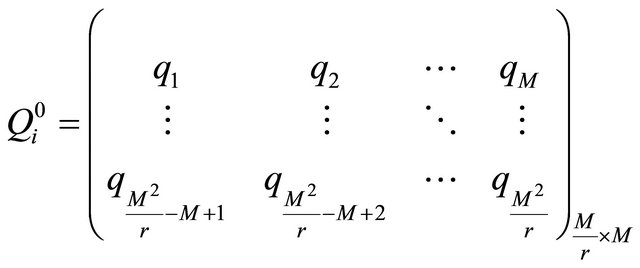(10).
(10)
where
.
When bn = 1, the numerical matrix K is divided into r blocks in column direction. The ith numerical matrix block 
is denoted as
(11)
Then the numerical matrix block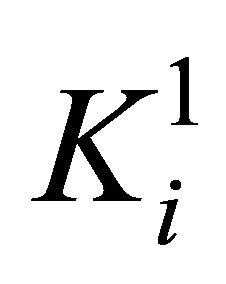 
is converted into ergodic matrix 
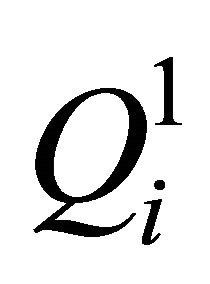in Equation 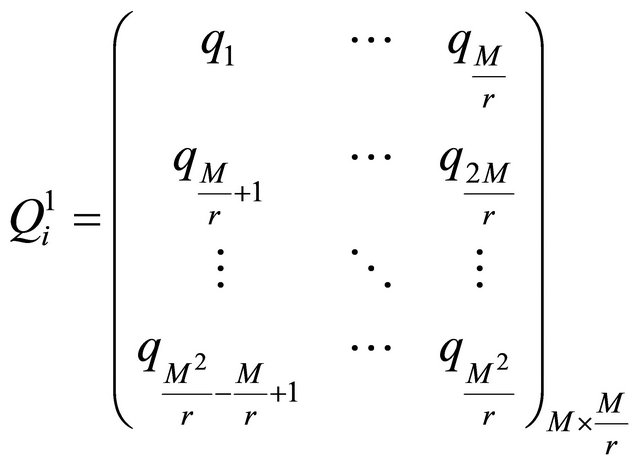(12).
(12)
where
.
Step 2. Position scrambling. We assume that the ith matrix block Pi is scrambled according to ergodic matrix in PEi.
If bn = 0, the ith matrix block 
is scrambled according to ergodic matrix
, after scrambling the matrix is denoted as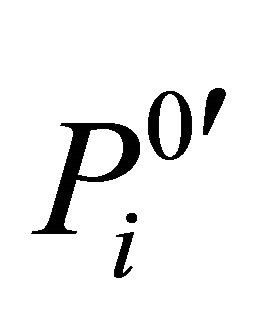 
in Equation (13).
(13)
If
, the ith matrix block 
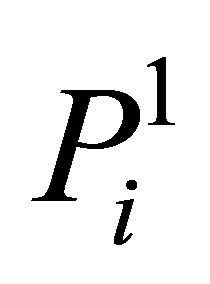is scrambled according to ergodic matrix
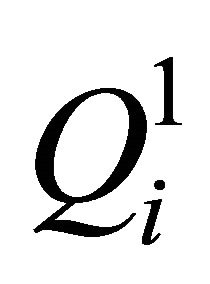, and after scrambling the matrix is denoted as 
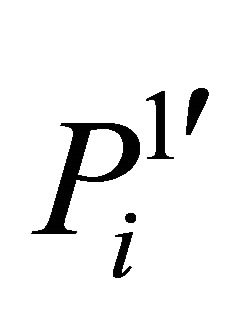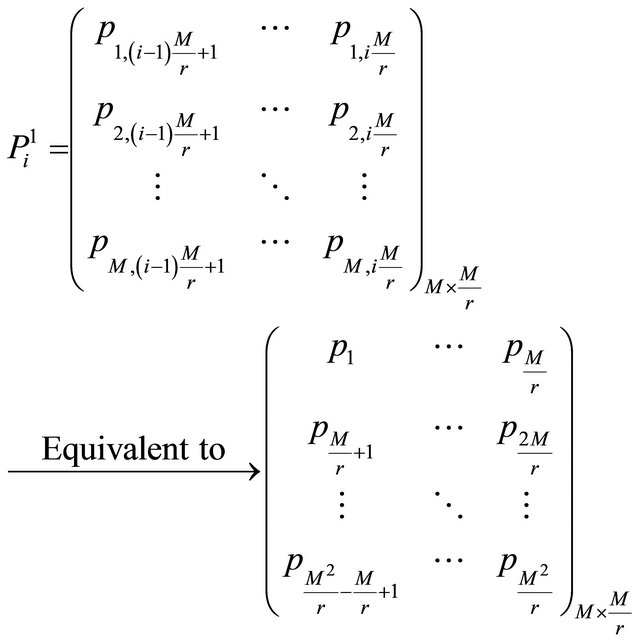
in Equation (14).
(14)
Step 3. Image scrambling can destroy correlation between two adjacent pixels, but it cannot change pixel value thus the histogram is the same with original image. Therefore, the scrambled image should be further encrypted. For example, to encrypt the ith scrambled matrix block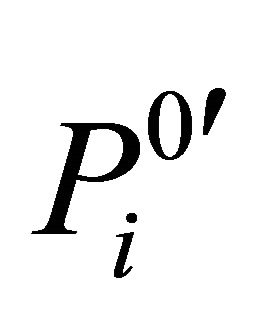 
with bn = 0, and the result is denoted as 
in Equation 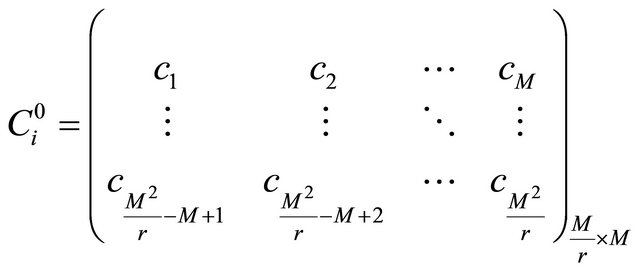(15).
(15)
where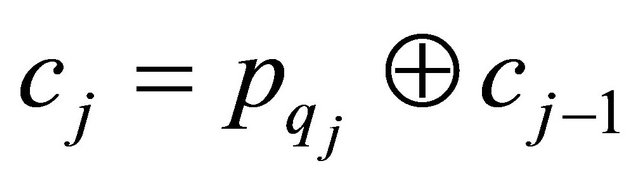 
Go to step 1 until the end of the loop. The detailed encryption diagram is described in Figure 2.
When n = 1, the pixel mixing based on chaining structure can make a small change of one pixel have effect on other pixels in the same block. And when n = 2, the influence can spread into whole image, which meet the demands of parallel encryption algorithms. In addition, the data volume is exactly same for every processing element which can realize load balance. Finally, there is no problem of critical section.
3. Theoretical Analysis and Experimental Simulation
Experimental analysis of the proposed algorithm in this letter has been done. To estimate the performance of the proposed scheme, we carry out a series of experiments. The experimental simulation is all implemented using Matlab8.0 running on a personal computer with i7 – 3770 s 2.8 GHz*4 processor. The parameter is selected as m = 1.96, ω = –0.05.
3.1. Statistical Analysis
The distribution of cipher image is very important because it has to hide the redundancy of original image and should not leak any information about original image or any relation between encrypted image and original image. In statistical simulation, the parameters are selected as b1 = 0, b1 = 1 and b1b2 = 10 respectively. The simulation results are described in Figure 3. As can be seen form Figure 3, if n = 1, the proposed encryption in the paper can hide the redundancy of plain image completely, i.e., it can resist statistical attack effectively.
3.2. Differential Analysis
We know that two main cryptographic properties of a good cipher are confusion and diffusion. Confusion means to complicate the dependence of the statistics of cipher image on the statistics of plain image. Diffusion means to spread out the influence of a single plain image symbol over many cipher-image symbols so as to hide the statistical structure of plain image. Differential attack can be avoided effectively through confusion and diffusion. In order to illustrate the performance of resistance on differential attack directly, we change the pixel value
of Figure 3(a) from 113 to 116 in the position (69,98) to illuminate the confusion and diffusion of Mirzaei’s scheme and our proposed scheme. Some experiments are performed to study confusion and diffusion properties in Figure 4, which there is only a tiny difference in plainimage sequences, and then the difference values of cipher-image sequences are obtained correspondingly. For Mirzaei’s algorithm in Figure 4(a), we observe that if there is only a tiny difference in plain image, and there is only some difference in the second block of cipher image correspondingly. However, for our proposed scheme (n = 1) in Figure 4(b), a tiny difference in plain image results in all the other cipher image change in the third block. And the parameter n = 2 in Figure 4(c), all the other cipher text will be influenced accordingly. Therefore, the diffusion and confusion properties of the proposed scheme are confirmed with n = 2.
In the following, we illustrate the performance of resistance on differential attack numerically. The number of pixels change rate (NPCR for short) and the unified average change intensity (UACI for short) are the significant measure of resistance on differential attack. NPCR and UACI denote the number of pixels change and the unified average change intensity in cipher image respectively, while we change one pixel value in the plain image randomly. Assume that there are two cipher images (
,
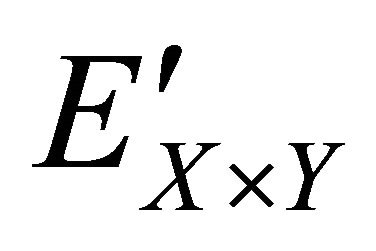) whose plain images only have one different pixel. The pixels in position 
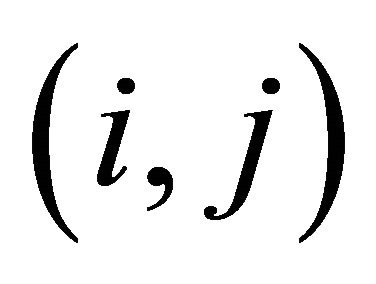of these two cipher images are denoted as 
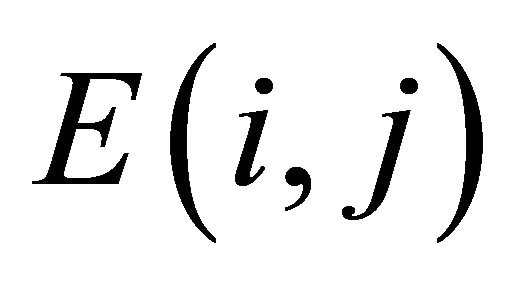and
, respectively. Then one matrix D is defined with the same size of
, and we assume that if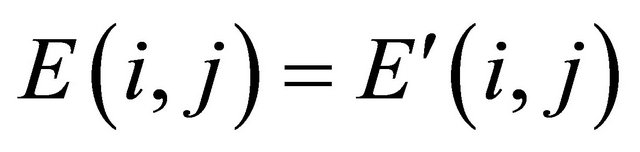
, then
, otherwise,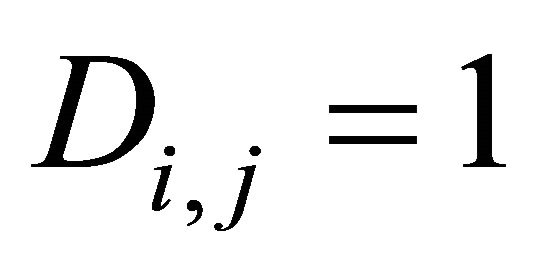
. Therefore, NPCR and UACI can be represented as
(16)
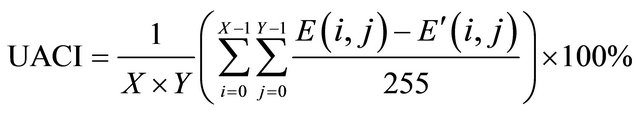(17)
We change the pixel value of Figure 3(a) from 81 to 85 in the position (169,236), and then based on Equation (16) and (17) with n = 2, NPCR and UACI can be calculated to be 99.63% and 31.26%, respectively. Therefore, one pixel change in plain image can lead to completely change of cipher image. We can draw conclusion that the proposed encryption algorithm can resist differential attack effectively.
3.3. Key Sensitivity Test
An encryption scheme has to be key-sensitive, meaning that a tiny change in keys will cause decryption failure completely. The key sensitivity test is performed in detail according to the following steps:
• Figure 3(a) is encrypted with the test key m = 1.96, ω = –0.05, respectively. And its corresponding decrypted image with the correct key is presented in Figure 5(a).
• Then, the corresponding decrypted image with m = 1.96001 is presented in Figure 5(b).
• Again, when one pixel in PE3 is changed, the corresponding decrypted image with the correct key is presented in Figure 5(c), while b1 is chosen as “1”.
Finally, when one pixel in PE3 is changed, the corresponding decrypted image with the correct key is presented in Figure 5(d), while b1b2 are chosen as “10”, respectively.
Based on the simulation mentioned above, we can draw a conclusion that if there is a tiny change in the key explained before, we can obtain a completely different image from the original image. And if there is a tiny change in the plain image, the decrypted image is completely different form the original image, while b1b2 are chosen as “10” respectively. Those simulation results show high key-sensitivity and plain-text sensitivity of the
(a) (b) (c)
Figure 4. Difference in cipher text changing the pixel value of Figure 3(a) from 113 to 116 in the position (69,98). (a) Mirzaei’s. (b) Ours: n = 1. (c) Ours: n >= 2.
proposed algorithm.
3.4. Analysis of Information Entropy
Entropy H(x) was introduced by Shannon in 1949 firstly and can be obtained through the following formula:
(18)
where n is the number of gray scale levels in an image,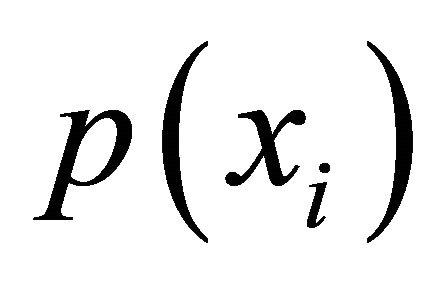 
is the occurrence probability of gray scale in the image and meets the following formula:
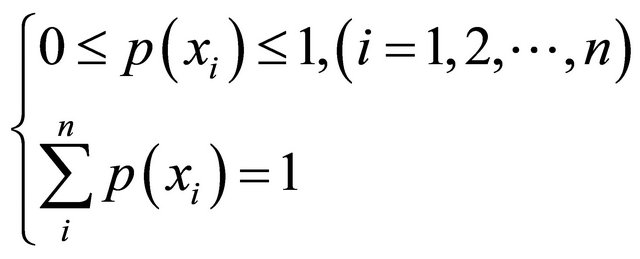(19)
The entropy value will be 8 for images that are produced totally randomly. The closer the entropy of an algorithm is 8, the less predictable, and thus the more secure the scheme. The cipher-image entropy values have been measured using six plain images in USC-SIPI data base and the results are shown in Table 1.
3.5. Analysis of Correlation of Two Adjacent Pixels
Each pixel in the digital image is not independent of other pixels, but has significant correlation. One of purpose for an encryption algorithm is to decrease correlation between adjacent pixels and realize zero co-correlation properties. To show correlation between adjacent pixels in encrypted images, we take Figure 4(a) for example to analyze correlation between two vertically adjacent pixels, two horizontally adjacent pixels, and two diagonally adjacent pixels, respectively.
Table 1. The entropy of original gray scale image and its corresponding encrypted ones by the proposed algorithm.
(a)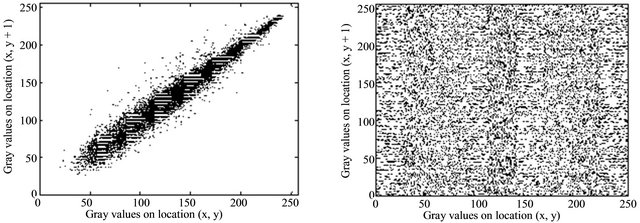
(b)
(c)
Figure 6. Correlation of two adjacent pixels. (a) The distribution of vertically adjacent pixels in Figure 3(a). (b) The distribution of vertically adjacent pixels in Figure 3(b). (c) The distribution of horizontally adjacent pixels in Figure 3(a). (d) The distribution of horizontally adjacent pixels in Figure 3(b).
Table 2. Comparison of running time and theirs performance.
3.6. Running Time Test
Three parallel algorithms are simulated in running time test. They are Zhou’s algorithm [13], Mirzaei’s algorithm [14] and the proposed algorithm. The encrypted image is gray 21.512 in USC-SIPI image database and the simulation results are described in Table 2.
4. Conclusion
In this paper, the security property of a class of image encryption algorithms based on chaotic maps bas been discussed. And some findings on the security problem of the existing parallel encryption algorithms have been reported. Based on discrete 2D-Logistic map, a self-adaptive parallel encryption algorithm has been developed according to the position scrambling and diffusion of multidirection in variable space of spatial chaos. The results of numerical analysis show that the proposed algorithm can meet the three requirements of parallel operation in image encryption and the real-time requirement in transmission processes. The security has been proved by theoretical analysis and simulation results.
5. Acknowledgements
The authors are greatly indebted to anonymous reviewers for their valuable comments and suggestions. This research is supported in part by the National Natural Science Foundation of China under Grant No. 60874091, the Six Projects Sponsoring Talent Summits of Jiangsu Province under Grant No. SJ209006, the Foundation for Doctoral Program of High Education of China under Grant No. 20103223110003, the MOE Research in the Humanities and Social Sciences Planning Fund of China (Grant No. 12YJAZH120), and the Postgraduate Scientific Innovation Project for Universities of Jiangsu Province under Grant No. CXZZ11-0401.