1. Introduction
In this article I would like to take you through a tour of the development of how a theoretical physicist, or a physics student, may derive a theory along the lines of the second approach described above. In particular we will begin with an intriguing aspect of curved space, defined below, and see how we can develop, and test, a theory. This could be viewed as a homework problem with hints: All you need to know is the physics and mathematics of a typical junior year course in electromagnetism. A little quantum mechanics would not hurt.
Motivation
First we must go back to the period 1905-1915, when Einstein began his quest to develop the general theory of relativity. At that time there was another problem that attracted the attention of physicists, the simple wheel. According to special relativity, if it is spinning, the circumference will suffer length contraction but the radius, being normal to direction of motion, will not contract. Thus either the value of π is not constant, or Euclidean geometry was wrong.
Another ingredient in this little tour of those years is Einstein’s Principle Equivalence. I will not discuss this in detail but will extract the main point: The mass of a test particle drops out of the equation F = ma when F contains m (the equality of inertial and gravitational mass).
These clues led Einstein to think in terms of geometry, where particles fall along geodesics in curved space. The biggest problem was, he did not know much about curved spaces! With his friend, Marcell Grossman teaching him, they learned Riemannian geometry together from published articles of Riemann’s work. A key ingredient of this geometry is the affine connection, a geometrical object denoted by . When a vector is parallel transported along a curve, the effect of curved space is to rotate the vector: The affine connection is a measure of that change in the vector. However, the concept of parallel transport was developed two years after Einstein published the theory of general relativity by Levi-Civita. Moreover, before that (1915) torsion was not known.
. When a vector is parallel transported along a curve, the effect of curved space is to rotate the vector: The affine connection is a measure of that change in the vector. However, the concept of parallel transport was developed two years after Einstein published the theory of general relativity by Levi-Civita. Moreover, before that (1915) torsion was not known.
The connection between the mathematics of curved space and physics is the rotation of the vector. Translating from Newtonian physics to GR, instead of saying the incorporeal gravitational field lines of Earth reach out and cause the apple to accelerate, we say Earth curves space and the apple follows along a geodesic. Thus all of the information about the motion of the apple is in the affine connection, quite a fine idea.
In fact these were Riemann’s ideas, but he lacked the contribution of Minkowski, who showed us the four dimensional spacetime in which we live. So the ideas of the previous paragraph only work out in four dimensional spacetime. I will often use the term space to stand for spacetime.
In the limited Riemannian geometry Einstein had to work with in 1915, the affine connection was symmetric. In this special case the affine connection is called the Christoffel symbol, usually denoted by  and the symmetry just mentioned means
and the symmetry just mentioned means . Howeversoon after 1915 the full geometry of curved space was developed and it was found that the affine connection is not, in general symmetric, and specifically the antisymmetric part is defined as the torsion,
. Howeversoon after 1915 the full geometry of curved space was developed and it was found that the affine connection is not, in general symmetric, and specifically the antisymmetric part is defined as the torsion,  , so that
, so that .
.
Now we may focus on “the intriguing aspect of curved space” I mentioned above, something not known when Einstein published his theory. Suppose we have two vectors A and B. They are in a plane (of course), originally with the bases touching. Here is a little thought experiment you may do. Parallel transport A along B and mark where the tip of A is. Call this trip one. Now go back and set the vectors as they were, but this time parallel transport B along A and mark the point where the tip of B is. Call this trip two. Is this the same point? In Euclidean geometry it is, and it is also the same point in Riemannian geometry, but in the richer non-Riemannian geometry (a poor name, but it means non-Riemannian and non-Euclidean) it is not the same point. In fact, the difference between these points is proportional to the torsion.
Is there physics here? Does the richer non-Riemannian geometry carry new physics just as Riemannian geometry did? If we ask what this little experiment is telling us, we must conclude that space can be endowed with a sense. In other words, in the experiment, in trip one, if you were going in an anticlockwise direction, then in trip two you were going clockwise. Thus in a geometry with torsion space has a sense or handedness that distinguishes between clockwise and anticlockwise. In GR we saw that the mass determines the affine connection of Riemannian space, so what physical quantity determines the sense? We assume it is a fundamental property of matter, like mass of charge, but unlike mass or charge it must have a direction, for otherwise it could not form a space that has a sense. Now we ask ourselves the simple question, what fundamental property of matter has a direction associated with it? There is only one, spin. With these ideas, we are led to suspect that spin is the source of torsion. More details on the geometry may be found in a previous article in Contemporary Physics [1].
As an aside, with this line of reasoning we achieve an egalitarian view of our fundamental particle parameters, just as mass create the gravitational field, and charge creates the electromagnetic field, now we have that spin creates the torsion field. It is emphasized that this is the intrinsic spin of elementary particles, not orbital angular momentum. This makes an interesting comparison with the celebrated “no hair” theorem of general relativity. This theorem states that a black hole can be described by only three parameters-mass, charge and spin the same parameters that give rise to the fundamental classical fields (other putative parameters, such as fields proportional to baryon number, is the hair, which is not allowed).
This brings us to the point of this article. We have theoretical reason to believe that spin creates a field, so what are the field equations? Using the undergraduate level mathematics we shall completely derive this theory, but first additional motivation is given.
The standard model of elementary particles, which is based on the concept of local gauge invariance, has shown to be a very successful theory. This formulation includes all the known forces in nature except gravitation. Not only is gravity left out, it is a theory that is non-renormalizable. That means, unlike electromagnetism, infinite quantities that appear cannot be canceled out by a change of definition in the mass and charge. In hopes of duplicating the success of the standard model, general relativity was also formulated as a local gauge theory [2], which I will now briefly describe. In that work, the torsion is given by the third rank tensor , which is the antisymmetric part of the affine connection.
, which is the antisymmetric part of the affine connection.
Let us consider a Lorentz transformation,  which takes us from one inertial reference frame to another. The elements of
which takes us from one inertial reference frame to another. The elements of  are constant (for inertial frames v is constant). But there is a problem here, first of all, in the presence of gravity, for example, reference frames will be accelerated. Second of all, since the
are constant (for inertial frames v is constant). But there is a problem here, first of all, in the presence of gravity, for example, reference frames will be accelerated. Second of all, since the  are constant, the transformation changes all of space instantaneously, which violates special relativity. A transformation that consists of constants and effects all of space instantly is called a global transformation.
are constant, the transformation changes all of space instantaneously, which violates special relativity. A transformation that consists of constants and effects all of space instantly is called a global transformation.
We know from special relativity that no information can be transmitted faster than c, the speed of light in vacuum. Paradoxically the Lorentz transformation does just that. This issue was raised first by Yang and Mills [3]. They argued that the global transformation that was used in nuclear physics (that instantaneously transformed protons to neutrons and vice verse) is unphysical, and in order to subscribe to the precepts of special relativity, it must be made local. This means that the constants of the transformation must be generalized to functions of space and time. There were still some issues to be resolved in this new “local gauge theory”, but today all of particle physics, the standard model, is based on this idea.
When the global Lorentz transformation is made local, one of the most beautiful results in physics occurs, we end up with general relativity. In fact, we end up with a little more then GR, in this development the torsion must exist in order to maintain a physical difference between translation and rotation, as shown so convincingly in [2]. The torsion is related to the rotational part of the Lorentz transformation so once again we see that, at the particle level, general relativity must include spin. Later, in more general gauge theories, it was found that a scaler field goes along with gravity and torsion [4].
A final and more recent motivation for the existence of torsion comes from string theory. String theory starts from a relativity simple idea, instead of assuming a particle, such as an electron, is a point, assume they are strings. The strings are so small 10–33 cm, there is no way to directly refute, or confirm, this notion. However, in order to have a consistent theory that makes sense, it turns out that there must be three fields: gravity, torsion, and the scalar field. The torsion field from string theory is often referred to as the Kalb-Ramond field [5], but it was quickly shown to be the torsion of non-Riemannian geometry [6]. In that work, the torsion is denoted by , where
, where  is the antisymmetric potential. So once again we see torsion must be included into a physical theory of gravity.
is the antisymmetric potential. So once again we see torsion must be included into a physical theory of gravity.
Finally I will point that in some formulations it appears that torsion may be optional, meaning that a perfectly consistent theory can be constructed without it. However, this is not the case, and recently it was shown why torsion is a necessary part of general relativity [7]. In this case it was shown that, in the absence of an external field, we have the total angular momentum plus spin is a conserved quantity. Without torsion the wrong result would occur, since spin would not be included.
With the development of a classical theory of spin, an old wound is opened. In particular, ever since its discovery, spin has been considered a “quantum” effect, with no classical counterpart. This would make torsion stand apart from our other classical theories gravity and electromagnetism. However this old saw is specious. There is nothing wrong with a classical theory of spin, what was shown was that spin cannot be accounted for by a rapidly rotating particle, which is true. As is exemplified below it is structure, not rotation, that gives rise to spin. In fact, a classical string is a perfect source for torsion.
Now we may proceed to the derivation of the field equations for torsion. Although it is usually described by arcane mathematics buried in a bigger theory of gravitation, often in the context of string theory in more than four dimensions, we will elucidate the theory of torsion in a basic way, deriving it following basic principles of physics and using electromagnetism as a guide.
In important caveat must be stated. This paper deals with torsion that is derived from a potential, often referred to as string theory torsion, or the Kalb-Ramond field. In the local gauge theories mentioned above, the torsion is taken to be the potential. Since torsion has never been measured we do not know which approach is correct, although several ideas carry over to both approaches.
2. Derivation of the Field Equations
Before we begin the derivation we can sketch a few basics. We will assume there is a source, spin, and this creates a field. If we perform a multipole expansion of the source, we must assume the lowest order term, the spherically symmetric term, does not exist. This is because spin, unlike charge or mass, is not a scalar quantity and therefore its field cannot be spherically symmetric. If there were a spherically symmetric part to the source, then no matter how small, at a large enough distance the spin would appear as spherically symmetric, which is wrong. The spin source is denoted by a vector, say N, which related to the spin (this is detailed in Section 4). The direction of the spin establishes a preferred direction in space. For this reason, in a multipole expansion of the field, the lowest order term is the dipole term, so if we call the field b, we expect
 (1)
(1)
where  is an unknown coupling constant, corresponding to the coupling constant in electromagnetism (the permittivity of vacuum in SI). In the following we will set c = 1 to avoid writing it every time a time derivative appears.
is an unknown coupling constant, corresponding to the coupling constant in electromagnetism (the permittivity of vacuum in SI). In the following we will set c = 1 to avoid writing it every time a time derivative appears.
The Potential
Now let us begin the derivation. We assume first that the field, like electromagnetism, must be covariant under coordinate transformations in Minkowski space. This means the equations must retain their form under such a transformation. This, in turn, tells us that the field cannot be a 3-vector: It must be a 4-vector (it could be a higher rank tensor, but we start with the simplest first). This means that there must be a fourth component of the field, say  such that we may make a 4-vector as
such that we may make a 4-vector as . This is analogous to the potential of electromagnetism, which consists of a vector A and a scalar
. This is analogous to the potential of electromagnetism, which consists of a vector A and a scalar 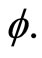 These are combined into the 4-vector potential (Although the same letter A is used for the potential for both torsion and electromagnetism, this should cause no confusion. One can distinguish them by looking at the other side of the equation).
These are combined into the 4-vector potential (Although the same letter A is used for the potential for both torsion and electromagnetism, this should cause no confusion. One can distinguish them by looking at the other side of the equation).
Next, we assume the fields (b and ) arise due to a source. We cannot build up such a theory starting from a scalar source (this gives the so called Klein Gordon equation, which was Schrödinger’s first attempt at the quantum equation), and the vector potential is already taken by electromagnetism. The next simplest case is a second rank tensor, but the symmetric second rank tensor is also taken, by gravitation. This leaves the antisymmetric tensor, which has six independent components. For example, the electromagnetic field tensor
) arise due to a source. We cannot build up such a theory starting from a scalar source (this gives the so called Klein Gordon equation, which was Schrödinger’s first attempt at the quantum equation), and the vector potential is already taken by electromagnetism. The next simplest case is a second rank tensor, but the symmetric second rank tensor is also taken, by gravitation. This leaves the antisymmetric tensor, which has six independent components. For example, the electromagnetic field tensor  is an example of an antisymmetric second rank tensor, with the six components representing the two vectors of the electric field and magnetic induction (in vacuum). Thus we assume the torsion source may be represented by two vectors, say N and I.
is an example of an antisymmetric second rank tensor, with the six components representing the two vectors of the electric field and magnetic induction (in vacuum). Thus we assume the torsion source may be represented by two vectors, say N and I.
Now, like E & M, we assume that the theory should give rise to linear, second order differential equations in terms of the potential. Thus the fields should be given by some first order differential operator, DO, such that b = (DO A). The obvious operator is the curl (the divergence would yield a scalar, and the gradient would not yield a vector), so we have the putative equation,

Also, for , we expect
, we expect  = DO a. In order to turn a vector into a scalar it is evident the choice of the DO is divergence, so we have
= DO a. In order to turn a vector into a scalar it is evident the choice of the DO is divergence, so we have
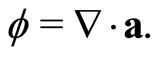 (2)
(2)
A troubling aspect of these two equations is that, unlike E & M, there is no time derivative. Moreover, in the theory of E & M we know that the existence of the potential automatically gives rise to two of Maxwell equations, so let’s see if this gives us a clue. Looking at the putative equation we have, since the divergence of curl is zero, . Now we clearly see that the lack of time dependence has gotten us in trouble, for such an equation cannot be relativistically covariant. As argued above it must have a fourth component. In fact, using the generalization that, when going to 3-space to Minkowski space we have
. Now we clearly see that the lack of time dependence has gotten us in trouble, for such an equation cannot be relativistically covariant. As argued above it must have a fourth component. In fact, using the generalization that, when going to 3-space to Minkowski space we have , we should expect, in place of
, we should expect, in place of ,
,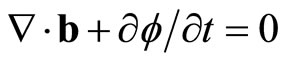 . The easiest way to get this equation is to add the term
. The easiest way to get this equation is to add the term 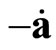 to the putative equation, so that we have
to the putative equation, so that we have
 (3)
(3)
Another important property of electromagnetism is gauge invariance, and we expect to have gauge invariance in this theory as well. From Equation (2) we see that, since the divergence of the curl vanishes, we might try  where
where 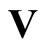 is some vector. This means that the simplest the potential can be is a vector, and as explained above, there must be a fourth component, say
is some vector. This means that the simplest the potential can be is a vector, and as explained above, there must be a fourth component, say . This fits with Equation (3), since the curl of the gradient of a scalar vanishes. Thus we may also consider
. This fits with Equation (3), since the curl of the gradient of a scalar vanishes. Thus we may also consider 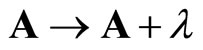 where
where  is some scalar. This does not quite work however, due to the presence of
is some scalar. This does not quite work however, due to the presence of  in Equation (3). This is easy enough to correct: we simply add
in Equation (3). This is easy enough to correct: we simply add  to
to . With this we have full gauge invariance, shown in Figure 1.
. With this we have full gauge invariance, shown in Figure 1.
3. The Field
Now let us try and deduce the field equations. From the assumption that they are linear and of second differential order in terms of the potential we expect, like E & M, equations of the form: Field = DO source. Starting with b, once again we look for a DO that turns a vector into a vector, and once again the choice is the curl. Thus we assume
 (4)
(4)
An important consequence of this is that N is not totally arbitrary. Since the divergence of the curl vanishes, we must have . This will be used later.
. This will be used later.
For , we seek a DO that turns a scalar into a vector. Therefore this DO must be the gradient operator, so we postulate
, we seek a DO that turns a scalar into a vector. Therefore this DO must be the gradient operator, so we postulate

but there is a problem. Once again time dependence is lost. For example, Newton’s theory of gravitation is time independent, which implies forces act instantaneously. This violates special relativity and therefore any time independent theory cannot satisfy special relativity. Suppose we consider the vacuum equation: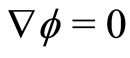 . Now consider the identity we found earlier,
. Now consider the identity we found earlier, . Since the order of partial differentiation commutes, we can take the gradient of this and get,
. Since the order of partial differentiation commutes, we can take the gradient of this and get,
 or with the previous equation,
or with the previous equation, . Now we can use the vector identity
. Now we can use the vector identity
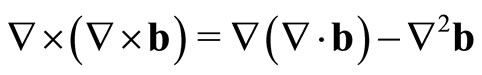 (5)
(5)
and equate the last two terms, since the curl of b is zero in vacuum. This yields —an unacceptable result.
—an unacceptable result.
The only assumption that was made was that we are considering the vacuum case, but once again time dependence is lost. Checking with E & M for a clue, we know that in vacuum the field components obey the wave equation, . We can trace this second time derivative to Faraday’s law. This is the clue that lets us suspect the postulated equation should be modified so that
. We can trace this second time derivative to Faraday’s law. This is the clue that lets us suspect the postulated equation should be modified so that
 (6)
(6)
Reproducing the previous steps results in
 (7)
(7)
an acceptable result. Thus, we have two field equations (as opposed to four vector equations of E & M) given by Equations (4) and (6). We also recognize (7) as the wave equation, and therefore predict that, like electromagnetism, torsion produces waves that travel at the speed of light. It may also be shown that the potential satisfies the wave equation in the correct gauge [8]. These are summarized in Figure 2.

Figure 1. Comparison of fields from a potential and gauge invariance.
It should be noted that Equation (1) is a solution to Equation (4) exterior to the source. This gives rise to the field that was discussed in the introduction. We also see in retrospect that we did not have to assume such a form as Equation (1). Once we took the potential to be a pair of vectors, the simplest case excluding known fields, the result was inevitable.
4. Tensor Formulation and String Theory
Vector formulation in Euclidean space, as done above, breaks 4-vectors into the space part and a scalar (in 3D). This complicates the mathematics and it turns out many things are easier to see in terms of a tensor formulation in Minkowski space. For example in electromagnetism we start with a 4-vector potential . A surefire way to obtain a tensor is by taking the antisymmetric derivative
. A surefire way to obtain a tensor is by taking the antisymmetric derivative  (
( ). This holds in Riemannian geometry as well. In this case we started with a tensor of rank one, the potential, and generated the field. The next simplest approach is to start with a second rank tensor, say
). This holds in Riemannian geometry as well. In this case we started with a tensor of rank one, the potential, and generated the field. The next simplest approach is to start with a second rank tensor, say  and define the field according
and define the field according
 (8)
(8)
(the brackets imply taking the antisymmetric part, which is written explicitly on the right hand side). The field equations are, as before given by some DO on . The obvious choice is
. The obvious choice is . We also write the source as an antisymmetric tensor
. We also write the source as an antisymmetric tensor  so that we expect
so that we expect
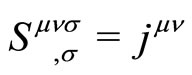 (9)
(9)
(we sum over ). Gauge invariance is especially easy,
). Gauge invariance is especially easy,
 (10)
(10)
as demonstrated in Figure 3.
The detailed relationship between the 3-vectors and the tensor components may be found elsewhere [9].
Now let us a consider the string again. In the literature the phrase “string theory” usually means “superstring theory” which means “supersymmetric string theory”. Supersymmetry postulates a symmetry between bosons and fermions. Although they seem to be quite separate, with their own conservation laws (conservation of baryon number, etc.), at high enough energies these transformations are expected to occur. The infinities exactly cancel out if supersymmetry is invoked, that is, the infinity from the boson sector cancels out the infinity from the fermion sector (at least at leading order), and the theory may be made free of infinities.
String theorists claim than nothing the theory predicts has been shown to be false, making it a viable theory. Those who are not taken by the mathematical beauty say that nothing that string theory predicts has been observed (or worse, everything string theory predicts is wrong).

Figure 2. The field equations and potential in terms of the source for electromagnetism and torsion.

Figure 3. The tensor fields are given in terms of the source.
These quantities refer to things like the number of dimensions in which we must live (10 or 11), and the many superpartners, like the neutralino.
I was dubious, but then I found that strings really do fall into gravitation with torsion in a natural way. It all starts with the source. Let us look at the conventional (no string) multipole expansion of a vector source of electromagnetism [10],
 (11)
(11)
where x goes from the origin to the point at which the field is evaluated and x' goes from the origin to a point in the source. If the divergence of J (we are considering magnetostatics here) is zero the first term vanishes and the second term may be written such that
 (12)
(12)
where  [10].
[10].
The same thing happens for torsion. The easiest way to see this is an examination of Figure 4 which compares electromagnetism and torsion. The first line shows each has a vector source. The second line shows that the curl of field in each case is equal to the source. The third line represents the source. The delta function insures that the particle is traveling along the worldline parameterized by . The second part of the equations show how the source density,
. The second part of the equations show how the source density,  ,
,  are defined. The major difference is that torsion has an intrinsic vector
are defined. The major difference is that torsion has an intrinsic vector . In the case of E & M the source is the density multiplied by the velocity, but no such equation is allowed for torsion since we know that spin cannot be accounted for by motion. This is why there is the intrinsic vector. With this, in the last line of this table we see how the spin is defined, integrating the cross product of the position vector with the source,
. In the case of E & M the source is the density multiplied by the velocity, but no such equation is allowed for torsion since we know that spin cannot be accounted for by motion. This is why there is the intrinsic vector. With this, in the last line of this table we see how the spin is defined, integrating the cross product of the position vector with the source,  , with
, with .
.

Figure 4. Comparison of torsion and electromagnetism regarding the source.
This is very important. It shows that intrinsic spin results from structure, not from any spinning motion. In fact there is a harbinger of this result from quantum mechanics. Suppose we picture  where
where  is the solution to the Schrödinger equation, for various quantum numbers, n and l. If the angular momentum is zero (
is the solution to the Schrödinger equation, for various quantum numbers, n and l. If the angular momentum is zero ( ) then
) then  is spherically symmetric. Non-zero angular momentum states, while static, are not spherically symmetric. This suggests that angular momentum, quantum mechanically, should be pictured as arising from structure. For intrinsic spin, the above shows that it results from the structure of the source.
is spherically symmetric. Non-zero angular momentum states, while static, are not spherically symmetric. This suggests that angular momentum, quantum mechanically, should be pictured as arising from structure. For intrinsic spin, the above shows that it results from the structure of the source.
Originally I did not have a physical picture of the intrinsic vector. But when the theory is formulated in curved space, the action is the same as that used in string theory. It was natural to assume, then, the source of torsion should be the string. This turns out to be right, and the intrinsic vector invented above turns out to be the tangent vector to the string.
To see this in particular let us discuss the classical string. The string is a natural generalization of a point. Suppose we consider the conventional formulation of electrodynamics. The action is
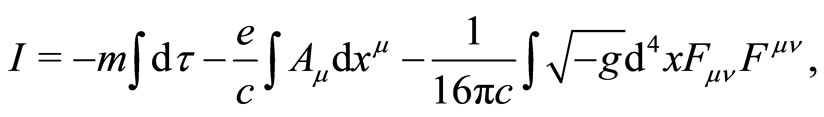 (13)
(13)
where we focus on the first term. This represents a point particle traveling along the worldline parameterized by .
.
A string has two coordinates. One is , which is like the
, which is like the  coordinate used for the point particle, and the other is
coordinate used for the point particle, and the other is  which gives the object length, i.e., makes it a string. The string space spanned by these two coordinates is called the parameter space, while the space in which we shall make our measurements, described by the coordinates
which gives the object length, i.e., makes it a string. The string space spanned by these two coordinates is called the parameter space, while the space in which we shall make our measurements, described by the coordinates , is called the target space. When the string is quantized it is found that the theory only makes sense in 26 dimensions for the bosonic string and 10 or 11 for the fermionic case, but we do not care about that. We are establishing a classical theory so we are happy to keep to a four dimensional spacetime (target space).
, is called the target space. When the string is quantized it is found that the theory only makes sense in 26 dimensions for the bosonic string and 10 or 11 for the fermionic case, but we do not care about that. We are establishing a classical theory so we are happy to keep to a four dimensional spacetime (target space).
To reduce indices we will let  and
and . In the target space a point on the string is
. In the target space a point on the string is  and we can find the tangent vectors by differentiation,
and we can find the tangent vectors by differentiation,
 (14)
(14)
From these we may build an area element of the string in target space,
 (15)
(15)
One may consider that the area between two vectors is equal to the magnitude of the cross product, and for any given 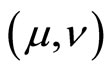 the terms in (14) are essentially a cross product. For details in a very readable account one may consult the book by Zwiebach [11].
the terms in (14) are essentially a cross product. For details in a very readable account one may consult the book by Zwiebach [11].
Now, if we want to generalize this first term in (12) to a string we have two choices. The first is
 (16)
(16)
where the mass m is replaced by the mass per unit length . The second choice is to couple an antisymmetric tensor to
. The second choice is to couple an antisymmetric tensor to  (note that from its definition
(note that from its definition  is antisymmetric, so only an antisymmetric tensor coupling gives non-zero results).
is antisymmetric, so only an antisymmetric tensor coupling gives non-zero results).
All this is great news for physics with torsion (as described in the introduction). The first choice can be used to describe matter and the second term may be coupled to , the torsion potential. This is a very natural coupling and was first discovered by Kalb and Ramond [5]. It turns out the intrinsic vector is replaced by the tangent vector to the string. Thus, the string is a very natural source for torsion and, in fact, one may say torsion demands the use of torsion (in general, strings can be open or closed. In the following I assume they are closed, so that they make tiny loops).
, the torsion potential. This is a very natural coupling and was first discovered by Kalb and Ramond [5]. It turns out the intrinsic vector is replaced by the tangent vector to the string. Thus, the string is a very natural source for torsion and, in fact, one may say torsion demands the use of torsion (in general, strings can be open or closed. In the following I assume they are closed, so that they make tiny loops).
We may see explicitly why strings give rise to torsion. As mentioned above, the coupling is between the torsion potential and the area element, so the action has a term
 (17)
(17)
To obtain the field equations variations are taken with respect to the potential, so the term multiplying the potential is taken to be the source. For example, without the string we used
 (18)
(18)
so that  is the source. With (16) we see that the string is the source. This is the beautiful result that strings have spin, and give to a theory of classical spin. In fact, it was shown that the value of the spin is proportion to area of enclosed by the string, a very geometric result emphasizing the earlier remarks that spin arises from structure, not rotation [12].
is the source. With (16) we see that the string is the source. This is the beautiful result that strings have spin, and give to a theory of classical spin. In fact, it was shown that the value of the spin is proportion to area of enclosed by the string, a very geometric result emphasizing the earlier remarks that spin arises from structure, not rotation [12].
5. Physical Manifestations and Summary
This completes the development of theory, and the first question should be, how do we measure it? It has been shown that a particle with spin S in a torsion field b has the potential energy
 (19)
(19)
where the coupling constant is written as  where
where .
.
So far torsion has not been discovered experimentally. Several searches have been tried [13,14], but these experiments only put an upper bound on the coupling constant. In these searches a potential of the general form
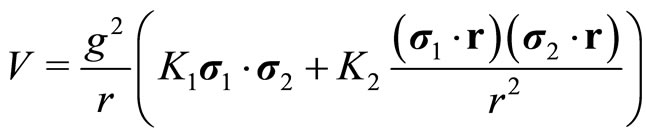 (20)
(20)
was assumed, there  and
and  atr constants to be found and
atr constants to be found and  represnts the spin. For the case of a dipole field
represnts the spin. For the case of a dipole field . The first notion that may come to mind is hydrogen. We should expect the spin one-half proton to interact with the spin one-half electron. This is not to be confused with the “spin-spin” interaction which gives rise to the hyperfine structure. That effect is really the “magnetic moment-magnetic moment” interaction. The torsion will give rise to an additional splitting. However, this is not seen, so we immediately place an upper bound on the torsion coupling constant. From the experimental data on the energy levels of hydrogen [16], we conclude that the energy levels are known to about 10–10 eV, so that
. The first notion that may come to mind is hydrogen. We should expect the spin one-half proton to interact with the spin one-half electron. This is not to be confused with the “spin-spin” interaction which gives rise to the hyperfine structure. That effect is really the “magnetic moment-magnetic moment” interaction. The torsion will give rise to an additional splitting. However, this is not seen, so we immediately place an upper bound on the torsion coupling constant. From the experimental data on the energy levels of hydrogen [16], we conclude that the energy levels are known to about 10–10 eV, so that 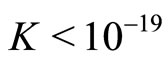 s/g [15]. More refined experiments find the upper bound to be about three orders of magnitude smaller than this [13,14]. More recently Qui and Shao have examined this theory and found a better bound on the coupling constant [17].
s/g [15]. More refined experiments find the upper bound to be about three orders of magnitude smaller than this [13,14]. More recently Qui and Shao have examined this theory and found a better bound on the coupling constant [17].
Although there are other physical manifestations of torsion, such as spin flipping [18] and a nonlinear quantum equation [19], recently I gave been working on an entirely new approach to measuring torsion. Unlike gravitational waves, which take an enormous accelerating mass to generate waves of appreciable magnitude, the power of torsion waves depends on spin. In fact, following along the line of E & M, we can calculate the power emitted from a source. For N spins flipping at frequency , I found the source emits power proportional to
, I found the source emits power proportional to . The key, therefore is to flip as many spins as possible at the highest frequency possible. This approach is still in progress, since a source and a detector must be selected.
. The key, therefore is to flip as many spins as possible at the highest frequency possible. This approach is still in progress, since a source and a detector must be selected.
Two final comments. The first concerns the source of torsion, the intrinsic spin. Just as in E & M, or in general relativity, the source must be prescribed. It is not enough to simply say there are a pair of vectors N and I. This has been done in detail elsewhere [20], although subsequently I discovered a very beautiful result: The source of the torsion arises naturally from strings. Thus, using a string, both gravity and spin and be described-the interpretation being that strings have spin [12]. This holds in the limit that the source is stationary. Thus, intrinsic spin does not arise from rotation, but from the geometry of the source.
The final comment is that this theory is unique within the assumptions given. However, there are other theories of torsion. In gauge theories torsion is the potential, and a field is derived in terms of that. Older work has torsion as the link for unified theories and gravity and electromagnetism. In the earliest work by Einstein and Cartan, called teleparallel theories, the torsion represented the matter of spacetime [21].
NOTES