Lock-in-Amplifier Model for Analyzing the Behavior of Signal Harmonics in Magnetic Particle Imaging ()
1. Introduction
In 2005, a new imaging method called magnetic particle imaging (MPI) was introduced [1] . MPI allows for imaging of the spatial distribution of magnetic nanoparticles (MNPs) with high sensitivity, high spatial resolution, and high imaging speed.
MPI utilizes the nonlinear response of MNPs to detect their presence in an alternating magnetic field called the drive magnetic field. Spatial encoding is accomplished by saturating the magnetization of the MNPs almost everywhere except in the vicinity of a special region called the field-free point (FFP) or field-free line (FFL) using a static magnetic field called the selection magnetic field [1] .
Due to the nonlinear response of the MNPs to an applied drive magnetic field, the signals generated by the MNPs in a receiving coil contain not only the excitation frequency but also the harmonics of this frequency. These harmonics are used for image reconstruction in MPI [1] . Thus, the qualitative and quantitative properties of MPI directly depend on the characteristics of these harmonics. It is also known that the magnetization response of MNPs depends not only on the magnetic properties of MNPs but also on the particle size and distribution of MNPs [2] .
For a better understanding and optimization of MPI, it is important to investigate the behavior of signal harmonics generated by MNPs under various conditions of the drive and selection magnetic fields and their dependence on the particle size and distribution of MNPs. We previously investigated the behavior of signal harmonics in MPI by experimental and simulation studies, and reported that it largely depended on the strength of the drive and selection magnetic fields and the particle size distribution of MNPs [3] . In our previous studies, signal harmonics were calculated from the spectra obtained by the Fourier transformation of the signals induced by MNPs in a receiving coil [3] .
Lock-in amplifiers were invented in the early 1940s to extract electrical signals in extremely noisy environments [4] . They employ a homodyne detection scheme and low-pass filtering to measure the electrical signal relative to a periodic reference signal. They extract signals in a defined frequency band around the reference frequency, efficiently rejecting all other frequency components. They are also often used to extract signals in the field of MPI [5] [6] .
The purpose of this study was to present a lock-in-amplifier model for analyzing the behavior of signal harmonics in MPI and some simulation results based on this model.
2. Materials and Methods
2.1. Lock-in-Amplifier Model
Figure 1 illustrates a lock-in-amplifier model. A lock-in amplifier performs a multiplication of its input with a reference signal, and then applies an adjustable low-pass filter to the result. The multiplication is called “signal mixing”, as illustrated
![]()
Figure 1. Illustration of a lock-in-amplifier model. The input signal
is multiplied by the reference signal
and then the mixed signal
is low-pass filtered to reject the noise and finally converted to the output signal
.
by ⨂ in Figure 1. The signal mixing is mathematically expressed as a multiplication of the input signal
with the complex reference signal
, which is given by
(1)
where
denotes the signal after mixing and
is given by
(2)
In Equation (2),
and
denotes the frequency of the reference signal. The mixed signal is then fed through a low-pass filter to extract the DC component of the signal. Mathematically, this procedure is given by
(3)
where
and
denote the Fourier transforms (
) of the output signal
and
, respectively, i.e.,
and
.
denotes the transfer function of the first-order RC low-pass filter and is well approximated by
(4)
where
is the filter time constant with resistance R and capacitance C (Figure 1). It is well known that the unit step response of the first-order RC
low-pass filter in the time domain
is given by
(5)
Figure 2(a) and Figure 2(b) show
in a Bode plot, i.e.,
as a function of
and
for various τ values, respectively.
is obtained by the inverse Fourier transformation (
) of
, i.e.,
and is given by
(6)
![]()
Figure 2. (a) Transfer function of the first-order RC low-pass filter
given by Equation (4) in a Bode plot, i.e.,
as a function of
, for various values of the time constant of the low-pass filter used in the lock-in amplifier (τ); (b) Unit step response of the first-order RC low-pass filter in the time domain given by Equation (5) for various τ values.
where
and
denote the absolute value of
and phase at time t, respectively. In this study, the MPI signal (
) is defined as the mean of
, i.e.,
(7)
2.2. Signals Induced by MNPs
Assuming a single receiving coil with sensitivity
at spatial position r, the changing magnetization induces a voltage according to Faraday’s law
,
which is given by [7]
(8)
where Ω denotes the volume containing MNPs,
is the concentration of MNPs at position r,
is the magnetization at position r and time t, and
is the magnetic permeability of a vacuum.
is the receiving coil sensitivity derived from the magnetic field that the coil would produce if driven with a unit current [7] .
In the following, the receiving coil sensitivity is assumed to be constant and uniform over the volume of interest and is denoted by
. When we consider the signal generated by a point-like distribution of MNPs, that is, the MNP distribution is approximated by Dirac’s δ function such that
with
being constant, the volume integral in Equation (8) vanishes and
given by Equation (8) is reduced to
(9)
Note that
is denoted by
in Equation (9) for simplicity. We can neglect constant factors in Equation (9).
In addition, we assume that the signal obtained by the receiving coil includes Gaussian white noise [8] . Thus, the input signal to a lock-in amplifier [
in Figure 1] is calculated by
(10)
where
, randn, and SNR denote the mean of
, a normally-distributed random number with zero mean and unit variance, and signal-to-noise ratio, respectively.
2.3. Langevin Function
Assuming that MNPs are in equilibrium, the magnetization of MNPs in response to an applied magnetic field can be described by the Langevin function [9] , which is given by
(11)
where M0 is the saturation magnetization and ξ is the ratio of the magnetic energy of a particle with magnetic moment m in an external magnetic field H to the thermal energy given by the Boltzmann constant kB and the absolute temperature T:
(12)
In Equation (12),
is the domain magnetization of a suspended particle, and
is the magnetic volume given by
for a particle of diameter D.
In this study, we assume that the external magnetic field at position x and
time t
is given by
(13)
where
is the strength of the selection magnetic field at position x and
is the strength of the drive magnetic field at time t. We also assume that
is given by
(14)
where
and
denote the amplitude and frequency of the drive magnetic field, respectively. Furthermore, we assume that
is given by
(15)
where Gx and x denote the gradient strength of the selection magnetic field and the distance from the field-free region, respectively.
2.4. Particle Size Distribution
When the particle size distribution obeys a log-normal distribution [10] , the magnetization of MNPs averaged based on this particle size distribution
is given by [3]
(16)
where
denotes the magnetization of MNPs with diameter D. μ and σ denote the mean and standard deviation (SD) of the log-normal distribution, respectively [3] . It should be noted that the relationships between μ and D and between σ and D are represented by
(17)
and
(18)
respectively, where
and
denote the expectation and variance of D, respectively.
2.5. Simulation Studies
In this study, we considered magnetite (Fe3O4) as MNPs, and Md in Equation (11) was taken as 446 kA/m [3] . The amplitude and frequency of the drive magnetic field [
and
in Equation (14), respectively] were fixed at 10 mT and 400 Hz, respectively [5] [6] , and the temperature was assumed to be room temperature (293.15 K) in all simulation studies. Since the frequency of the drive magnetic field was fixed at 400 Hz as described above, the third-harmonic MPI signal corresponds to the
value given by Equation (7) at
.
Unless specifically stated,
and σ in Equation (17) and Equation (18) were assumed to be 20 nm and 0.2, respectively, and Gx in Equation (15) was assumed to be 2 T/m. When investigating the dependence of the odd- and even-numbered harmonics on the selection magnetic field, Gx in Equation (15) was varied from 1 to 5 T/m. When investigating the dependence of the third-harmonic signal on the particle size of MNPs,
and σ in Equation (17) and Equation (18) were varied from 10 to 50 nm and from 0.05 to 0.4, respectively.
3. Results
Figure 3(a) and Figure 3(b) show examples of
and
, respectively. Figure 3(c) shows
obtained from
and
by the inverse Fourier transformation of
given by Equation (3). In these cases, the MNPs were assumed to be located at the center of the field-free region, i.e.,
.
was taken as 1200 Hz. The time constant of the low-pass filter used in the lock-in amplifier (τ) and SNR were assumed to be 10 ms and 20, respectively.
![]()
Figure 3. (a) Example of
; (b) Example of
; (c)
obtained from
and
by the inverse Fourier transformation of
given by Equation (3).
Figure 4 shows the relationship between the MPI signal given by Equation (7) (
) and the distance from the field-free region (x) for the odd-numbered harmonics, whereas Figure 5 shows those for the even-numbered harmonics. In these cases, the gradient strength of the selection magnetic field [Gx in Equation (15)] was taken as 2 T/m. As in Figure 3, τ and SNR were assumed to be 10 ms and 20, respectively. As shown in Figure 4 and Figure 5, the odd-numbered harmonics are not zero at
, whereas the even-numbered harmonics are zero at
. The
value at the peak for the third-harmonic signal was the largest of the studied odd-numbered harmonics and that for the second-harmonic signal was the largest of the studied even-numbered harmonics. As shown in Figure 5, the oscillation including the dent characteristic of each harmonic signal was observed and the number of the dent increased with increasing order of the harmonics for both the odd- and even-numbered harmonics.
Figure 6 shows the relationship between the third-harmonic MPI signal, i.e.,
at
and x when Gx was varied from 1 to 5 T/m. The other parameters were the same as in Figure 4 and Figure 5. As shown in Figure 6, the plot of
versus x was scaled by a factor of Gx in the x axis, because
was assumed to be proportional to Gx as given by Equation (15).
Figure 7 shows the relationship between the third-harmonic MPI signal and x when τ was varied from 10 μs to 100 ms, whereas the other parameters were the same as in Figure 6. As shown in Figure 7, the dent at
decreased with increasing τ value.
Figure 8 shows the coefficient of variation (CV) of the third-harmonic MPI signal as a function of τ for various SNR values of the input signal. It should be noted that the CV is defined as the ratio of the SD to the mean value. Figure 8(a) shows the case for x of 0 cm, and Figure 8(b) the case for x of 1 cm. The CV value decreased with increasing τ value. When
[Figure 8(a)], the dependency on SNR was smaller than when
[Figure 8(b)].
![]()
Figure 4. Relationship between the MPI signal (
) given by Equation (7) and the distance from the field-free region (x) for the odd-numbered harmonics in the case when the gradient strength of the selection magnetic field (
) is 2 T/m.
![]()
Figure 5. Relationship between SMPI and x for the even-numbered harmonics in the case when Gx is 2 T/m.
![]()
Figure 6. Relationship between the third-harmonic MPI signal, i.e.,
at
and x when
was varied from 1 to 5 T/m.
![]()
Figure 7. Relationship between the third-harmonic MPI signal and x when τ was varied from 10 μs to 100 ms.
![]()
Figure 8. Coefficient of variation (CV) of the third-harmonic MPI signal as a function of τ for various signal-to-noise (SNR) values of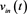 . (a) is the case for x of 0 cm; and (b) is the case for x of 1 cm.
. (a) is the case for x of 0 cm; and (b) is the case for x of 1 cm.
Figure 9 shows a comparison of the relationship between 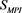 and x when the third harmonics alone and multiple odd-numbered harmonics were used. The
and x when the third harmonics alone and multiple odd-numbered harmonics were used. The 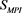 value at
value at 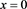 increased and the dent at
increased and the dent at 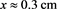 decreased as the number of added odd-numbered harmonics increased.
decreased as the number of added odd-numbered harmonics increased.
Figure 10 shows a comparison of the relationship between the third-harmonic MPI signal and x when 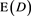 in Equation (17) was varied from 10 to 50 nm. As shown in Figure 10, the third-harmonic MPI signal largely depended on
in Equation (17) was varied from 10 to 50 nm. As shown in Figure 10, the third-harmonic MPI signal largely depended on 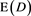 of MNPs.
of MNPs.
Figure 11 shows a comparison of the relationship between the third-harmonic MPI signal and x when the σ value given by Equation (18) was varied from 0.05 to 0.4. Although the third-harmonic MPI signal also depended on σ, its effect was much smaller than that of 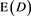 (Figure 10).
(Figure 10).
![]()
Figure 9. Relationship between SMPI and x when only the third-harmonic signal or multiple odd-numbered harmonics were used. The red, yellow, green, and blue curves represent cases when only the third-harmonic signal was used, the third- to 7th-harmonic signals were added, the third- to 13th-harmonic signals were added, and the third- to 19th-harmonic signals were added, respectively.
![]()
Figure 10. Relationship between the third-harmonic MPI signal and
when
in Equation (17) was varied from 10 to 50 nm.
![]()
Figure 11. Relationship between the third-harmonic MPI signal and x when the σ value given by Equation (18) was varied from 0.05 to 0.4.
4. Discussion
We previously investigated the behavior of signal harmonics in MPI and reported that the behavior of the odd- and even-numbered harmonics of MPI signals largely depends not only on the strength of the drive and selection magnetic fields but also on the particle size distribution of MNPs [3] . In our previous study, the signal harmonics were calculated from the spectra obtained by the Fourier transformation of the signal generated by MNPs in a receiving coil [3] . In considering the practical application of MPI, it would be important to distinguish the signals generated by the MNPs from those induced by the receiving coil itself and to remove this feed through interference [3] [5] [6] . Furthermore, it would be important to increase the SNR of MPI signals, especially when the SNR is low.
Lock-in amplifiers are often used to extract signals in MPI [5] [6] because they are effective for extracting signals in extremely noisy environments [4] . In this paper, we presented a lock-in-amplifier model for analyzing the behavior of signal harmonics in MPI and some simulation results based on this model (Figures 4-11). Our results demonstrated that the behavior of the MPI signals depends on the parameters in the lock-in amplifier such as the time constant of the low-pass filter (Figure 7 and Figure 8).
We simulated the magnetization of MNPs in response to the drive magnetic field by using the Langevin function given by Equation (11). This is one of the most extensively studied models in MPI and is based on the assumption that MNPs are in equilibrium [11] . This appears to be valid at the low frequency of the drive magnetic field where the magnetization of MNPs is in equilibrium. As the frequency of the drive magnetic field increases, a relaxation time governs the ability of MNPs to follow changes in the drive magnetic field via two distinct relaxation mechanisms; the Néel and Brownian mechanisms [12] . In the Néel mechanism, internal reorientation of the magnetic moment of MNPs occurs, whereas physical rotation of MNPs occurs in the Brownian mechanism, and its characteristic time (![]() ) is proportional to the viscosity of the suspending solvent [12] . As previously described, the frequency of the drive magnetic field was set at 400 Hz in this study, which is much lower than the reciprocal of
) is proportional to the viscosity of the suspending solvent [12] . As previously described, the frequency of the drive magnetic field was set at 400 Hz in this study, which is much lower than the reciprocal of![]() . Thus, the effect of viscosity appears to be negligible in this study. When this effect cannot be neglected, however, it would be necessary to perform more detailed analysis based on the stochastic Langevin equation considering Néel relaxation and Brownian rotation simultaneously [11] [13] .
. Thus, the effect of viscosity appears to be negligible in this study. When this effect cannot be neglected, however, it would be necessary to perform more detailed analysis based on the stochastic Langevin equation considering Néel relaxation and Brownian rotation simultaneously [11] [13] .
Because not all particles in a certain volume have the same diameter D, the magnetization of MNPs should be averaged based on the particle size distribution. The result of a natural growth process during particle synthesis does not yield particles with a single diameter D, but particles with a polydispersed particle size distribution [10] . A reasonable and commonly used approach for modeling is the log-normal distribution [10] . Thus, we assumed that the particle size distribution obeys a log-normal distribution [10] . In this case, the averaged magnetization of MNPs ![]() is given by Equation (16).
is given by Equation (16).
Theoretically, the odd-numbered harmonics should not be zero, whereas the even-numbered harmonics should be zero when the selection magnetic field is not applied, i.e., at the center of the field-free region such as FFP or FFL [3] . Our results (Figure 4 and Figure 5) showed that the odd-numbered harmonics were not zero and even-numbered harmonics were almost zero at![]() , as expected theoretically [3] . These results are also consistent with those previously obtained experimentally [3] . Furthermore, the third-harmonic signal was the largest of the studied odd-numbered harmonics (Figure 4). As previously described, the odd-numbered harmonics are generally used for image reconstruction in MPI [1] because their signals appear at the field-free region and decrease while oscillating outside the field-free region as shown in Figure 4, from which the spatial distribution of MNPs can be encoded. Since the third-harmonic signal at the center of the field-free region is the largest of the odd-numbered harmonics except for the first-harmonic signal as shown in Figure 4, it is commonly exploited for image reconstruction in MPI [5] [6] .
, as expected theoretically [3] . These results are also consistent with those previously obtained experimentally [3] . Furthermore, the third-harmonic signal was the largest of the studied odd-numbered harmonics (Figure 4). As previously described, the odd-numbered harmonics are generally used for image reconstruction in MPI [1] because their signals appear at the field-free region and decrease while oscillating outside the field-free region as shown in Figure 4, from which the spatial distribution of MNPs can be encoded. Since the third-harmonic signal at the center of the field-free region is the largest of the odd-numbered harmonics except for the first-harmonic signal as shown in Figure 4, it is commonly exploited for image reconstruction in MPI [5] [6] .
The relationship between the MPI signal [![]() given by Equation (7)] and the distance from the field-free region (x) [Figure 4, Figure 6, Figure 7, and Figures 9-11] appears to correspond to the system function in the spatial domain in MPI. In projection-based MPI [5] [6] [14] , the projection data are considered to be given by the convolution between the line integral of the concentration of MNPs through the FFL and the system function in the spatial domain, implying that the quantitative property of MPI can be enhanced by deconvolution of the system function from the projection data [14] .
given by Equation (7)] and the distance from the field-free region (x) [Figure 4, Figure 6, Figure 7, and Figures 9-11] appears to correspond to the system function in the spatial domain in MPI. In projection-based MPI [5] [6] [14] , the projection data are considered to be given by the convolution between the line integral of the concentration of MNPs through the FFL and the system function in the spatial domain, implying that the quantitative property of MPI can be enhanced by deconvolution of the system function from the projection data [14] .
As shown in Figure 7, the relationship between the MPI signal and x largely depended on the τ value in the low-pass filter [Equation (4)]. The dent at ![]() decreased with decreasing τ value. This appears to be mainly due to the increase in contamination of harmonics other than the third harmonics. In contrast, the CV value increased with decreasing τ value (Figure 8). Furthermore, as shown in Figure 2(b), the delay in the unit step response increases with increasing τ value, which will cause blurring in MPI [14] . Thus, it is important to select an appropriate value for τ in the low-pass filter by taking these factors into consideration.
decreased with decreasing τ value. This appears to be mainly due to the increase in contamination of harmonics other than the third harmonics. In contrast, the CV value increased with decreasing τ value (Figure 8). Furthermore, as shown in Figure 2(b), the delay in the unit step response increases with increasing τ value, which will cause blurring in MPI [14] . Thus, it is important to select an appropriate value for τ in the low-pass filter by taking these factors into consideration.
As shown in Figure 9, when using multiple odd-numbered harmonics, the MPI signal at the center of the field-free region, i.e., ![]() was greater by a factor of approximately 2 compared to the case when only the third-harmonic signal was used, suggesting that the sensitivity of MPI can be increased by using multiple odd-numbered harmonics. Furthermore, when using multiple odd-numbered harmonics, the dent at
was greater by a factor of approximately 2 compared to the case when only the third-harmonic signal was used, suggesting that the sensitivity of MPI can be increased by using multiple odd-numbered harmonics. Furthermore, when using multiple odd-numbered harmonics, the dent at ![]() decreased, which was observed when only the third-harmonic signal was used. These findings appear to be advantageous in correcting for the system function in the spatial domain and/or for reducing artifacts induced by such a dent, because the system function in the spatial domain can be approximated by a smoothly-changing function such as the Gaussian function.
decreased, which was observed when only the third-harmonic signal was used. These findings appear to be advantageous in correcting for the system function in the spatial domain and/or for reducing artifacts induced by such a dent, because the system function in the spatial domain can be approximated by a smoothly-changing function such as the Gaussian function.
We used the first-order RC low-pass filter for extracting the DC component of the signal after mixing (Figure 1), because it is one of the simplest low-pass filters. The transfer function and unit step response of this filter are shown for various τ values in Figure 2(a) and Figure 2(b), respectively. When steeper roll-offs towards higher frequencies are desired, they can be achieved by cascading multiple first-order RC low-pass filters, i.e., the higher-order RC low-pass filter.
As previously described, we defined the MPI signal as the mean of ![]() [Equation (7)] and did not consider the phase [
[Equation (7)] and did not consider the phase [![]() in Equation (6)] in this study. Lock-in amplifiers are also used as phase-shift detectors [15] and
in Equation (6)] in this study. Lock-in amplifiers are also used as phase-shift detectors [15] and ![]() can be calculated from
can be calculated from
 (19)
(19)
where ![]() and
and ![]() denote the real and imaginary parts of
denote the real and imaginary parts of![]() , respectively. Actually,
, respectively. Actually, ![]() and
and ![]() are detected using phase shifters in lock-in amplifiers [15] . It may also be useful to investigate the dependency of
are detected using phase shifters in lock-in amplifiers [15] . It may also be useful to investigate the dependency of ![]() on the strength of the drive and selection magnetic fields and the particle size distribution of MNPs for analyzing the behavior of signal harmonics in MPI. Such a study is currently in progress.
on the strength of the drive and selection magnetic fields and the particle size distribution of MNPs for analyzing the behavior of signal harmonics in MPI. Such a study is currently in progress.
5. Conclusion
We presented a lock-in-amplifier model for analyzing the behavior of signal harmonics in MPI and some simulation results based on this model. This model will be useful for better understanding, optimizing, and developing MPI and for designing MNPs appropriate for MPI.
Acknowledgements
This work was supported by Grants-in-Aid for Scientific Research (Grant Nos.: 25282131 and 15K12508) from the Japan Society for the Promotion of Science (JSPS) and Japan Agency of Science and Technology (JST).