1. Introduction
Definition 1. For every coordinate system, there is no immediate reason for pre- ferring certain systems of co-ordinates to others.
Definition 2. I named 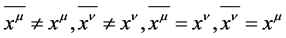 “Binary Law”.
“Binary Law”.
Definition 3. 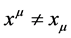 is established.
is established.
Definition 4. 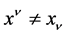 is established.
is established.
Definition 5. 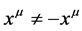 is established.
is established.
Definition 6. Convariant and contravariant tensor of the first rank 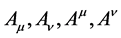 satisfied
satisfied  [1] .
[1] .
Definition 7. Tensor of rank zero 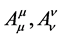 satisfied
satisfied 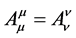 [1] .
[1] .
Definition 8. If tensor  satisfied
satisfied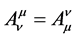 , this tensor
, this tensor  was named sym- metric tensor [1] .
was named sym- metric tensor [1] .
Definition 9. Convariant differentiation for Convariant Bector 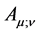 satisfied
satisfied 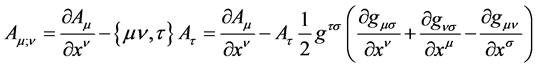 [1] .
[1] .
Definition 10. 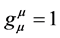 and
and ![]() are establishment [2] .
are establishment [2] .
Definition 11. Convariant differentiation for contravariant bector ![]() satisfied
satisfied ![]() [2] .
[2] .
Definition 12. Convariant differentiation for Scalar ![]() satisfied
satisfied ![]() [2] .
[2] .
2. About Reason to Take Binary Law into Consideration
We will have to receive existence of the absolute coordinate system if Definition 1 is not established. Therefore, we must accept establishment of Definition 1.
Proposition 1. Definition 1 is not established for all coordinate systems ![]()
Proof: All coordinate systems ![]() thinks about
thinks about ![]() in a standard and can divide it into two next groups.
in a standard and can divide it into two next groups.
![]()
![]() (1)
(1)
I think that I change the coordinate systems of the standard ![]() of (1) for all coordi- nate systems
of (1) for all coordi- nate systems ![]() sequentially now. By the way, the difference cannot occur between each conclusion to be provided here if Definition 1 is established. This reason is that all coordinate systems
sequentially now. By the way, the difference cannot occur between each conclusion to be provided here if Definition 1 is established. This reason is that all coordinate systems ![]() has a privilege of the equality each other if Definition 1 is established. At first (1) gets an invariable conclusion for
has a privilege of the equality each other if Definition 1 is established. At first (1) gets an invariable conclusion for ![]() exchange. Therefore, at least (1) must get an invariable conclusion for the next
exchange. Therefore, at least (1) must get an invariable conclusion for the next ![]() exchange if Definition 1 is established. Here, I get
exchange if Definition 1 is established. Here, I get
![]()
![]() (2)
(2)
by ![]() exchange from (1). Therefore, (2) must be equal with (1) if Definition 1 is established. By the way,
exchange from (1). Therefore, (2) must be equal with (1) if Definition 1 is established. By the way, ![]() of (1) is equal with
of (1) is equal with ![]() of (2), but
of (2), but ![]() of (1) is not equal with
of (1) is not equal with ![]() of (2). In other words, (2) is not equal with (1). Therefore, Definition 1 is not established for all coor- dinate systems
of (2). In other words, (2) is not equal with (1). Therefore, Definition 1 is not established for all coor- dinate systems![]() .
.
-End Proof
Establishment of Proposition 1 is a problem in thinking that Definition 1 must be established. Therefore, I aim at getting establishment of Definition 1 for all coordinate systems![]() .
.
Proposition 2. If all coordinate systems ![]() satisfies
satisfies ![]() , Definition 1 is established for all coordinate systems
, Definition 1 is established for all coordinate systems![]() .
.
Proof: I get
![]()
![]() (3)
(3)
![]()
![]() (4)
(4)
from (1), (2) if all coordinate systems ![]() satisfies
satisfies
![]() (5)
(5)
(3) is equal with (4) here. In other words, (2) is equal with (1) if all coordinate sys- tems ![]() satisfies (5). Therefore, Definition 1 is established for all coordi- nate systems
satisfies (5). Therefore, Definition 1 is established for all coordi- nate systems ![]() if all coordinate systems
if all coordinate systems ![]() satisfies (5).
satisfies (5).
-End Proof
Proposition 3. If all coordinate systems ![]() satisfies
satisfies ![]() , all coordinate systems
, all coordinate systems ![]() shifts to only two of
shifts to only two of ![]()
Proof: If all coordinate systems ![]() satisfies (5), I get
satisfies (5), I get ![]() than all coordinate systems
than all coordinate systems![]() .
.
-End Proof
Proposition 4. If ![]() is established,
is established, ![]() is esta- blished.
is esta- blished.
Proof: I get
![]() (6)
(6)
from (5), (7) if I assume establishment of
![]() (7)
(7)
when (5) is established. Because (6) includes contradiction,
![]() (8)
(8)
is established when (5) is established.
-End Proof
Proposition 5. If ![]() is established,
is established, ![]() are established.
are established.
Proof: When (5) is established, (8) is established from Proposition 4. Therefore, I get
![]() (9)
(9)
from (8), (10) if I assume establishment of ![]() when (5) is established. I can rewrite
when (5) is established. I can rewrite ![]() as
as
![]() (10)
(10)
here. When (5) is established, I get
![]() (11)
(11)
from Definition 3. Because (9) includes contradiction for (11),
![]() (12)
(12)
is established when (5) is established.
Similary, I get
![]() (13)
(13)
from (8), (14) if I assume establishment of ![]() when (5) is established. I can rewrite
when (5) is established. I can rewrite ![]() as
as
![]() (14)
(14)
here. When (5) is established, I get
![]() (15)
(15)
from Definition 4. Because (13) includes contradiction for (15),
![]() (16)
(16)
is established when (5) is established.
Similary, I get
![]() (17)
(17)
from (8), (18) if I assume establishment of ![]() when (5) is established. I can rewrite
when (5) is established. I can rewrite ![]() as
as
![]() (18)
(18)
here. When (5) is established, I get
![]() (19)
(19)
from Definition 5. Because (17) includes contradiction for (19),
![]() (20)
(20)
is established when (5) is established. And, I get
![]() (21)
(21)
from (12), (16), (20).
-End Proof
3. About the Tensor Which Satisfied Binary Law
We will have to think about adaptation of the establishment of Binary Law for the coordinate systems ![]() in the tensor if we think about establishment of Binary Law for all coordinate systems
in the tensor if we think about establishment of Binary Law for all coordinate systems![]() . Therefore, I decided to report Tensor when all coordinate systems
. Therefore, I decided to report Tensor when all coordinate systems ![]() satisfied Binary Law.
satisfied Binary Law.
Proposition 6. If all coordinate systems ![]() satisfied
satisfied ![]() , Convariant and Contravariant Tensor of the first rank does not change the form of the equation.
, Convariant and Contravariant Tensor of the first rank does not change the form of the equation.
Proof: I get
![]() (22)
(22)
from Definition 6 if all coordinate systems ![]() satisfies (5). Definition 6 and (22) are equal here. Therefore, if all coordinate systems
satisfies (5). Definition 6 and (22) are equal here. Therefore, if all coordinate systems ![]() satisfied (5), Convariant and Contravariant Tensor of the first rank does not change the form of the equation.
satisfied (5), Convariant and Contravariant Tensor of the first rank does not change the form of the equation.
-End Proof
Proposition 7. Tensor of the second rank becomes Symmetric Tensor if all coor- dinate systems ![]() satisfies
satisfies ![]()
Proof: I get
![]() (23)
(23)
from Definition 7 if all coordinate systems ![]() satisfies (5). Definition 7 and (23) are equal here. We can use (12), (16), (20), (21) for (23) by considering Pro- position 5 here. And we can rewrite (23) by using (12), (16) for
satisfies (5). Definition 7 and (23) are equal here. We can use (12), (16), (20), (21) for (23) by considering Pro- position 5 here. And we can rewrite (23) by using (12), (16) for
![]() (24)
(24)
Then, I get
![]() (25)
(25)
from (23),(24). And we can rewrite (23) by using (20), (21) for
![]() (26)
(26)
Then, I get
![]() (27)
(27)
from (26). Therefore, Tensor of the second rank becomes Symmetric Tensor than consideration of Definition 8 when all coordinate systems ![]() satisfies (5).
satisfies (5).
-End Proof
Proposition 8. If all coordinate systems ![]() satisfied
satisfied ![]() , The distance of two points be able to change oneself in connection with the metric of space.
, The distance of two points be able to change oneself in connection with the metric of space.
Proof: I get
![]() (28)
(28)
from Definition 10 if all coordinate systems ![]() satisfies (5). I get
satisfies (5). I get
![]()
![]() (29)
(29)
![]() (30)
(30)
![]() (31)
(31)
from Definition 9 if all coordinate systems ![]() satisfies (5). By the way, we cannot handle (30), (31) according to Proposition 3. We can use (12), (16), (20), (21) for (29) by considering Proposition 5 here. And we must rewrite (29) by using (16) for
satisfies (5). By the way, we cannot handle (30), (31) according to Proposition 3. We can use (12), (16), (20), (21) for (29) by considering Proposition 5 here. And we must rewrite (29) by using (16) for
![]() (32)
(32)
![]() (33)
(33)
I decide not to handle (33) by consideration of (28) here. Well, I get conclution from (32) that if all coordinate systems ![]() satisfied (5), Scalar quantity be able to change oneself in connection with the metric of space. Here, This Scalar quantity expressed the all of quantity expressed as Scalar. Therefore, I get conclution that the distance of two points be able to change oneself in connection with the metric of space.
satisfied (5), Scalar quantity be able to change oneself in connection with the metric of space. Here, This Scalar quantity expressed the all of quantity expressed as Scalar. Therefore, I get conclution that the distance of two points be able to change oneself in connection with the metric of space.
-End Proof
Proposition 9. If all coordinate systems ![]() satisfied
satisfied ![]() , convariant differentiation for Contravariant Bector
, convariant differentiation for Contravariant Bector ![]() behave like a convariant differentiation for Scalar
behave like a convariant differentiation for Scalar ![]()
Proof: I get
![]()
![]() (34)
(34)
![]() (35)
(35)
![]() (36)
(36)
from Definition 11 if all coordinate systems ![]() satisfies (5). By the way, we cannot handle (35), (36) according to Proposition 3. We can use (12), (16), (20), (21) for (34) by considering Proposition 5 here. And we must rewrite (34) by using (21) for
satisfies (5). By the way, we cannot handle (35), (36) according to Proposition 3. We can use (12), (16), (20), (21) for (34) by considering Proposition 5 here. And we must rewrite (34) by using (21) for
![]()
![]() (37)
(37)
And, I can get
![]() (38)
(38)
from (37) for consideration of (28). And we can rewrite (38) by using (21) for
![]() (39)
(39)
Because the second term of the right side of (38) does not exist here, we may adopt (38) and (39) description form of which. Well, I get conclution from (39), Definition 12 that if all coordinate systems ![]() satisfied (5), Convariant differentiation for Contravariant Bector
satisfied (5), Convariant differentiation for Contravariant Bector ![]() behave like a Convariant differentiation for Scalar
behave like a Convariant differentiation for Scalar![]() .
.
-End Proof
4. Discussion
About Definition 2:
I named (5) “Binary Law” by Proposition 3.
About Proposition 6:
Convariant and contravariant tensor of the first rank don’t change the formula whether it’s satisfied (5) or not.
About Proposition 8:
In (32), we can think that ![]() expressed the distance of two points in
expressed the distance of two points in ![]() is
is
establishment and this is constant. And, ![]() expresses the distance of two points in general and this is not constant.
expresses the distance of two points in general and this is not constant.
About Proposition 9:
In (39), we can handle ![]() as tensor similarly
as tensor similarly![]() .
.