Received 20 July 2016; accepted 22 August 2016; published 25 August 2016

1. Introduction
An Information Theory Radiation Model (ITRM) for radiation emitted by a black body passing through a scattering medium is analyzed. A variational method is used to derive three equations similar to the Black Body Radiation (BBR) law. But, these equations include the effect of scattering. In the limit when there is no scattering these models revert to the BBR law. The advantage of this mathematical model is that it includes the effect of the scattering of the radiation between source and detector. Three equations are derived. One equation describes the effect of the scattering on the radiation when the form of the scattering mechanism is known. The second result is an equation for the case when the forms of the scattering mechanisms are not known. In this case the model contains a single scattering parameter. The third equation is a simplified version of the case when the form of the scattering is not known. This is useful for the analysis of large data. The derivation of the case when the form of the scattering mechanism is not known is similar to one I presented in a previous publication [1] . It was formulated for the analysis of the Cosmic Background Radiation. A variational method using Information Theory was used to derive this model. To obtain the three equations the Information was maximized, subject to what is known about the system.
The basis of Information Theory was developed by C. E. Shannon [2] at Bell Laboratories. The information theoretical model facilitates the inclusion of the effect of information propagating through noisy channels [2] . Here the effect of the thermal radiation being scattered on the way from the hot Black Body source to the detector is analyzed.
One phenomenon to which one can apply this model is to the statistics of light quanta. In the Quantum Mechanical model of nature the energy of the electromagnetic radiation oscillating with any given frequency is divided into energy quanta or photons. The different quantum mechanical energy states are energy packets containing different numbers of photons. The information transmitted at any frequency by the hot body is encoded in the number of photons radiated. Different numbers of photons radiated represent different information, see Figure 1. Thus, an energy state represents an amount of information. The amount of information in each photon packet or energy state is not equal to the number of photons, but to a function of the number of photons. This is illustrated in Figure 1. The photon packets are represented by mail bags in Figure 1. The information in each mail bag is displayed on the tags. The unit of information used in this schematic representation is in binary bits. However, the information used in this article is in a unit of Joules per degree Kelvin.
The photons travel through space where some are absorbed or scattered. Maybe, the radiation when passing through an ionized cloud is even amplified by stimulated emission. This can occur by generating additional photons of the same frequency as the incoming radiation neutralizes some of the charges.
The model derived here can be used both when the details of the scattering mechanism is known and in a simple case when the details of the scattering mechanism is unknown. In the case when the scattering mechanism is known, the scattering mechanism is represented here by a stochastic model. It is represented by conditional probabilities that one number of photons were radiated provided another number of photons were received. The conditional probabilities have to be constructed to represent the known scattering model.
In the case when the detail forms of the scattering mechanisms are not known, the forms of the conditional probabilities can not be specified. In this case, the information formed by the conditional probabilities can be approximated by a function that includes a single average scattering parameter. Like the BBR, the ITRM depends on the absolute temperature.
In the case when the radiation data is known, the source temperature and the average scattering parameter can be determined by comparing the data to calculated ITRM values. This is the case, for example, for the Cosmic Microwave Background radiation.
One result of including the effect of scattering is a blue shift of the distribution of photons, see Figure 2. Unlike in the case of the Doppler effect the wavelength of the individual photons do not change. However, the distribution changes to more short wave photons. The total number of photons can also change to fewer or more photons.
![]()
Figure 1. Schematic representation of the encoding of the information. The information is encoded in the number of photons transmitted. The amount of information in each photon packet is a function of the number of photons in the packet. The photon packets are represented by mail bags here. The information in each mail bag is displayed on its tag.
![]()
Figure 2. Schematic representation of a blue shifted photon distribution. Unlike in the case of the Doppler effect, the wavelength of the individual photons do not change. However, the distribution changes to more short wave photons.
2. Information Model
The ITRM for thermal radiation through a scattering medium is derived below. Some of the derivation is similar to the derivation in my Cosmic Background Radiation analysis paper [1] . The concepts used here can be found in a paper by C. E. Shannon [2] and many Probability texts [3] - [5] . The information is encoded in the number n of photons radiated by the hot object, see Figure 1. The value of the information gn in each information packet is a function of the number n of photons.
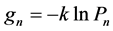 (2.1)
(2.1)
where k is Boltzmann constant and Pn is the probability that a signal of n photons is being received. This is similar to the famous Boltzmann equation engraved on his tombstone. The equation on the tombstone is for uniform
probabilities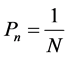 . The information here is in a unit of Joules per degree Kelvin. Note that the probabilities
. The information here is in a unit of Joules per degree Kelvin. Note that the probabilities
Pn are less or equal to one. Therefore, the logarithm of the probability is negative and the information gn is positive. The information packets are shown schematically as mail bags in Figure 1. The probabilities Pn are normalized.
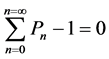 (2.2)
(2.2)
The average detected Shannon information is equal to the average value H of all the information packets.
 (2.3)
(2.3)
The propagation of the photons from the hot Black Body source to the detector is modeled by conditional probabilities P (m photons radiated | provided n Photons received) that m photons are radiated provided n photons were received. Associated with the conditional probabilities having the same condition of n photons being received are conditional entropies h(S|n). Here S is the set of all the different numbers m of radiated photons and n is the number of photons that were received [5] .
 (2.4)
(2.4)
Here k is Boltzmann constant and n is the number of photons that were received. The average value N of the conditional information is also known as the noise:
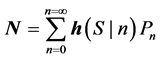 (2.5)
(2.5)
The information I is equal to the difference between the received Shannon information H of Equation (2.3) and the noise N of Equation (2.5)
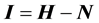 (2.6)
(2.6)
The temperature T is the change of the light energy U with the information H carried by the photons. For this derivation the temperature T of the radiation at the receiver is assumed to be known.
 (2.7)
(2.7)
where the average energy U of the received photons is given by:
 (2.8)
(2.8)
Its value, at this point, is not known. Here h is Plank’s constant divided by 2π and ω is the oscillating frequency of the radiation.
A variational method is used to calculate the values of the Probabilities Pn. The probabilities Pn can be derived by finding an extremum value of the information I subject to what is known about the system. In this case the temperature T at the receiver and the fact that the probabilities are normalized are known about the system. However, the Equation (2.7) for the temperature, is not in the form of a constraint equation like Equations (2.2) and (2.8). Therefore, it can not be used in this process directly. Instead one has to use the average energy U first. By multiplying the two constraint equations, Equations (2.2) and (2.8) by convenient constants  and adding them to the equation for the information I one obtains:
and adding them to the equation for the information I one obtains:
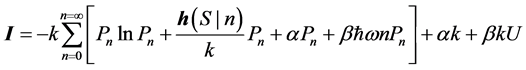 (2.9)
(2.9)
The information I will have an extremum value when all its derivatives with respect to the probabilities Pn are equal to zero. By taking the derivative of the information I with respect to one of the probabilities Pn, setting the result equal to zero and solving for the probability Pn one obtains:
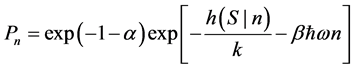 (2.10)
(2.10)
The values of the constants α and β are not known at this point. In order to evaluate the constant α one substitutes the probability of Equation (2.10) into the first constraint equation, which is Equation (2.2). One obtains for :
:
![]() (2.11)
(2.11)
The constant α can be eliminated by substituting Equation (2.11) into Equation (2.10).
![]() (2.12)
(2.12)
The constant β has yet to be evaluated. In order to accomplish this, one must first calculate the information ![]() of receiving n photons by taking the logarithm of the probability
of receiving n photons by taking the logarithm of the probability ![]() of Equation (2.12) and multiplying the result by minus the Boltzmann constant.
of Equation (2.12) and multiplying the result by minus the Boltzmann constant.
![]() (2.13)
(2.13)
By substituting the information associated with receiving n photons, Equation (2.13), into the average Shannon information of Equation (2.3) one obtains:
![]() (2.14)
(2.14)
where Equation (2.8) was used for the average energy U. By solving Equation (2.14) for the average energy U, substituting the resulting expression into Equation (2.7) and solving for β one obtains the well known expression:
![]() (2.15)
(2.15)
The probability Pn of receiving n photons can now be completely specified by substituting Equation (2.15) for the constant β into Equation (2.12).
![]() (2.16)
(2.16)
The average energy of a one dimensional radiating system where the radiation passes through a scattering medium is derived by substituting the probabilities of Equation (2.16) into the equation for the average received energy U, Equation (2.8).
![]() (2.17)
(2.17)
where the normalized frequency x is given by:
![]() (2.18)
(2.18)
Finally, by multiplying Equation (2.17) by an appropriate density of states constant one obtains for the change
![]() of the average received energy density u with radiation frequency ω of a three dimensional system radiating through a scattering medium:
of the average received energy density u with radiation frequency ω of a three dimensional system radiating through a scattering medium:
![]() (2.19)
(2.19)
where h(S|n) is given by Equation (2.4) and where c is the speed of light in free space. This is the first result. It is the Black Body Radiation law for systems radiating through a scattering medium. It can be used when the form of the conditional probabilities that describe the scattering mechanism are known. Note that the temperature T is the observed temperature at the receiver. For the case when there is no scattering, when h(S|n) is equal to zero, Equation (2.19) reverts to the standard Black Body Radiation law.
![]() (2.20)
(2.20)
For the case when the details of the scattering models are not known the conditional probabilities can not be specified. However, one can postulate a simple model for the conditional information or conditional entropies [3] [4] h(S|n).
![]() (2.21)
(2.21)
where ρ is an average scattering parameter. By substituting Equation (2.21) into Equation (2.19) one obtains for
the change ![]() of the average received energy density u with radiation frequency ω for the case when the scattering mechanisms are not known:
of the average received energy density u with radiation frequency ω for the case when the scattering mechanisms are not known:
![]() (2.22)
(2.22)
and where![]() . Since the scattering parameter ρ is an Entropy Amplitude it must always be positive. This is the second result. This result was also used in my Cosmic Background Radiation analysis paper [1] . It is applicable when the form of the scattering mechanism is not known. It describes the scattering process in terms of a single scattering parameter ρ. This shifts the peak of the distribution to larger values of the normalized
. Since the scattering parameter ρ is an Entropy Amplitude it must always be positive. This is the second result. This result was also used in my Cosmic Background Radiation analysis paper [1] . It is applicable when the form of the scattering mechanism is not known. It describes the scattering process in terms of a single scattering parameter ρ. This shifts the peak of the distribution to larger values of the normalized
frequency ![]() see Figure 2.
see Figure 2.
Equation (2.22) can be expressed as follows for large values of![]() :
:
![]() (2.23)
(2.23)
where
![]() (2.24)
(2.24)
Equation 2.23 is the third result. This equation is especially useful when large data is to be analyzed.
For completeness, the input information I is calculated by subtracting the noise N from the Shannon information H of Equation (2.3). The noise N is calculated in Equation (2.5). Equation (2.16) is used for the probabilities Pn.
![]() (2.25)
(2.25)
Note that the first and last terms of Equation (2.25) cancel. By making use of Equation (2.17) for the average energy U one obtains:
![]() (2.26)
(2.26)
By multiplying Equation (2.26) by the same density of states as was used in Equation (2.19) one obtains:
![]() (2.27)
(2.27)
Equation (2.27) is in![]() . The explanation given here of the shift of the photon distribution to higher frequencies is due to the effect of the scattering process as discussed above.
. The explanation given here of the shift of the photon distribution to higher frequencies is due to the effect of the scattering process as discussed above.
3. Conclusion
An Information Theory Radiation Model (ITRM) for radiation passing through a scattering medium radiated by a black body has been derived. The result of this analysis is given by Equations (2.19), (2.22) and (2.23). Equation (2.19) is the ITRM for the case when the conditional probabilities that describe the scattering mechanisms are known. Equation 2.22 is an approximation of the ITRM for the case when the form of the scattering mechanisms is not known. In this case a single average scattering parameter is used to characterize the scattering process. Equation (2.23) is an approximation of Equation (2.22). It is an equation for the case when the form of the scattering mechanisms are not known. It has a simpler form than Equation (2.22), but it is only valid for large
values of![]() . This equation is especially useful when large sets of data are analyzed. In the limit of no scatter-
. This equation is especially useful when large sets of data are analyzed. In the limit of no scatter-
ing the ITRM reverts to the Black Body Radiation law.