Existence of Positive Solutions to Semipositone Fractional Differential Equations ()
Received 19 June 2016; accepted 14 August 2016; published 17 August 2016

1. Introduction
The aim of this paper is to investigate the existence of positive solutions to the semipositone fractional differential equation
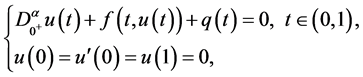 (1)
(1)
where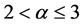 ,
,  is the standard Riemann-Liouville fractional derivative of order
is the standard Riemann-Liouville fractional derivative of order  which is defined as follows:
which is defined as follows:
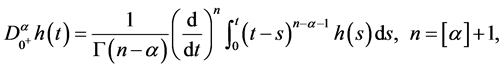
where 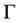 denotes the Euler gamma function and
denotes the Euler gamma function and  denotes the integer part of number
denotes the integer part of number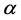 , provided that the right side is pointwise defined on
, provided that the right side is pointwise defined on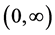 , see [1] . Here, by a positive solution to the problem (1), we mean a function
, see [1] . Here, by a positive solution to the problem (1), we mean a function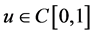 , which is positive in
, which is positive in , and satisfies (1).
, and satisfies (1).
Fractional differential equations have gained much importance and attention due to the fact that they have been proved to be valuable tools in the modelling of many phenomena in engineering and sciences such as physics, mechanics, economics and biology. In recent years, there exist a great deal of researches on the existence and/or uniqueness of solutions (or positive solutions) to boundary value problems for fractional-order differential equations. Sun [2] studied the existence of positive solutions for the following boundary value pro- blems:

where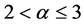 ,
,  is continuous and
is continuous and 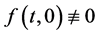 on
on![]() . But paper [2] did not give the results of the existence of positive solution when the nonlinearity can take negative value, i.e. semipositone problems.
. But paper [2] did not give the results of the existence of positive solution when the nonlinearity can take negative value, i.e. semipositone problems.
The purpose of the present paper is to apply the method of varying translation together with the fixed point theorems in cone to discuss (1) without nonnegativity imposed on the nonlinearity. Meanwhile, we also allow the nonlinearity to have many finite singularities on![]() .
.
2. Preliminaries and Lemmas
In this section, we present several lemmas that are useful to the proof of our main results. For the forthcoming analysis, we need the following assumptions:
(H1) ![]() is continuous. For any
is continuous. For any![]() , there exist constants
, there exist constants ![]()
such that ![]()
(H2) ![]() with
with ![]() and
and![]() ,
,
![]() where
where ![]()
![]()
![]() will be defined in the following text.
will be defined in the following text.
In [3] , the authors obtained the Green function associated with the problem (1). More precisely, the authors proved the following lemma.
Lemma 2.1 [3] . For any![]() , the unique solution of the boundary value problem
, the unique solution of the boundary value problem
![]() (2)
(2)
is given by
![]() (3)
(3)
where
![]() (4)
(4)
Lemma 2.2 [4] . The Green function ![]() defined by (4) satisfies the inequality
defined by (4) satisfies the inequality
![]() (5)
(5)
here
![]()
Remark 2.1. A simple computation shows that there exists a constant ![]() such that
such that
![]()
Remark 2.2 [5] . If ![]() satisfies (H1), then for any
satisfies (H1), then for any ![]()
![]() is increasing on
is increasing on ![]()
and for any![]() ,
, ![]()
Lemma 2.3 [6] . Let X be a real Banach space, ![]() be a bounded open subset of X with
be a bounded open subset of X with ![]() and
and ![]() is a completely continuous operator, where P is a cone in X.
is a completely continuous operator, where P is a cone in X.
(i) Suppose that ![]() then
then![]() .
.
(ii) Suppose that ![]() then
then![]() .
.
Consider the Banach space ![]() with the usual supremum norm
with the usual supremum norm ![]() and define the
and define the
cone![]() . Let
. Let![]() , then
, then ![]() is the unique solution
is the unique solution
to (2) for![]() . Now we first consider the singular nonlinear boundary value problem
. Now we first consider the singular nonlinear boundary value problem
![]() (6)
(6)
where ![]() We have the following Lemma.
We have the following Lemma.
Lemma 2.4. If the singular nonlinear boundary value problem (2) has a positive solution ![]() such that
such that ![]() for any
for any![]() . Then boundary value problem (1) has a positive solution
. Then boundary value problem (1) has a positive solution![]() .
.
Proof. In fact, if u is a positive solution to (6) such that ![]() for any
for any![]() . Let
. Let![]() , then
, then![]() . Since
. Since ![]() is the unique solution to (2) for
is the unique solution to (2) for ![]() for any
for any![]() , we
, we
have![]() , which implies that
, which implies that![]() . So
. So
![]() . Consequently
. Consequently ![]() is positive solution to (1). This complete the proof of Lemma 2.4.
is positive solution to (1). This complete the proof of Lemma 2.4.
For any![]() , define an operator
, define an operator
![]() (7)
(7)
Since for any fixed![]() , we can choose
, we can choose ![]() such that
such that![]() . Note that
. Note that
![]() so by (H1), we have
so by (H1), we have
![]()
Consequently, for any![]() , we have
, we have
![]() (8)
(8)
Therefore, the operator T is well defined and ![]()
Lemma 2.5. Assume that (H1), (H2) hold. Then ![]() is a completely continuous operator.
is a completely continuous operator.
Proof. For any![]() , in view of (2) we conclude that
, in view of (2) we conclude that
![]()
Whence, it follows from (8) that ![]() which implies
which implies ![]()
Next we show that ![]() is continuous. Suppose
is continuous. Suppose![]() , and
, and ![]() Then, there exists a constant
Then, there exists a constant ![]() such that
such that![]() . Since for any
. Since for any ![]()
![]() , by Remark 2.2, we have
, by Remark 2.2, we have
![]() (9)
(9)
Thus, we have
![]()
and![]() . It follows from the Lebesgue control convergence theorem that
. It follows from the Lebesgue control convergence theorem that
![]()
which implies ![]() is continuous.
is continuous.
In what follows, we need to prove that ![]() is relatively compact.
is relatively compact.
Let ![]() be any bounded set. Then there exists a constant
be any bounded set. Then there exists a constant ![]() such that
such that ![]() for any
for any![]() . Similarly as (9), for any
. Similarly as (9), for any ![]() we have
we have
![]() (10)
(10)
Consequently
![]() (11)
(11)
Therefore ![]() is uniformly bounded.
is uniformly bounded.
Now we show that ![]() is equicontinuous on
is equicontinuous on![]() . For any
. For any![]() , by (9), (11) and the Lebesgue control convergence theorem, and noticing the continuity of
, by (9), (11) and the Lebesgue control convergence theorem, and noticing the continuity of![]() , we have
, we have
![]() (12)
(12)
Thus, ![]() is equicontinuous on [0,1]. The Arezlà-Ascoli Theorem guarantees that
is equicontinuous on [0,1]. The Arezlà-Ascoli Theorem guarantees that ![]() is relatively compact set. Therefore
is relatively compact set. Therefore ![]() is completely continuous operator.
is completely continuous operator.
Lemma 2.6. Let ![]() then
then![]() .
.
Proof. Assume that there exists ![]() such that
such that ![]() Then
Then ![]() and
and ![]() Thus we have
Thus we have
![]()
This contradiction shows that![]() .
.
Lemma 2.7. There exists a constant ![]() such that
such that![]() , where
, where ![]()
Proof. Choose constants ![]() and N such that
and N such that
![]()
From Remark (2.2), there exists![]() , such that
, such that
![]() (13)
(13)
Let ![]() Obviously,
Obviously, ![]() Now we show that
Now we show that ![]() In
In
fact, otherwise, there exists ![]() such that
such that ![]() By (2), for any
By (2), for any ![]() we have
we have
![]()
So
![]()
Consequently, ![]() That is
That is ![]() This
This
contradiction shows that![]() .
.
3. Main Results
Theorem 3.1. Suppose that (H1), (H2) hold. Then, the boundary value problems (1) has at least one positive solution![]() , and exists a constant
, and exists a constant ![]() such that
such that ![]()
Proof of Theorem 3.1. Applying Lemma 2.6 and Lemma 2.7 and the definition of the fixed point index, we have ![]() Thus T has a fixed point
Thus T has a fixed point ![]() in
in ![]() with
with![]() . Since
. Since![]() , we have
, we have
![]()
Let ![]() It follows from Lemma (2.4) that
It follows from Lemma (2.4) that ![]() is a positive solution to boundary value problem (1), and there exists a constant
is a positive solution to boundary value problem (1), and there exists a constant ![]() such that
such that ![]()
Acknowledgements
We thank the Editor and the referee for their comments. This research was supported financially by the National Natural Science Foundation of China (11471187, 11571197), the Natural Science Foundation of Shandong Province of China (ZR2014AL004) and the Project of Shandong Province Higher Educational Science and Technology Program (J14LI08), the Project of Scientific and Technological of Qufu Normal University (XKJ201303).