ANFIS Based Space Vector Modulation-DTC for Switched Reluctance Motor Drive ()
Received 11 April 2016; accepted 17 May 2016; published 12 August 2016

1. Introduction
Switched reluctance motor, the doubly salient, separately energized motor has basic and simple construction. In spite of the fact that, the induction motor is still the good horse of the industries, the promising component of the high torque to inertia ratio, high torque to mass ratio, less maintenance and incredible general execution of SRM make it an effective contender for alternating current drives. The simple converter topology and dynamic algorithm because of the unipolar operation staying away from shoot through deficiencies makes SRM invaluable in utilizations of aviation, which require high unwavering quality. Additionally, it finds wide application in commercial car enterprises, direct drive machine apparatuses and so forth [1] .
In any case, huge torque ripple, vibration and acoustic noise are the principle disadvantages of SRM to accomplish superior. As the control of SRM is being the late pattern of research, plans were created including linear and non-linear models to control torque ripple [2] . Be that as it may, because of incorrectness in linear models and unpredictability included in non-linear control, the Direct Torque Control (DTC) was proposed which gave basic answer for control the motor torque and speed and minimized torque ripple.
The direct torque control strategies were proposed amidst the 1980’s for induction motor [3] [4] . The essential thought of DTC is slip control which depends on the unique relationship between the torque and slip. Contrasted as field orientated control, the DTC has numerous points of interest, for example, less machine parameter reliance, basic construction and quick dynamic torque reaction [5] [6] . Need for current controller in eliminated in DTC, in light of the fact that it chooses the voltage space vectors as indicated by the errors of flux linkage and torque. The switching conditions of the inverter are modified in every sampling time. Inside every inspecting interim, inverter keeps the state until the output conditions of the hysteresis controller change. Consequently, the frequency of switching is normally altered; it changes with the rotor speed, connected load and bandwidth of the flux and torque controllers. Despite the fact that DTC is getting more mainstream, it likewise has a few downsides, for example, the torque ripple and flux ripple. Numerous researchers have paid consideration on this issue at this point and proposed answers for it. To expand the quantity of vectors to be connected to the machine, Takahashi proposed a double three stage inverter [7] and C.G. Mei utilized variable switching sectors to minimize the torque and flux ripple [8] . Nonetheless, the researchers are not completely fulfilled and the effort to decrease the torque ripple and flux ripple is proceeding.
In traditional DTC, one of the 6 magnitude vectors of 33 combinations is controlled flux and torque inside the breaking points of hysteresis limits. Likewise in traditional DTC the ON/OFF of SRM converter switches are controlled by the error in torque and flux however extensive and little mistakes are not recognized. The exchanging vectors had picked same for expansive and little blunders. Keeping in mind the end goal to defeat this issue, SVM-DTC techniques were presented. Space vector modulation (SVM) modulator is joined with direct torque control for prompting engine drives as appeared in [9] - [11] to give a consistent inverter switching frequency. Noticing that the torque ripple and acoustic noise issue for this SVM-based DTC methodology are essentially enhanced for invoking zero inverter switching state inside each switching time of inverter control.
Later with the advancement of evolutionary control and its research the objective complexity and the complexity of control target are simplified. A spurt of action in the evolutionary control strategies including ANN system and fuzzy control discovered application in SRM drive control. Evolutionary strategies like fuzzy were created [12] [13] which were model free. In [14] - [17] the DTC has likewise been utilized with “feed-forward neural networks” keeping in mind the end goal to substitute for the ideal switching table to accomplish better execution with high dependability.
In this paper shows, the control algorithm executed is the hybrid of fuzzy control and neural system with the SVM-DTC for SRM drive. Controllers in view of direct torque control don’t require complex transformations. The simple neural-fuzzy structure recommended here is additionally straightforward, thus the general closed loop structure acquired is not complex. The Sugeno Neuro-fuzzy framework approximate complicated functions using several layers of neurons, organized similarly as the human cerebrum. At each sampling time the voltage vector selection picks the inverter switching state which diminishes the instantaneous flux and torque errors.
2. Integrated Neuro-Fuzzy Controller
The integration of neural networks and fuzzy inference system could be formatted into three main categories:
・ cooperative neuro-fuzzy models―fuzzy associative memories
・ concurrent neuro-fuzzy models―fuzzy rules extraction using self-organizing maps
・ Integrated neuro-fuzzy models―systems capable of learning fuzzy set parameters.
Mamdani method, Takagi-Sugeno method and hybrid neuro-fuzzy systems were supplementary introduced based on the outstanding features and advantages of the different types of integrated neuro-fuzzy models. The parameters of fuzzy inference systems are determine using, neural network learning algorithms in case of hybrid model. Integrated neuro-fuzzy systems share data structures and knowledge representations. A fuzzy system can make use of human knowledge by recording its vital components in law base and database, and carry out fuzzy analysis to compute the overall output value. The derivation of if-then rules and equivalent membership functions depends mainly on the a priori information about the system under consideration.
A typical approach to apply a learning algorithm to a fuzzy system is representing it in a special neural network like architecture. However the typical neural system inclining calculations (angle plunge) can’t be connected specifically to such a framework as the capacities utilized as a part of the deduction procedure are normally non differentiable function. This paper utilizes a coordinated Neuro-Fuzzy framework executing Sugeno Fuzzy Inference System as appeared in Figure 1.
3. Takagi-Sugeno Integrated Neuro-Fuzzy System
Takagi-Sugeno Neuro-Fuzzy frameworks make utilization of a blend of back propagation to take in the membership functions and minimum mean square estimation to decide the coefficients of the linear combinations in the standard’s decisions. A stage in the learning strategy got two sections: In the main part the info examples are spread, and the ideal conclusion parameters are assessed by an iterative least mean square system, while the precursor parameters (Member function) are thought to be settled for the present cycle through the proper training set. In the second part the examples are engendered once more, and in this age, back propagation is utilized to alter the forerunner parameters, while the conclusion parameters stay ideal. This strategy is then iterated n number of times. The elaborated and clear working of every layer (portrayed in Figure 2) is as per the following 6 layer.
Layer 1 (Input Layer) No calculation is done in this layer. Every node in this layer, which compares to one information variable, just transmits input qualities to the following layer straightforwardly. The connection
![]()
Figure 2. Takagi sugeno neuro-fuzzy system.
weight in layer 1 is solidarity.
Layer 2 (Fuzzification layer) Every node in this layer compares to one phonetic name (PE, ZE, NE…) to one of the information variables in layer 1. As it were, the output link represents the membership value, which determines the extent to which an info esteem has a place with a fuzzy set and is figured in layer 2. A bunching calculation will choose the underlying number and sort of membership functions to be designated to each of the info variable. The last states of the MFs will be calibrated amid system learning
Layer 3 (Rule Antecedent Layer) A node in this layer speaks to the precursor part of a standard. Generally a T-standard operator is utilized as a part of this hub. The yield of layer 3 node highlights the terminating quality of the comparing fuzzy guideline)
Layer 4 (Rule Strength Normalization) Each node in this layer figures the proportion of the ith principle’s quality to the aggregate of all guidelines terminating quality the Figure 2. Demonstrates the design of Takagi- Sugeno Neuro-fluffy frameworks
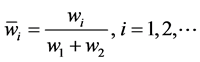 (1)
(1)
Layer 5 (Rule Consequent Layer) Every node I in this layer is represented with a node function
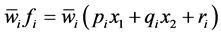 (2)
(2)
where 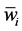 is the output of layer 4, and {pi, qi, ri} is the parameter set. A fine established way is to find the consequent parameters viva the least mean squares algorithm.
is the output of layer 4, and {pi, qi, ri} is the parameter set. A fine established way is to find the consequent parameters viva the least mean squares algorithm.
Layer 6 (rule inference layer) The single node in this layer computes the overall output as the addition of all input signals.
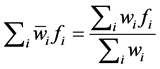 (3)
(3)
4. Proposed Takagi-Sugeno Integrated Neuro-Fuzzy System
Fuzzy logic and neural systems are corresponding advances in the outline of intelligent frameworks. Simulated neural systems (ANN) are low-level computational calculations that offer great execution with tangible information, while fuzzy logic manages thinking in a larger amount than ANN. The proposed framework utilizes Sugeno neuro-fuzzy framework, an Adaptive NF Inference System (ANFIS) for voltage space-vector era. It relates fuzzy logic and simulated neural systems for decoupled flux and torque control. As appeared in Figure 3. The error signs are conveyed to the NF controller, which is additionally entered by the real position of the stator flux vector. The NF controller decides the stator voltage order vector in polar directions for the SVM square. The plan is described by a basic self-tuning strategy and great steady-state and dynamic execution. This framework has two inputs―torque inaccuracy, flux inaccuracy which are got as the distinction between the reference number and actual number.
Takagi-Sugeno Neuro-Fuzzy frameworks make utilization of a blend of back propagation to take in the membership functions and slightest mean square estimation to decide the coefficients of the linear combinations in the tenet’s decisions. A stage in the learning system got two sections: The main part the information examples are proliferated, and the ideal conclusion parameters are evaluated by an iterative minimum mean square methodology, while the precursor parameters are thought to be altered for the present go through the preparation set.
In the second part the examples are propagated once more, and in this age, back proliferation is utilized to alter the predecessor parameters, while the conclusion parameters stay settled. This strategy is then iterated. The flux error (Fe) utilize three semantic qualities: positive error (PE), zero error (ZE) and negative error (NE) with universe of talk [−0.01, 0.01]. For the torque error(Te) the universe of talk is [−0.1, 0.1] with three fluffy totals positive (P), negative (N) and zero(Z).The point by point working of every layer (as delineated in) is as per the following.
Here Ii, Ij, Ik, Il represents the inputs to the neuron and Oi, Oj, Ok, Ol represents the yield of the neurons in layers 1, 2, 3 and 4 separately.
First layer: In the first layer of the NF structure, flux error and torque error are multiplied by respective weights and are each mapped through three fuzzy logic triangular membership functions
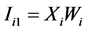 (4)
(4)
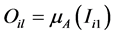 (5)
(5)
Second layer: This layer calculates the minimum value of the inputs
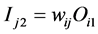 (6)
(6)
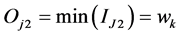 (7)
(7)
Third layer: This layer normalizes each input with respect to the others. The kth node output is the kth input divided by the sum of all the other inputs.
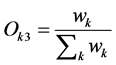 (8)
(8)
Fourth layer: This layer output is a linear function of the input and the ANFIS signals. The weight 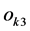 is the weight of both the incremental angle and the amplitude of desired reference voltage vector, so that:
is the weight of both the incremental angle and the amplitude of desired reference voltage vector, so that:
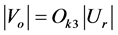 (9)
(9)
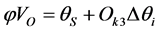 (10)
(10)
where, ![]() is the amplitude of desired reference voltage,
is the amplitude of desired reference voltage, ![]() is the maximum reference voltage amplitude,
is the maximum reference voltage amplitude, ![]() is the angle of the desired reference voltage,
is the angle of the desired reference voltage, ![]() is the incremental angle and
is the incremental angle and ![]() is the actual angle of the stator flux vector.
is the actual angle of the stator flux vector.
Fifth layer: This layer sums all the incoming signals
![]() (11)
(11)
The parts of the required reference voltage vector are added to each other, which is conveyed to the space vector modulator which figures the switching state of the converter. The system is tuned by minimum square estimation for yield enrolment work and back propagation calculation for output and input membership function.
5. Simulation Result
A Matlab/Simulink shut circle model was developed for the SRM and Sugeno sort mixture neuro-fuzzy control framework as in Figure 4. The engine parameters, for example, torque, stage flux and position are determined from the 3φ SRM.
Versatile Neuro-Fuzzy Inference System (ANFIS) for voltage space vector era is built. This controller joins fuzzy logic and Artificial Neural Network (ANN) with DTC for decoupled flux and torque control. The torque and flux inaccuracy are created taking into account the distinction among the reference and actual estimations of torque and stator flux individually. Inspected flux and torque inaccuracy, duplicated by weights, are conveyed to the three member function capacities in both inputs. In view of the present position of engine, torque inaccuracy and flux error the ideal determination of voltage space vector is finished with the assistance of ANFIS controller. Accordingly the converter switches and consequently the engine is controlled by DTC plan.
In this simulation test, the engine reference flux and torque were kept up at a consistent of 0.3 Wb and 5 Nm separately. The individual flux linkages prompts smooth consistent amplitude flux vector in the stator air hole. The torque results in Figures 5-7 indicates lower swell substance and consistent sufficiency nature. It is seen
![]()
Figure 4. Simulation diagram of ANFIS based SVM-DTC controller.
![]()
Figure 5. Torque developed in conventional DTC.
![]()
Figure 6. Torque developed in sugeno neuro-fuzzy controller.
![]()
Figure 7. Reduced torque errors due to training.
obviously from the range examination that in enduring state the neuro-fuzzy based DTC prompts lower swell and henceforth better execution.
The quantity of epochs was 100 for training. The quantity of MFs for the info variables Te and Fe is 3 and 3, respectively. The quantity of rules is then 9. The triangular MF is utilized for the two info variables. Obviously the triangular MF is indicated by two parameters. Along these lines, the ANFIS utilized here contains a sum of 39 fitting parameters, of which 12 (3 × 2 + 3 × 2 = 12) are the reason parameters and 27 (3 × 9 = 27) are the subsequent parameters. The preparation and testing root mean square (RMS) error got from the ANFIS are 4.7 ´ 10−6 and 5.3 ´ 10−6 respectively.
6. Conclusions
The proposed work delivers high accurate selection of voltage space vector and also illustrated the great potential of using the intelligent structures especially when working with a highly non-linear system. The speciality of using ANFIS is achieving fast torque response and no flux dropping caused by sector changes. The simulation shows that despite of their simple control structure the proposed ANFIS had managed to significantly reduce the torque and flux ripples. In addition it also gives good flux dynamics with low sampling time. The advantages of the proposed ANFIS based SVM-DTC are:
・ Constant switching frequency;
・ Very low torque and current distortion;
・ No sector change distortion and lower sampling time;
・ Very fast torque and flux response.