Optimal Dynamic Proportional and Excess of Loss Reinsurance under Dependent Risks ()
Received 11 May 2016; accepted 12 June 2016; published 15 June 2016

1. Introduction
In the last two decades the optimal reinsurance problem has had an important impact in the actuarial literature. Several authors have studied this problem with different purposes and referring to different surplus processes. Starting from the classical model where the process of the total claim amount has a Poisson compound distribution or follows a diffusion process, the adjustment coefficient, or the expected utility of the terminal wealth are been optimized (see, for example, [1] and [2] ).
With similar optimization aims, a more realistic model has been often considered, with two or more dependent classes of insurance business. Similar approaches are, for example: in [3] where the excess of loss insurance is considered and the adjustment coefficient or the expected utility of the terminal wealth are maximized, in [4] and in [5] where the expected utility of the terminal weal this maximized, in [6] where the adjustment coeffi- cient is maximized. This paper considers two classes of insurance business, dependent through the number of claims, and considers the proportional and the excess of loss reinsurances. The paper is organized as follows: in Section 2 the assumptions and the model are explained, in Sections 3 and 4, the problem is presented; subsequently the Hamilton-Jacobi-Bellman (HJB) equation is given and discussed in some particular cases. In Section 5, the problem with the only excess of loss reinsurance is solved; the optimal strategy and the corresponding value function are obtained.
2. The Model
We consider the finite time horizon 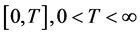 and a model in which two dependent risks are involved. In particular, we assume two classes of insurance business, being the claim number processes correlated. The arrival claim processes are
and a model in which two dependent risks are involved. In particular, we assume two classes of insurance business, being the claim number processes correlated. The arrival claim processes are  we assume that these processes are Poisson processes defined as follows:
we assume that these processes are Poisson processes defined as follows:
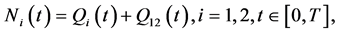 (1)
(1)
where Q1, Q2 and Q12 are Poisson random variables with positive parameters θ1, θ2 and θ12 respectively.
We furthermore assume that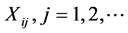 , are the random variables claim size of the risks
, are the random variables claim size of the risks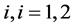 , where we assume that X1j and X2j have the same distribution functions F1 and F2 with Fi (x) = 0, for x ≤ 0, and expected value
, where we assume that X1j and X2j have the same distribution functions F1 and F2 with Fi (x) = 0, for x ≤ 0, and expected value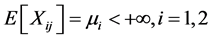 . We also assume that the moment generating functions:
. We also assume that the moment generating functions:
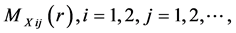
exist. As usually stated, the random variables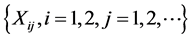 , are mutually independent, and independent of
, are mutually independent, and independent of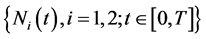 .
.
Let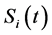 ,
, 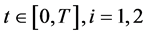 , the aggregate claims amounts for the two classes of insurance risk. Because of the made assumptions, the process
, the aggregate claims amounts for the two classes of insurance risk. Because of the made assumptions, the process , has a bivariate Poisson distribution and
, has a bivariate Poisson distribution and 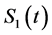 and
and 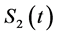 are correlated by θ12 resulting:
are correlated by θ12 resulting:
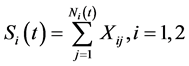 (2)
(2)
We consider the random variables![]() , identically distributed to
, identically distributed to ![]() respectively. We
respectively. We
assume that the random variables Xi are upper limited or that ![]()
We denote by ![]() the premium rate, calculated by the expected value principle, including a safety loading coefficient
the premium rate, calculated by the expected value principle, including a safety loading coefficient![]() :
:
![]() (3)
(3)
We assume that the principal insurer can implement both a proportional and an excess of loss reinsurance referred to both classes of insurance risks, with the respective retention levels ![]() for the proportional reinsurance, and retention limits
for the proportional reinsurance, and retention limits ![]() for the excess of loss reinsurance.
for the excess of loss reinsurance.
We therefore denote by ![]() any admissible control strategy that, for simplicity, we denote by
any admissible control strategy that, for simplicity, we denote by ![]()
The reinsurer, because of the proportional reinsurance, would pay ![]() for each claim of i-type; however, because of the further excess of loss reinsurance, he pays:
for each claim of i-type; however, because of the further excess of loss reinsurance, he pays:
![]()
that is:
![]() (4)
(4)
We assume that all the premiums are paid using the expected value principle. Therefore, the reinsurance premium rate at time t is, for each class of risk:
![]()
where we have assumed the safety loading coefficients![]() , that is:
, that is:
![]() (5)
(5)
Therefore, after the reinsurances, the premium rate for the insurer is:
![]() (6)
(6)
3. The Problem
We assume that the insurer can choose, for every time![]() , the
, the ![]() and
and ![]() according to the observable information about the insurance risk processes up to time t. This means that
according to the observable information about the insurance risk processes up to time t. This means that ![]() and
and![]() , are the control parameters that allow us to consider the following set of admissible strategies:
, are the control parameters that allow us to consider the following set of admissible strategies:
![]()
The main goal for the insurer is to choose an optimal reinsurance strategy that maximize the expected exponential utility of terminal wealth. To solve this problem, we will use a dynamic programming approach.
After the reinsurance, remembering (4), referring to the j-th claim of type i, the insurer pays ![]()
![]()
Hence, the total claim amount charged to the insurer at time t, referred to the i-type claim is:
![]()
It follows that the surplus process ![]() controlled by the reinsurance strategies, evolves over the time as follows:
controlled by the reinsurance strategies, evolves over the time as follows:
![]() (7)
(7)
We recall that the process ![]() has a bivariate Poisson distribution with stationary increments; therefore, using results in [3] and [5] , it results that:
has a bivariate Poisson distribution with stationary increments; therefore, using results in [3] and [5] , it results that:
![]() (8)
(8)
We assume an insurer’s utility function ![]() with
with ![]() and
and![]() . In particular, let ube defined as follows:
. In particular, let ube defined as follows:
![]() (9)
(9)
The insurer looks for an optimal control strategy so as to maximize the expected utility of the terminal surplus under the initial condition regarding the x state at time t. We consider the following value function:
![]() (10)
(10)
with the boundary condition
![]() (11)
(11)
4. The Infinitesimal Generator and the HJB Equation
We are able to find the infinitesimal generator for the process ![]() and for the function This allows us to write the HJB equation; we prove the following theorem:
and for the function This allows us to write the HJB equation; we prove the following theorem:
Theorem 1. Let V be defined by (10) and let ![]() Therefore, V satisfies the following HJB equation:
Therefore, V satisfies the following HJB equation:
![]() (12)
(12)
Proof. We derive the following infinitesimal generator ![]() for the process
for the process ![]() and for the function V. The procedure is similar to that used in [7] and [8] .
and for the function V. The procedure is similar to that used in [7] and [8] .
![]()
Remembering (7) and (8), it results:
![]()
where we have:
![]()
![]()
![]()
and therefore we find:
![]()
the Equation (12) is therefore fulfilled by V.■
As we specified before, we assume the utility function (9), inspired by [1] [4] [8] - [10] , we look for a solution of the problem (10), with the condition (11) of the form:
![]()
with ![]()
We note that:
![]()
![]()
![]()
Therefore, (12) can be written as follows:
![]() (13)
(13)
Observing that:
![]()
it follows that Equation (13), dividing by ![]() and remembering (6), can be written as follows:
and remembering (6), can be written as follows:
![]() (14)
(14)
In the particular case where ![]() we obtain the case study regarding the only proportional reinsurance, as analyzed in [4] [8] ; under this assumption, Equation (6), remembering (3) and the assumptions made about the random variables
we obtain the case study regarding the only proportional reinsurance, as analyzed in [4] [8] ; under this assumption, Equation (6), remembering (3) and the assumptions made about the random variables![]() , gives:
, gives:
![]()
Therefore, (13) becomes:
![]() (15)
(15)
It is obviously that Equation (15) is the same equation found in [8] ; furthermore Equation (15) divided by ![]() coincides with Equation (3.4) of [1] with
coincides with Equation (3.4) of [1] with ![]() and
and ![]() calculated by means of the expected value principle.
calculated by means of the expected value principle.
In the particular case where![]() , we have the only excess of loss reinsurance case. Under this assumption, Equation (13), written on the form (14), is:
, we have the only excess of loss reinsurance case. Under this assumption, Equation (13), written on the form (14), is:
![]() (16)
(16)
In the following section we consider this case.
5. The Excess of Loss Reinsurance Case
We face the problem (16), with condition (11), that is ![]() We write (16) as follows
We write (16) as follows
![]() (17)
(17)
with conditions:
![]() (18)
(18)
and
![]() (19)
(19)
We have:
![]() (20)
(20)
and
![]() (21)
(21)
from which we deduce that, at the points where the gradient of g is zero, the Hessian matrix of ![]() is negative defined. The relative proof can be immediately obtained using results in [3] . We can therefore search the solution of the problem (17), with conditions (18), looking for the solutions of the following system:
is negative defined. The relative proof can be immediately obtained using results in [3] . We can therefore search the solution of the problem (17), with conditions (18), looking for the solutions of the following system:
![]()
that is, letting![]() , and remembering (20) and (21), we look for the solution of the system:
, and remembering (20) and (21), we look for the solution of the system:
![]() (22)
(22)
The solutions can be of the following four kinds:
![]()
We observe that the solution ![]() does not exist. Indeed, the system (22) gives:
does not exist. Indeed, the system (22) gives:
![]()
that is impossible.
According to results in [3] , we have:
![]() The system (22) can be written as:
The system (22) can be written as:
![]()
from which, if:
![]() (23)
(23)
we have:
![]()
![]() In a similar way to (II), if:
In a similar way to (II), if:
![]() (24)
(24)
we have:
![]()
![]() The system (22) gives:
The system (22) gives:
![]() (25)
(25)
In [3] , it is proved that under the assumption that both (23) and (24) are not satisfied, that is
![]() (26)
(26)
and
![]() (27)
(27)
the optimal strategy![]() , fulfilling (25), exists with
, fulfilling (25), exists with
![]() (28)
(28)
We observe that, from (28), being true also (27) and since ![]() fulfilled the system (25), it results that:
fulfilled the system (25), it results that:
![]() (29)
(29)
Finally, we recall that (23) and (24) are incompatible (see [3] ).
We are so able to find the value function, substituting the optimal strategy in (17), that is in (16), and obtaining ![]() with the condition
with the condition![]() . If (23) is fulfilled, we have:
. If (23) is fulfilled, we have:
![]() (30)
(30)
if (24) is fulfilled, it results:
![]() (31)
(31)
if (26) and (27) are at the same time fulfilled, we have:
![]() (32)
(32)
The results obtained in this section are collected within the following theorem.
Theorem 2. The optimal strategy ![]() concerning a whole excess of loss reinsurance and the corresponding value function are the following:
concerning a whole excess of loss reinsurance and the corresponding value function are the following:
・ if
![]()
it is
![]()
and
![]()
where ![]() is given by (30);
is given by (30);
・ if
![]()
it is
![]()
and
![]()
where ![]() is given by (31);
is given by (31);
・ if
![]()
and
![]()
it is
![]()
and
![]()
where ![]() is given by (32).■
is given by (32).■
Acknowledgements
We thank the Editor and the Referees for their comments.