Received 14 January 2016; accepted 7 March 2016; published 10 March 2016

1. Introduction
Geometry is a branch of mathematics that concerns itself with questions of shape, size, relative position of figures and properties of space. The foundation of Euclidean geometry is a group of elementary notions and axioms. In Euclidean geometry, which has been posed in modern terms by David Hilbert [1] , the elementary notions are the point, straight line and plane. His 20 axioms logically connect the elementary notions. In fractal geometry the elementary notions and axioms are not introduced. Instead, some basic notions are posed, the most important being the fractal set. These basic notions can be defined by means of mathematics. Using the Hausdorff (or capacity) dimensionformula, for every fractal set a fractal dimension can be calculated. We show that this value for the fractal dimension can be obtained using log-log method on a specific manner. The same method can be used for calculating the fractal dimension of nonfractal sets and natural objects as a problem of fractal analysis. Euclidian geometry relates to the artificial realities of the first, second and third dimensions. Fractal geometry is a branch of mathematics concerned with irregular patterns made of parts that are in some way similar to the whole. Unlike conventional geometry which is concerned with regular shapes and whole-number dimensions, fractal geometry deals with shapes that have non-integer or fractal dimensions. This geometry has proven to be a useful tool in analyzing various phenomena [2] since its meaning received a great deal of attention in many natural sciences and engineering. Now it has become widespread and multidisciplinary, and its applications have evolved into many disciplines. Compared to Euclidean geometry, which has a long history for more than 2000 years, fractal geometry is very new. Mandelbrot’s famous book “The Fractal Geometry of Nature” was published relatively recently, in 1982. Although conventional approaches based on Euclidean geometry can be well applied to describe regular geometries, it fails to describe the complex geometries. Fractal analysis consists of several methods (most of them being computer-based) useful to assign a fractal dimension and other fractal characteristics to a dataset in all areas of science. Although fractal geometry has been widely applied and used for quantitative morphometric studies of objects, mainly using fractal analysis and calculating the fractal dimensions of sets of objects [3] , there are still some unresolved issues that need to be addressed. Since some concepts of fractal geometry and fractal analysis are determined descriptively and/or qualitatively, this paper offers for some of them the more exact mathematical determination or explanation. Fractal geometry developed as a new geometry of nature [4] -[8] has been conceived with the aim to describe and evaluate the complexity and irregularity of shapes and processes in nature [3] . Up to now fractal geometry and fractal analysis are used in diverse research areas [9] -[12] . The goal of fractal geometry is to provide a platform for the demonstration of the importance of the fractal disciplines and to continuously explore the world of fractals not only in mathematics but also in sciences and technologies. One of the aims of the present paper is to show how fractal geometry gives rise to the fractal analysis confining our consideration to fractal sets and mathematics.
2. Methods and Results
2.1. The Geometrical Fractal Set
In Fractal geometry the geometrical fractal set should be considered as an infinite ordered series of geometrical objects defined on a metric space. To determine a fractal set we need specify three things [2] [13] [14] : 1) the shape of a starting object; (the initiator), 2) the iterate algorithm enabling its iterative application on the initiator and then, repeatedly, on all obtained geometrical objects (the generators), and 3) the conditions which these generators should satisfy, before all the properties of geometrical similarity (see Subsection 2.3). In that case, such geometrical object (generator) is called a prefractal [2] [4] [6] . The final result of such infinite procedure is the limit fractal or simply fractal [5] [8] . The initiator, prefractals and fractal represent the geometrical fractal set [13] [15] .
2.2. Koch Fractal Set
Basic definitions and laws of fractal planimetry can be demonstrated on some classical fractal models [3] [13] such as Cantor dust, Sierpinski gasket, Koch triadic curves, Mandelbrot set, etc. For that purpose we chose the triadic (snowflake) Koch curve set. The sequential construction of the this set can begin with the initiator which is an equilateral triangle of the edges length r0 (Figure 1(a)). The iterate algorithm to generate the set of Koch curves (prefractals) consists of recursive reduction of the straight line segments (or the scales) by 1/3 exchanging repeatedly the middle third of each side of the initiator, or a preceding generator, with two sides of a smaller,
![]() (a) (b) (c)
(a) (b) (c)
Figure 1. Koch fractal set. (a) Initiator-equilateral triangle, r0 is its side length; (b) The first stage of construction (z = 1), detail beyond the drawing is the corresponding generating element; (c) The second stage of construction (z = 2), detail beyond the drawing is the corresponding generating element.
equilateral triangle whose side is one-third the length of the previous side. The result after the first iteration (the stage of construction z = 1) is shown in Figure 1(b), and that after the second iteration (the stage of construction z = 2), in Figure 1(c). For the Koch prefractals, the length of a segment at the zth stage of construction (rz) and the number of segments at the same stage (Nz) are respectively,
 (1)
(1)
2.3. Geometrical Similarity
Similarity is a typical property of fractal sets. To define this concept we introduce a generating element of a generator. A generator is usually made up of straight-line segments (for example, see Figure 1). A logical concatenation of some segments of a generator can be thought of as the generating element [13] of a generator if the whole object can be completely built with such elements by their translations and/or rotations. For example, the drawing in Figure 1(b) can be subdivided into 3 generating elements, that in Figure 1(c) into 12 generating elements, and so on. In our example shown in Figure 1 the generators of the Koch prefractals, at the first and second stages of construction, have the generating elements made of four equal segments each, as shown as details below the drawings in Figure 1(b) and Figure 1(c). Two successive generating elements of two generators of a set of objects can be geometrically similar or not. According to the definition of similarity in Euclidean planimetry, two generating elements of the generators at stages z and z + 1 (say, those in Figure 1(b) and Figure 1(c)) are similar to each other [16] if (1) the ratio of the measure of a segment of the generating element at stage z + 1 and the measure of the corresponding segment of the element at the stage z is constant for all pairs of corresponding segments (e.g., for the four pairs of segments of the two mentioned details in Figure 1) and for all z, and (2) the angles between the pairs of corresponding segments of the two generating elements are congruent.
2.4. The Capacity Dimension
Fractal dimension is a quantitative measure of morphological complexity of an object. There are many different definitions of fractal dimension [2] . Mandelbrot [8] thinks that the “plethora” of distinct definitions of the fractal dimension should be reduced to two: the similarity dimension and Hausdorff dimension. The similarity dimension is basic dimension related to all similar (fractal) sets but this dimension is not the subject of our study. The most important definitions are the Hausdorff and capacity dimensions [2] . These two dimensions are quite similar [2] , but the Hausdorff dimension is rather sophisticated, being a subject of mathematical measure theory. The capacity dimension can be given by [2]
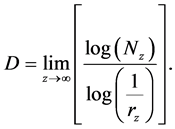 (2)
(2)
Since the logarithm is defined only for dimensionless values (numbers), not for physical quantities like 1/r (where r is a length), we define the modified capacity dimension as:
 (3)
(3)
where r0 is a reference scale [17] [18] (for example, r0 can be the length r0 of the scale of an initiator of the Koch set, Figure 1). The quantity r0 (Equation (1)) could be included into the definition of the capacity dimension (Equation (3)) because the ratio r0/rz in Equation (3) is a dimensionless quantity (a number).
If we submit Equation (1) into the last definition (Equation (3)) and put z to tend to infinity, one can see that the expression in Equation (3) gives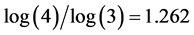 :
:
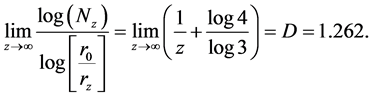 (4)
(4)
Fractal dimension D is the main quantifier to measure complexity of a set of geometrical and natural objects. The larger the D, the higher the complexity of the set is. For example, since the fractal dimension of the Sierpinski set is , it means that the last set is more complex than the Koch set (Equation (4)).
, it means that the last set is more complex than the Koch set (Equation (4)).
2.5. Log-Log Method
Considering Equation (3) it would be interesting to analyze a relation between Nz and rz of the Koch fractal set in a log-log coordinate system. If along the horizontal coordinate axis we put the values rz = 1/3z for  (the value of r0 is set to 1for visual clarity) and along the vertical coordinate axis the values of
(the value of r0 is set to 1for visual clarity) and along the vertical coordinate axis the values of  also for
also for  and fit the power function to these data using Microsoft Excel software, the decreasing straight line graph shown in Figure 2 is obtained. The fitting power function is:
and fit the power function to these data using Microsoft Excel software, the decreasing straight line graph shown in Figure 2 is obtained. The fitting power function is:
![]()
Figure 2. Log-log method applied to the Koch construction (the beginning of the construction is shown in Figure 1). The fitting graph of relationship between the number of segments and segment sizes (in cm) is a decreasing straight line with the high coefficient of determination R2.
 (5)
(5)
with the coefficient of determination R2 = 1. The fitting parameter is −1.262 which is equal to the negative fractal dimension of the Koch fractal set already obtained using the formula for modified capacity dimension (Equation (3)). This procedure can be thought of as the log-log method. This method is also used in many other fractal techniques, particularly in computer-based ones.
2.6. A Nonfractal Set
Following the fractal methodology, we inscribe an equilateral triangle (as the initiator) in a circle of unit radius (Figure 3(a)) and state the following iterate algorithm: from the middle of each triangle side the normal is erected to the sections with the circle. These three sections are connected to the nearest vertices of the triangle sides forming a hexagon inserted in the circle (Figure 3(b)). The result of the next iteration (Figure 3(c)) is a dodecagon. The next polygons can be constructed using the same algorithm. Inspecting the details below the drawings in Figure 3(b) and Figure 3(c), which are the generating elements for these polygons (generators), it is obvious that they are not mutually similar since the angles between the corresponding segments of the generating elements are different. The condition of side ratios constancy (geometrical similarity) also fails. Namely, it is known that for a circle of unit radius:
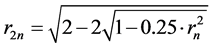 (6)
(6)
where rn is the side length of a regular polygon inserted in the circle, n is the number of sides of the polygon and r2n is the side length of the polygon with 2n sides. From this expression it is obvious that the ratio r2n/rn is not constant for every n (e.g., r6/r3 = 0.577, r12/r6 = 0.518 etc.), so that the class of such regular polygons inscribed in a circle cannot be considered as a set of prefractals. If n tends to infinity, the polygons tend to the circle, which is not a limit fractal. Therefore this set of regular polygons inscribed in a circle cannot be a fractal set.
On the other hand, if we apply the log-log method to the data of the polygonal set obtained, a straight-line graph is again obtained (Figure 4). The equation of this graph is
 (7)
(7)
which is analogous to Equation (6). From this equation the fitting parameter −1.027 corresponds to the negative value of the fractal dimension D of the nonfractal set considered. This is the fractal dimension of a circle of unit radius (which is the limit object). Using the mass method Smith et al. [3] have measured the fractal dimension of a circle and found D = 1.02. Using mathematics (with no measurements) we found for a circle of unit radius a more precise value D = 1.027 (Equation (7)).
2.7. Properties of Fractal and Nonfractal Sets
The main properties of geometrical fractal sets are geometrical self-similarity and scale invariance. The object’s
![]() (a) (b) (c)
(a) (b) (c)
Figure 3. Nonfractal set of regular polygons. (a) Initiator- equilateral triangle inscribed in a circle of unit radius; (b) The first stage of construction (z = 1) is a hexagon; the detail beyond the drawing is its generating element; (c) The second stage of construction (z = 2) is a dodecagon with the corresponding generating element.
![]()
Figure 4. Log-log method applied to the set of polygons (Figure 3). The fitting graph is a decreasing straight line (see Figure 2 for comparison).
property known as self-similarity was first coined by Mandelbrot [5] . It can be geometrical or statistical. A fractal pattern is said to be geometrically self-similar if every small piece of an object resembles the whole object. This definition of the concept “geometrical self-similarity” should be quantified since small pieces that constitute geometrical or natural objects are rarely copies of the whole object [14] . We have offered a more exact interpretation of this descriptive definition introducing a generating element of a generator as a “small piece”. Therefore every fractal set (which must satisfy geometrical similarity) should satisfy the property of geometrical self-similarity since by definition every small generating element is always similar to any other large generating element.
Scale invariance is a feature of objects or laws that they do not change if scales of length or other variables are multiplied by a common factor. For example, this common factor for the Koch fractal set is 1/3. If r0 is 1 cm (Figure 1(a)), the length of the segment in Figure 1(b) is 1/3 cm, that in Figure 1(c) is 1/9 cm, etc. This means that if we multiply the length of each segment of the generating element in Figure 1(b) by 1/3, the same but reduced generating element of the prefractal shown in Figure 1(c) will be obtained. Nonfractal sets cannot satisfy geometrical similarity and properties of fractal sets.
2.8. A Fractal Set versus a Nonfractal Set
We showed that Koch set is a fractal set because it satisfies the geometrical similarity. It means that the ratio rz+1/rz is the same for every z. If z tends to infinity, we obtained the limit fractal which cannot be drawn or imagined. Nevertheless this fractal exists because we calculated the fractal dimensions of the limit fractal using both the formula for modified capacity dimension (Equation (3)) and log-log method. In both cases we found a real and finite value D = 1.262. We conducted the same procedure using the set of polygons inscribed in a circle. Although the polygonal set is not a fractal set we calculated the fractal dimension of this limit object using the log-log method. In fact, we calculated the fractal dimension of the circle which corresponds to the limit object in which the set of polygons is inscribed. Besides, the initiator in Fractal geometry is included into the fractal iterations as a part of prefractals while the starting object (the circle) in fractal analysis does not change its integrity during iterations.
The circle is a closed line, but the log-log method can be applied to any open line (Figure 5). We found that in Fractal geometry the values of segment lengths were strongly determined by the property of geometrical similarity, while in the fractal analysis values and shapes of open lines are not restricted (Figure 5 and Figure 6). Fractal analysis represents a formation of Fractal geometry consisting in using log-log and others methods [3] , and ignoring the property of geometrical similarity. Therefore we can use any set of regular polygons and always calculate the fractal dimension of the object in which these polygons are inscribed. For example, fractal analysis enables to calculate the fractal dimension of the border of any natural object (not of the set of objects) inscribing a set of straight lines of known and constant lengths along the object’s border and count the number of segments. These data in a log-log coordinate system give the fractal dimension of the natural object (coastlines, borders between nations, dendrites of neurons etc.). This method has been the basis of the Richardson’s method of fractal dimension measurement of natural objects [19] . It may be opportune to underline that an unlimited extension of log-log coordinate system is not valid when natural and biological objects are investigated. As previously reported, the fractal dimension could be reliable evaluated within a defined scale interval, called “fractal window” [17] [18] .
![]()
Figure 5. The fractal dimension of an open circle-like curved line. (a) The circle-like line considered, the length of a straight line segment is 1.5 cm, the bar is 1 cm; (b) Relation between N and r represented in a log-log coordinate system, the graph is a straight line whose exponent represents a negative value of the fractal dimension of the curve, R3 is the coefficient of determination.
![]()
Figure 6. The fractal dimension of an open wavy line. (a) The curved line considered, the length of a straight line segment is 2.2 cm, the bar is 1 cm; (b) Relation between N and r, the graph is a result of application of the log-log method and re- presents a decreasing straight line whose exponent is a negative value of the fractal dimension of the curve in (a).
2.9. Richardson’s Method
The polygonal method needs a group of about ten printed copies of a considered line and in each of them inscribes different regular polygon (Figure 5 and Figure 6). This method is rather tedious and time-consuming. A simpler but still time-consuming method is presented in Richardson’s paper [20] . Richardson, as a physicist and Quaker, wondered if there are more wars between nations that share longer common border. Answering this question required measurement of the national borders lengths. To measure the length of the border drawn on a map of Atlas, he used as a ruler a divider having sharp points at the ends of both arms. For a given distance between the sharp points of the divider the total length of the border was given by the number of divider’s steps along the border multiplied by the divider step size.
Since the length of a polygon’s segment (Figure 5 and Figure 6) is the same as the corresponding divider’s step size, all the measurements can be done on one printed line. We used this method when preparing Figure 2(b), Figure 4(b), Figure 5 and Figure 6.
The term fractal was introduced by Mandelbrot based on his paper on self-similarity [21] . In that paper, Mandelbrot cited previous work by Richardson [20] and noted that the diagrams presented in Richardson’s paper lead to the conclusion that approximate length of the border between two nations can be given by the relationship [8]
![]() (8)
(8)
where the value of the exponent D seems to depend upon the shape of the border chosen. Topology fails to discriminate between different borders [8] . Since Equation (9) can be rewritten as
![]() (9)
(9)
it is obvious that the factor Fr−D corresponds to the number of divider’s steps. For a given r the border of smaller length has smaller number of steps (smaller F) in relation to a longer border of the same shape (the same D) which has larger number of steps (larger F).
To Richardson, the D was a fitting parameter of no particular significance. Having in mind “unearthed” Richardson’s work in which he claimed that his lines’ slopes had no theoretical interpretation [8] , Mandelbrot claimed that the exponent D should be interpreted as a fractal dimension. We find that among many fractal analysis techniques, only Richardson’s method enables correct calculation of the length of an object’s border or irregular line.
3. Discussion
When the physical or biological problem is stated in mathematical terms, dimensional balance should be a routine part of the solution of any problem. Exponents and logarithms must always be dimensionless [22] . When dimensioned quantities appear in exponents or in logarithms, they must be combined with the same dimensioned quantities so that their quotient or product is dimensionless [17] [18] . It seems that some of the authors do not take care of these facts. The problem is particularly distinct in defining the fractal dimensions in fractal geometry [2] [13] [23] [24] . One of the main aims of the present study is to define and discuss physically correct of modified capacity dimension. Bassingthwaighte et al. [2] noted that the capacity dimension tells us how much balls needed to cover the object when the size of the balls (r) decreases. In the analytical definition of capacity dimension there exists log (1/r). West and Deering [13] have defined the similarity dimension as the ratio of two logarithms log N/log (1/r). In defining the box-counting dimension Falconer [23] showed lower and upper box- counting dimension by the expression containing log δ where δ is the diameter of a corresponding set. Edger [24] also used log (1/r) in the definition of the upper box-counting dimension, where r is a diameter of the set. Richardson’s method of measuring the fractal dimension is robust with very high correlation coefficients but it is, at the same time, tedious and time-consuming. Therefore, the need for more handsome methods for that measurement emerges. The conventional and most popular box-counting (computer-based) method is one suitable to measure the fractal dimensions of geometrical and natural objects. This method is commonly used among other fractal techniques [3] -[5] . Unfortunately, it seems that this method demonstrates some mistakes. Using this method we showed that the fractal dimension of a straight line segment is 0.927 not 1. The fractal dimension of a circle of the radius 1 cm obtained using purely mathematical method, is 1.027, while that measured using the box-counting method is larger than 1.15. The fractal dimension increases with the resolution of a figure and depends on its position on the screen. We showed that Richardson’s method does not depend on these factors.
NOTES
![]()
*The present paper is dedicated to the imperishable memory of Professor Benoît Mandelbrot, who passed away October 10, 2010.
#Corresponding author.
†These two authors contributed equally.