Uncertain Volatility Derivative Model Based on the Polynomial Chaos ()
Received 5 November 2015; accepted 16 February 2016; published 19 February 2016

1. Introduction
Several works were presented in the past for uncertainty quantification of derivative pricing due to random volatility. In [1] a new model for pricing and hedging derivative securities and option portfolios in an environment where the volatility is unknown and assumed to be ranged between two extreme values σmin and σmax was presented. The bound of volatility is computed by historical high-low peak of stock or option-implied volatilities and works as confidence interval for future volatility values. The derivative asset which arises as the volatility paths varies in such a band can be described by a non-linear PDE, which we call the Black-Scholes-Barenblatt equation. In [2] the pricing of contingent claims in a multidimensional frictionless security market assumed that the volatility of the security process is a known function of price and time. The author’s approach was underpinned by the theory of totally non-linear parabolic partial differential equations and the non-stochastic approach to Itô’s formation. In [3] the volatility is considered as a random variable, which exhibits an adequate distribution like uniform type, Gaussian type or others. Thus the deterministic parabolic equation changes into a parabolic equation with stochastic input, where the solution represents a random field. Method of lines used for the numerical solution of the system resulting from the generalized polynomial chaos and corresponding end- boundary value problems of a parabolic equation was solved numerically in a Monte Carlo simulation. In [4] the effect of uncertainty in the volatility parameter σ on the Black-Scholes price of the European and American put was quantified. Probabilistic uncertainty analysis to the Black-Scholes model was carried out and the results are compared with those of the Uncertain Volatility model. The probability distribution for the volatility calibrated from historical data. The Monte Carlo (MC) and a surrogate Polynomial Chaos (PC)/MC methods were used to compute uncertainty bounds. The effect of the parametric uncertainty is investigated at the end.
In the current work a robust algorithm based on the stochastic finite element method using the generalized polynomial chaos was developed and it is considered as a general method for derivative pricing where the volatility input is considered as a random variable.
2. Finite Element Formulation of Black-Sholes Equation
Suppose 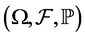 is a probability space with a filtration
is a probability space with a filtration . Where
. Where 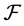 is the σ-algebra and is considered to contain all the information that is available,
is the σ-algebra and is considered to contain all the information that is available,  is the probability measure. Consider a market consists of two assets, a risk free bond of constant interest rate r and a stock with a price process
is the probability measure. Consider a market consists of two assets, a risk free bond of constant interest rate r and a stock with a price process 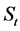 evolving according to a geometric Brownian. The dynamic of assets are given by:
evolving according to a geometric Brownian. The dynamic of assets are given by:
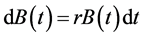 (1)
(1)
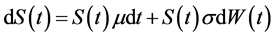 (2)
(2)
where the drift rate μ and the volatility σ > 0 are assumed to be constant, and W(t) is a standard Brownian motion. The aim is to price a derivative of the form  under uncertain volatility. In the basic theory of Black- Sholes the volatility of risky asset assumed to be constant which is results in mispricing of contingent claims due to uncertainty on the choice of the values within this model. As discussed in the previous paragraph in the current work the volatility considered as a stochastic process
under uncertain volatility. In the basic theory of Black- Sholes the volatility of risky asset assumed to be constant which is results in mispricing of contingent claims due to uncertainty on the choice of the values within this model. As discussed in the previous paragraph in the current work the volatility considered as a stochastic process  following the uncertainty of the market prices. The distribution of volatility assumed to be lognormal and if the price of the derivative has the form
following the uncertainty of the market prices. The distribution of volatility assumed to be lognormal and if the price of the derivative has the form 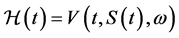 which is constintent with the absence of arbitrage then the function
which is constintent with the absence of arbitrage then the function 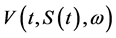 is the solution of the following boundary value problem:
is the solution of the following boundary value problem:
 (3)
(3)
In essence the solution of the problem is a function of the form  for every fixed t, i.e. a stochastic process and is not a deterministic function.
for every fixed t, i.e. a stochastic process and is not a deterministic function.
To solve the problem, we switch to the log-price process 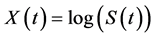 which is the solution of the equation:
which is the solution of the equation:
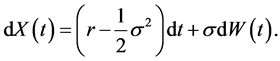 (4)
(4)
The infinitesimal generator for this process has constant coefficients:
![]() (5)
(5)
Thus by setting ![]() the Equation (3) becomes:
the Equation (3) becomes:
![]() (6)
(6)
In order to solve the problem according to the finite element method in the current paper we consider a linear
element with nodes![]() . To each node
. To each node ![]() there is a hat function
there is a hat function![]() . To solve the problem as-
. To solve the problem as-
suming a test v function belongs to the space:
![]() (7)
(7)
Using a test function v and integrating by parts over the domain D the variational formulation of the Black- Scholes equation has the following form:
![]() (8)
(8)
Using the matrix notation the equation takes the following form:
![]() (9)
(9)
where:
![]() (10)
(10)
3. Stochastic Galerkin Solution
The author has presented a stochastic finite element procedure to solve boundary problems using polynomial chaos [5] -[9] . The outcome derivative price of the problem is given by the polynomial chaos expansion as:
![]() (11)
(11)
where the order Q and the formula ψ of Polynomial Chaos are given in Appendix.
According that and using the inner product of the equation on each polynomial of the ![]() base we get:
base we get:
![]() (12)
(12)
Making the replacement of matrices and assuming ![]() the density function we take the equation:
the density function we take the equation:
![]() (13)
(13)
This is equivalent with:
![]() (14)
(14)
To simplify the form make the following:
![]() (15)
(15)
4. Time Discretization
According to the previous replacement we discretize the Equation (14) using the theta-scheme with constant time step Δt. The finite element mesh considered as uniform and the Equation (14) takes the following form:
![]() (15)
(15)
Equivalent
![]() (16)
(16)
The statistical moments of the outcome derivative price arise by the properties of the Polynomial of Chaos expansion:
The expected value:
![]() (17)
(17)
and the variance:
![]() (18)
(18)
5. Numerical Example
For the numerical example of derivative pricing a plain vanilla European Put Option was chosen. The historical data of S&P 500 was used to compute the mean value and the volatility of the index volatility. Based on the mean and max value of volatility and its mean volatility of volatility the option price has been calculated with expiration time T = 90/360 and strike price K = 1200. The statistical value of historical data for volatility for a period from 2000-2014 are given in Table 1. In Figure 1 and Figure 2 the Daily Return and the volatility of S&P 500 are presented.
To verify the model we compare the results with those raised by the Monte Carlo method which is treated as the exact solution. The computational implementation of the Monte Carlo Method leads to the random process
generation of ![]() and the requested
and the requested ![]() gets a new value
gets a new value ![]() for each realization, where
for each realization, where
![]() . At the end of all simulations the statistical moment are calculated.
. At the end of all simulations the statistical moment are calculated.
The expected value and the variance are given by:
![]()
![]()
Figure 1. Daily returns of S&P 500 for the period 2000-2014 (Yahoo finance).
![]()
Figure 2. 30 day volatility of S&P 500 for the period 2000-2014 (Yahoo finance).
![]()
Table 1. Statistical values of volatility of S&P 500 for the period 2000-2014.
Two different cases were carried out (Table 2).
In the Figure 3 and Figure 4 the results of the statistical moments of the derivative pricing are presented and high accuracy is realized. The effect of volatility uncertainty on the statistical moments of option price presented in Figure 5 and Figure 6. For 10 values of index volatility of volatility with a mean value equal to 40% and input parameters as before, 10 different calculations were carried out and the results are presented. The increase of vol of vol causes a decrease in expected option price of 12% approximately at the maxim while results a huge increment on its volatility as presented in Figure 6.
6. Conclusion
A new algorithm of volatility uncertainty propagation in the derivative pricing and hedging procedure was presented according to the Black-Sholes PDE. A stochastic finite element method using generalized polynomial chaos was used to develop an algorithm of uncertainty propagation solving finally a deterministic problem for the derivative pricing. The results of Monte Carlo Method for the derivative’s distribution were used as the exact solution against those rose from the new algorithm. The method leads to high accuracy and eliminates the large number of the Monte Carlo Method’s simulations. The model applied using the historical data of S&P 500 for
![]()
Figure 5. Expected option price ATM via stock volatility of volatility.
![]()
Figure 6. Volatility of option price ATM via stock volatility of volatility.
the period 2000-2014. The mean value and the volatility of volatility of index are used for the pricing of a plain vanilla European put option considering the volatility parameter as a stochastic process. The effect of index volatility of volatility on the derivative price distribution was analyzed and the results were presented by the two methods. High uncertainty of index volatility leads to a highly non linear increase of option price volatility as the results of analysis are shown.
Appendix
Galerkin Approximation and Generalized Polynomial of Chaos
In order to solve the problem 3 we have to create the new space![]() . For that reason the subspace
. For that reason the subspace ![]() is considered as [10] .
is considered as [10] .
![]() (A.1)
(A.1)
Using the dyadic product of the space ![]() the space
the space ![]() created. Thus
created. Thus
![]() (A.2)
(A.2)
The space ![]() has dimension QN and regards the test function v. In the case where exists
has dimension QN and regards the test function v. In the case where exists ![]() finite element supported by boundaries condition then the subspace of solution belongs is:
finite element supported by boundaries condition then the subspace of solution belongs is:
![]() (A.3)
(A.3)
Assuming that the ![]() represents a space of univariate orthonormal polynomial of variable
represents a space of univariate orthonormal polynomial of variable ![]() with order k or lower and:
with order k or lower and:
![]() (A.4)
(A.4)
The tensor product of the M ![]() subspace results the space of the Generalized Polynomial Chaos:
subspace results the space of the Generalized Polynomial Chaos:
![]() (A.5)
(A.5)
And using (A4)
![]() (A.6)
(A.6)
where![]() .
.
And
![]() . (A.7)
. (A.7)
Xiu & Karniadakis [11] show the application of the method for different kind of orthonormal polynomials and in the current paper the Hermite polynomial was used with the following characteristics:
![]()
![]() (A.8)
(A.8)
where:
![]() : are the normalization factors,
: are the normalization factors, ![]() is the Kronecker delta.
is the Kronecker delta.
![]() : is the density function and
: is the density function and
![]() . (A.9)
. (A.9)
For a 3rd order of one dimension of uncertainty the Hermite Polynomial Chaos is given by:
![]() ,
, ![]() ,
,![]() .
.