A Renormalizable Theory of Quantum Gravity: Renormalization Proof of the Gauge Theory of Volume Preserving Diffeomorphisms ()
Keywords
Renormalization Proof of Gauge Field Theory of Volume-Preserving Diffeomorphisms

1. Introduction
As of today a viable quantum field theory of gravitation has proven to be elusive [1] [2] .
At the microscopic level the Standard Model (SM) of particle physics successfully describes the electromagnetic, weak and strong interactions based on quantized gauge field theories with the finite-dimensional compact gauge groups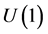 ,
, 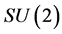 and
and 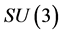 respectively [3] -[8] .
respectively [3] -[8] .
At the macroscopic level General Relativity (GR) successfully describes the gravitational interaction based on a classical gauge field theory with the non-compact diffeomorphism group of four-dimensional spacetime 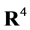 as the gauge group [9] -[11] .
as the gauge group [9] -[11] .
When trying to naively generalize the successful aspects of the gauge field theory ansatz to describe gravity at the quantum level one encounters unsurmountable difficulties—quantizing GR leads to a non-renormalizable theory and working with other finite-dimensional compact gauge groups to generalize that the SM yields no description of gravity.
Whatever one tries one seems to bang one’s head against two unremovable, yet intertwined roadblocks: 1) against GR and—underpinning it—the Principle of Equivalence stating that inertial and gravitational masses are equal which forces a geometric description of gravity, and 2) against the seeming non-viability of gauge theories with non-compact gauge groups.
In this and a series of related papers [12] -[14] , we have systematically analyzed both roadblocks and 1) asked ourselves what physics at the quantum level we get when discarding the equality of inertial and gravitational mass for virtual quantum states and 2) made technical progress in formulating renormalizable gauge field theories based on a non-compact gauge group.
Before turning to the technical renormalization analysis, let us illuminate both aspects a bit more in detail.
1.1. Physical Aspect: Why Should Inertial and Gravitational Mass Be the Same for Virtual Quantum States?
GR has been developed starting from the observed equality of inertial and gravitational mass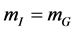 . To be in agreement with observation, this equality has to hold in any expression describing observable states in a gravitational context in their rest frames. However, in formulating a theory, nothing enforces this equality for virtual (=non-observable) quantum states as long as it continues to hold for the on-shell (=observable) quantum states in that theory.
. To be in agreement with observation, this equality has to hold in any expression describing observable states in a gravitational context in their rest frames. However, in formulating a theory, nothing enforces this equality for virtual (=non-observable) quantum states as long as it continues to hold for the on-shell (=observable) quantum states in that theory.
Now (a) the observed equality of inertial and gravitational mass of an on-shell physical object in its rest frame together with (b) the conservation of the inertial energy-momentum  in any frame tells us that in the rest frame
in any frame tells us that in the rest frame
 (1)
(1)
assuming that the gravitational energy-momentum  plays a physical role different from that of the inertial energy-momentum, yet being observationally identical for on-shell objects. However, for off-shell states why shouldn’t there be two separate conservation laws, one for the inertial energy-momentum and the other for the gravitational energy-momentum?
plays a physical role different from that of the inertial energy-momentum, yet being observationally identical for on-shell objects. However, for off-shell states why shouldn’t there be two separate conservation laws, one for the inertial energy-momentum and the other for the gravitational energy-momentum?
To explore this route, let us postulate both 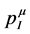 and
and  to be two separate four-vectors which are conserved, but in our approach through two different mechanisms. The conservation of
to be two separate four-vectors which are conserved, but in our approach through two different mechanisms. The conservation of 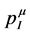 is related to translation invariance in spacetime. Making use of Noether’s theorem a second conserved four-vector can be constructed which is related to the invariance under volume-preserving diffeomorphisms of a four-dimensional inner space. That four-vector is then interpreted as the gravitational energy-momentum
is related to translation invariance in spacetime. Making use of Noether’s theorem a second conserved four-vector can be constructed which is related to the invariance under volume-preserving diffeomorphisms of a four-dimensional inner space. That four-vector is then interpreted as the gravitational energy-momentum  in the construction of a gauge theory of gravitation [14] .
in the construction of a gauge theory of gravitation [14] .
The observed equality of inertial and gravitational energy-momentum in this approach is assured by taking a gravitational limit for on-shell observable physical objects equating gravitational and inertial energy-momentum, the construction of which is based on the analysis of asymptotic states and the definition of a suitable 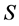 -matrix in the theory [14] .
-matrix in the theory [14] .
1.2. Technical Aspect: Why Should Viable Quantum Gauge Field Theories Be Limited to Finite-Dimensional Compact Gauge Groups?
In the process of constructing the gauge theory of volume-preserving diffeomorphisms of a four-dimensional inner space which emerges from the above thinking, we have to deal with new difficulties arising from the noncompactness of the gauge group. 1) The gauge field Hamiltonian is not manifestly positive definite which is cured by a natural condition on the support of the gauge fields in inner space [12] . 2) The quantization and subsequent derivation of Feynman rules yield no additional complications in comparison to the Yang-Mills case w.r.t. spacetime-related expressions, but it yields badly divergent-looking integrals over inner momenta related to the infinite volume of the gauge group—a phenomenon which does not plague Yang-Mills theories due to the assumed gauge group compactness. 3) As already mentioned, a gravitational limit for on-shell observable physical objects has to be taken to ensure the observed equality of inertial and gravitational energy-momentum. This limit has to respect the unitarity of the physical S-matrix which we have established in [14] .
In [13] we have dealt with issues 1) and 2) at the one-loop level and established that the pure gauge field theory is asymptotically free whereas the inclusion of all SM fields destroys asymptotic freedom, hence assuring the observability of the gauge field quanta. To demonstrate the fundamental viability of the theory beyond one loop, however, we have to give both a proof of its renormalizability w.r.t. the occurring spacetime divergences as well as to propose a general approach dealing with the inner divergences, both of which we provide in this paper.
In the process we establish a well-defined perturbative expansion of the quantum effective action demonstrating its spacetime renormalizability and the existence of regularization schemes for the inner momentum integrals consistent with the symmetries of the theory. In fact, the spacetime-renormalized and inner-space-regularized quantum effective action defines a viable quantum field theory for each regularization scheme in terms of the original finite number of coupling constants, masses etc.
Stated otherwise it is possible to consistently establish a quantum gauge field theory not only for compact gauge groups, but also for at least the non-compact gauge group of volume-preserving diffeomorphisms. The price to pay comes in the form of an additional regularization scheme for the divergent sums over inner degrees of freedom—each such scheme which is compatible with the symmetries of the theory establishes one welldefined version of the quantum theory belonging to the classical gauge theory one starts with. And each such version with its finite number of coupling constants, masses etc. yields as precise predictions as do its YangMills cousins—predictions which are equal for all such versions at tree level, but depend on the chosen regularization scheme for the loop contributions. In exactly the same way as experiment has to tell the physical values of the various couplings, masses etc. in this or the Yang-Mills cases, experiment ultimately has then to choose the regularization preferred by Gravity.
So let us turn to implement the program outlined above.
2. Classical Gauge Theory of Volume-Preserving Diffeomorphisms
In this section we review the basics of the gauge theory of volume preserving diffeomorphisms as presented in [12] .
Let us start with a four-dimensional real vector space 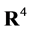 with elements labelled
with elements labelled 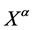 without a metric structure at this point which we will call inner space in the following. Volume-preserving diffeomorphisms
without a metric structure at this point which we will call inner space in the following. Volume-preserving diffeomorphisms
 (2)
(2)
act as a group 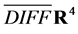 under composition on this space.
under composition on this space. 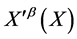 denotes an invertible and differentiable coordinate transformation of
denotes an invertible and differentiable coordinate transformation of 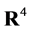 with unimodular Jacobian
with unimodular Jacobian
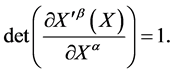 (3)
(3)
Next we want to represent this group on spaces of differentiable functions 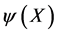 which will in differentialgeometrical terms later serve as fibres and sections respectively of the vector bundles to be constructed. To be specific we require the
which will in differentialgeometrical terms later serve as fibres and sections respectively of the vector bundles to be constructed. To be specific we require the 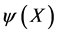 to be differentiable functions on the inner space introduced above and to be integrable such that the scalar product
to be differentiable functions on the inner space introduced above and to be integrable such that the scalar product
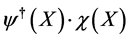
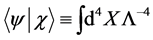 (4)
(4)
is well-defined. Above we have introduced a parameter 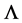 of dimension length,
of dimension length,  , so as to define a dimensionless scalar product.
, so as to define a dimensionless scalar product.
Turning to the passive representation of  in field space for infinitesimal transformations
in field space for infinitesimal transformations 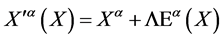 with
with 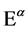 dimensionless we have
dimensionless we have
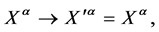 (5)
(5)
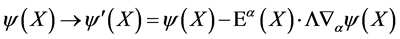
transforming the fields only, where  represents partial differentiation in inner space.
represents partial differentiation in inner space.
The unimodularity condition Equation (3) translates into the infinitesimal gauge parameter 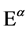 being divergence-free
being divergence-free
 (6)
(6)
Note the crucial fact that the algebra 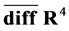 of the divergence-free
of the divergence-free 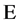 s closes under commutation. For
s closes under commutation. For 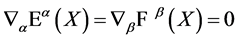 we have
we have
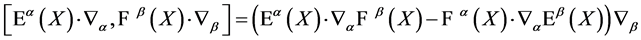 (7)
(7)
with
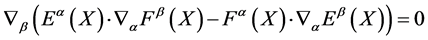 (8)
(8)
as required by the finite transformations  forming a group under composition.
forming a group under composition.
As a result we can write infinitesimal transformations in field space
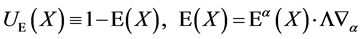 (9)
(9)
as anti-unitary operators w.r.t. the scalar product Equation (4). Both the 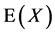 and the
and the 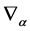 are anti-hermitean w.r.t. the scalar product Equation (4). The decomposability of
are anti-hermitean w.r.t. the scalar product Equation (4). The decomposability of 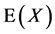 w.r.t. to the operators
w.r.t. to the operators 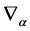 will be crucial for the further development of the theory, especially for identifying the gauge field variables of the theory.
will be crucial for the further development of the theory, especially for identifying the gauge field variables of the theory.
Introducing the variation 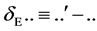 of an expression under a gauge transformation we can finally write
of an expression under a gauge transformation we can finally write
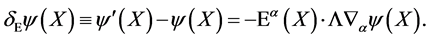 (10)
(10)
In mathematical terms we have just reviewed the group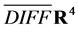 , the algebra
, the algebra  and defined their representations on a suitable space of functions. Note that spacetime has played no role so far.
and defined their representations on a suitable space of functions. Note that spacetime has played no role so far.
Next we turn to the four-dimensional Minkowski spacetime (M4,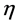 ) with metric
) with metric 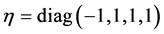 and elements labelled
and elements labelled 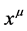 which will serve as the base space of the vector bundles we construct.
which will serve as the base space of the vector bundles we construct.
Extending the global volume-preserving diffeomorphism group to a group of local transformations we allow 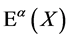 to vary with
to vary with  as well, i.e. we allow for
as well, i.e. we allow for 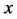 -dependent volume-preserving infinitesimal gauge parameters
-dependent volume-preserving infinitesimal gauge parameters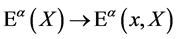 . To represent the group we have to allow the functions
. To represent the group we have to allow the functions 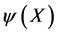 to become
to become 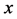 -dependent fields
-dependent fields 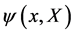 as well.
as well.
We note that these fields 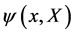 might live in non-trivial representation spaces of both the spacetime Lorentz group with spin
might live in non-trivial representation spaces of both the spacetime Lorentz group with spin  and of other symmetry groups such as
and of other symmetry groups such as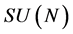 . These representations factorize w.r.t. the inner diffeomorphism group representations we introduce below which is consistent with the Coleman-Mandula theorem.
. These representations factorize w.r.t. the inner diffeomorphism group representations we introduce below which is consistent with the Coleman-Mandula theorem.
In generalization of Equation (9) we thus consider
 (11)
(11)
The formulae Equation (5) together with Equation (6) with the fields now  -dependent as well still define the representation of the volume-preserving diffeomorphism group in field space.
-dependent as well still define the representation of the volume-preserving diffeomorphism group in field space.
Next we introduce a covariant derivative  which is defined by the transformation requirement
which is defined by the transformation requirement
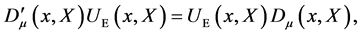 (12)
(12)
where  denotes the gauge-transformed covariant derivative.
denotes the gauge-transformed covariant derivative.
To fulfil Equation (12) we make the usual ansatz
 (13)
(13)
decomposing 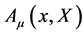 w.r.t. the generators
w.r.t. the generators 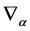 of the diffeomorphism algebra in field space. In order to have the gauge fields in the algebra
of the diffeomorphism algebra in field space. In order to have the gauge fields in the algebra 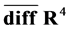 we impose in addition
we impose in addition
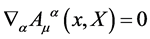 (14)
(14)
consistent with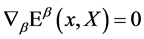 . As a consequence the usual ordering problem for
. As a consequence the usual ordering problem for 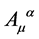 and
and 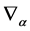 in the definition of
in the definition of 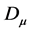 does not arise and
does not arise and  is anti-hermitean w.r.t. to the scalar product
is anti-hermitean w.r.t. to the scalar product
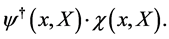
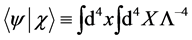 (15)
(15)
The requirement Equation (12) translates into the transformation law for the gauge field
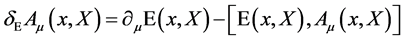 (16)
(16)
which reads in components
 (17)
(17)
respecting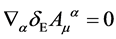 .
.
Note that the consistent decomposition of both 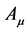 and
and 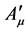 w.r.t. the generators
w.r.t. the generators 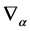 is crucial for the theory’s viability. It is ensured by the closure of the algebra Equation (7) and the gauge invariance of
is crucial for the theory’s viability. It is ensured by the closure of the algebra Equation (7) and the gauge invariance of 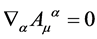 for gauge parameters fulfilling
for gauge parameters fulfilling 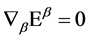 also when
also when  -dependent.
-dependent.
Let us next define the field strength operator 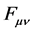 in the usual way
in the usual way
 (18)
(18)
which again can be decomposed consistently w.r.t. . The field strength components
. The field strength components 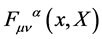 are calculated to be
are calculated to be
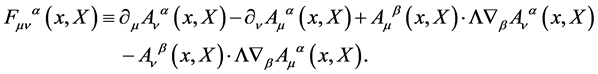 (19)
(19)
Under a local gauge transformation the field strength and its components transform covariantly
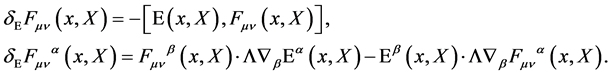 (20)
(20)
As required for algebra elements  and
and 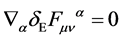 for gauge fields fulfilling
for gauge fields fulfilling 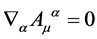 and gauge parameters fulfilling
and gauge parameters fulfilling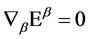 .
.
The above can be viewed as giving rise to a principal bundle P with base space M4, the typical fibre given by the volume-preserving diffeomorphisms 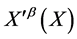 of
of 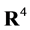 which is identical to the structure group given by
which is identical to the structure group given by . The gauge field
. The gauge field 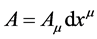 is then the local form of the connection and the field strength
is then the local form of the connection and the field strength
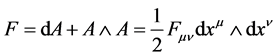 the local form of the curvature of the principal bundle P (M4,
the local form of the curvature of the principal bundle P (M4, ). Locally the mathematical existence of the gauge field and field strength is hence assured. Finally in this paper we do not address questions about the global structure of such a principal bundle.
). Locally the mathematical existence of the gauge field and field strength is hence assured. Finally in this paper we do not address questions about the global structure of such a principal bundle.
Note that no reference to a metric in inner space has been necessary so far.
Turning to the dynamics of the classical gauge theory the Lagrangian for the gauge fields as given in [12] does depend on a metric 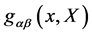 of Minkowskian signature on the inner space
of Minkowskian signature on the inner space  which has been introduced in [12] and discussed there. Under inner coordinate transformations this metric transforms as a contravariant tensor
which has been introduced in [12] and discussed there. Under inner coordinate transformations this metric transforms as a contravariant tensor
 (21)
(21)
In general inner coordinates the Lagrangian is given by [12]
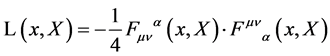 (22)
(22)
and is indeed covariant under the combined gauge transformations Equation (20) and Equation (21). Above, inner indices such as 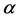 are raised and lowered with
are raised and lowered with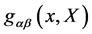 .
.
Excluding any dynamical role for the metric—which we take as an a priori as explained in [12] —we require that the geometry of the inner space is flat, hence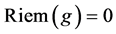 . This means that it is always possible to choose global Cartesian coordinates with the metric
. This means that it is always possible to choose global Cartesian coordinates with the metric 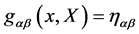 collapsing to the global Minkowski metric
collapsing to the global Minkowski metric 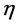 in inner space.
in inner space.
Such choices of coordinates amount to partially fixing a gauge the class of which are the Minkowski gauges [12] . The remaining gauge degrees of freedom leaving 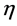 invariant restrict the infinitesimal gauge parameters to the form
invariant restrict the infinitesimal gauge parameters to the form
 (23)
(23)
with 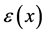 and
and 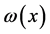 constant in inner space and
constant in inner space and  antisymmetric in
antisymmetric in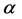 ,
,  which is the (infinitesimal) Poincaré group acting on inner space.
which is the (infinitesimal) Poincaré group acting on inner space.
In Minkowski gauges and Cartesian inner coordinates the Lagrangian is [12] still given by Equation (22) with inner indices such as 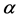 raised and lowered with
raised and lowered with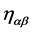 . In such gauges, however, it is only covariant under Poincaré transformations as given in Equation (23) above.
. In such gauges, however, it is only covariant under Poincaré transformations as given in Equation (23) above.
3. Generating Functional for the Green Functions of the Gauge Theory of Volume-Preserving Diffeomorphisms
In this section we establish the starting point for the renormalizability proof of the gauge theory of volume preserving diffeomorphisms in terms of the gauge-fixed generating functional for its quantum Green functions as presented in detail in [13] .
After the review of the classical theory let us turn to the quantum theory and specifically to the generating functional  for the quantum Green functions of the gauge theory of volume-preserving diffeomorphisms given in terms of the gauge fields
for the quantum Green functions of the gauge theory of volume-preserving diffeomorphisms given in terms of the gauge fields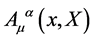 , the ghost and anti-ghost fields
, the ghost and anti-ghost fields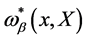 ,
, 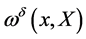 and a matter field
and a matter field 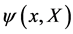 as established in detail in [13]
as established in detail in [13]
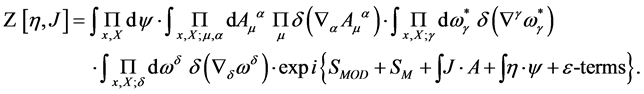 (24)
(24)
The path integrals over the fields are restricted by the 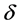 -functions to fields living in the gauge algebra. For the integrals over spacetime and inner space we have chosen the shorthand notation
-functions to fields living in the gauge algebra. For the integrals over spacetime and inner space we have chosen the shorthand notation
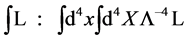 (25)
(25)
which we will keep throughout the rest of the paper and we have dropped the explicit dependence on the coordinates 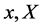 which we will do from now on throughout this paper.
which we will do from now on throughout this paper.
The gauge-fixed action 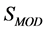 related to the gauge and ghost fields is written in terms of a Lagrangian density
related to the gauge and ghost fields is written in terms of a Lagrangian density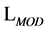
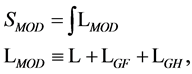 (26)
(26)
where the latter is a sum of the gauge field Lagrangian 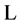 from Equation (22) covariant under the combined gauge transformations Equation (20) and Equation (21), a gauge-fixing term
from Equation (22) covariant under the combined gauge transformations Equation (20) and Equation (21), a gauge-fixing term 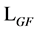 and the ghost field Lagrangian
and the ghost field Lagrangian
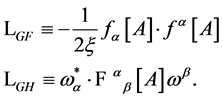 (27)
(27)
In general, the inner indices in Equation (27) are contracted with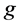 .
.
To represent matter we have added a Dirac field with action
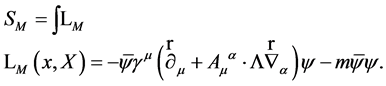 (28)
(28)
Finally we have introduced currents 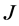 and
and 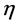 coupled to the gauge and matter fields.
coupled to the gauge and matter fields.
Above 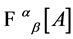 denotes the Faddeev-Popov-DeWitt kernel
denotes the Faddeev-Popov-DeWitt kernel
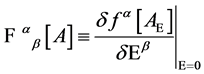 (29)
(29)
belonging to the gauge-fixing functional 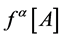 with
with .
.
Note that 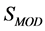 is not invariant under the joint gauge transformations Equations (10) and (17) and Equation (21). As we will see below, however,
is not invariant under the joint gauge transformations Equations (10) and (17) and Equation (21). As we will see below, however, 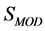 and the quantum theory feature another invariance which is a remnant of the gauge invariance of the classical theory.
and the quantum theory feature another invariance which is a remnant of the gauge invariance of the classical theory.
To be specific in our further analysis let us (i) partially fix the gauge to Minkowski gauges introduced above which preserve the inner metric 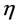 (see Appendix and [12] ) and (ii) fix the remaining gauge degrees of freedom by choosing the Lorentz gauge taking
(see Appendix and [12] ) and (ii) fix the remaining gauge degrees of freedom by choosing the Lorentz gauge taking 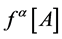 to be
to be
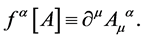 (30)
(30)
The Faddeev-Popov-DeWitt kernel for this choice is easily calculated to be
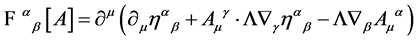 (31)
(31)
and  becomes
becomes
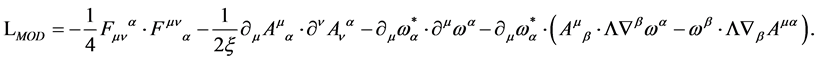 (32)
(32)
Due to (ii) the inner indices in Equation (32) are contracted with 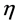 as is the case throughout the rest of the paper.
as is the case throughout the rest of the paper.
Denoting the mass dimension of a field determined as usual by the quadratic part of the Lagrangian by [..] we find
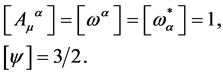 (33)
(33)
Hence, by inspection the Lagrangian above contains products of fields and their spacetime derivatives with mass dimensions four or less only. This ensures renormalizability in the Dyson sense, i.e. counterterms which have to be introduced to absorb spacetime divergences arising in perturbation theory have mass dimensions four or less as well. For the theory to be truly renormalizable, however, these counterterms arising in a perturbation expansion of the generating functional must be shown to take the same form as the above Lagrangian—a task to which we turn next.
Note that we will have to deal with an additional type of divergences in Feynman graphs arising from the generalized sums over inner degrees of freedom. These turn out to be divergent integrals over inner momentum space variables which we will properly define in Section 10.
4. BRST-Type Invariance of Modified Gauge-Fixed Action and of Path Integral Measure Occurring in the Generating Functional for the Quantum Green Functions
In this section we rewrite the generating functional in terms of Nakanishi-Lautrup fields and a new action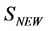 . We then demonstrate the invariance of both
. We then demonstrate the invariance of both  and the path integration measure under a BRST-type symmetry.
and the path integration measure under a BRST-type symmetry.
Let us start with Equation (26)
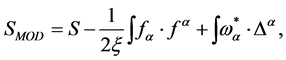 (34)
(34)
where we have introduced the quantity
 (35)
(35)
Re-expressing
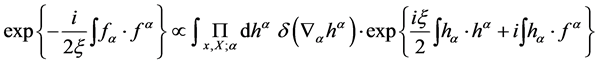 (36)
(36)
in terms of a Gaussian integral over the Nakanishi-Lautrup fields 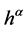 and introducing the corresponding new modified action
and introducing the corresponding new modified action
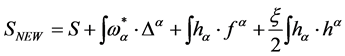 (37)
(37)
the Green functions of the theory are now given as path integrals over the fields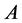 ,
, 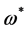 ,
,  ,
,  ,
,  with weight
with weight .
.
By construction the gauge-fixed modified action 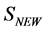 is not invariant under gauge transformations. However, it is invariant under BRST-type transformations parametrized by an infinitesimal fermionic
is not invariant under gauge transformations. However, it is invariant under BRST-type transformations parametrized by an infinitesimal fermionic  anticommuting with ghost and fermionic fields. The BRST-type variations in the theory of volume-preserving diffeomorphisms are given by
anticommuting with ghost and fermionic fields. The BRST-type variations in the theory of volume-preserving diffeomorphisms are given by
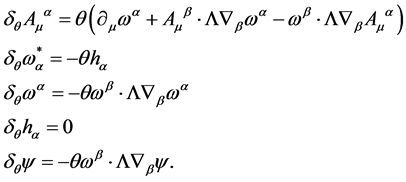 (38)
(38)
The transformations Equation (38) are nilpotent, i.e. if 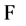 is any functional of
is any functional of ,
, 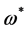 ,
, 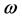 ,
, 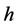 ,
,  and we define
and we define  by
by
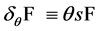 (39)
(39)
then
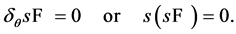 (40)
(40)
The proof for the fields above is straightforward, but somewhat tedious. Here we just sketch the verification of
 (41)
(41)
using the chain-rule and the anticommutativity of  with
with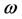 . As a result we have
. As a result we have
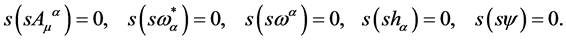 (42)
(42)
The extension to products of polynomials in these fields follows easily [4] .
To verify the BRST invariance of  we note that the BRST transformation acts on functionals of matter and gauge fields as a gauge transformation with gauge parameter
we note that the BRST transformation acts on functionals of matter and gauge fields as a gauge transformation with gauge parameter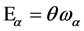 . Hence
. Hence
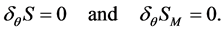 (43)
(43)
Next with the use of Equation (29) we determine the BRST transform of
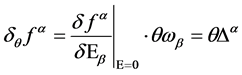 (44)
(44)
which yields
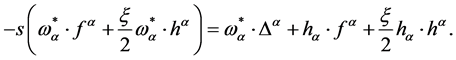 (45)
(45)
Hence we can rewrite
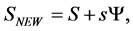 (46)
(46)
where
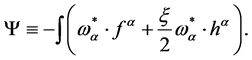 (47)
(47)
Finally it follows from the nilpotency of the BRST transformation
 (48)
(48)
Next let us analyze the path integration measure
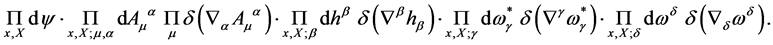 (49)
(49)
Under the BRST-type transformations Equation (38) the Jacobian turns out to be [15]
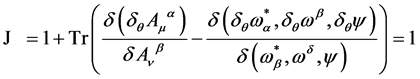 (50)
(50)
as the trace is easily shown to vanish.
In addition the BRST-type transformations Equation (38) respect the divergence-free condition ensuring that the fields live in the gauge algebra
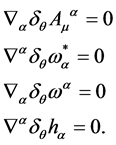 (51)
(51)
As a result the measure Equation (49) is invariant under the BRST-type transformations Equation (38).
5. Symmetries of the Quantum Effective Action and the Zinn-Justin Equation
In this section we derive the Zinn-Justin equation for the gauge theory of volume-preserving diffeomorphisms which follows from the BRST-type invariance of both the modified action 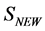 and the path integral measure.
and the path integral measure.
We start with the generating functional for Green functions 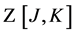 in the presence of additional currents
in the presence of additional currents 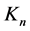 coupled to the nilpotent BRST-type transformations
coupled to the nilpotent BRST-type transformations 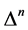 chosing the compact notation
chosing the compact notation
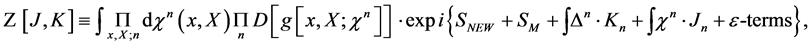 (52)
(52)
where
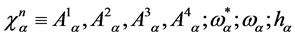 (53)
(53)
denote the gauge and ghost field variables constrained to live in the gauge algebra which is ensured by
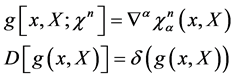 (54)
(54)
and where
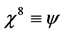 (55)
(55)
denotes the matter field. The BRST-type transformations
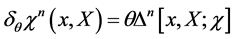 (56)
(56)
act on the various fields as defined by Equation (38)
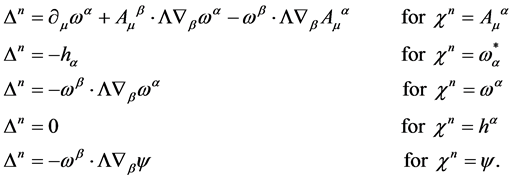 (57)
(57)
As shown in the previous section all: the modified action , the matter action
, the matter action , the nilpotent BRST-transformations
, the nilpotent BRST-transformations  and the path integration measure in
and the path integration measure in  are invariant under the BRST-type transformations Equation (57). Hence we obtain
are invariant under the BRST-type transformations Equation (57). Hence we obtain
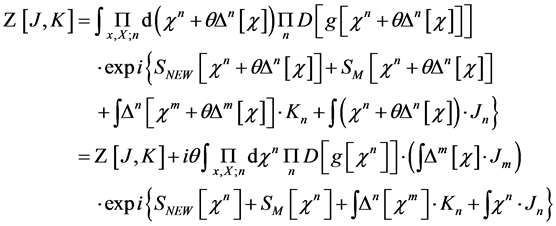 (58)
(58)
which means that the quantum average  in the presence of the currents
in the presence of the currents 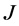 and
and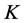
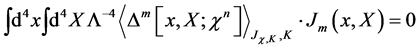 (59)
(59)
vanishes.
Next we define the related quantum effective action in the presence of the current  by
by
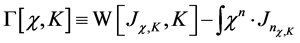 (60)
(60)
with the connected vacuum persistence amplitude  related to
related to 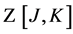 by
by
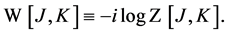 (61)
(61)
Taking the left variational derivative of the effective action w.r.t. a field degree of freedom 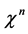 we obtain
we obtain
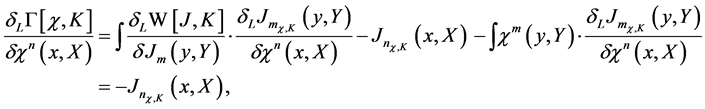 (62)
(62)
where we have made use of the definition of 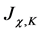 which is the current required to give the fields the expectation value
which is the current required to give the fields the expectation value  in the presence of
in the presence of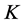
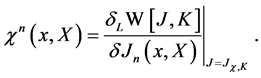 (63)
(63)
Taking next the right variational derivative of the effective action w.r.t. the external current 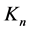 we obtain
we obtain
 (64)
(64)
Finally, inserting both Equation (62) and Equation (64) into Equation (59) we obtain
 (65)
(65)
i.e. the Zinn-Justin equation for the gauge theory of volume-preserving diffeomorphisms.
Defining the antibracket of two functionals  and
and 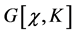 w.r.t. to the field
w.r.t. to the field 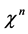 and the current
and the current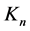
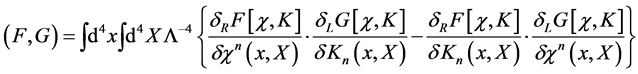 (66)
(66)
the Zinn-Justin equation finally can be re-written in the form
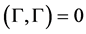 (67)
(67)
as the interchange of 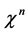 and
and 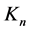 in Equation (65) simply results in a change of sign.
in Equation (65) simply results in a change of sign.
It is this equation which contains the information at the quantum level related to the original gauge symmetry at the classical level which constrains the form of the ultraviolet divergences so that the theory turns out to be renormalizable—the proof of which we turn to next, adapting the general renormalization proof for Yang-Mills theories as outlined e.g. in [4] [15] to our case.
6. Constraints Put on the Perturbative Expansion of the Quantum Effective Action by the Zinn-Justin Equation
In this section we analyze the constraints on the perturbative expansion of the quantum effective action imposed by the Zinn-Justin equation. They result in a combination of the renormalized action  and the infinite part of the
and the infinite part of the 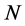 -th loop contribution
-th loop contribution 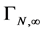 to
to  being invariant under nilpotent transformations related to, but different from the original BRST-type transformations.
being invariant under nilpotent transformations related to, but different from the original BRST-type transformations.
We start by rewriting the action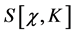
 (68)
(68)
as the sum of a renormalized action 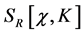 in which masses and coupling constants take their renormalized values and counterterms
in which masses and coupling constants take their renormalized values and counterterms 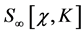 which cancel the infinities from the loop graphs. Both must be invariant under the same symmetries as the original action
which cancel the infinities from the loop graphs. Both must be invariant under the same symmetries as the original action .
.
Next we turn to the quantum effective action 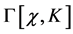 which we perturbatively expand in a series
which we perturbatively expand in a series
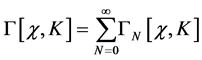 (69)
(69)
where the 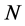 -th order contribution
-th order contribution 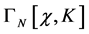 contains both diagrams with
contains both diagrams with 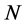 loops as well as diagrams with
loops as well as diagrams with  loops plus counterterms from
loops plus counterterms from 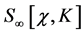 that cancel infinities in graphs with
that cancel infinities in graphs with 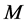 loops, where
loops, where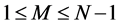 .
.
To prove the renormalizability of the gauge theory of volume-preserving diffeomorphisms it is sufficient to demonstrate that the infinite parts of the  -th order contribution to the quantum effective action display the same terms as the original action
-th order contribution to the quantum effective action display the same terms as the original action . Hence they can be cancelled by counterterms in
. Hence they can be cancelled by counterterms in 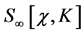 of the same form as the ones in the Lagrangian Equation (37) we have started with.
of the same form as the ones in the Lagrangian Equation (37) we have started with.
To do so we start inserting the perturbation series Equation (69) into the Zinn-Justin Equation (67)
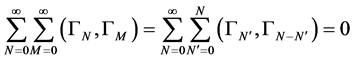 (70)
(70)
which yields for the 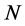 -th order
-th order
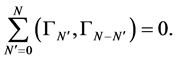 (71)
(71)
We note that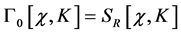 .
.
Next we assume that for all 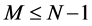 the infinities in all the
the infinities in all the 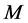 -loop graphs have been cancelled by counterterms in
-loop graphs have been cancelled by counterterms in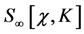 . Infinities in Equation (71) can then only appear in the
. Infinities in Equation (71) can then only appear in the 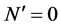 and
and 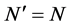 terms which are equal. The infinite part of the condition Equation (71) forces the infinite contribution
terms which are equal. The infinite part of the condition Equation (71) forces the infinite contribution  to
to 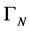 to obey
to obey
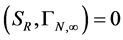 (72)
(72)
the consequences of which we evaluate below.
Before doing so we recall that the action 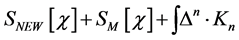 with
with 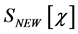 from Equation (37) contains products of fields and their derivatives of dimensionality four or less which guarantees renormalizability in the Dyson-sense, hence counterterms necessary to cancel infinities have dimensionality four or less.
from Equation (37) contains products of fields and their derivatives of dimensionality four or less which guarantees renormalizability in the Dyson-sense, hence counterterms necessary to cancel infinities have dimensionality four or less.
To proceed we next need to establish under which (infinitesimal) symmetry transformations of the action
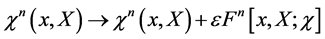 (73)
(73)
the quantum effective action is invariant. To do so we repeat the calculation in Section 5 assuming that all: the modified action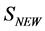 , the matter action
, the matter action ,
, 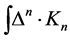 and the path integral measure in
and the path integral measure in 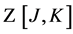 are invariant under the transformation Equation (73).
are invariant under the transformation Equation (73).
Repeating the short calculation performed in Equation (58) yields the general result
 (74)
(74)
For symmetry transformations which are linear in the fields
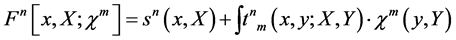 (75)
(75)
with 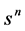 and
and 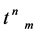 field-independent we further obtain
field-independent we further obtain
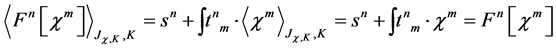 (76)
(76)
which means that the quantum effective action 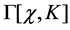 and hence the infinite parts
and hence the infinite parts  in a perturbative expansion are invariant under all the linearly realized symmetry transformations
in a perturbative expansion are invariant under all the linearly realized symmetry transformations
 (77)
(77)
under which the action 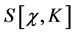 is invariant. These are: spacetime Poincaré transformations (
is invariant. These are: spacetime Poincaré transformations (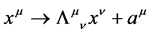 and related field transformations), antighost translations
and related field transformations), antighost translations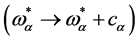 , the ghost phase transformations
, the ghost phase transformations  and—related to the gauge symmetry—global inner Poincaré transformations (
and—related to the gauge symmetry—global inner Poincaré transformations (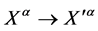 and related field transformations as in Equation (5) with
and related field transformations as in Equation (5) with 
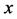 -independent) as well as inner scale transformations (
-independent) as well as inner scale transformations ( and
and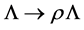 ). We will come back to the scale transformations when discussing restrictions on the regularization of divergent inner momentum integrals.
). We will come back to the scale transformations when discussing restrictions on the regularization of divergent inner momentum integrals.
There are these linearly realized symmetries together with the restriction Equation (72) imposed by the ZinnJustin equation that will be sufficient to determine the general form 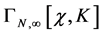 of the infinite part of the quantum effective action.
of the infinite part of the quantum effective action.
Our first step is to use dimensional analysis and ghost number conservation to determine the 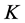 -dependence of
-dependence of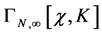 .
.
We denote the mass dimension of a field by [..]. Then for  we find
we find 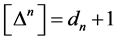 and
and  . Hence,
. Hence,
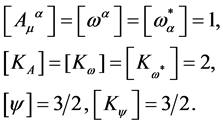 (78)
(78)
As a result the dimension-four quantity  is at most quadratic in the
is at most quadratic in the  and terms quadratic in
and terms quadratic in 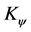 can contain only one additional field of dimension one.
can contain only one additional field of dimension one.
Turning to analyze the impact of ghost number conservation we denote the ghost quantum number of a field by . Then for
. Then for 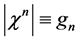 we find
we find  and
and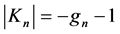 . Hence,
. Hence,
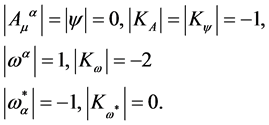 (79)
(79)
This shows that no terms in  quadratic in
quadratic in 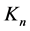 are possible but potentially for
are possible but potentially for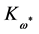 . For that case we note that the BRST-type transformation
. For that case we note that the BRST-type transformation 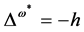 of
of  is linear in the fields, and recalling Equation (64) we find that
is linear in the fields, and recalling Equation (64) we find that
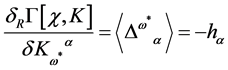 (80)
(80)
is independent of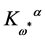 . So
. So 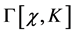 itself is linear in
itself is linear in 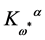 and the infinite part
and the infinite part 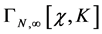 does not depend on
does not depend on  for
for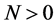 .
.
As a result of this first step we hence have fully determined the 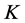 -dependence of
-dependence of 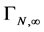 to be
to be
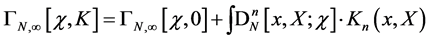 (81)
(81)
introducing the new quantities 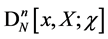 the significance of which will become clear in step two. Before proceeding we recall that
the significance of which will become clear in step two. Before proceeding we recall that
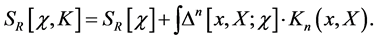 (82)
(82)
Turning to step two we insert Equations (81) and (82) into the Zinn-Justin relation Equation (72). We obtain two constraints to zeroth
 (83)
(83)
and to first order in
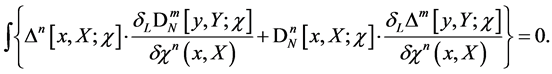 (84)
(84)
To further extract the content of the two constraints above we next define
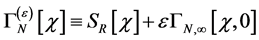 (85)
(85)
and
 (86)
(86)
with 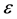 infinitesimal.
infinitesimal.
Then Equation (84) together with the nilpotency of the original BRST-type transformations Equation (57) tells us that the transformations
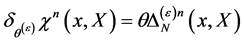 (87)
(87)
are nilpotent as well:
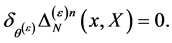 (88)
(88)
And Equation (83) tells us that 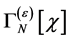 is invariant under the transformations Equation (87):
is invariant under the transformations Equation (87):
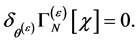 (89)
(89)
These informations will allow us to determine the most general form of both the nilpotent transformations  and of
and of 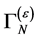 constraining the infinite parts of the quantum effective action sufficiently to prove renormalizability.
constraining the infinite parts of the quantum effective action sufficiently to prove renormalizability.
7. Most General Form of the Quantum BRST-Type Transformations 
In this section we determine the most general form of  which will amount to renormalizing the BRSTtype transformations Equation (57) under which
which will amount to renormalizing the BRSTtype transformations Equation (57) under which  is invariant.
is invariant.
We start noting that the  must have the same linear transformation properties as the
must have the same linear transformation properties as the 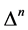 under all: spacetime Poincaré transformations, antighost translations, ghost phase transformations, global inner Poincaré transformations and inner scale transformations. In addition the
under all: spacetime Poincaré transformations, antighost translations, ghost phase transformations, global inner Poincaré transformations and inner scale transformations. In addition the 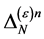 have to be local in the fields and must have the same dimensions as the
have to be local in the fields and must have the same dimensions as the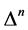 .
.
In the case of the ghost field 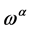 the mass dimensionality of
the mass dimensionality of 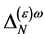 is
is 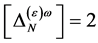 so that the following field combinations could occur in
so that the following field combinations could occur in 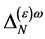 in principle:
in principle: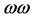 ,
, 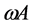 ,
, 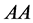 ,
, 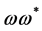 ,
, 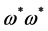 ,
, 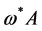 ,
, 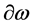 ,
, 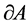 and
and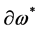 .
.
Checking against the additional requirements that  has to have ghost number
has to have ghost number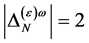 , has to be invariant under inner Lorentz and inner scale transformations and taking into account that the
, has to be invariant under inner Lorentz and inner scale transformations and taking into account that the  anticommute— forcing the addition of a
anticommute— forcing the addition of a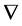 —leaves
—leaves 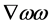 as the only non-vanishing possibility. Hence
as the only non-vanishing possibility. Hence
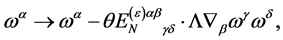 (90)
(90)
with 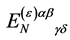 being a constant tensor in inner space, is the most general form of the transformation Equation (87) compatible with the above requirements.
being a constant tensor in inner space, is the most general form of the transformation Equation (87) compatible with the above requirements.
In the case of the gauge field  the mass dimensionality of
the mass dimensionality of 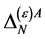 is again
is again 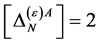 so that the same field combinations as in the ghost field case could occur in
so that the same field combinations as in the ghost field case could occur in 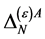 in principle. Checking against the additional requirements that
in principle. Checking against the additional requirements that 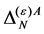 has to have ghost number
has to have ghost number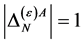 , has to be invariant under all: spacetime, inner Lorentz and inner scale transformations leaves
, has to be invariant under all: spacetime, inner Lorentz and inner scale transformations leaves 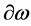 and
and  as the only possibilities. Hence
as the only possibilities. Hence
 (91)
(91)
with  and
and  being constant tensors in inner space, is the most general form of the transformation Equation (87) compatible with the above requirements.
being constant tensors in inner space, is the most general form of the transformation Equation (87) compatible with the above requirements.
In the case of the matter field 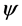 the mass dimensionality of
the mass dimensionality of 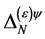 is
is  so that the following field combinations could occur in
so that the following field combinations could occur in 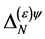 in principle:
in principle: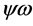 ,
, 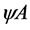 ,
, 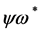 and
and . Checking against the additional requirements that
. Checking against the additional requirements that 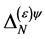 has to have ghost number
has to have ghost number , has to be invariant under inner Lorentz and inner scale transformations leaves
, has to be invariant under inner Lorentz and inner scale transformations leaves 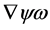 as the only possibility. Hence
as the only possibility. Hence
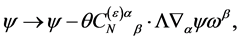 (92)
(92)
with  being a constant tensor in inner space, is the most general form of the transformation Equation (87) compatible with the above requirements.
being a constant tensor in inner space, is the most general form of the transformation Equation (87) compatible with the above requirements.
For the antighost field 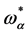 and the Nakanishi-Lautrup field
and the Nakanishi-Lautrup field  the transformations Equation (87) remain trivial so that we find the most general form of
the transformations Equation (87) remain trivial so that we find the most general form of 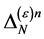 to be
to be
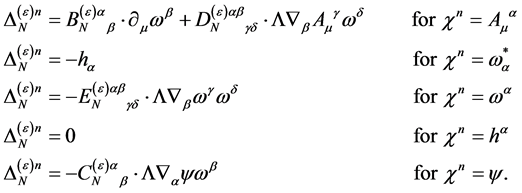 (93)
(93)
Next we turn to working out the implication of the nilpotency condition Equation (88) on the .
.
For the ghost field 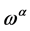 we have to take into account
we have to take into account
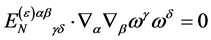 (94)
(94)
which follows from 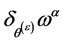 being divergence-free and conclude that
being divergence-free and conclude that
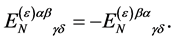 (95)
(95)
To build a constant 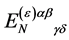 we have the tensor
we have the tensor 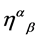 and the pseudo-tensor
and the pseudo-tensor  at hands. As there is parity conservation in inner space we can rule out
at hands. As there is parity conservation in inner space we can rule out 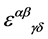 and finally have
and finally have
 (96)
(96)
or
 (97)
(97)
As a result the transformation Equation (93) reduces for the ghost field 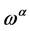 to
to
 (98)
(98)
which is easily found to be nilpotent as required.
For the gauge field 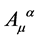 we have to take into account
we have to take into account
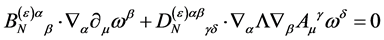 (99)
(99)
which follows from 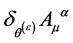 being divergence-free and conclude that
being divergence-free and conclude that
 (100)
(100)
and that
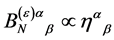 (101)
(101)
as 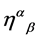 is the only constant tensor of rank 2 available. Parity conservation leaves us with
is the only constant tensor of rank 2 available. Parity conservation leaves us with
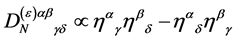 (102)
(102)
or
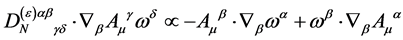 (103)
(103)
so that the transformation Equation (93) reduces for the gauge field 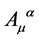 to
to
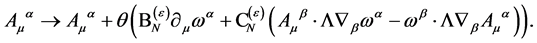 (104)
(104)
Nilpotency requires
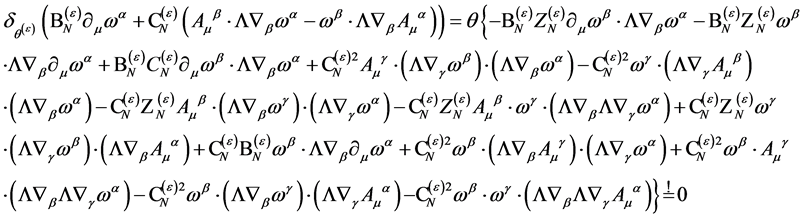 (105)
(105)
which is fulfilled if
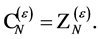 (106)
(106)
Setting
 (107)
(107)
the transformation Equation (93) for the gauge field 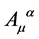 takes the final form
takes the final form
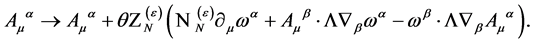 (108)
(108)
For the matter field 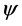 taking into account
taking into account
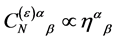 (109)
(109)
the transformation Equation (93) reduces to
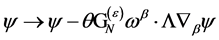 (110)
(110)
which is found to be nilpotent if
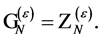 (111)
(111)
As a result we find the most general form of  to be
to be
 (112)
(112)
which amounts to a renormalization of the BRST-type transformations Equation (57) under which  is invariant.
is invariant.
8. Most General Form of  and of the Infinite Parts of the Quantum Effective Action
and of the Infinite Parts of the Quantum Effective Action
In this section we show that the most general form of 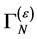 consists of the same terms as the action
consists of the same terms as the action 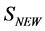 we have started with. This demonstrates that potential infinities related to divergent spacetime integrals at any order of perturbation theory can be reabsorbed in a renormalized action
we have started with. This demonstrates that potential infinities related to divergent spacetime integrals at any order of perturbation theory can be reabsorbed in a renormalized action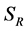 , hence completing the renormalization proof.
, hence completing the renormalization proof.
We start noting that 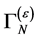 can be written
can be written
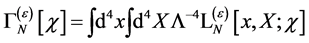 (113)
(113)
in terms of a Lagrangian 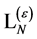 which is local and in which only combinations of the fields and their derivatives with dimensions less or equal to four can occur.
which is local and in which only combinations of the fields and their derivatives with dimensions less or equal to four can occur.
In addition 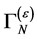 has to be invariant under all the linear transformations
has to be invariant under all the linear transformations 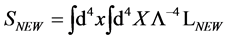 is. Recalling that
is. Recalling that
 (114)
(114)
the action 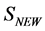 is found to be invariant under spacetime Poincaré transformations, antighost translations, ghost phase transformations, global inner Poincaré transformations and inner scale transformations which has to be true for any matter field action
is found to be invariant under spacetime Poincaré transformations, antighost translations, ghost phase transformations, global inner Poincaré transformations and inner scale transformations which has to be true for any matter field action 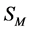 as well.
as well.
Next we turn to establish the most general form of 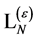 in terms of combinations of fields and their derivatives of dimension four or less, invariant under the above linear transformations and—most importantly—invariant under the modified nilpotent quantum BRST-type transformations Equation (112).
in terms of combinations of fields and their derivatives of dimension four or less, invariant under the above linear transformations and—most importantly—invariant under the modified nilpotent quantum BRST-type transformations Equation (112).
First, the ghost number conservation requires ghosts 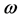 to be paired with antighosts
to be paired with antighosts 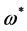 and antighost translation invariance forces antighosts to appear with a derivative
and antighost translation invariance forces antighosts to appear with a derivative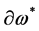 . As the mass dimension
. As the mass dimension 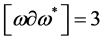
in ghost terms only one more derivative 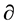 or gauge field
or gauge field 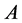 can appear. Hence, the only two ghost combinations fulfilling all conditions are
can appear. Hence, the only two ghost combinations fulfilling all conditions are
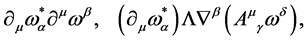 (115)
(115)
where we note that a gauge field 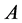 comes together with an inner derivative
comes together with an inner derivative 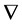 to ensure an even number of inner Lorentz indices.
to ensure an even number of inner Lorentz indices.
Second, the above symmetry constraints require Nakanishi-Lautrup fields  with mass dimension
with mass dimension  to appear in combination with one of the following terms
to appear in combination with one of the following terms ,
,  ,
,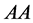 . Hence the only three
. Hence the only three 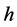 -combinations fulfilling all conditions are
-combinations fulfilling all conditions are
 (116)
(116)
Adding constant tensors so as to combine inner indices to yield scalar expressions in inner space and noting that 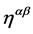 is the only tensor of second rank allowed by the symmetry requirements we then find the most general expression for
is the only tensor of second rank allowed by the symmetry requirements we then find the most general expression for 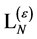 to be
to be
 (117)
(117)
where 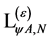 denotes terms containing only combinations of gauge and matter fields and their derivatives of dimension four or less.
denotes terms containing only combinations of gauge and matter fields and their derivatives of dimension four or less.
Variation of 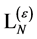 under the modified BRST-type transformations as in Equation (112) yields
under the modified BRST-type transformations as in Equation (112) yields
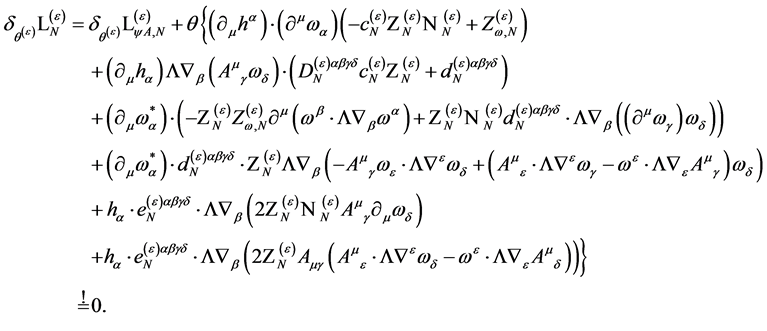 (118)
(118)
The first line above vanishes identically if
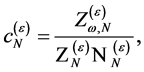 (119)
(119)
the second line if
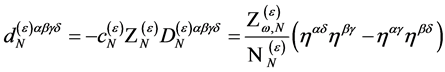 (120)
(120)
and the last two lines if and only if
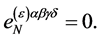 (121)
(121)
Insertion of Equation (120) in the third and fourth lines yields
 (122)
(122)
and in the fifth and sixth lines
 (123)
(123)
as required which leaves us with
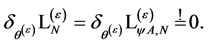 (124)
(124)
Next by inspection of Equation (112) we note that a modified BRST-type transformation acts on the gauge and matter fields exactly in the same way as the original gauge transformation Equation (57) with local gauge parameter
 (125)
(125)
and rescaled inner derivatives
 (126)
(126)
Equation (124) then simply tells us that 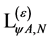 has to be gauge invariant when expressed in terms of rescaled inner derivatives
has to be gauge invariant when expressed in terms of rescaled inner derivatives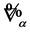 . In addition it contains only combinations of gauge and matter fields and their derivatives of dimension four or less and is invariant under the linear transformations enumerated above. The only gauge field Lagrangian
. In addition it contains only combinations of gauge and matter fields and their derivatives of dimension four or less and is invariant under the linear transformations enumerated above. The only gauge field Lagrangian 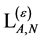 fulfilling these requirements is
fulfilling these requirements is
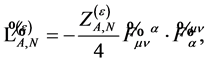 (127)
(127)
where
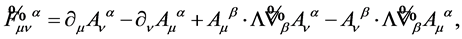 (128)
(128)
and the only matter field Lagrangian 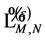 is
is
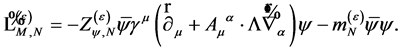 (129)
(129)
As our final result we find the most general 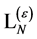 containing only combination of fields and their derivatives of dimensions four or less, being invariant under all: spacetime Poincaré transformations, antighost translations, ghost phase transformations, global inner Poincaré transformations and inner scale transformations and most importantly being invariant under the modified BRST-type transformations Equation (112) to be
containing only combination of fields and their derivatives of dimensions four or less, being invariant under all: spacetime Poincaré transformations, antighost translations, ghost phase transformations, global inner Poincaré transformations and inner scale transformations and most importantly being invariant under the modified BRST-type transformations Equation (112) to be
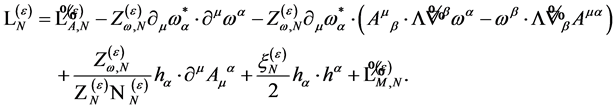 (130)
(130)
Apart from the appearance of a number of new constant coefficients this is exactly the original Lagrangian 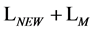 we have started with. By adjusting the
we have started with. By adjusting the 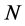 -th order of the unrenormalized constants in the original bare Lagrangian we can absorb
-th order of the unrenormalized constants in the original bare Lagrangian we can absorb 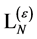 so that
so that  and
and 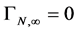 which completes the renormalizability proof of the gauge theory of the volume-preserving diffeomorphism group.
which completes the renormalizability proof of the gauge theory of the volume-preserving diffeomorphism group.
9. Feynman Rules in the Lorentz Gauge
In this section we derive the Feynman rules for the gauge theory of volume-preserving diffeomorphisms in the Lorentz gauge as a prerequisite to establish viable regularization schemes for the divergent inner momentum integrals occurring in a loop expansion of the quantum effective action.
In order to analyze the structure of inner momentum space integrals at any order of a loop-wise expansion of the quantum effective action we turn to Feynman diagrams. Hence we need to derive the momentum space Feynman rules for the Lagrangian  for gauge and ghost fields in the Lorentz gauge as in Equation (32) omitting matter contributions for the sake of simplicity because they do not add new features to the present discussion.
for gauge and ghost fields in the Lorentz gauge as in Equation (32) omitting matter contributions for the sake of simplicity because they do not add new features to the present discussion.
As usual we split 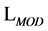 into a free Lagrangian
into a free Lagrangian 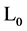 and an interaction Lagrangian
and an interaction Lagrangian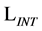 .
.
The free Lagrangian 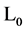 for the gauge and ghost fields
for the gauge and ghost fields
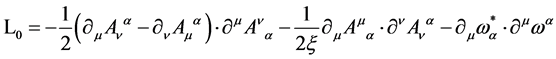 (131)
(131)
can by partial integration be easily brought into the usual quadratic form
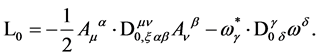 (132)
(132)
Above we have introduced the non-interacting gauge and ghost field fluctuation operators
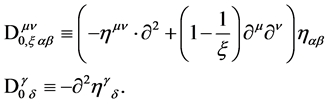 (133)
(133)
The corresponding free propagators 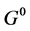 are defined through
are defined through
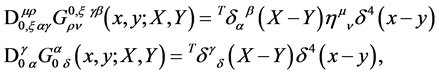 (134)
(134)
where
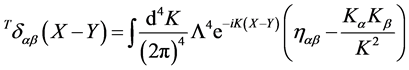 (135)
(135)
is the scale-invariant delta function transversal in inner space which is compatible with the constraint that both the gauge and the ghost fields are divergence-free in inner space. Note that the transversal delta-function 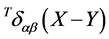 naturally arises from canonical quantization using Dirac brackets [3] .
naturally arises from canonical quantization using Dirac brackets [3] .
After a little algebra we find the momentum space gauge and ghost field propagators to be
 (136)
(136)
Note that both propagators are transversal in inner space and that they reduce to 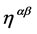 when acting on currents which are divergence-free in inner space. As all currents are in fact divergence-free in inner space the inner degrees of freedom do not propagate and we can replace the projection in specific calculations by
when acting on currents which are divergence-free in inner space. As all currents are in fact divergence-free in inner space the inner degrees of freedom do not propagate and we can replace the projection in specific calculations by
 (137)
(137)
Note that the spacetime parts of the propagators equal the usual Yang-Mills propagators.
Next we calculate the various vertices related to the interaction Lagrangian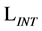 .
.
We start with the tri-linear gauge field self-coupling term
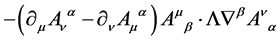 (138)
(138)
corresponding to a vertex with three vector boson lines. If these lines carry incoming spacetime momenta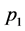 ,
, 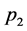 ,
,  , inner momenta
, inner momenta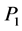 ,
, 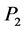 ,
, 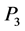 and gauge field indices
and gauge field indices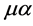 ,
,  ,
,  the contribution of such a vertex to a Feynman graph is
the contribution of such a vertex to a Feynman graph is
 (139)
(139)
with
 (140)
(140)
The quadri-linear gauge field self-coupling term
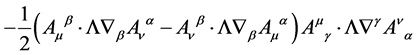 (141)
(141)
corresponds to a vertex with four vector boson lines. If these lines carry incoming spacetime momenta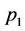 ,
, 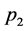 ,
, 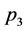 ,
, 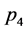 , inner momenta
, inner momenta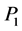 ,
, 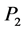 ,
, 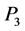 ,
, 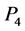 and gauge field indices
and gauge field indices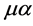 ,
, 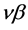 ,
, 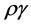 ,
, 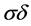 the contribution of such a vertex to a Feynman graph is
the contribution of such a vertex to a Feynman graph is
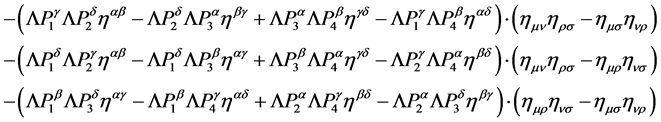 (142)
(142)
with
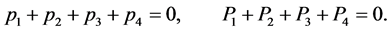 (143)
(143)
Finally, the gauge-ghost field coupling term
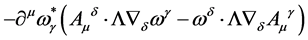 (144)
(144)
corresponds to a vertex with one outgoing and one incoming ghost line as well as one vector boson line. If these lines carry incoming spacetime momenta ,
, 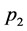 ,
, 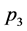 , inner momenta
, inner momenta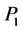 ,
, 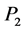 ,
,  and field indices
and field indices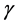 ,
, 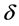 ,
, 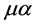 the contribution of such a vertex to a Feynman graph becomes
the contribution of such a vertex to a Feynman graph becomes
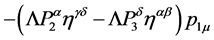 (145)
(145)
with
 (146)
(146)
In summary, the above propagators and vertices allow us to perturbatively evaluate the quantum effective action of the theory in a loop-wise expansion. In addition they are manifestly covariant w.r.t. spacetime Poincaré transformations and related to the gauge symmetry-global inner Poincaré transformations. Most importantly they are invariant under inner scale transformations (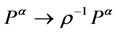 and
and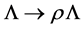 ). The latter invariance is manifest as each factor of
). The latter invariance is manifest as each factor of 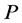 comes together with a
comes together with a 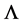 and
and 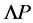 is scale-invariant.
is scale-invariant.
Note that for any Feynman graph the analogon of the sums over Lie algebra structure constants in Yang-Mills theories in the theory under consideration are integrals over inner momentum space variables.
10. Regularization of the Divergent Inner Momentum Integrals
In this section we show that 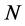 -loop inner momentum integrals arising in the expansion of the quantum effective action factorize into sums of
-loop inner momentum integrals arising in the expansion of the quantum effective action factorize into sums of 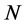 products of one-loop inner momentum integrals. As a key result we find that any regularization procedure for the divergent one-loop inner momentum integrals compatible with the symmetries of the quantum effective action results in a perturbatively well defined quantum field theory. Finally we specify one such regularization procedure.
products of one-loop inner momentum integrals. As a key result we find that any regularization procedure for the divergent one-loop inner momentum integrals compatible with the symmetries of the quantum effective action results in a perturbatively well defined quantum field theory. Finally we specify one such regularization procedure.
According to the Feynman rules stated in Section 9 vertices contribute simple monomials in the inner momenta to a Feynman graph so that inner momentum space integrals occurring in the 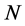 -th loop contribution to the perturbative expansion of the quantum effective action factorize into terms of the form
-th loop contribution to the perturbative expansion of the quantum effective action factorize into terms of the form
 (147)
(147)
where  denote the inner Lorentz indices of the inner momenta
denote the inner Lorentz indices of the inner momenta 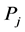 appearing in the
appearing in the  -th loop integral
-th loop integral
 with
with 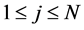 and
and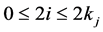 . Note that only integrals with an even number of
. Note that only integrals with an even number of 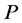 do not vanish.
do not vanish.
As these  -loop inner momentum integrals factorize into sums of
-loop inner momentum integrals factorize into sums of 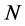 products of one-loop inner momentum integrals it is sufficient to evaluate integrals of the form
products of one-loop inner momentum integrals it is sufficient to evaluate integrals of the form
 (148)
(148)
Above we have extracted the Lorentz structure 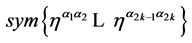 from the integral which is a totally symmetric tensor given in terms of the inner Minkowski metric
from the integral which is a totally symmetric tensor given in terms of the inner Minkowski metric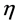 .
.
The remaining scale-invariant integrals are of the form
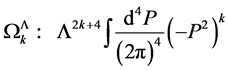 (149)
(149)
where the subscript 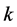 counts powers of
counts powers of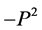 . These divergent
. These divergent 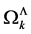 correspond to the eigenvalues of the Casimir operators of the gauge algebra in Yang-Mills theories.
correspond to the eigenvalues of the Casimir operators of the gauge algebra in Yang-Mills theories.
Before turning to the regularization of the 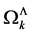 we note that the
we note that the 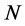 -loop contribution Equation (147) to the perturbative expansion of the quantum effective action can be rewritten in terms of the
-loop contribution Equation (147) to the perturbative expansion of the quantum effective action can be rewritten in terms of the 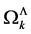 as
as
 (150)
(150)
Hence, to get a well defined theory it is sufficient to find a regularization procedure for the 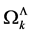 that is compatible with the symmetries of the quantum effective action, i.e. is invariant under inner Poincaré transformations as well as inner scale transformations.
that is compatible with the symmetries of the quantum effective action, i.e. is invariant under inner Poincaré transformations as well as inner scale transformations.
Stated differently each regularization procedure for the 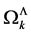 that is compatible with the symmetries of the quantum effective action yields a well-defined quantum field theory belonging to the classical gauge theory of volume-preserving diffeomorphisms.
that is compatible with the symmetries of the quantum effective action yields a well-defined quantum field theory belonging to the classical gauge theory of volume-preserving diffeomorphisms.
Next we turn to specifing one such regularization procedure compatible with the symmetries of the quantum effective action. This will be done in three steps. In the first step we will slice the inner momentum Minkowski space into light-like, time-like and space-like shells of invariant lengths, in the second we will discard the space-like shells and in the third we will invariantly regularize the remaining integral over lightand time-like shells making use of the existence of an arbitrary point mass and its rest frame.
Slicing the inner Minkowski space in the first step into light-like, time-like and space-like shells of invariant lengths 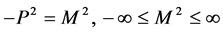 which are invariant under proper Lorentz transformations of the inner momentum space we can identically rewrite
which are invariant under proper Lorentz transformations of the inner momentum space we can identically rewrite
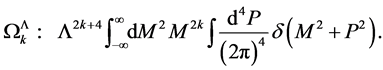 (151)
(151)
Second, to regularize 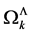 in a Lorentz-invariant way we cut off the space-like shells with negative lengths
in a Lorentz-invariant way we cut off the space-like shells with negative lengths  and split
and split 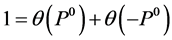 so that
so that
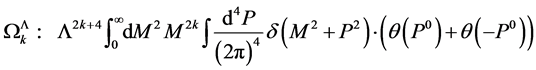 (152)
(152)
which is a Lorentz-invariant procedure. This cutoff of space-like shells arises naturally from the condition of positivity for the Hamiltonian for the gauge and ghost fields as derived in [12] which restricts all fields Fouriertransformed over inner space to have support on the set , where
, where
 (153)
(153)
denote the forward and backward light cones in inner momentum space.
Third, we can always assume the existence of a point mass which is at rest in some Lorentz frame. In that frame we can define a time-like vector 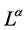 setting
setting 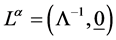 which has invariant length
which has invariant length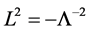 . Then for all
. Then for all 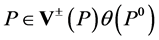 can be rewritten in an Lorentz invariant way
can be rewritten in an Lorentz invariant way
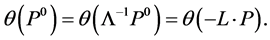 (154)
(154)
In addition
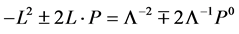 (155)
(155)
again for all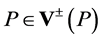 .
.
This allows us to define 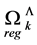 as a scale-invariant integral over the forward cone
as a scale-invariant integral over the forward cone 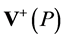 with a cutoff for
with a cutoff for
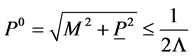 and over the backward cone
and over the backward cone 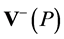 with a cutoff for
with a cutoff for 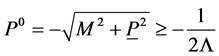 for fixed
for fixed 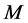 first and then summing over all
first and then summing over all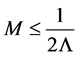
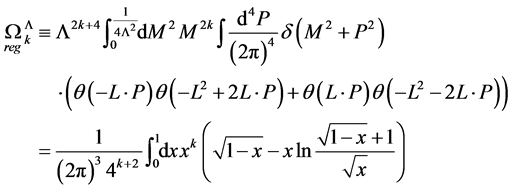 (156)
(156)
which is a positive, finite and manifestly scale-invariant Lorentz scalar for all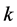 . Explicitly we find
. Explicitly we find
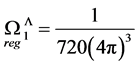 which corresponds to the eigenvalue of the quadratic Casimir operator in Yang-Mills theories occurring e.g. in the one-loop beta function of the pure gauge theory as calculated for the present case in [13]
which corresponds to the eigenvalue of the quadratic Casimir operator in Yang-Mills theories occurring e.g. in the one-loop beta function of the pure gauge theory as calculated for the present case in [13]
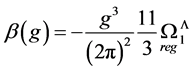 (157)
(157)
demonstrating its asymptotic freedom as well as in the beta function of the theory including all SM fields
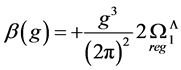 (158)
(158)
which shows that within the SM the gauge quanta are not confined and hence observable.
This completes the proof that the gauge theory of volume-preserving diffeormorphisms can be consistently quantized and turned into a well-defined quantum field theory. In fact we should rather say into a family of welldefined quantum field theories which differ by the choice of regularization procedure for the inner momentum integrals.
11. Conclusions
In this paper we have established that the gauge theory of volume-preserving diffeomorphisms of an inner fourdimensional space, which arises naturally from the assumption that inertial and gravitational mass need not be the same for virtual quantum states, can be consistently quantized and turned into a well-defined quantum field theory or rather into a family of well-defined quantum field theories which differ by the choice of regularization procedure for the inner momentum integrals.
To get there we have first shown that the gauge-fixed action and the path integral measure occurring in the generating functional for the quantum Green functions of the theory obey a BRST-type symmetry. This has allowed us next to demonstrate that the quantum effective action fulfils a Zinn-Justin-type equation which limits the infinite parts of the quantum effective action to have the same form as the gauge-fixed Lagrangian of the theory proving its spacetime renormalizability. Finally based on the theory’s Feynman rules we have shown that the divergent inner space integrals related to the gauge group’s infinite volume are regularizable in a way consistent with the symmetries of the theory. In this context it is worth noting that as a byproduct viable quantum gauge field theories are not limited to finite-dimensional compact gauge groups as is commonly assumed.
Finally: what has all of this to do with gravity? To answer this question we have analysed the classical limit 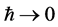 of the gauge theory of volume-preserving diffeomorphisms coupled to a matter field. In that process the inner space collapses, the field dependence on inner coordinates disappears and so does the symmetry under volume-preserving diffeomorphisms of the inner space. On the other hand a new symmetry group emerges: the group of coordinate transformations of four-dimensional spacetime and with it General Relativity coupled to a point particle [16] . Hence, as is necessary for the interpretation of the present theory as a quantum theory of gravity, GR emerges as its classical limit.
of the gauge theory of volume-preserving diffeomorphisms coupled to a matter field. In that process the inner space collapses, the field dependence on inner coordinates disappears and so does the symmetry under volume-preserving diffeomorphisms of the inner space. On the other hand a new symmetry group emerges: the group of coordinate transformations of four-dimensional spacetime and with it General Relativity coupled to a point particle [16] . Hence, as is necessary for the interpretation of the present theory as a quantum theory of gravity, GR emerges as its classical limit.
This result implies then that the SM of particle physics can be completed to contain the gravitational interaction at the quantum level as well.
Practically one starts with the renormalizable action for the SM [4] [5] [8]
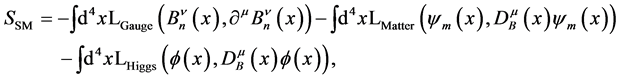 (159)
(159)
where for the sake of clarity we reinsert the arguments  (and
(and  below as well) on which the fields depend. Above
below as well) on which the fields depend. Above 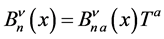 denote the
denote the 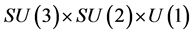 gluon and electro-weak gauge fields decomposed in terms of their Lie algebra generators
gluon and electro-weak gauge fields decomposed in terms of their Lie algebra generators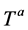 ;
;  denote the quark and lepton fields occurring in three generations and
denote the quark and lepton fields occurring in three generations and 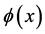 the Higgs field. Finally
the Higgs field. Finally
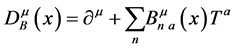 (160)
(160)
denotes the covariant derivative in a suitable gauge algebra representation.
To get the SM coupled to gravity, in short SM + G, we only have to endow each SM field with inner space coordinates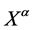
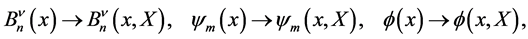 (161)
(161)
introduce the gauge field  as in Section 2 and the corresponding covariant derivative
as in Section 2 and the corresponding covariant derivative
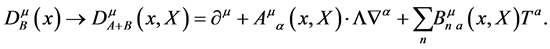 (162)
(162)
The renormalizable action for the SM + G is then simply
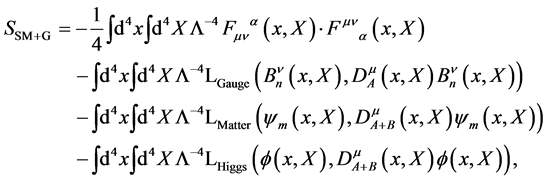 (163)
(163)
where the first term is the gauge field action Equation (22). All amplitudes or other expressions related to observable quantities calculated within the SM + G obviously have to be evaluated in the physical limit as discussed in [14] .
It is reassuring that not only the microscopic strong and electro-weak interactions can be described within a renormalizable quantum gauge field theory framework formulated on a priori flat spacetime. In fact gravity at the quantum level can be described by following exactly the same logic, however, the theory gets more complicated due to its non-compact gauge group having an infinite volume. Yet it is still renormalizable. So nature seems to allow for a consistent, rupture-free picture based on conservation laws and symmetry considerations at least up to energy scales far beyond experimental reach.
Finally, new physics may derive from Equation (163), for example in the realm of cosmology and the early universe where new light might be shed on unsolved questions arising e.g. around dark energy [17] . For sure the quantum gauge field  has left its imprints on the early universe e.g. in a gravitational form of the cosmic background radiation which, however, will not obey the simple Planck distribution its electromagnetic cousin does due to the self-interaction of the gravitational field and its asymptotic freedom nature in the absence of other fields.
has left its imprints on the early universe e.g. in a gravitational form of the cosmic background radiation which, however, will not obey the simple Planck distribution its electromagnetic cousin does due to the self-interaction of the gravitational field and its asymptotic freedom nature in the absence of other fields.
Appendix: Notations and Conventions
Generally, (M4,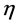 ) denotes the four-dimensional Minkowski space with metric
) denotes the four-dimensional Minkowski space with metric , small letters denote space-time coordinates and parameters and capital letters denote coordinates and parameters in inner space.
, small letters denote space-time coordinates and parameters and capital letters denote coordinates and parameters in inner space.
Specifically, 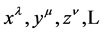 denote Cartesian spacetime coordinates. The small Greek indices
denote Cartesian spacetime coordinates. The small Greek indices 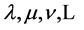 from the middle of the Greek alphabet run over
from the middle of the Greek alphabet run over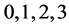 . They are raised and lowered with
. They are raised and lowered with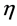 , i.e.
, i.e. 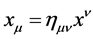 etc. and transform covariantly w.r.t. the Lorentz group
etc. and transform covariantly w.r.t. the Lorentz group . Partial differentiation w.r.t. to
. Partial differentiation w.r.t. to 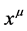 is denoted by
is denoted by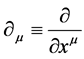 .
.
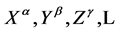 denote inner Cartesian coordinates we can always choose by partially fixing the gauge to socalled Minkowski gauges [12] . The small Greek indices
denote inner Cartesian coordinates we can always choose by partially fixing the gauge to socalled Minkowski gauges [12] . The small Greek indices 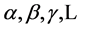 from the beginning of the Greek alphabet run again over
from the beginning of the Greek alphabet run again over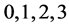 . They are raised and lowered with
. They are raised and lowered with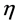 , i.e.
, i.e. 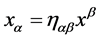 etc. and transform covariantly w.r.t. the inner Lorentz group
etc. and transform covariantly w.r.t. the inner Lorentz group . Partial differentiation w.r.t. to
. Partial differentiation w.r.t. to 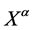 is denoted by
is denoted by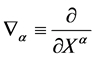 .
.
The same lower and upper indices are summed unless indicated otherwise.