A Simple Deconstruction of the HadCRU Global-Mean Near-Surface Temperature Observations ()
1. Introduction
Since 1994 we have published four scientific papers wherein we used Singular Spectrum Analysis (SSA) to analyze up to four observational records of global-mean near-surface temperature. In those papers, the SSA results were obtained as if from a statistical “black box”, that is, all at once and not intimately connected to the observed temperatures. Here we remedy this by connecting the SSA results to the observed temperatures. We will do this systematically, step by step. In particular we will use Simple Moving Averages (SMAs) of different time periods to reveal an aspect of the observed temperatures. We will compare this aspect to what SSA shows more completely. In this way we will link the features revealed by SSA directly to the temperature observations. As we do this with each SSA feature, we will subtract it from the observed temperatures and then apply another SMA to reveal the next aspect of the observed temperatures.
In our two most-recent papers on this matter, “Causes of the Global Warming Observed Since the 19th Century” ([1]; hereafter Causes) and “A Fair Plan to Safeguard Earth’s Climate: 3. Outlook for Global Temperature Change Throughout the 21st Century” ([2]; hereafter FP3), we applied SSA to four observational datasets of global-mean near-surface temperature: 1) the Hadley Centre-Climate Research Unit (HadCRU) located in the United Kingdom, with data starting in 1850 [3]; 2) the National Climate Data Center of the US National Oceanographic and Atmospheric Administration (NOAA) located in Asheville, North Carolina, with data starting in 1880 [4]; 3) the Goddard Institute of Space Studies of the US National Aeronautics and Space Administration (NASA) located in New York City, with data starting in 1880 [5]; and 4) the Japanese Meteorological Agency (JMA) located in Tsukuba, Japan, with data starting in 1891 [6, 7]. In FP3 we showed that the starting years of datasets 2-4 are too late to properly characterize the structure of the first Quasi-periodic Oscillation, QPO-1, revealed by the earlier starting date of dataset 1. Accordingly, here we restrict attention to the HadCRU temperature dataset alone.
2. Results
Here we present results for the trend in the observations, the three Quasi-periodic Oscillations (QPOs) that are predictable year to year, and the remaining variations that are not predictable year to year. We represent the latter by a Gaussian probability distribution (GPD).
2.1. The Trend
The HadCRU observed global-mean near-surface temperatures from 1850 through 2012 are shown in Figure 1(a). It can be seen that there is considerable information in this record, both with long and short periods. To reveal this more clearly, let’s use a Simple Moving Average (SMA) given mathematically by
 (1)
(1)
with N an odd number. We restrict N to be odd so that the year at which the SMA is located is an integer. For example, for N = 21, the year at which the SMA is located is 11, with 10 data points to both the left and right thereof. If N were 20, then the year of the SMA would be 10.5. Since this is not a year in the dataset, we would have to place the SMA at either 10 or 11. Because we will calculate the Pearson Coefficient of Determination (R2) of the SMA with results from the SSA, our using an even N would result in slightly different values for the two possible locations for the SMA, and thus two possible different values of R2. We avoid this by restricting N to be odd. Of course it is well known that such SMA has deficiencies in terms of its frequency response [8], but we use it here anyway because of its simplicity and, thus, transparency.
The result of using SMA with N = 21 is shown by the blue line in Figure 1(b). It can be seen that the shortperiod fluctuations have been removed by the 21-year SMA, thereby revealing the trend in the observed temperatures plus an oscillation of approximately 60 years duration. We first focus on the trend and then on the os-

Figure 1. (a) The observed global-mean near-surface temperature departures from the 1961-1990 average; (b) As in (a), but with the 21-year Simple Moving Average shown by the blue line; (c) As in (a), but with a 61-year Simple Moving Average shown by the purple line; (d) As in (c), but with the SSA trend shown by the red line.
cillation. To do this we apply a 61-year SMA to the observations of panel a, that is, we use Equation (1) with N = 61 years rather than 21 years. Of course in our so doing we “lose” the first and last 30 years of the observations, just as we “lost” the first and last 10 years of the observations when we used the 21-year SMA. This is another drawback of SMA, a drawback that is not suffered by SSA, as we shall see.
The purple curve in Figure 1(c) shows the result of the 61-year SMA. Here all the oscillations have been removed to reveal the trend, albeit only over the 163 – 2 × 30 = 103 central years of the record. The red line in Figure 1(d) shows the trend revealed by SSA. This trend, which comes from the SSA “black box”, is essentially identical to the trend revealed by the 61-year SMA. In fact we chose the 61-year period by calculating the Pearson Coefficient of Determination, R2, of the SMA data with the SSA trend for several odd values of N, and selecting the one that gives the largest R2. As shown in Table 1, R2 = 0.999 for N = 61 years. In other words, the SSA trend is the same as the trend given by the 61-year SMA, but extended backward in time by 30 years to the beginning of the observations in 1850, and forward in time to the latest observation in 2012. Accordingly, there is nothing mysterious about the SSA trend.
As we showed in Causes, the SSA trend is due to humanity—not nature—as a result of our emissions of greenhouse gases (carbon dioxide, methane, nitrous oxide and the chloroflurocarbons), aerosol precursors (sulfur dioxide, black carbon and organic carbon), and land-use changes (predominantly through deforestation).
2.2. QPO-1
We now investigate the long-period Quasi-periodic Oscillation in the observations. We do so by subtracting the SSA trend shown by the red curve in Figure 1(d) from the observed temperature departures shown by the black curve therein. The result is shown in Figure 2(a). These detrended observations reveal not only the long-period QPO, but the shorter period QPOs and stochastic noise as well. Accordingly, we apply a 21-year SMA given by Equation (1) with N = 21 to the detrended observations shown in Figure 2(a). The result is the blue curve shown in Figure 2(b), wherein the first and last 10 years of the detrended observations are “lost” due to the 21-year SMA. The long-period variation is now clearly seen. In Figure 2(c) the SSA QPO-1 is shown by the red curve. It is seen that SSA QPO-1 is almost identical to the blue curve also shown in Figure 2(c). We chose the length of the SMA to be 21 years because it maximizes the R2 with QPO-1, yielding a value of 0.991, as shown in Table 1. Thus SSA QPO-1 is what one obtains from an SMA of

Figure 2. (a) The detrended observed global-mean near-surface temperature departures from the 1961-1990 average; (b) As in (a), but with a 21-year Simple Moving Average shown by the blue line; (c) As in (b), but with QPO-1 shown by the red line; (d) QPO-1 shown by the red line and its fit by y(t) = C + A sin [2π(t – 1850)/P – ], with C, A, P and
], with C, A, P and  shown in Table 1, shown by the black line.
shown in Table 1, shown by the black line.
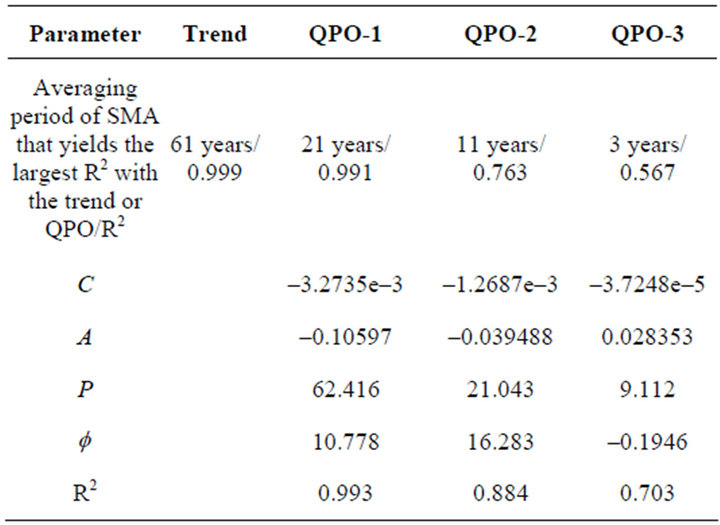
Table 1. Averaging period of the Simple Moving Average that yields the largest coefficient of determination (R2) with the SSA trend and QPOs 1, 2 and 3, together with the R2 thereof. Values of the parameters of the sine-wave representations, y(t) = C + A sin [2π(t – 1850)/P – ], and coefficients of determination (R2), for QPO’s 1, 2 and 3 for the HadCRU observed temperature dataset.
], and coefficients of determination (R2), for QPO’s 1, 2 and 3 for the HadCRU observed temperature dataset.
21-years applied to the detrended observations, except that SSA extends backward to 1850 and forward to 2012. Accordingly, there is nothing mysterious about QPO-1 given by the SSA “black box”. In fact, it is the QPO that we discovered in our 1994 paper “An Oscillation in the Global Climate System of Period 65-70 Years” ([9]; hereafter Discovery) using SSA; it has come to be known as the Atlantic Multidecadal Oscillation, or AMO. QPO-1 is most likely caused by the natural variation of the thermohaline circulation [10].
As shown in Figure 2(d), QPO-1, aka the AMO, is sufficiently regular in period and amplitude that it can be represented quite well by a sine wave, with a Coefficient of Determination R2 = 0.993. The characteristics of this sine-wave fit are shown in Table 1. It is seen that the period and amplitude are 62.4 years and 0.11˚C, respectively. Accordingly, QPO-1 is the dominant natural variation in the HadCRU observations.
2.3. QPO-2
Subtracting QPO-1 from the detrended temperature observations yields the record shown in Figure 3(a). It is evident that this record contains at least one additional QPO. We can show this by applying Equation (1) to the data with N = 11. The result is shown by the blue line in Figure 3(b). Here an irregular oscillation is seen with a period close to 20 years. The result given by SSA is shown by the red curve of Figure 3(c). This is QPO-2. The 11-year length of the SMA was chosen to maximize the Coefficient of Determination with QPO-2, yielding a value of R2 = 0.763, as shown in Table 1. Thus the 11-year SMA is a reasonably good indicator of QPO-2. As for QPO-1, QPO-2 determined by SSA is smoother and more regular than the result given by SMA with N = 11. Moreover, SSA defines QPO-2 for all 163 years of the observed temperature record, while SMA loses the first and last 5 years thereof.
QPO-2 was discovered by Ghil and Vautard [11] and also found by us in our Discovery paper. No definitive cause for QPO-2 has yet been found [12].
While QPO-2 is less regular than QPO-1, it too can be fit by a sine wave as shown in Figure 3(D) and Table 1. It is seen that the period and amplitude are 21.0 years and 0.04˚C, respectively, with a Coefficient of Determination R2 = 0.884.
2.4. QPO-3
Subtracting QPO-2 from the detrended temperature observations minus QPO-1 yields the record shown in Figure 4(a). It appears therefrom that there is least one additional QPO therein. We can show this by applying Equation (1) to the data with N = 3. The result is shown by the blue line in Figure 4(b). Here an irregular oscillation is seen with a period close to 10 years. The result given by SSA is shown by the red curve of Figure 4(c). This is QPO-3. The 3-year length of the SMA was chosen to maximize the Coefficient of Determination with QPO-3, yielding a value of R2 = 0.567, as shown in Table 1. Thus the 3-year SMA is an indicator of QPO-3, but it is not as good an indicator as the SMA with N = 11 years is of QPO-2, and it is much worse than the SMA with N = 61 years is of QPO-1. This indicates that we have gone as far as we can go in representing the QPOs of the HadCRU temperature record by an SMA. Nevertheless, we can represent QPO-3 by a sine wave as shown in Figure 4(d). As shown in Table 1, this yields a period of 9.1 years, an amplitude of 0.03˚C and R2 = 0.703.
QPO-3 was discovered by Ghil and Vautard [11] and also found by us in our Discovery paper. As for QPO-2, no definitive cause for QPO-3 has yet been found [12].
2.5. The Unpredictable Natural Variability
Figure 5(a) shows the detrended observations minus QPOs 1, 2 and 3. While there are additional QPOs in these data [12], they are too irregular in amplitude and/or period to be represented by a sine wave. Thus, these QPOs are not predictable on a year-to-year basis. Accordingly we represent them and the additional stochastic noise therein not by a sine wave, but rather by a probability distribution. Figure 5(b) shows the Cumulative Distribution Function (CDF) for the data in Figure 5(a). The vertical axis on this plot is the Error Function of the horizontal axis. Since the integral of a Gaussian probability distribution (GPD) is an Error Function, a straight line on this plot reveals a probability distribution that is