An Inexact Implementation of Smoothing Homotopy Method for Semi-Supervised Support Vector Machines ()
1. Introduction
In the field of machine learning, it’s essential to collect a large amounts of labeled data for the purpose of training learning algorithms. However, for many applications, huge number of data can be cheaply collected, but manual labeling of them is often a slow, expensive and error-prone process. It’s desirable to utilize the unlabeled data points for the implementation of the learning task. The goal of semi-supervised classification is to employ the large collection of unlabeled data jointly with a few labeled data to finish the task of classification and prediction [11,18].
Semi-supervised support vector machines (S3VMs) is an appealing method for the semi-supervised classification. In [7], K.P. Bennett et al. first formulated it as a mixed integer programming such that some state-ofthe-art softwares can handle the formulation. Since that, a large number of methods have been applied to solve the non-convex optimization problem associated with S3VMs, such as convex-concave procedures [5], non-differntiable methods [1], gradient descent method [13], continuation technique [12], branch-and-bound algorithms [7,14], and semi-definite programming [17] etc. A survey of these methods can be seen from [11,18].
As pointed out in [12], one reason for the large number of proposed algorithms for S3VMs is that the resulting optimization problem is non-convex that generates local minima. Hence, it’s necessary to find better local minima because better local minima tend to lead to higher prediction accuracy. In [12], a global continuation technique is presented. In [21], a similar global smoothing homotopy method is given. However, both the method is experiential and the calculations are lengthy.
The focus of this paper is giving a new efficient implementation of the smoothing homotopy method for the S3VMs. In Section 2, we first introduce the new S3VMs model used in [21] and list two smoothing functions called aggregate function and twice aggregate function respectively. The two smoothing functions are given to approximate the nonsmooth objective function (the detailed discussion of these two smoothing functions can be seen from [4]). And then the smoothing homtopy method solving S3VMs is recalled. In Section 3, the new truncated smoothing technique is established to give a more efficient pathfollowing implementation of the smoothing homotopy method. The new technique is based on a fact that, some “non-active” data do little effect on the value of the smooth approximation functions with their gradients and Hessian during the computation, as a result, these “non-active” data can be filtered by the new truncated technique to save the computation cost. With the inexact computation technique, only a part of original data is necessary during the computation of every iteration. In the last section, Two artificial data sets with six standard test data from [10] are given to show the efficiency of our method.
A word about the notations in this paper. All vectors will be column vectors unless transposed to a row vector by a prime superscript T. The scalar (inner) product of two vectors x and y in the n-dimensional real space 
will be denoted by
. For a matrix
, 
will denote the 
th row of
. For a real number
, 
denotes its absolute value. For a vector
,
denotes its 1-norm, i.e., 
, 
denotes its infty-norm, i.e.,
. For an index set
, 
denotes the element number of it. For a given function
, if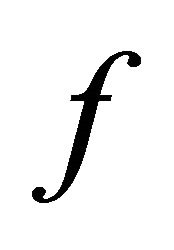 
is smooth, its gradient is denoted by
, if 
is nondifferential, denote its subdifferential as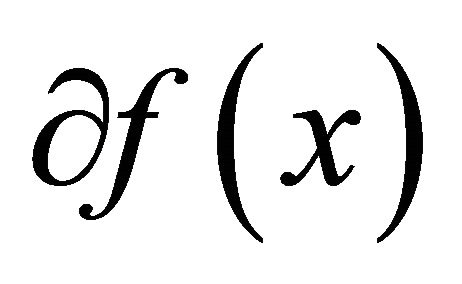
.
2. Semi-Supervised Support Vector Machines
There lies several formulations for S3VMs such as the mixed integer programming model by K.P. Bennett et al. [7], the nonsmooth constrained optimization model by O.L. Mangasarian [5], and the smooth nonconvex programming formulation by O. Chapelle [13] and etc. Here we mention the contributions by O. Chapelle et al. in [11-14]).
Given a dataset consisting of m labeled points and p unlabeled points all in
, where the 
labeled points are represented by the matrix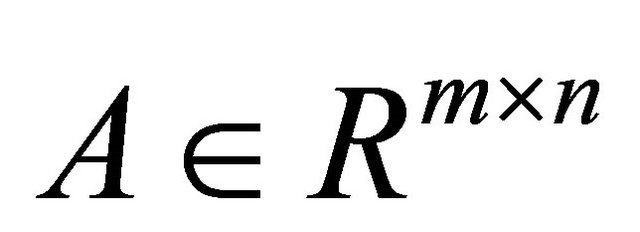
, p unlabeled points are represented by the matrix 
and the labels for 
are given by 
diagonal matrix 
of
. The linear S3VMs to find a hyperplane 
far away from both the labelled and unlabeled points can be formulated as follows:
(1)
where
and 
are loss functions corresponding to the labeled data and unlabeled data respectively and defined as follows,
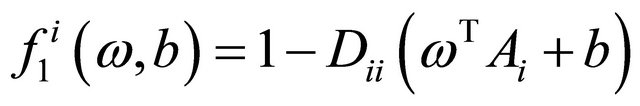
where 
denotes the absolute value of
. The constraint is called balanced constraint that is used to avoid unbalanced solutions which classify all the unlabeled points in the same class.
For arbitrary vector
, there lies an equivalent relation between its 1-norm and inf-norm in the sense that
, then the sum term of model (1)
can be substituted by the inf-norm form and model (1) can be reformulated as follows,
(2)
where
.
We rewrite the constraint into the objective as a barrier term and reformulate 
into its equivalent formulation
, and then obtain the following formulation that is our goal in the paper.
(3)
where
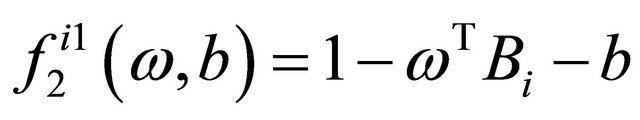
is a barrier parameter.
If the dataset is nonlinear separable, we need construct a surface separation based on some kernel trick (detailed discussion of it can be seen from [2] and etc.). Denote
, assume that the surface we want to find is
, where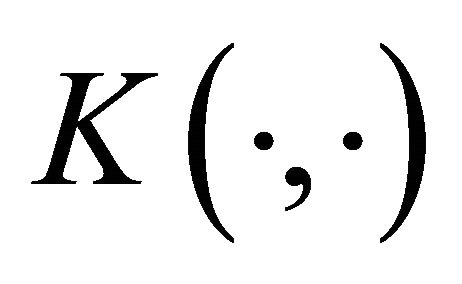 
is usually taken as Gaussian kernel function with the form of
is the kernel parameter,
. To find the nonlinear decision surface, we need to solve the following problem:
(4)
where
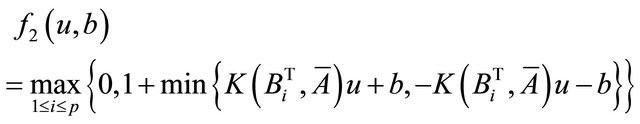
2.1. Aggregate Function and Aggregate Homotopy Method
Aggregate function is an attractive smooth approximate function. It has been used extensively for the the nonsmooth min-max problem [4], variational inequalities [6], mathematical programm with equilibrium constraints (MPEC) [16], non-smooth min-max-min problem [6] and etc. In the following, we will utilize the approximate function with its modification to establish an globally convergent method, called as aggregate homotopy method, for solving model (3) or (4).
In short, let 
(or,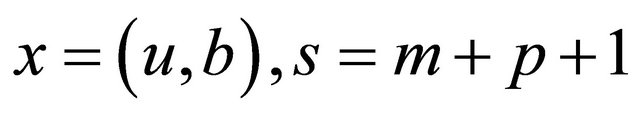
) and denote model (3) or (4) as the following unified formulation:
(5)
where
(6)
and 
are defined as (3) or (4).
Denote
, based on the optimality condition of non-smooth optimization theory in [9], we know that the subdifferential of 
and 
can be computed as follows,
(7)
where
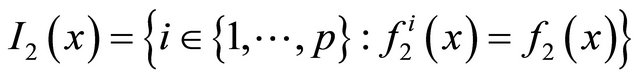
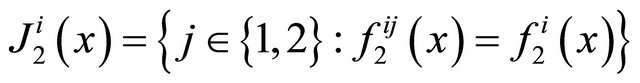
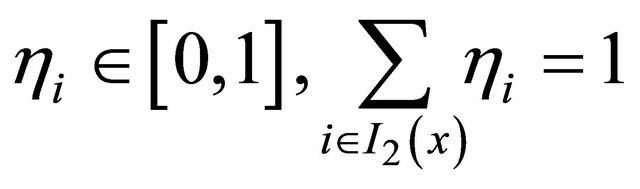
moreover, a point 
can be called a stationary point or a solution point of (5) if satisfying
.
To solve model (5) by an aggregate homotopy method, we first introduce the following two smoothing functions,
(8)
where 
is defined as (6) and
.
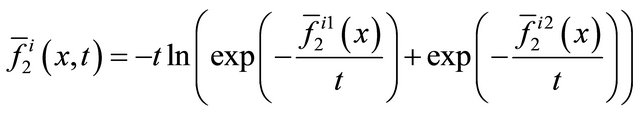We call 
and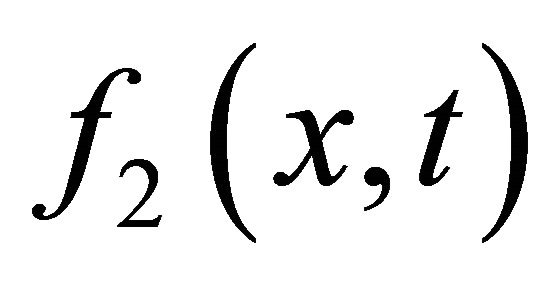 
as aggregate function and twice aggregate function respectively. The two smoothing functions have many good properties such as uniform approximation and etc. More details can be seen from [19].
Using above two uniformly approximations functions in (8), we define the following homotopy mapping:
(9)
where 
is an arbitrarily initial point and
.
We call Equation (9) as an aggregate homotopy equation. It contains two limiting problems. On the one hand as
, it has a unique solution
. On the other hand, as
, the solution of it approaches to a stationary point of (5), i.e., a solution 
satisfying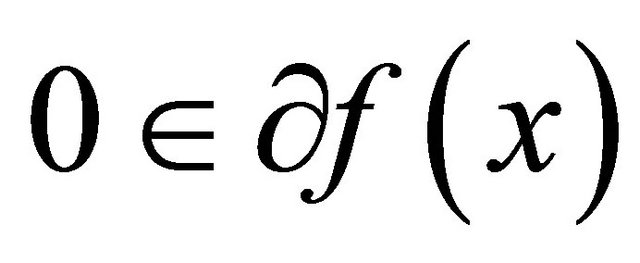
.
For a given initial point
, we denote the zeros point set of the aggregate homotopy mapping 
as
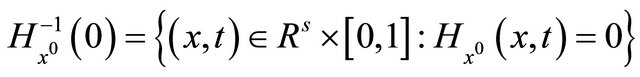(10)
It can be proved that 
includes a smooth path 
with no bifurcation points, starting from 
and approaching to the hyperplane 
that leads to a solution of the original problem [21].
3. Inexact Predictor-Corrector Implementation of the Aggregate Homotopy Method
The path-following of the homotopy path 
can be implemented by some predictor-corrector procedure. Some detailed discussion on the predictor-corrector algorithm with the convergence can be seen from [3,8] and etc. In the following, we first give the framework of the predictor-corrector procedure in this paper, and then discuss how to make an inexact predictor-corrector implementation.
3.1. Predictor-Corrector Path-Following Algorithm
Parameters. initial stepsize
, maximum stepsize
, minimum stepsize
, stop criteria 
for procedure terminated, stop criteria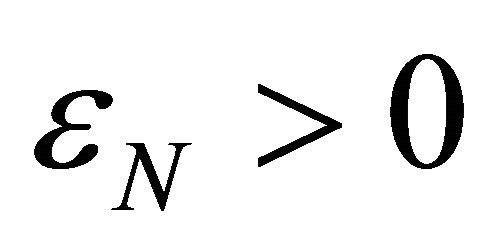 
for Newton corrector stopped, criteria 
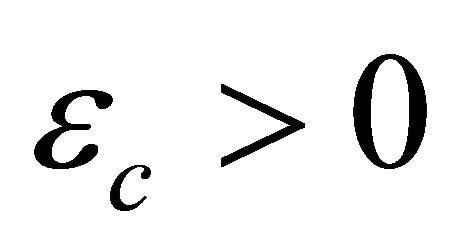for judging corrector plane, counter
.
Data.
Step 0.
, 
,
.
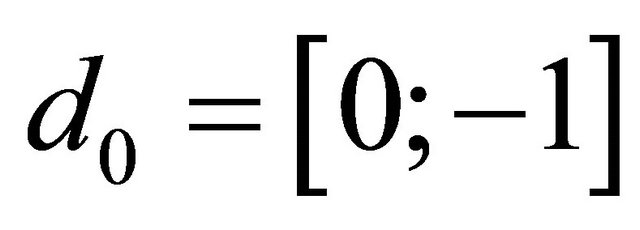Step 1. Compute a predictor point 
1) Solve the following linear equation
to obtain a unit tangent vector
;
2)
;
;
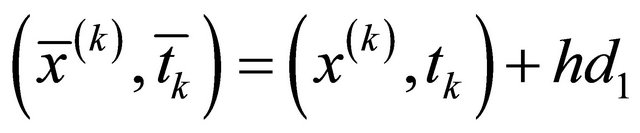3) If 
or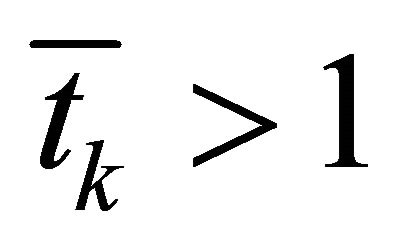
, 
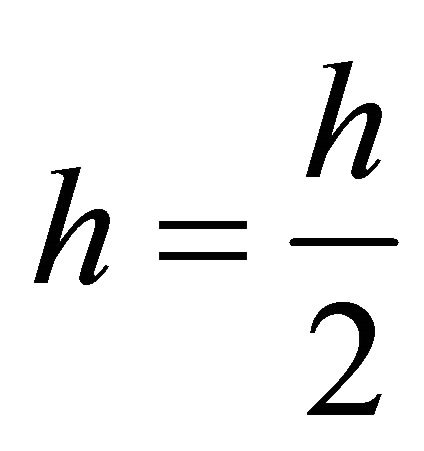, return to 2); else, go to Step 2;
Step 2. Compute a corrector point 
1) If
, take 
and
; else, take
. Go to 2);
2) Solve equation
by Newton method with the stopping criteria 
and go to 3);
3) If Newton corrector fail, 
, go to 2); else, denote the solution as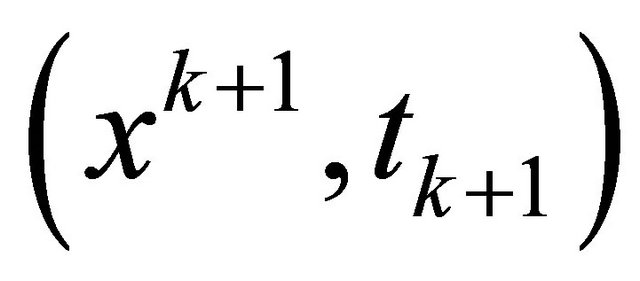
, go to 4);
4) If 
or
, 
, go to 2); else, go to 5);
5) If
, stop ; else
, k = k + 1, go to 6);
6)
. If 
and the iteration number of Newton corrector is less than 3, go to 7); else , go to 1);
7)
,
; go to 1).
Notice that, the main computation cost of Algorithm 3.1 lies in the equations solver in Step 1) and 2), some inexact computation technique can be introduce to save the computation cost of them. we take the following approximate homotopy equation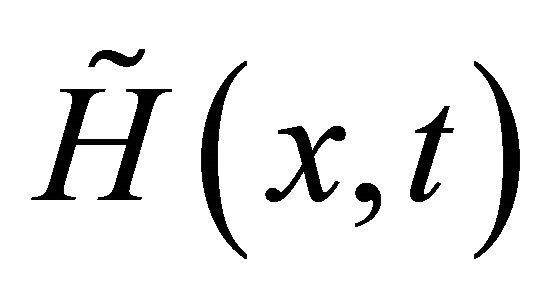 
with its Jacobian 
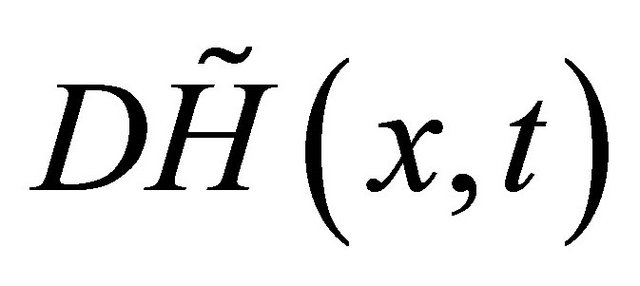in place of the original 
with 
during the computation of step 1) and 2).
Given parameters
, 
, denote
, 
,
where
It’s proven in [20] that, only if the error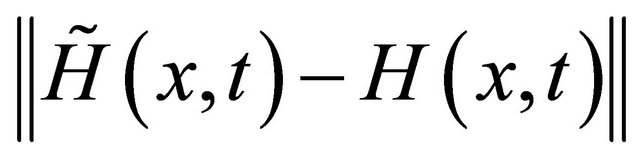 
and 
are small enough, or equivalently,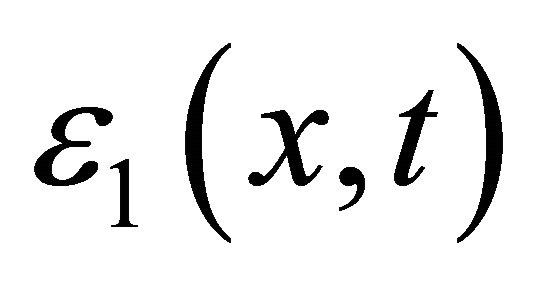 
and 
are chosen appropriately, the approximate Euler-Newton predictor-corrector also approaches to a solution of original problem. Here we only list the main results and omit the proofs.
Denote
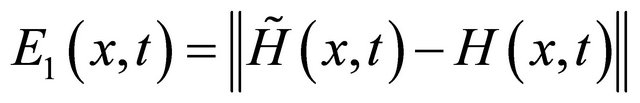
and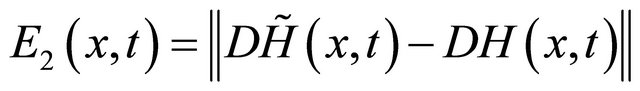
, 
is the unit tangent vector obtained by the approximate computation, 
is the tangent vector by exact Euler predictor, we have the following lemma to guarantee the efficiency of the approximate tangent vector.
3.2. Lemma
For a given
, if 
is small enough and satisfies
The approximate unit predictor tangent vector 
is effective, i.e., 
still makes a direction with arclength increased.
During the correction process, the following equation must be solved
(11)
where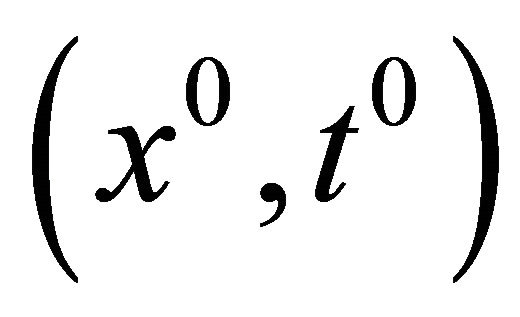 
is an appropriate predictor point obtained from the former predictor step. We adopt the following approximate Newton method to solve (11),
(12)
where
From 0 is a regular value of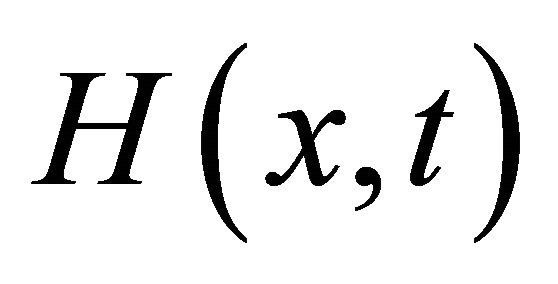 
and 
is a unit tangent vector induced by
, we know, if the step 
is chosen appropriately, the equation (11) has a solution and the approximate Newton iteration (12) is effective.
3.3. Approximate Newton Corrector Convergence Theorem
Suppose that 
have solution 
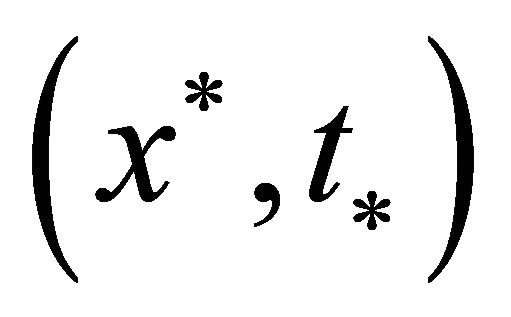with nonsingular
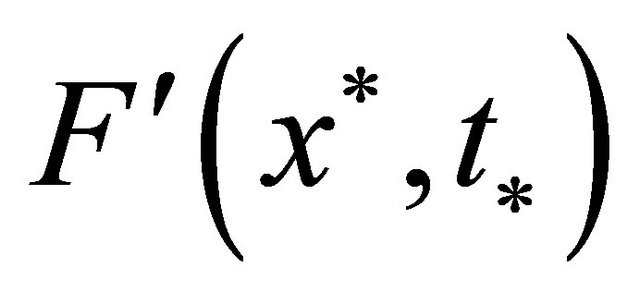, there exists a neighborhood 
and
, for any
, if for each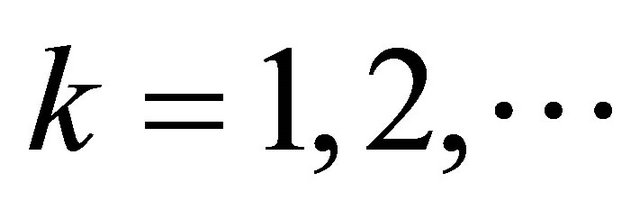
, 
and 
satisfying
.
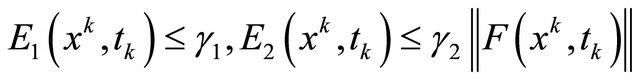Then the approximate Newton iteration point sequence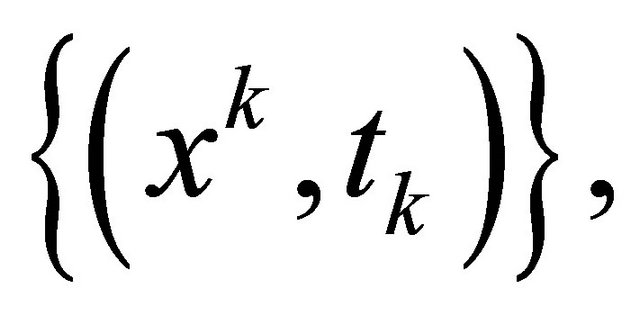 
from (12) is well defined and converges to
.
4. Numerical Results
In this section, some numerical examples and comparisons are given to illustrate the efficiency of our method. Two artificial datasets are generated first. The first one consists of 34 points generated by “rand” function, 14 of them are labeled and the remaining 30 are seen as unlabeled data. The second one consists of 242 points taken from two nonlinear bihelix curves that are generated by
, where one is obtained by taking
, the other is by taking
,
. We take randomly 
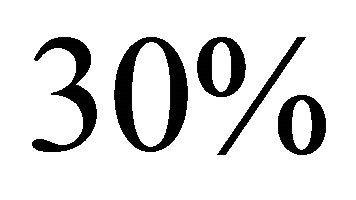of them as labeled and the remaining 
as unlabeled. The comparisons of our method with the LSVM method from [15] without the consideration of unlabeled data are given. Final results are illustrated in Figures 1 and 2.
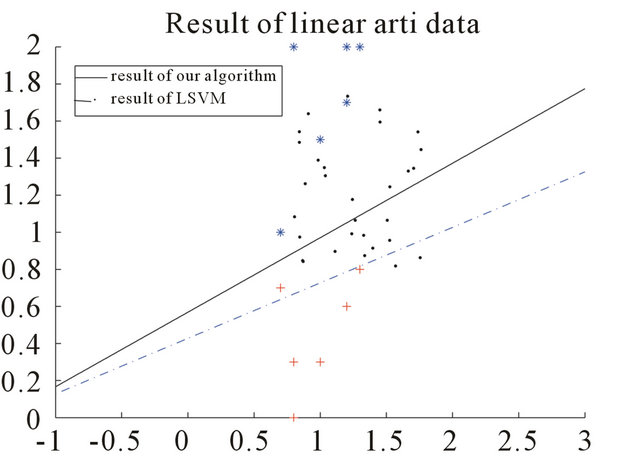
Figure 1. Result on linear artificial data of LSVM and the new algorithm.
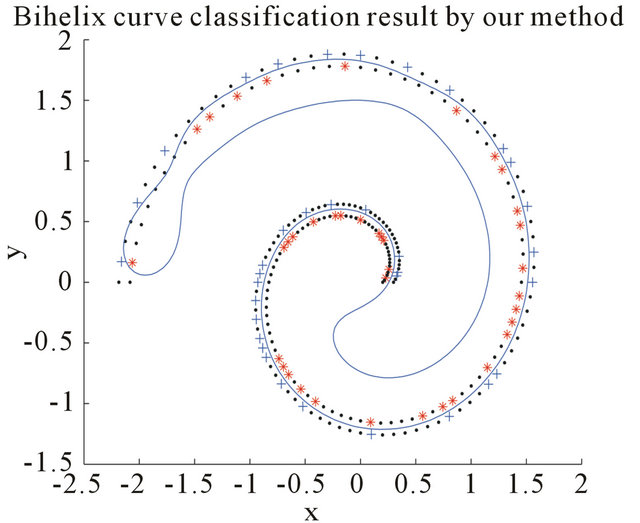
Figure 2. Result on nonlinear bihelix curve artificial data of LSVM and the new algorithm.
To reveal the efficiency of our algorithm for S3VMs, comparisons of our algorithm (InSH) with some other existing algorithms for S3VMs such as the convexconcave procedure in [5] (vS3VM), the continuation method in [12] (cS3VM) and the gradient descent method in [13] (
S3VM), are given for some standard test data from [10]. For the linear programming subproblem arising in [5], we solve it with the Matlab function 
in optimization toolbox. The comparison results are listed in the following Table 1.
Table 1. Comparison Results on test data (test error %).
-: denotes the method fails for the dataset.
All the computations are performed on a computer running the software Matlab 7.0 on Microsoft Windows Vista with Intel(R) Core(TM)2 Duo CPU 1.83 GHz processor and 1789 megabytes of memory. During the computation, we take
, 
, 
, 
, 
, 
, 
, 
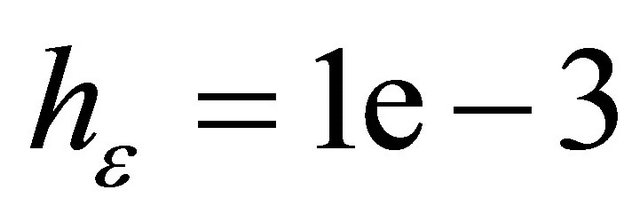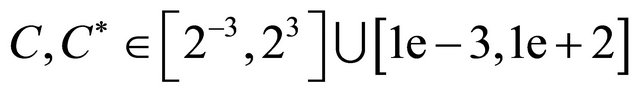are taken as the one for the least test error. If necessary, the kernel parameter 
is taken the best leads to the least test error among
. The parameters for determining the inexact index set are taken as
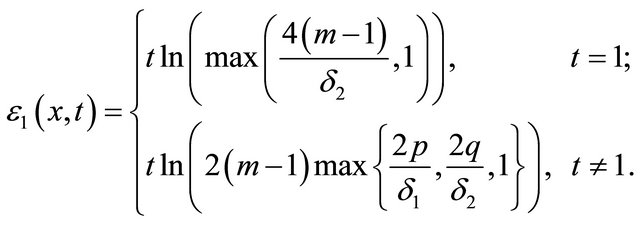
where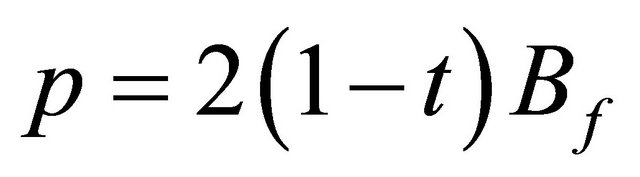
, 
, 
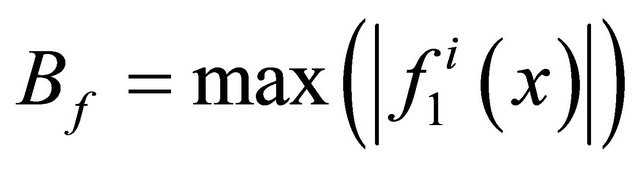and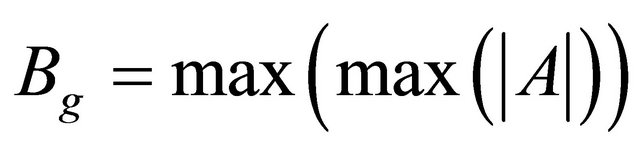
. 
has the same expression as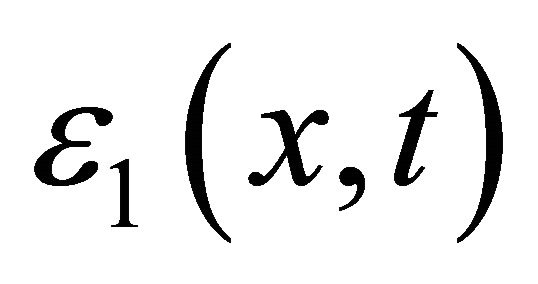 
where 
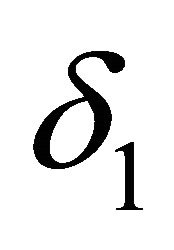and
. 
and 
are taken as 
that are given to bound the error of 
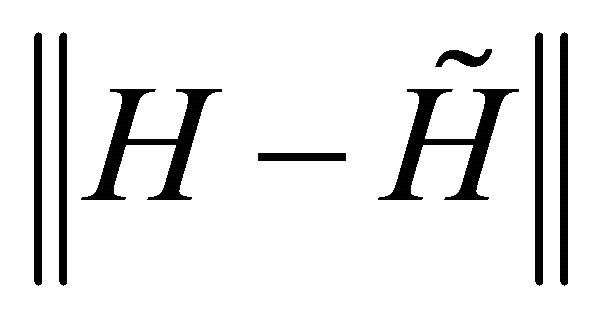and
.
5. Acknowledgements
The research was supported by the National Nature Science Foundation of China (No. 11001092) and the TianYuan Special Funds of the National Natural Science Foundation of China (Grant No. 11226304).