Extraction of the Speed of Gravity (Light) from Gravity Observations Only ()
1. Introduction
In 1890, Maurice Lévy [1] suggested that the speed of gravity is equal to the speed of light. Poincaré [2] argued in 1904 that the speed of gravity could not be larger than the speed of light in vacuum. The speed of gravity in Einstein’s general relativity theory [3] is assumed to be the same as the speed of light [4] [5] . Still, there exist a series of alternative gravity theories assuming that the speed of gravity is much greater than the speed of light, see, for example, [6] [7] [8] [9] for such models and discussion on them. To measure the speed of gravity is therefore of great importance to find out which theories can be ruled out and which ones are worth exploring further [10] [11] .
There have been several indirect detections of the speed of gravity in the past. For example, [12] , based on information from a rather complex set-up including quasar observations, concluded that the speed of gravity
was between 0.8 and 1.2 times the speed of light in vacuum. In more recent times, advanced experimental studies in relation to gravity waves claim to support the idea that the speed of gravity is in the ball park of the speed of light in a vacuum [13] [14] [15] . Clearly, these measurements give a very wide confidence interval for the speed of gravity, something to which we return later in this paper. These experiments are based on very complex set-ups and also, we would say, a complex set of assumptions.
This paper will show how we can extract the speed of gravity (light) from a series of simple gravity observations. The approach explained is much simpler conceptually and experimentally than gravity wave experiments. Our theory also supports the concept that gravity is moving at the speed of light, and the experiments suggested will likely give a very narrow confidence interval for the speed of gravity. It can be questioned if we are finding the speed of light or the speed of gravity in our method. Alternatively, they could perhaps be the same, if electromagnetism and gravity at a deeper level are connected, as they could be in a yet-to-be discovered unified theory. This will be discussed briefly in Section 6 of this paper.
2. Extracting the Speed of Gravity (Light)―The Simple Way
The speed of light is an input factor in several gravity formulas, such as the calculation for the Schwarzschild radius
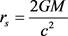 (1)
(1)
1We will claim that the Newton method, as typically used, is not that sound because it involves a kinetic energy formula of the form
in the derivation. This formula is clearly only valid when
.
The formula can also be found from Newton’s gravity theory [16] by setting the radius equal to the point where Newton’s escape velocity is the speed of light1. In addition, it can be derived from Einstein’s theory of general relativity [3] in combination with the Schwarzschild metric [17] [18] because the escape velocity there supposedly is the same [19] . In 1784, Michell first calculated what radius would give an escape velocity equal to the speed of light, see [20] . He also hypothesized that the star would be dark. General relativity has a different interpretation and a much wider theory on these objects, which are seen as black holes in that context. We will not discuss black holes versus dark stars and the possibilities of such objects, but it is important to keep in mind that when we talk about the Schwarzschild radius here, it is also linked to Newton’s gravity theory, since the same radius can be calculated from that theory.
Further, the Schwarzschild radius is related to gravitational time dilation (gravitational time dilation was first suggested by Einstein)
 (2)
(2)
where
is the time as measured at a radius of
,
is the time measured at a radius of
from the center of the gravitational object
, and
and
are the escape velocities at the two different altitudes. In other words, the speed of light is input from several gravitational phenomena that have been confirmed by observations. However, to our knowledge little has been written about working the calculation the other way around, namely using gravitational observations to measure the speed of light. This is also interesting from a fundamental point of view. Why can we find the speed of light, as we will show, simply by observing gravitational phenomena? In undertaking this exploration, we will gain some insight into how the gravity formulas were derived in the first place.
2.1. Speed of Gravity/Light from a Gravitational Red-Shift Experiment
If we shoot a laser beam of light from the top of a tower to the bottom of the tower, we can measure the redshift, with respective radii of
and
to the center of the Earth. The gravitational redshift is then given by
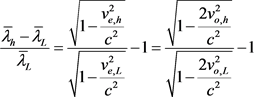 (3)
(3)
where
and
are the escape velocity and the orbital velocity at these two radii, and
and
are the wavelengths at the two altitudes. Solved with respect to c, this gives
 (4)
(4)
In a weak gravitational field,
and this can be well-approximated as
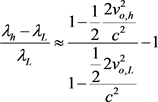 (5)
(5)
Solved with respect to c, this gives
 (6)
(6)
And since , we can also find the speed of the light from measuring the
, we can also find the speed of the light from measuring the
gravitational acceleration at the two altitudes instead of using the orbital velocities; this gives
 (7)
(7)
We can also do the weak field approximation
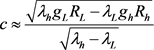 (8)
(8)
If the redshift is measured from two altitudes on Earth, then the gravitational acceleration field is naturally preferable. But we could also send a laser beam between two satellites orbiting the Earth at different altitudes and then we could just as well use the orbital velocities.
2.2. Speed of Gravity from Orbital Velocity and Two Atomic Clocks
If we have two atomic clocks sitting at different altitudes, then we have
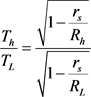 (9)
(9)
 (10)
(10)
Solved with respect to the speed of light, we get
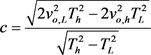 (11)
(11)
Obviously the Earth is rotating, so if the work is not done at the poles then we must take the different rotational speeds of the Earth at different altitudes into account (see [21] for an introduction on the topic). Therefore, we have
 (12)
(12)
Solved with respect to the speed of light, we have
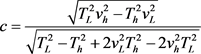 (13)
(13)
Table 1 below summarizes ways to extract the speed of light (gravity) from gravitational observations alone.
Figure 1 illustrates some of the ways we can find the speed of gravity (or just light) by only doing gravity observations. In Figure 1(a), we have two orbiting satellites, we send light between them and measure the redshift. In addition, we measure the orbital velocity of the satellites and from this we know the speed of light. In Figure 1(b), we measure the gravitational time dilation at two altitudes, as well as the Earth’s gravitational acceleration field at each altitude, and from
![]()
Table 1. Ways to measure (extract) the speed of light/gravity from gravitational observations.
![]()
Figure 1. Illustrations of two set-ups where we can measure the speed of light only from gravity observations. In the figure, we also see what observations need to be done at each location.
this we know the speed of light (gravity).
3. No Need to Know G or the Mass Size or Even the Speed of Light to Find the Schwarzschild Radius and to Predict Other Gravity Phenomena
The past scientific literature does not seem to mention the fact that one can easily find the Schwarzschild radius (for example of the Earth) without any prior knowledge of the Newton gravitational constant or any knowledge of the mass size. This can be done by using the following relation
(14)
where
is the gravitational acceleration that on Earth’s surface can be observed with no knowledge of gravitational theory. Further, the speed of light and the radius of the Earth can be found without any knowledge of gravitational theory. We have found that a long series of gravitational phenomena can be predicted when one first has found the Schwarzschild radius without knowledge of G or the mass size, as clearly shown by [22] [23] .
Interestingly, we can even find (measure) the Schwarzschild radius by replacing the speed of light with our extracted speed of light, as shown in the sections above. The Schwarzschild radius can be found based on the following formula
(15)
where
and
are the wavelengths of a light beam moving out from or towards Earth, as measured from radius
and
respectively (where
). In other words, it is directly linked to the gravitational redshift of light. For example, one can measure the wavelength of a light beam at the top of a tower (tall building) and the bottom of a tower (see Pound and Rebka Jr. [24]). This is all that is needed to know the Schwarzschild radius of the Earth. The important point is that we can extract the Schwarzschild radius without the Newton gravitational constant and with no knowledge of the speed of light (gravity) or the mass size. All we need to know is the gravitational redshift at two points. Thus we may question if the Schwarzschild radius really is a radius related to black holes, or if it represents something more profound and linked to all (or most) gravity phenomena.
Table 2 shows how a series of major gravity phenomena can be predicted simply from two observations of a light beam plus a measurement of the speed of light. This is done by measuring the wavelength of two distant points and knowing the radii where the measurements are taken relative to the gravity object (for example the Earth). This seems to provide a clear proof that gravity is directly linked to light and therefore, the speed of gravity must be exactly the speed of light.
General relativity theory has not been able to link its theory to quantum physics;
![]()
Table 2. The table shows that all major gravity phenomena can be predicted by only two (or three) observations from a light beam in the gravitational field of the gravity object. We need to measure the wavelength at two altitudes of a light beam plus the speed of light. There is no need to know the Newton gravitational constant or the mass of the gravity object. This also strongly supports the ideas that there is a direct connection between electromagnetism and gravity and that the speed of gravity is actually the speed of light. The radius R is where we want to perform the gravity prediction, and
and
are the radii where we perform the wavelength (or frequency) observations.
in spite of many efforts in the physics world, a unified theory is still missing. We think the Schwarzschild radius plays an important role in gravity, but that it is related to some quite different aspects of matter than those assumed by standard theory. The Schwarzschild radius is, in our view, the reduced Compton frequency per Planck
second multiplied by the Planck length, that is
, be
aware that both
and
can be measured independent of GR and without any knowledge of big G, see [25] [26] . For any known elementary particle, such as the electron, the reduced Compton wavelength is much larger than the Planck length. We will suggest that this means the Schwarzschild radius for particles with mass smaller than the Planck mass should be interpreted as a probabilistic Schwarzschild radius. In our view, all elementary particles have a Schwarzschild radius equal to the Planck length, but this comes in and out of existence at the Compton frequency of the particle. This means the Schwarzschild radius of an elementary particle smaller than the Planck mass simply is the Planck length
multiplied by a probability that is given by:
. So, the Schwarzschild radius is twice the Planck length multiplied by this probability.
When
is smaller than the Planck length, something we claim only can happen for a composite mass, then we will have
; the integer part of this
number means certainty, that is the number of whole Planck length, while the remaining fraction should be viewed as a probability. Here the Schwarzschild radius holds from the smallest elementary particle, such as an electron, to the largest mass. Particles with a Schwarzschild radius smaller than the Planck length simply means the Schwarzschild radius comes in and out of existence. We do not think there exists an physical Compton wavelength shorter than the Planck length, but the Compton wavelength from different particles can be
added, based on the following rule,
, something
that means any mass has a Compton wavelength, even if a composite particle does not have one physical Compton wavelength, but many. Still, the Compton wavelength of the composite mass will lead to the correct Compton frequency. Further, recent research seems to directly link matter to Compton time, see [27] [28] .
In our view, the Schwarzschild radius itself can never be smaller than the Planck length; a smaller radius, as is the case for any observed elementary particle, does not mean such particles do not have a Schwarzschild radius, it means their Schwarzschild radius comes in and out of existence and that gravity is probabilistic below the Planck mass scale. That is to say, probability should be dominant in gravity for masses much smaller than the Planck mass, which would hold for all observed elementary particles.
4. When Using Gravity Observations (Only) Are We Measuring the Speed of Light or the Speed of Gravity?
We have shown a series of ways to extract the speed of gravity from observations normally only linked to gravity. But is it “just” the speed of light we can extract in this way? If we claim it is the speed of light we are extracting and not the speed of gravity, then why should the speed of light be hidden in a series of gravity phenomena such as time dilation and gravitational acceleration fields, as well as gravitational redshift? Doesn’t this indicate that electromagnetism is linked to gravity? Or we could claim it is only the speed of gravity we have extracted, as it is only from gravity phenomena. It does appear that the speed of light and the speed of gravity are one and the same thing, and align with the case where, at a deeper level, we expect to find a unification of electromagnetism and gravity; this is obviously an old, but ongoing debate [29] - [35] . We would strongly suggest that such unification of electromagnetism and gravity is also observable at the macroscopic scale, not only at the quantum scale. There are many opinions here and we will not draw conclusions prematurely, but encourage more physicists to study this, both theoretically and experimentally.
It is well known that the Coulomb electrostatic force [36] and the Newton gravity force theoretically are the same for Planck mass particles,
, where
and
are the Planck charge and
the Planck mass, see also [37] . Is it not a bit strange that the speed of light suddenly shows up in Newton’s gravity theory when working at the Planck scale and otherwise it is assumed by many physicists that Newtonian gravity is instantaneous? We know the speed of light is linked to the Coulomb electrostatic force as
. Recently, it has also been suggested that the speed of light is embedded in Newton’s gravitational constant. Haug has [38] [39] [40] suggested
that Newton’s gravitational constant is a composite constant
. McCulloch [41] [42] has suggested
, which basically is identical to our composite
gravity constant, but he has pointed out that this leads to a circular problem, as he has followed the common assumptions in modern physics on this point, e.g., that one needs to know G to know
and that his composite G then cannot be known without G. We, on the other hand, have shown that the Planck length can be found with no knowledge of G, see [25] [26] [43] . Then all the parts of this composite constant can be found independent of existing gravity theories. If this view is correct, then the speed of light, which likely is the same as the speed of gravity, is embedded in almost all gravity phenomena and it is not surprising that we can extract the speed of gravity from a series of gravity phenomena, without detecting gravity waves, and in a much simpler way. The Planck length is something we logically can relate to―it is a minimum length. The speed of light is how fast the fastest particle (photons) can move, and it is the longest distance something can travel in any given time interval. The gravitational constant, on the other hand, does not seem to correspond to anything logically or physically, as its dimensions are m3∙kg−1∙s−2. Newton’s gravitational constant is clearly a universal constant, but in our view, it is a composite constant that consists of more fundamental constants. In particular, we think the Planck length and the speed of light (gravity) are essential for all gravity phenomena, even at the cosmological scale.
We are in no way indicating that Newton had any idea that gravity moved at the speed of light; the speed of gravity is often assumed to be infinite in Newtonian theory. But the speed of gravity in that theory is not truly reflected in the formula. It is indeed the lack of any speed in Newton’s gravity formula and Newton’s speculations that gravity was infinite that led many others to think it
must be infinite. Newton’s gravity formula is simply
. To get it to fit
experiments, the formula had to be calibrated, that is, one had to introduce an unknown parameter, today know as big G (or simply the Newton gravity constant). The gravity constant is today experimentally found from what we can call gravitational model calibration. What exactly the gravity constant represents is diffuse, at best. If the speed of gravity plays a central role in all gravity phenomena, then it must be embedded in the Newton formula, even if it simply is as part of a composite constant calibrated to observations. If not, Newton would not have been able to predict the simplest gravity phenomena accurately. The fact that Newton theory does not predict the perihelion of Mercury correctly could simply be due to relativistic effects that not have been taken into account properly, see [44] for a recent discussion on this.
In 1798, the gravity constant was first measured indirectly when Cavendish wanted to weight the Earth with a torsion balance. And it was likely first in 1873 that the Newton gravity constant was mentioned explicitly by Cornu and Baille [45] . Again, it is still a mystery what the gravity constant truly represents. However, returning to recent measurements of the speed of gravity, based on the recent gravitational wave detection Cornish, Blas, and Nardini [14] claim
“using a Bayesian approach that combines the first three gravitational wave detections reported by the LIGO Scientific and Virgo Collaborations we constrain the gravitational waves propagation speed
to the 90% credible interval
, where c is the speed of light in vacuum.”
we are not questioning their measurements or predictions here, but it also interesting if we can measure the speed of gravity in a much simpler way using the methodology suggested in this paper.
5. Isotropic or Anisotropic?
It has been suggested that the speed of gravity could be anisotropic [46] . It is therefore of interest to know if our extraction of the speed of gravity (light) from the experiments suggested in this paper could be helpful in this respect. To discuss this, we will address an old and ongoing debate related to the question of whether the one-way speed of light is isotropic or anisotropic. The idea that the one-way speed of light is constant and the same in every direction, e.g., isotropic, was likely first introduced by Poincaré. In the year of 1898, Poincaré [47] published a philosophical paper titled: The Measure of Time. In this article, Poincaré points to how astronomers often assume the speed of light is constant and the same in every direction:
When a astronomer tells me that a stellar phenomenon, which his telescope reveals to him at this moment, happened, nevertheless, fifty years ago, I seek his meaning, and to that end I shall ask him first how he knows it, that is, how he had measured the velocity of light. He has begun by supposing that light has a constant velocity, and in particular that its velocity is the same in all directions. That is a postulate without which no measurement of this velocity could be attempted. This postulate could never be verified by direct experiment.
Poincaré here indicates that it would be impossible to detect the true one-way speed of light in any type of experiment. The problem with this method is that to measure the one-way speed of light, we need to synchronize two clocks, and to synchronize two clocks we need to know the one-way speed of light. We end up with a circular problem. This is likely the reason Poincaré assumed that we could never measure the one-way speed of light and thereby assumed that the one-way speed of light was isotropic for synchronization purposes. In 1905, Einstein [48] goes one step further and simply abandons the ether and by this he also assumes that the one-way speed of light is isotropic. It can also be shown that slow clock transportation synchronization basically corresponds to Einsten-Poincaré synchronization, so this synchronization procedure cannot, in general, be used to set up experiments to detect the one-way speed of light, see [49] [50] .
However, it is worth mentioning that a series of experiments have attempted to circumvent the Einstein-Poincaré synchronization procedure in order to detect whether the one-way speed of light is isotropic or anisotropic. A series of experiments have claimed to have detected anisotropic one-way speed of light, see [51] - [57] , but many of these experiments have also been criticized, see, for example, [58] [59] . The debate around the one-way speed of light continues to this day [60] [61] [62] [63] and it also remains an open question whether the one-way speed of gravity is isotropic or anisotropic as well.
When it comes to our extraction of the speed of gravity (light) from gravity observations, these often involve two very precise clocks, atomic or optical clocks placed a distance apart. These clocks need to be synchronized, which intuitively suggest that our methods cannot be used to detect if the speed of gravity (light) is isotropic or anisotropic. On the other hand, in experiments where we only need to detect the redshift, then no clock synchronization should be necessary and this could possibly be used to measure the one-way speed of light (gravity). The main challenge would be to attain the degree of accuracy required, as we would also need to measure the gravitational acceleration at each altitude.
If it is the speed of gravity we actually are extracting and not only the speed of light, then the approaches in this paper are still very interesting. This means one does not need to rely on very sophisticated theories, such as gravity waves detectors, to detect the speed of gravity, but instead we can use much simpler experiments. However, if this is not giving us the speed of gravity, then we need good arguments to address why the speed of light is hidden in so many gravitational phenomena and how we can predict all major gravity phenomena, such as orbital velocity, gravitational time dilation, gravitational acceleration, and the Schwarzschild radius, all without any knowledge of G, c, or the gravity mass, but simply from a beam of light in the gravity field.
6. Conclusions
We have shown how one can, in a simple way, extract the speed of light (gravity) from gravitational observations alone. Even if it only seems to consist of a rearrangement of existing formulas, the exercise and analysis can lead to new insights. We would note some things are so simple that they seem obvious when first pointed out, but they may have deeper implications and certainly deserve further examination.
It is, at present, an open question on whether or not there is a link between gravity and electromagnetism, and there is a renewed interest in the link between the two. We have shown how a series of major gravity phenomena can be predicted by some simple observations of a light beam, namely its velocity and its wavelength at two altitudes in a gravitational field. This may provide a small breakthrough in the current insights around gravity. A unified theory between electromagnetism and gravity is still missing, but hopefully this takes us one step further in the right direction.
Acknowledgements
Thanks to Victoria Terces for helping me edit this manuscript and thanks to an anonymous referee for useful comments.
Appendix
In this appendix, we show the cases where we want to measure/predict the gravitational phenomena at one of the same radii from which we measured the wavelength of the beam; see Table 3.
![]()
Table 3. The table shows that all major gravity phenomena can be predicted by only two (or three) observations from a light beam in the gravitational field of the gravity object. We need to measure the wavelength at two altitudes of a light beam plus the speed of light. There is no need to know the Newton gravitational constant or the mass of the gravity object. This also strongly supports the ideas that there is a direct connection between electromagnetism and gravity and that the speed of gravity is actually the speed of light.