Mapping the Wall-Region Dynamics of High-Flux Gas-Solid Riser Using Scaling Regions from the Solid Concentration Time Series ()
1. Introduction
The application of chaos analysis in studying non-linear systems is one of the best techniques that provide significant understanding of the chaotic dynamic systems [1]. Such systems include the gas-solid circulating fluidised bed risers which are extensively used in various industrial applications including the gas-catalytic reactions systems like the fossil fuel production industries [2] [3]. However, the productivity of these processes depends largely on the dynamics of the gas-solid suspension flow behaviours in the reactor systems [2] [4]. Thus proper understanding of the gas-solid flow behaviours is vital to the successful operations since the hydrodynamics in such systems influences the mass transfer, heat transfer, the gas-solid interactions, reaction rate and yield [1] [2] [3].
The gas-solid flow in the fluidized bed systems has been shown to be complex and governed by the non-linear relationships. In particular, studies show that solid concentration time series signals from the circulating fluidised bed riser exhibit non-linear relationships that are characterized by low dimensional deterministic chaos and therefore require non-linear techniques for proper analysis [1] [5] [6]. Thus, to accurately understand and describe the dynamics of such system it necessitates the use of non-linear techniques such as chaos analysis which are based on the construction of an attractor of the dynamic evolution of the system in state-space [1] [5].
Chaos analysis is one of the successful techniques in studying the dynamics of the gas-solid suspension flow in the circulating fluidised bed riser systems [1]. It involves determination of characteristic parameters that describes the reconstructed attractor such as correlation integrals and correlation dimensions. Correlation integral and correlation dimensions are the key parameters that are extensively used in studying the dynamic features of the chaotic system such as the circulating fluidized bed riser systems [1]. Correlation integrals are used in analysing and distinguishing the dependencies of dynamical variables and testing the randomness of chaotic time series data [7]. Further, several studies employed correlation integrals in estimating correlation dimension which are used to characterize complex and non-linear dynamical systems [8] [9] [10] [11].
Correlation dimension is a characteristic parameter that measures the fractal dimension of the time series which describes the complexity of the reconstructed chaotic attractor of the chaotic systems [9] [12]. It is one of the key parameters that give a quantitative description of the strangeness of the fractal attractor and also a means to identify chaotic processes [10]. Estimation of correlation dimension is accomplished from the slope of the linear part of the correlation sum function or correlation integral curves [10] [12]. The correlation integrals are computed from the data set and the correlation dimension is estimated from the linear section of the log(Cr) − log(r) or ln(Cr) − ln(r) plots, called the scaling region [9] [10]. However, the subject question for many researchers has been on the identification of the scaling region for the proper and accurate determination of the correlation dimension. In this study the correlation dimension was not determined but instead scaling regions were established in terms of location along the log(r) axis, due to changes in location and operating conditions.
Several studies have developed methods to identify the scaling region in order to accurately determine the correlation dimension. However, the commonly, easy and quickest method is reported to be the visual inspection method [10]. Though seems to be subject to the human decision, when used accurately may give significant and reliable dimension sufficient to describe and characterize the chaotic dynamical system. Since its inception by Grassbeger and Procaccia [8], the correlation dimension, D2, has been the mostly examined and employed dimension in describing the characteristic of the multifractal attractors of the chaotic dynamic systems [9] [10]. The dimension, D2, is mostly used in chaotic time-series processing and analysis since it is identified as one of the critical characteristic parameter for measuring chaotic properties of the non-linear time series. In such investigations, most of studies utilize the numerical system like the Lorentz system to examine the suitability of correlation dimension, D2, in explaining the underlying characteristics of the dynamic features of the chaotic system [10].
In this study we use real time series signals of the solid concentrations sampled from the high-flux CFB riser system to compute the correlation integrals and employ visual inspection method to identify and analyse the scaling regions. The study analyses the correlation integrals and scaling regions obtained as embedding dimensions increases in different radial positions of the wall region for different flow development sections of the riser at different operating conditions. Scaling regions obtained are analysed and compared. Formation of visible basin defined in this study as multifractal basin in some locations is also analysed and is the new observation and further extension from past studies. Further, the number of scaling regions for each curve of the correlation integral are examined.
2. Literature Review
2.1. Correlation Integral
The correlation integral or correlation sum, C(r), for a collection of points, xi, in some vector space is the fraction of all possible pairs of points which are closer than a given distance, r, in a particular norm; where r is the radius of the hypersphere. In this case the correlation sum or the correlation integral is referred to as the probability that a pair of points chosen randomly with respect to the natural measure is separated by a distance less than r on the attractor [9] [12]. The method of correlation integral or correlation sum consists of centering a hypersphere on a point in hyperspace or phase-space, by letting the radius of the hypersphere, r, increase until all points are covered in the realm of the radius. This happens when r equals or exceeds the maximum attractor’s size. The value of r is increased while keeping track of the number of data points that are enclosed by the hypersphere of that radius [13] [14] [15] [16] [17].
For a given m-dimensional phase space and the vector signals Xi and Xj, the correlation sum or correlation integral C(r) is given by [10] [11] [14] :
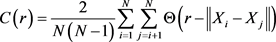 (1)
(1)
where
the vector distance (Euclidean distance) between two reconstructed vectors and
is the Heaviside step function, for which,
Substituting the vector distances
with the solid concentration signals,
, and express the equation using the Euclidean distance formula, Equation (1) becomes;
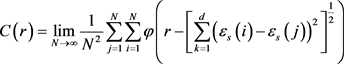 (2)
(2)
2.2. Scaling Region
Scaling region refer to the linear section of the correlation integral curve, i.e. the ln(Cr) − ln(r) curve. The scaling region can be defined as a domain with measurement invariability in which the object exhibit self-similarity over ranges of distance or trajectory scales [10]. It is from this linear portion of the curve where the correlation dimension is estimated. The correlation dimension estimator of the attractor is the slope of the scaling region of the correlation integral, C(r), versus hypersphere radius, r, as given in Equation (1) [1] [10]. Since the scaling region is used in computation of the correlation dimension which is used in characterization of the multi-fractal structure of the chaotic attractor [9], its identification is very crucial for an accurate determination of the correlation dimension. There are various methods established by various scholars to identify the scaling region. However, the simple and fast method identification method is by visual inspection though the method is reported to be subjective to the individual decisions which may lead to differences in estimation of the boundaries or the upper and lower limit of the straight section and therefore resulting in differences for the calculated correlation dimension [10].
Various studies show that in the limit of an infinite amount of data (
) and for small r, the correlation integral, C(r), scales like a power law [10] [14]. It is shown that, if the time series data set has an attractor, the relationship between the correlation integral, C(r), and the hyperspherical radius, r, is given by [10] [14] :
 (3)
(3)
Then, if the dynamical behaviour of the time series is periodic or quasi-periodic, the correlation dimension, D2 is equal to the topological dimension of the attractor, where for the chaotic dynamical systems it is a strange attractor and the computed fractal dimension, D2, is a non-integer number. The parameter D2 is the slope of the scaling region and Grassberger and Procaccia showed that it can be calculated from Equation (4) [9] [11] [14] :
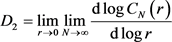 (4)
(4)
The slope D2 which gives an estimate of the correlation dimension is a characteristic quantity for time series and it shows how the correlation sum, Cr, scales with r. The slope of the linear section of the log(Cr) versus log(r) plot presents the important information required for characterization of the phase space attractor [18]. The slope of the log(Cr) versus log(r) plot can be estimated by the least square fit method of a straight line also termed as a scaling region over a certain range of hypespherical radius, r. The hyperspherical radius, r, is a radius interval of sufficient length for small r where the dimension D2 remains approximately constant and regarded as an estimate of the correlation dimension [19].
Studies show that for a given time series of finite length, N, the correlation sum depends on factors such as the delay time,
, and the embedding dimensions, m, [9]. This makes the correlation dimension to be calculated by observing the gradient of the scaling region, i.e. the straight section of the log(Cr) − log(r) curve by increasing the values of m [9]. When the embedding dimension, m < D2, then the dimension of the reconstructed phase space can not unfold itself enough to release all necessary information required to describe its characteristic behaviours. Therefore, the slope from the log(Cr) − log(r) curve gives an estimate or the range of the embedding dimensions as well. As the embedding dimension, m, increases, the attractor in the reconstructed phase space unfold itself improving its resolution. The slope of the linear section of the log(Cr) − log(r) plot increases as m increases until it saturates reaching a constant value which estimates the value of the correlation dimension, D2 of the attractor [9].
3. Methodology
3.1. Measurement of Solid Concentration Signals
Solid Concentration were collected from a CFB system shown in Figure 1 with a
![]()
Figure 1. The circulating fluidized bed with two riser system.
twin-riser having 76 and 203 mm internal diameters and 10 m high operated at 50 to 550 kg/m2s solids flux and 4.0 to 10.0 m/s gas velocity. Fluid catalytic cracking catalyst particles with 67 mm mean diameter and density of 1500 kg/m3 were used. A 70% to 80% humid air was used for transporting the solid particles. Signals were sampled from eight (8) axial levels (i.e. Z = 0.98, 1.52, 2.73, 3.96, 5.13, 6.34, 8.74, and 9.42 m) and 11 radial points (i.e. r/R = 0.00, 0.16, 0.38, 0.50, 0.59, 0.67, 0.74, 0.81, 0.87, 0.92, and 0.98) at each level where r/R is the normalized radial distances from the centre to the wall of the riser. To each point, 29,100 data points of solid concentration were sampled in 30 seconds using optical fiber probe at 970 Hz. In this study, a 76 mm riser was used and only 6 radial position in the wall region were studied (i.e. r/R = 0.00, 0.74, 0.81, 0.87, 0.92, and 0.98).
3.2. Data Processing
Solid concentration signals were used to compute correlation integrals using FORTRAN 2008 codes by employing Equation (2) for the preset hyperspherical radius, r, by varying the number of embedding dimensions from 2 ≤ m ≤ 25. The plots of correlation integral, ln(Cr), versus hypersphere radius, ln(r), were plotted in the suitable ranges of r for each signal to establish a notable scaling region. Visual inspection method were used to identify the scaling region where by a relatively straight section of the ln(Cr) − ln(r) curve were selected thereby removing the remaining portion of the curve. Then the scaling region was plotted for different radial positions in the wall region at different axial elevations and operating conditions.
3.3. Determination of Scaling Region from Correlation Integrals
To determine scaling regions, the following procedure were used: (a) generation of correlation integrals for different number of embedding dimensions (m = 2 to 25) at fixed operating conditions, (b) generation of correlation integrals at fixed number of embedding dimension, m, and at different operating conditions and locations, (c) identification of number of scaling regions and their respective ranges for each correlation integrals, and (d) plotting scaling regions on ln(Cr) − ln(r) plane to identify their location and analysing them basing on their number, slope, location and operating conditions. Procedures (a) to (d) were thus referred to as mapping the dynamics of the gas-solid flow using scaling regions from solid concentration time series.
4. Results and Discussion
4.1. Sample Scaling Regions and Their Analysis
Figure 2 shows correlation integral profiles in the first raw with their respective scaling region in the second raw from the entrance section (Z = 1.52 m) of the riser in the wall region at r/R = 0.81 for Ug = 5.5 m/s and Gs = 300 kg/m2s. The
![]()
Figure 2. Labeled correlation integral and its respective scaling region from the entrance section of the riser at r/R = 0.81 for Ug = 5.5 m/s and Gs = 300 kg/m2s.
first column shows correlation integral profiles with their scaling region for selected embedding dimensions, m = 5, 8, 12 and 19 while the second column show correlation integral profiles with their scaling region for embedding dimensions, m, from 2 to 25.
Features of the correlation integral profiles and scaling regions are the non-linear parts which present a region on the reconstructed attractor with very scattered system’s condition points beyond which the attractor ends. The linear part which is the linear section of the correlation integral profile referred to as the scaling region where the correlation dimension of the attractor is computed from. This part presents a region on the reconstructed attractor with dense system’s states points. Further the figure shows the boundary line on the top and the bottom which connects the end points of the scaling region.
The correlation integral and scaling region profiles are the ln(Cr) versus ln(r) curves which indicates how the points of the system’s conditions are distributed on the reconstructed attractor in the phase space. In chaos analysis the attractor is reconstructed from which important information are extracted through various techniques such as analysing correlation integrals and identifying the scaling regions. Then attractor’s parameters are determined which in turn are used to describe or related to gas solid flow dynamics in the riser from which a time series data signals were sampled.
Several studies report the use of scaling regions in describing various phenomenon of the non-linear and chaotic systems such as the gas-solid flow behaviours in circulating fluidized bed riser [1] [9] [10] [12] [20] [21]. However, most of these studies are limited to the identification and use of the scaling region in determining the correlation dimensions of the system’s attractor. This work has extended the study on extracting more detailed information from the scaling regions in various flow development sections of the riser in the centre and the wall region. This study further presents the fact that scaling regions shifts its location along ln(r) axis and change its height along ln(Cr) axis. It also shows the number of scaling regions that can be obtained from the correlation integral. This study has also identified and presented the top and bottom boundaries of the scaling region end points as they change with embedding dimensions. Further this study has presented the effects on the scaling region of operating conditions and location in the riser in terms of radial positions and axial elevations or flow development sections. The study has also been able to identify and locate the multifractal basin which is the region demarcating the two separate scaling regions, i.e. the non-linear middle part of the scaling region separating the top and bottom linear part or scaling region.
From Figure 2 it can be observed that as m increases the line spacing between profiles decreases while the slope of the profiles increases until it saturates to a constant slope. Also the length of the scaling region differs as m changes. The length of the scaling region indicates the size of the attractor in the phase space. The longer the scaling region the larger the attractor of a system’s phase space at a particular embedding dimensions. Also the slope of the scaling region indicates how points of the state’s conditions are scattered on the attractor. High slope indicates very densely distributed points while low slope indicates less dense distribution. Further, some correlation integrals show more than one scaling regions. This indicates more than one gas-solid flow dynamics phenomenon.
Further, using the mapped scaling regions this study have been able to show the increase in the number of scaling region close to the wall (r/R = 0.92) from the entrance section towards the fully developed flow section. This indicates the increase in gas-solid flow dynamic phenomenon. Also results show the horizontal span of the scaling region in some radial positions like (r/R = 0.81) narrows upwards from the entrance section towards the fully developed section especially at which indicates the shrinkage in size of the attractor from the bottom towards the top.
4.2. Mapping the Dynamics in the Entrance Section of the Riser
The correlation integral ln(Cr) profiles with their respective scaling region in the entrance section (Z = 1.52 m) of the riser at the centre and the wall region for Ug = 5.5 m/s and Gs = 300 kg/m2s at different radial positions (r/R = 0.0, 0.81 and 0.98) are presented in Figure 3. Plots show variations of correlation integral with hypespherical radius ln(r) in a series of embedding dimensions, m, from 2 to 25.
Analysis of scaling regions starts by plotting correlation integrals followed by identification of scaling regions obtained by varying embedding dimensions, m, spanning from 2 to 25. Observation of the linear part of correlation integral curves shows that the scaling regions have different locations on the plane according to the embedding dimension. The results shows also that the scaling
![]()
Figure 3. Correlation integrals and the corresponding scaling regions at different radial positions in the entrance section of the riser (at Z = 1.52 m) at Ug = 5.5 m/s and Gs = 300 kg/m2s using different phase reconstruction dimensions.
region concentrates in one region as embedding dimension becomes higher indicating saturation of the phase space. The distance between adjacent correlation integral and scaling region curves decreases as m increases throughout from m = 2 to 25 making them very close towards higher embedding dimensions. From m ≥ 10 the scaling regions are parallel with closer distribution of curves. That is, the linearity of the scaling region becomes constant at higher embedding dimension. This observation is different from results obtained from the numerical studies as reported in [12] where distances between adjacent curves were found to be relatively constant and parallel from m ≥ 6.
The steepness of the curves in the linear section which express the slope of the scaling region were found to increase as the embedding dimension (m) increases. However, the slope of the linear scaling region becomes relatively the same from m = 15. Further it can be seen that as the hyperspherical radius, r, increases the correlation integral increases also. That is, the scaling region shifts from left to right as m increases until saturation. The scaling region exists only in a specific region of the plane before and beyond which it does not exist. This makes the selection of r to be critical for a different time series. Further, it can be seen in Figure 3 that the scaling region end points differ for each embedding dimension. Also, the separation of the scaling region end points is higher at the initial values (ri) than the final values (rf) of the hypespherical radius. The same applies for increasing m.
Further observation of the correlation integrals and scaling regions show that curves at the centre and in the wall region have single S-shape profile with one scaling region for each correlation integral. The scaling region at the centre is located between −7 to −3 on the ln(r) axis while in the wall region at r/R = 0.81 it is located between −4 to −1. At r/R = 0.98 the scaling region is located between −7 to −3 on the ln(r) axis. Vertically the scaling region is span between −6 to −1 on the ln(Cr) axis. It can be also observed that curves in the scaling regions at the centre (r/R = 0.0) are more steeper compared to that in the wall especially at r/R = 0.81.
4.3. Mapping the Dynamics in the Wall Region of the Flow-Development Section of the Riser
Figure 4 shows the correlation integral plots and the corresponding scaling regions in the flow development section (Z = 3.96 m) at the centre and the wall region of the riser for Ug = 5.5 m/s and Gs = 300 kg/m2s.
Results show that the scaling regions have different location on the plane according to the embedding dimension as reported also above. In the flow development section of a high flux riser, the scaling regions indicated multifractal flow dynamics at r/R = 0.81. In this case, for m = 6 to 25, two scaling regions were observed one at the top and the other at the bottom of the correlation integral. Embedding dimension, m ≥ 6, was capable to discern multiple scaling regions indicating that the attractor reconstruction unfolds the dynamics compared to m < 6.
![]()
Figure 4. Correlation integrals and scaling regions at different radial positions in the flow-development section of the riser (at Z = 3.96 m) for Ug = 5.5 m/s and Gs = 300 kg/m2s using different number of embedding dimensions.
For m between 6 and 25, the observed multifractal behaviour leads to double S shaped correlation integrals for each m which manifests into a visible basin when the integrals are plotted together as seen in Figure 4. We define this behaviour as a multifractal basin. This leads to the importance of choosing optimum embedding dimension (m) since m below 6 does not show the multifractal behaviours. As the hyperspherical radius, r, increase the correlation integral increases also until it diminishes forming an S-shape curve as it approaches ln(Cr) = 0.0. Also as r decreases, the value of ln(Cr) decreases until it approaches the minimum value at ln(Cr) = −7 where it level down. Again Figure 4 shows variations in the bottom and the upper limit of the scaling region for each embedding dimension. The figure also shows that, scaling regions have different location on the plane according to the embedding dimension and radial position. The correlation integral profiles at r/R = 0.81 shows significant differences from the centre by showing tendency to form more than one scaling region, that is, multifractal dimensions particularly when 6 ≤ m ≤ 25. The sensitivity analysis for m show that embedding dimension less than 6 (m ≤ 6) does not show the multifractal behaviour as it shows only one linear part.
Correlation integral profiles at r/R = 0.92 differs from that at the centre since at higher m, they form more than one S-shaped profiles especially for m ≥ 15. This leads to the formation of more than one corresponding scaling regions. At higher embedding dimensions, say for m ≥ 15, multiple scaling regions become more distinct up to four towards m = 25. The observed multiple scaling region indicates presence of the multifractal flow behaviours. This behaviour could not be observed for lower embedding dimensions such as m ≤ 15.
Figure 5 presents correlation integrals and their respective scaling regions at
![]()
Figure 5. Correlation Integrals and scaling region at different radial positions for Z = 3.96 m, Ug = 5.5 m/s and Gs = 300 kg/m2s using different embedding dimensions.
different radial positions in the developing flow section (Z = 3.96 m) at the center and in the wall region of the riser for different embedding dimensions when the operating conditions were fixed at Ug = 5.5 m/s and Gs = 300 kg/m2s.
From the scaling regions, it can be seen that their slopes decreases towards the wall indicating that correlation dimension decreases towards the wall. The scaling regions at the centre are longer than the profiles in the wall region where the shortest scaling regions were observed for the profile close to the wall at r/R = 0.98. Towards the wall, more than one scaling region were observed, changing from single S-shaped correlation integrals, to multiple S-shapes within one curve, behaviour which is more pronounced for m = 15 and 25. For m = 5, the signals show more than one scaling region at r/R = 0.87 and 0.92. This behaviour is also shown when m = 15 and 25 in the wall especially close to the wall at r/R = 0.98. For r/R = 0.98, the number of scaling regions increased from one at m = 5 to two and three at m = 15 and 25, respectively. The number of fractals or scaling regions increases with embedding dimensions, m, showing that the attractor becomes fully unfolded at higher m. Where multifractal behaviour is exhibited, e.g., at r/R = 0.98; the slope of scaling regions increases along the ln(r) axis, but also there is a vertical shift of the scaling region. The correlation dimension increases along ln(r) being highest towards high ln(r) values, or towards the right. For r/R = 0.0, only one scaling region was observed regardless of increasing m although its slope increases towards m = 15 and remains constant until m = 25. Moreover, increasing m, the scaling region(s) at r/R = 0.0, shifts to the right at higher r, on the ln(Cr) − ln(r) plane indicating that the attractor expands with increasing trajectory distances. When compared to other studies which reported the maximum correlation dimension, such as in [8] and others, this study reveals multiple scaling regions with different distinct slopes or correlation dimensions. This observation reveals a detailed view of the multiphase flow behaviour at the wall of a high-flux riser.
4.4. Mapping the Dynamics in the Fully-Developed Flow Section of the Riser
4.4.1. Effect of Radial Position
The scaling regions in the fully developed section at Z = 9.42 m at the centre region of the riser (r/R = 0.0) and in the wall region at r/R = 0.81 and 0.98 for Ug = 5.5 m/s and Gs = 300 kg/m2s are presented in Figure 6. The plot shows the variation of correlation integral with hypespherical radius ln(r) and the respective scaling region at different embedding dimensions, m, spanning from 2 to 25. The behaviour of the correlation integral and scaling regions for different radial positions gives an insight of the gas-solid flow dynamics in the riser.
Results show that the scaling regions have different location on the plane according to the embedding dimension and radial positions. In Figure 6 it can be seen that the end points of the scaling region differ for each embedding dimension and the separation of the scaling region end points is higher at the initial values (ri) than the final values (rf) of the hypespherical radius, where the scaling region does not change location as m increases. Also the scaling regions are less steep in the wall region as compared to the profiles at the centre.
Results in Figure 6 shows one scaling region at r/R = 0.0 and in the wall region at r/R = 0.81 with single S shaped correlation integrals for each m. As the
![]()
Figure 6. Correlation integrals and scaling regions at different radial positions in the fully-developed flow section of the riser (at Z = 9.42 m) for Ug = 5.5 m/s and Gs = 300 kg/m2s using different number of embedding dimensions.
hyperspherical radius, r, increase the correlation integral increases until it diminishes forming an S-shape curve as it approaches ln(Cr) = 0.0 where it levels up. Also as r decreases, the value of ln(Cr) decreases until it approaches the minimum value at ln(Cr) = −7 where it level down. The plot also shows that, scaling regions have different location on the plane according to the embedding dimension and radial position. The Scaling region and correlation integral profiles at r/R = 0.81 have S-shaped profiles similar to that at the centre but with low slope comparatively. Curves are not evenly distributed where the distances between curves decreases as m increases from m = 2 to 25 making them very closer towards higher embedding dimensions. This indicates the saturation of the reconstructed attractor. Further, slopes of the scaling region increases as m increases and then becomes relatively constant at higher embedding dimension towards m = 25. Close to the wall (r/R = 0.98), two scaling regions are observed for embedding dimensions from m = 2 to 25 which leads to the double S shaped correlation integrals which again manifests into a visible basin when the integrals are plotted together. These scaling regions indicate presence of multifractal flow dynamics.
4.4.2. Effect of Gas Velocity in Different Radial Position
The mapping in Figure 7 shows the correlation integrals and their respective scaling regions when the embedding dimensions, m = 5, in the developing flow section (Z = 3.96 m) at the centre (r/R = 0.0) and the wall region (r/R = 0.81 and 0.98) for different gas velocities of Ug = 5.5, 8 and 10 m/s with Gs = 300 kg/m2s. The figure shows that the correlation integrals/scaling region occupy different locations along ln(r) axis and has different slopes at different gas velocities. At
![]()
Figure 7. Correlation integrals and scaling region in the fully developed flow section (at Z = 3.96 m) for m = 5 and operating conditions, Ug = 5.5, 8, and 10 m/s and Gs = 300 kg/m2s.
the centre (r/R = 0.0), single scaling region is observed which comes from a clear single S-shaped correlation integral profiles when the riser is operated at all three gas velocities. The scaling regions formed at the centre have steep slopes compared to those in the wall region for all gas velocities. The increasing number of scaling regions when the gas velocity is high, i.e. Ug = 10 m/s, indicates formation of multifractal dynamics at r/R = 0.81 and 0.98.
The formation of multiple scaling regions is also shown in Figure 8 where the correlation integrals and their respective scaling regions are presented when the embedding dimensions, m = 25, in the fully developed flow section (Z = 9.42 m) at the centre (r/R = 0.0) and the wall region (r/R = 0.81 and 0.98) for different gas velocities of Ug = 5.5, 8 and 10 m/s with Gs = 300 kg/m2s. It can be observed that the correlation integrals/scaling region have different locations along ln(r) length and different slopes at different gas velocities. At the centre (r/R = 0.0) a clear single scaling region was observed from a clear single S-shaped correlation integral profiles for all three gas velocities. The scaling regions at the centre have steep slopes compared to those in the wall region for all gas velocities. The formation of multiple S-shaped correlation integral profiles increases the number of scaling regions which indicates multifractal flow dynamics in the wall region as shown at r/R = 0.81 and 0.98 for all gas velocities. At Ug = 5.5 m/s, a single scaling region was observed for r/R = 0.0 and 0.81, while at Ug = 8.0 m/s and 10 m/s double scaling regions are observed at r/R = 0.81. At the wall, r/R = 0.98, when the riser is operated at all gas velocities the multiple scaling region is observed with lower gas velocity having up to three distinct scaling regions. Such behaviour can not be observed when the analysis is done using single value of correlation
![]()
Figure 8. Correlation integrals and scaling region in the fully developed flow section (at Z = 9.42 m) for m = 25 and the operating conditions, Ug = 5.5, 8, and 10 m/s and Gs = 300 kg/m2s.
dimension. The correlation integrals at r/R = 0.98 have no clear S-shaped profiles with multiple scaling regions suggesting multifractal gas-solid flow behaviours.
4.5. Comparing the Scaling Regions in Different Flow Development Sections of the Riser
The comparison of scaling regions in three different flow development sections in the wall region and at the centre when the riser is operated at the gas velocity, Ug = 5.5 m/s and solid mass flux, Gs = 300 kg/m2s is shown in Figure 9. At the centre (r/R = 0.0), profiles have single scaling region for all sections indicating highly uniform flow behaviours. Profiles in the wall region, starting from r/R = 0.81 in the developing flow section (Z = 3.96 m) towards the wall (r/R = 0.92) shows multiple scaling region. Formation of multiple scaling regions is more observed close to the wall for all flow development sections especially at higher embedding dimensions. This may imply presence of multiple gas-solid flow dynamic phenomena resulting from solid-solid interactions, gas-solid interactions, solid wall interactions, gas-gas molecules interactions, gas-wall interactions and solids back-flow. The influence of the exit shape and solids back-flow at the top of the riser and close to the wall is shown by the change of location and size of the scaling regions towards the top. At Z = 9.42 m and r/R = 0.92 the scaling region is small and more concentrated towards the origin of the ln(r) − ln(Cr) plane. The reduction of the size of the scaling region towards the wall may also
![]()
Figure 9. Comparison of the scaling regions from different flow development sections of the riser for Ug = 5.5 m/s and Gs = 300 kg/m2s.
indicate contraction of the system’s attractor.
In Figure 9 the last two columns presents the scaling regions at different scale but from the same radial position (r/R = 0.92) along different flow development sections. The last column are drawn using large scale in order to unfold different features which are not visible when drawn using small scale like the presence of multiple scaling regions.
Further observations show variations in locations and limits of the scaling region throughout the riser sections and regions. For instance, scaling regions at r/R = 0.81 along different flow development sections occupy different locations along the ln(r) axis for all sections. In the entrance section (Z = 1.52) it is located between 0.0 to −4, while in developing flow and fully developed flow sections they are located between −1 to −5 and −4 to −7 respectively. Vertically along the ln(Cr) axis, the scaling regions are located between −1 to −6 for the centre and in the wall region at r/R = 0.81 for all sections.
Results further show that slopes of the scaling regions in the wall region are relatively lower than those at the centre and hence low correlation dimensions compared to that at the centre. The lowest slopes are observed in the developing flow section at r/R = 0.81 and in the developed flow section at r/R = 0.92. Most of the slopes of the scaling regions increase as the embedding dimensions increases up to where it becomes relatively constant at higher embedding dimensions. Also, the distances between curves decreases as embedding dimensions increases making profiles to become closer until the distances becomes relatively constant at higher embedding dimensions. These observations are shown at the centre and in the wall region at r/R = 0.81 for all sections. Such observations indicate saturation of the reconstructed attractor.
5. Conclusions
Gas-solid flow dynamics in the high-flux CFB riser were studied by analysing the scaling regions at different radial position and axial elevations for different operating conditions of gas velocity (Ug) and locations along the ln(r) axis. The number and length of scaling regions, slopes, presence of multifractal basins, and shifting tendency along ln(r) axis were assessed and discussed. Based on the results and discussion the following conclusions can be made:
1) Scaling regions have different location on the plane according to the particular spatial location within the riser and operating conditions.
2) As the number of embedding dimensions increases, spacing between scaling regions decreases until it saturates towards higher embedding dimensions.
3) The slope of scaling regions increases as the number of embedding dimensions (m) increases until it saturates and becomes constant at higher embedding dimensions.
4) Towards the wall, the slope of scaling regions decreases while the number of scaling regions increases.
5) The span of the scaling region is wider at the initial values (ri) than the final values (rf) of the hyperspherical radius.
6) The scaling regions in the developing flow section (Z = 3.96) and the wall region (r/R = 0.81 and 0.98) show multifractal behaviour for each embedding dimension which manifests into a visible basin defined as multifractal basin.
7) The end points of the scaling region for each profile differ from each other as the number of embedding dimension changes.
However, this study is not exhaustive and therefore further studies are recommended on risers of different diameters and heights that are operated at different conditions of solid flux (low and high) and gas velocities for comparison. But also further studies are recommended using time series of different signal types like pressure fluctuations.