Economic Model Predictive Control for Hot Water Based Heating Systems in Smart Buildings ()
1. Introduction
Setting a target of 100% renewable energy including transport sector by 2050 and 50% of electricity consumption supplied by wind in 2020 in Denmark, under the European 20-20-20 target regarding renewable energy policies [1], provides power systems with new challenges due to renewable energy sources fluctuating nature which calls for additional flexibility on the demand side. In the European Union, buildings are responsible for 40% of total energy consumption including approximately 20% absorbed in heating [2], which can be effectively used in the demand side management (DSM) strategy as a shiftable load.The electricity prices can reflect surplus or deficiency in electricity supply and also the low prices can indicate the high renewable energy penetration in Denmark.
The EMPC is a validated strategy in designing smart buildings’ control and has been studied thoroughly in the recent years. An MPC-based scheduling algorithms developed in [3] for the building energy management system to exploit the thermal mass of the building as well as the non-thermal appliances flexibility to incur energy savings. A pilot study in [4] showed that energy savings and load shifting can be achieved by applying EMPC for electric heaters consumption utilizing a residential building mass as heat storage.
Although the Thermal Energy Storage (TES) is a very potential powerful instrument in DSM programs [5], and the efficiency of the whole system can be extremely enhanced by using heat pumps as energy efficient heating equipment; but this combination has not been studied intensively in the DSM strategies. A study in [6] analyzed heat pump coupled with TES under a DSM strategy designed to flatten the electricity load curve by switching off the heat pump during specific peak hours.
Particularly in this paper we studied a system which consists of an ASHP incorporated with a hot water tank as active TES connected to hot-water radiators utilizing the building mass as passive energy storage. The building model used in this paper is discussed in [4], and the stratification phenomenon is considered in the TES model. Based on the dynamic power price signals and the weather forecast, EMPC optimizes both the ASHP electricity consumption and the building heating consumption; the system’s energy consumption is compared with some reference cases.
The rest of this paper is organized as follows: The system models are introduced in Section 2; the EMPC algorithm for the studied system is developed in Section 3; the corresponding results are shown in Section 4. Finally, the conclusion is drawn in Section 5.
2. Modeling
The heating units in the building are hot-water radiators distributed among the rooms and fed by hot water via inlet electro-valves which can control the water flow rate. The building model was developed in [4], what-so-called TiTe model as a state space model that considers the building envelope temperature as well as the indoor air temperature.
2.1. ASHP Model
The ASHP heat output rate Qh can be calculated by Equation (1) where Pel is the ASHP electric power consumption.
 (1)
(1)
The model considers the air source temperature dependency in a linearized relation. Then the COP and Qh can be given by Equations (2) and (3), where COP0, Q0, a1 and b1 are identified according to manufacturer’s specifications [7].
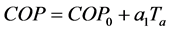 (2)
(2)
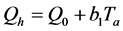 (3)
(3)
2.2. TES Model
Thermal stratification is an important concept when dealing with hot water storage, which results from the density difference between the warm water and the cold water causing the hot water to ascend to the top. Studies as in [8] showed that improving the thermal stratification can significantly improve the system efficiency. The TES model is developed based on the concept illustrated in [9]. Figure 1 shows a stratified tank with L meters height and N layers. The hot water is fed from the production side to the top layer with  mass flow rate at temperature Thp,out ˚C. The heat load is supplied from the top layer with
flow rate of and the return is to the bottom layer to avoid thermal mixing.
mass flow rate at temperature Thp,out ˚C. The heat load is supplied from the top layer with
flow rate of and the return is to the bottom layer to avoid thermal mixing.
The heat balance can be given by Equation (4). Where m is the mass of the hot water; Cp is the water thermal capacity, and Tw,i is the water temperature in the ith layer.
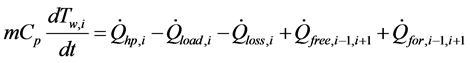 (4)
(4)
Beside the ASHP heat input , the load consumption
, the load consumption 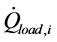 and the losses to the environment
and the losses to the environment 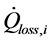 the term
the term 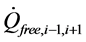 represents the amount if heat exchanged in layer i with the surrounding layers i − 1 and i + 1 by natural convection and thermal conduction. In the simplest approximation, this can be summarized in effective vertical heat conductivity
represents the amount if heat exchanged in layer i with the surrounding layers i − 1 and i + 1 by natural convection and thermal conduction. In the simplest approximation, this can be summarized in effective vertical heat conductivity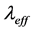 , and the heat flow between layer i − 1 and i, or from i to i + 1. The net heat flow for layer i of height z and cross section Aq results in the difference of the two heat flows. The effective heat conductivity
, and the heat flow between layer i − 1 and i, or from i to i + 1. The net heat flow for layer i of height z and cross section Aq results in the difference of the two heat flows. The effective heat conductivity 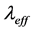 can be between 1 - 1.5 W/mK.
can be between 1 - 1.5 W/mK. 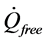 is calculated by Equation (5). The forced convection is represented by
is calculated by Equation (5). The forced convection is represented by 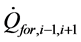 and can be calculated by Equation (6), where
and can be calculated by Equation (6), where  is the mass flow rate.
is the mass flow rate.
![]()
Figure 1. Stratified hot water tank with N layers.
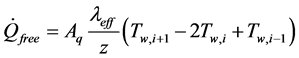 (5)
(5)
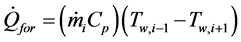 (6)
(6)
So Tw,i can be calculated downward successively according the Equation (7).
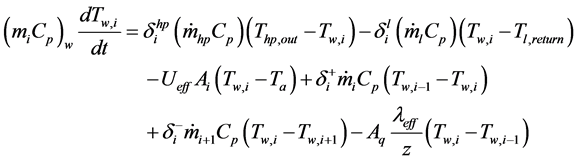 (7)
(7)
where:
![]() and
and ![]()
![]() ,
, ![]() ,
, ![]() and
and ![]() are control parameters as follows:
are control parameters as follows:
ASHP is connected to the top layer, and the heat load is returned to the bottom layer:
![]()
Energy input from layer i − 1 to layer i; and the energy input from layer i + 1 to i:
![]()
2.3. Hot-Water Radiator Model
The hot-water radiator heat transfer rate and the hot water mass flow rate are calculated based on Equations (8) and (9) respectively. The design values are based on the EN 442 [10] and the manufacturer’s technical manual. Where ![]() is the radiator design heat transfer rate;
is the radiator design heat transfer rate; ![]() is the design surface temperature;
is the design surface temperature; ![]() is the design indoor temperature;
is the design indoor temperature; ![]() is the radiator return temperature;
is the radiator return temperature; ![]() is the flow temperature, n is the correction factor and
is the flow temperature, n is the correction factor and ![]() is the mass flow rate.
is the mass flow rate.
![]() (8)
(8)
![]() (9)
(9)
3. Case Study
The studied system is shown in Figure 2; the ASHP extracts the heat from the air and supplies the TES with hot water. Upon request, the hot water flows through the radiators transferring the required heat by convection to the ambient in each floor in the building, then the cold water flows back to the TES.
In order to utilize both storage capacities, i.e. the building mass and TES, the
![]()
Figure 2. A generic description for the studied system.
EMPC algorithm which is shown in Figure 3 solves two sequential optimization problems for every sampling time within the prediction horizon. The PFH3 algorithm determines the radiators’ output to supply the building with the required heat; it is the same as developed in [4]. The second algorithm is to optimize the ASHP electric power consumption to set the TES temperature to the optimal temperature within the operating boundaries.
The objective function of the ASHP optimization is given by Equation (10).
![]() (10)
(10)
where: ![]() is the price vector for the prediction horizon N sampled every k period of time.
is the price vector for the prediction horizon N sampled every k period of time. ![]() is the ASHP electric consumption, which is the manipulated input within the operational limits
is the ASHP electric consumption, which is the manipulated input within the operational limits ![]() and
and![]() .
. ![]() is a nonlinear function which represents the temperature of the stored water for the TES top layer, and it is calculated using the TES in Equation (7).
is a nonlinear function which represents the temperature of the stored water for the TES top layer, and it is calculated using the TES in Equation (7).
Particularly, ![]() is used as the manipulated variable.
is used as the manipulated variable. ![]() is the minimum stored temperature, in this study the boundary is optimized to meet the demand at a every certain time and not fixed to a constant value; this minimum value is calculated by utilizing the radiator model described in Equation (8) to calculate the optimal
is the minimum stored temperature, in this study the boundary is optimized to meet the demand at a every certain time and not fixed to a constant value; this minimum value is calculated by utilizing the radiator model described in Equation (8) to calculate the optimal ![]() and it should be sufficient to the maximum required load among the floors.
and it should be sufficient to the maximum required load among the floors. ![]() is the maximum boundary and set to 100˚C temperature to keep the water from being evaporated.
is the maximum boundary and set to 100˚C temperature to keep the water from being evaporated.
4. Simulation Results
The system is simulated using day-ahead electricity market price signals and weather data from the local weather station records for 5 days in winter; a reference case is a traditional PID system realized by setting the low and high temperature constraints at the same values to follow the lower comfort band temperature in the building using electric heaters without TES. Also the system is compared to another case in which the ASHP is directly connected to the radiators without the TES, this case is simulated using the PFH3 developed in [4] by utilizing the ASHP model.
![]()
Figure 3. Functional block diagram for EMPC system.
Figure 4 shows the radiators optimal power consumption, the price signal (bottom plot) and indoor temperature (top plot); it is obvious that the radiators consumption is shifted to the low price periods while the indoor temperature is controlled within the comfort constraints (dotted lines). In Figure 5 the bottom plot shows the ASHP optimal electric power consumption shifted to the low price periods; and the temperature of the top layer in the TES (top plot), the lower red dotted curve is the optimal flow temperature calculated from the optimal heat output resulted from PFH3 for every sample time; we can observe the tank top layer temperature is kept within these varying constraints, even though the maximum temperature in the tank is limited to the ASHP maximum flow temperature (55˚C).
The savings are evaluated based on the reference case (the traditional PID) for 10 days simulation and shown in Table 1. Using the EMPC with electric heaters achieved 4.3% savings over the traditional PID control which reflects the effectiveness of shifting the loads intelligently to the low price periods. Using ASHP with hot-water radiators; the savings jumped significantly to 73.6% over the reference case when using ASHP with hot-water radiators because of the ASHP principle of operation. The studied system in this paper; incorporating the TES with the ASHP saved 7.9% more where the total saving incurred is 81.5% over the reference case.
5. Conclusion
The simulation results of the EMPC algorithms effectively showed a successful shift for the electricity demand based on the price where the power consumption is shifted to the low price periods in the study case while the systems states are kept within the limits. In addition, for households, the monetary value of the
![]()
Figure 4. Indoor temperature and optimal heaters’ output.
![]()
Figure 5. Simulation results for the ASHP and TES.
![]()
Table 1. Energy costs for each scenario and savings based on the reference.
energy savings is small relative to the complexity of the system and the cost of the equipment, so the payback period for this system could be very long for the small buildings with small heat loads; for the future work, a business case could be developed by assuming an agent between the consumer level and the grid operators; this agent can aggregate all the distributed energy sources’ flexibility and provide ancillary services to the grid operators.