On Optimal Sparse-Control Problems Governed by Jump-Diffusion Processes

Beatrice Gaviraghi¹, Andreas Schindele¹, Mario Annunziato², Alfio Borzì¹

¹Institut für Mathematik, Universität Würzburg, Würzburg, Germany.
²Dipartimento di Matematica, Università degli Studi di Salerno, Fisciano (SA), Italy.

DOI: 10.4236/am.2016.716162                

Abstract

A framework for the optimal sparse-control of the probability density function of a jump-diffusion process is presented. This framework is based on the partial integro-differential Fokker-Planck (FP) equation that governs the time evolution of the probability density function of this process. In the stochastic process and, correspondingly, in the FP model the control function enters as a time-dependent coefficient. The objectives of the control are to minimize a discrete-in-time, resp. continuous-in-time, tracking functionals and its L2- and L1-costs, where the latter is considered to promote control sparsity. An efficient proximal scheme for solving these optimal control problems is considered. Results of numerical experiments are presented to validate the theoretical results and the computational effectiveness of the proposed control framework.

Keywords

Jump-Diffusion Processes, Partial Integro-Differential Fokker-Planck Equation, Optimal Control Theory, Nonsmooth Optimization, Proximal Methods

1. Introduction

In this work, we tackle the issue of controlling a stochastic process by following an alternative approach already proposed in [9] - [11] , where the problem is reformulated from stochastic to deterministic. The key idea of this strategy is to focus on the probability density function (PDF) of the considered process, whose time evolution is modeled by the Fokker-Planck (FP) equation, also known as the Kolmogorov forward equation. The FP control approach is advantageous since it allows to model the action of the control over the entire space-time range of the underlying process, which is characterized by the shape of its PDF.

In the case of our JD process, the FP equation takes the form of a PIDE endowed with initial and boundary conditions. While the Cauchy data must be the initial distribution of the given random variable, the boundary conditions of a FP problem depend on the considered model. For the derivation of the FP equation and a discussion about boundary conditions, see [12] - [14] . Starting from the controlled stochastic differential model, the coefficients of the FP equation and thus the control mechanism are authomatically determined and thus an infinite dimensional optimal control problem governed by the FP PIDE related to a JD process is obtained. Since the control variable enters the state equation as a coefficient of the partial integro-differential operator, the resulting optimization problem is nonconvex.

This paper is organized as follows. In the next section, we discuss the functional setting of the FP problem modeling the evolution of the PDF of a JD stochastic process. In Section 3, we formulate our optimal control problems. Section 4 is devoted to the formulation of the corresponding first-order optimality systems. In Section 5, we discuss the discretization of the state and adjoint equations of the optimality system. In Section 6, we illustrate a proximal method for solving our optimal control problems. Section 7 is devoted to presenting results of numerical tests, including a discussion on the robustness of the algorithm to the choice of the parameters of the optimization problem. A section of conclusions completes this work.

2. The Fokker-Planck Equation of a Jump-Diffusion Process

In this section, we introduce a JD process and the corresponding FP equation that models the time evolution of the PDF of this process. Further, we discuss well-posed- ness and regularity of solutions to our FP problem.

We consider a time interval 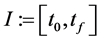and a stochastic process 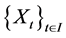with range in a bounded domain. We assume that the set 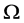is convex with Lipschitz boundary. The dynamic of X is governed by the following initial value problem

(1)

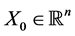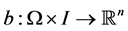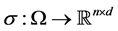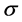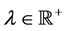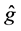where is a random variable with known distribution. The functions and represent the drift and the diffusion coefficients, respectively. We assume that is full rank. Random increments to the process are given by a Wiener process and a compound Poisson process. The rate of jumps and the jump distribution are denoted with and, respectively.

Define,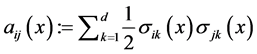. Since 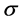is full rank, a is posi-

tive definite, and hence there exists 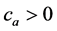such that

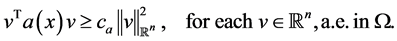(2)

In this work, we consider a stochastic process with reflecting barriers. This assumption determines the boundary conditions for the FP equation corresponding to (1), see below. Define and, and denote with f the PDF of the process given by (1). It is known [12] [13] that the time evolution of f is modeled by the following FP of PIDE type

(3)

where the differential operator and the integral operator are defined as follows

(4)

and

(5)

respectively. The definition of g in (5) takes into account the presence of reflecting barriers and the dependence on the jump amplitude, as we discuss later.

Notice that the differential operator can be rewritten as follows

where

(6)

and

(7)

for each. The function F in (6) represents the flux of the differential operator L, and −F is known in the literature as the probability current in case of stochastic processes without jumps [13] .

The PDF f of X in (1) in the bounded domain is obtained by solving (3), endowed by suitable initial and boundary conditions. In our setting, the initial data represents the PDF of the initial random variable. The choice of a bounded domain with reflecting barriers results in the following zero-flux boundary conditions for the FP model

(8)

where is the unit outward normal on.

Notice that the flux F corresponds to the differential part of the FP equation, that is, to the drift and diffusion components of the stochastic process. In order to take into account the action of a reflecting barrier on the jumps, we consider a suitable definition of the kernel g, which can be conveniently illustrated in the one-dimensional case as follows.

Consider and. The kernel g in (5) takes the following form

(9)

where H is the Heaviside step function defined by

We normalize g and such that

(10)

The next remark motivates the choice of the boundary conditions (8) and of the condition (10).

Remark 2.1. Assume (8) and (10). Provided that is a PDF in, then the solution to our FP problem satisfies the following conservation equation

That is, the total probability over the space domain at each time is preserved, in the sense that

Our FP problem is stated as follows

(11)

Next, we recall some definitions concerning the functional spaces needed to state the existence and uniqueness of solutions to (11). The space refers to the functions that are continuous in and it is endowed with the supremum norm. Let be a constant,. The space refers to the functions that are Hölder continuous on, with Hölder exponent with respect to the space variable. The space denotes all the functions that are bounded on, up to a set of zero measure. The spaces and are defined as follows

(12)

These spaces are endowed with the following norms

where denote multi-indeces.

We assume that the coefficients a and b in (4) satisfy the following conditions

(13)

for each.

Notice that a and b must be defined on the closure due to their role in the boundary conditions in (11). We assume that the following condition is satisfied

(14)

with and for.

We have the following theorem [29] .

Theorem 2.1. Assume. Let the coefficients a and b in L in (4) and that g satisfy the assumptions (13) and (14), respectively. Then, for given, the initial-boundary value problem (11) admits a unique solution.

Proof. See [29] .

Remark 2.2. Provided that is also a PDF, it follows by standard arguments [29] that for each.

Consider the following spaces,. We denote with the dual space of V and with their canonical pairing. We consider the following Gelfand triple, that exploits the natural isomorphism between a Hilbert space with his dual. Each embedding is dense and continuous [17] .

Given the interval and an arbitrary Banach space Z, we define the following spaces

(15)

(16)

which are also Banach spaces [17] equipped with the following norms

respectively. We consider the following space

(17)

which is a Hilbert space [17] with respect to the scalar product defined as follows

With this preparation, we can recall the following theorem [17] .

Theorem 2.2. The embedding is continuous. Therefore, every coincides with an element of, up to a set of null measure.

The following proposition provides a useful a priori estimate of the solution to (11).

Proposition 2.3. Let, , and g satisfies (14). Then if f is a solution to (11), the following inequality holds

(18)

Proof. Consider the H inner product of the equation in (11) with f. Exploiting the properties of the Gelf and triple, we have

(19)

We make use of the following fact [17] ,. The terms on the right-hand side in (19) are recast as follows.

First, we exploit the zero-flux boundary conditions in (11) and the coercivity of a as given in (2). Moreover, we make use of the following Cauchy inequality

which holds for each and. Integrating by parts and recalling the definition of F in (6), we have

We choose, where is defined in (2), and define

.

We have thanks to (13).

Therefore we have

(20)

Recalling the definition of I in (5) and defining, we have

Since is bounded, we have

Therefore,

(21)

Define. Note that c is a bounded time-dependent function. The estimates in (20) and (21) allow us to write (19) as follows

By applying the Gronwall inequality, we have

(22)

Next, we outline how to obtain an upper bound of. We integrate (2) over and then recall the definition of F in (6). We have

where we used the PIDE and the boundary condition of the FP problem in (11). Proceeding as above, we obtain

with. This last estimate, together with (22), proves that

up to a redefinition of the constant. The estimates of the other addends in (18) follow after some calculation with arguments as in [9] [17] .

Proposition 2.4. Assume (13) and. Then the unique solution to (11) belongs to, with. Moreover,.

Proof. The statement follows from the a priori estimates of Proposition 2.3 and Theorem 2.2.

We define, where is the initial data in (11). The initial-boundary value problem (11) can be stated as, where the map is defined as follows

(23)

with F and I defined in (6) and (5), respectively.

3. Two Fokker-Planck Optimal Control Problems

In this section, we define our optimal control problems governed by (23) and prove the existence of at least an optimal solution.

We consider a control mechanism that acts on the drift function by means of a time-dependent control. Therefore we refer to (23) as. We assume that b is a smooth function of its arguments and that assumption (13) is fulfilled. We remark that a time-dependent control function is a natural choice considering that it originates from the stochastic differential model where the time is the only independent variable.

We assume the presence of control constraints given by, with. We denote

(24)

(25)

Remark 3.1. The subset is nonempty, closed, and convex.

Let and be positive constants. We consider the following objective

(26)

The term in (26) represents a tracking objective that involves the expectation value of, , and a desired trajectory or a discrete set of values (e.g. measurements). We investigate the following two cases.

1) Given a set of values at different times, , we have

(27)

2) Given a square-integrable function, we have

(28)

The norms in (26) are defined as follows

Remark 3.2. The choice of a bounded time interval I ensures that the L¹-norm is finite whenever.

Remark 3.3. The functional is convex and continuous with respect to in the norm.

We investigate the following optimal control problem (s)

(29)

In order to discuss the existence and uniqueness of solutions to (29), we consider the control-to-state operator, that maps a given into, where satisfies. Note that the definition of in (25) ensures that b satisfies (13). Because of Theorem 2.1, the operator is well defined.

The next proposition can be proved by using standard arguments [9] [17] .

Proposition 3.1. The mapping solution to (11) is Fréchet differentiable and the directional derivative satisfies the follow- ing initial-boundary problem

(30)

where b is the drift in (1) and F is defined in (6).

The constrained optimization problem (29) can be transformed into an unconstrained one as follows

(31)

where is the so-called reduced cost functional.

The solvability of (31) is ensured by the next theorem, whose proof adapts techniques given in [30] [31] and [17] .

Theorem 3.2. There exists at least one optimal pair that solves (29), such that solves (31) and.

Proof. The functional in (31) is bounded from below and therefore we can define. Let be a minimizing sequence, such that.

We have that is a convex, closed, and bounded subset of the reflexive Banach space. Hence, is weakly sequentially compact and we can extract a subsequence such that.

The weakly lower convergent sequence gives rise to the sequence, defined by. Since the embedding is

compact, there exists a subsequence and such that

converges strongly to. The fact follows from standard arguments. Note that each couple satisfies by definition. Next, we want to

pass to the limit in.

Thanks to the estimate (18) in Proposition 2.3, the sequence is bounded in and therefore weakly convergent to. Define. The boundedness of B as in (7) and the smoothness of b with respect to u together with (18), en-

sures that and converge weakly to and

, respectively, where the norm in has been considered. The weak convergence of to follows from similar arguments [31] . These observations lead to the conclusion that the limit solves (11), with. Therefore, the constraint is satisfied.

Moreover, the convexity of ensures that

and therefore the pair is a minimizer for the problem (29).

Remark 3.4. The uniqueness of the control can not be stated a priori since is non convex.

4. Two First-Order Optimality Systems

We follow the standard approach [17] [23] [32] of characterizing the solution of our optimal control problem as the solution to first-order optimality conditions that constitute the optimality system.

Consider the reduced problem (31) and write the reduced functional as, , where

(32)

Remark 4.1. The functional is smooth and possibly nonconvex, while is convex and nonsmooth.

The following definitions are needed in order to determine the first-order optimality system. If is finite at a point u, the Fréchet subdifferential of at u is defined as follows [32] . We have

(33)

where is the dual space of. Any element is called a subgradient. In our framework, we have

since is Fréchet differentiable at u; this follows from standard arguments [17] [30] . Moreover, for each, it holds that; see [26] .

The following proposition gives a necessary condition for a local minimum of.

Proposition 4.1. If, with and given by (4.1), attains a local minimum in, then

or equivalently

Proof. Since is convex, , for each and. Since is a local minimum, we have

for v sufficiently close to. Exploiting the convexity of, we have

Dividing by and considering the limit, we obtain

(34)

Dividing by and considering the following limit

we conclude that, according to the definiton in (33).

By using results in [22] [32] , we have that (34) implies that each, with a local minimum, satisfies the following inequality

(35)

Moreover, recalling the definition of in (32) and exploiting the isomorphism, the inclusion gives the following

(36)

A pointwise analysis of (35), which takes into account the definition (25) of the admissible controls, ensures the existence of two nonnegative functions that play the role of Lagrange multipliers [17] . The previous considerations lead to the following proposition, that states the optimality system for the reduced problem (31).

Proposition 4.2. The optimal solution of the minimization problem (31) with defined in (32), is characterized by the existence of such that

(37)

We refer to the last three conditions in (37) for the pair as the complementarity conditions.

The differentiability of, and with respect to and allows us to compute in (37) within the adjoint approach. By definition, for each, we have

By considering the total derivative of, we have

Therefore, we obtain

Defining the adjoint variable p as the solution to the following adjoint problem

(38)

we obtain the following reduced gradient

(39)

After some calculation, we have that (38) can be rewritten as the following adjoint system

(40)

where and depend on the choice of D in (27) and (28). When D is given by (27), and, for each. On the other hand, when D is given by (28), and.

The operator is defined as follows

The terminal boundary-value problem (40) admits a unique solution thanks to the assumptions (13) and (14), following the same arguments as in Theorem 2.1 [29] .

The reduced gradient in (39), for given u, f, and p, takes the following form

(41)

The complementarity conditions in (37) can be recast in a more compact form, as follows. We define. For each, we define the following quantity

The complementarity conditions in (37) and the inequalities related to the Lagrange multipliers and, together with the requirement, are equivalent to; see, e.g., [22] .

The previous considerations can be summarized in the following propositions.

Proposition 4.3. (Optimality system for a discrete-in-time tracking functional)

A local solution of (29) with D given by (27) is characterized by the existence of, such that the following system is satisfied

(42)

Proposition 4.4. (Optimality system for a continuous-in-time tracking functional)

A local solution of (29) with D given by (28) is characterized by the existence of, such that the following system is satisfied

(43)

5. Numerical Approximation of the Optimality Systems

In this section, we discuss the discretization of the optimality systems given in (42) and (43). For simplicity, we focus on a one-dimensional case with. We de-

fine, , , and,. The space and time grids

are defined as follows

Notice that a cell-centered space discretization is considered with cells midpoints at, , and cell faces at.

The approximation of the forward and backward FP PIDEs is based on a discretization method discussed in [33] , where a convergent and conservative numerical scheme for solving the FP problem of a JD process is presented. This discretization scheme is obtained based on the so-called method of lines (MOL) [34] . The differential operator in (11) is discretized by applying the Chang-Cooper (CC) scheme [35] [36] . Setting

, and, the discretization

of the differential operator is carried out as follows

where

The zero-flux boundary conditions are implemented referring to the points and. The integral addend is approximated by the midpoint rule. After spacial discretization, the forward FP PIDE problem takes the following form

(44)

where. The matrices and correspond to the CC scheme and to the quadrature rule, respectively. The time integration of (44) is carried out with the combination of the Strang-Marchuk (SM) splitting scheme [37] [38] together with a predictor-corrector scheme [39] . We refer to [40] for a detailed introduction to splitting methods. With this choice, the numerical scheme solving (11) is second-order convergent both in space and time with respect to the norm. Notice that the chosen numerical method for the FP problem must ensure that the PDF solution is nonnegative and that the total probability remains constant along the time evolution. See [33] for all details and numerical analysis results.

The DBO approach results in the following approximations

together with the midpoint quadrature formula applied to in (40). We have the following semi-discretized system

(45)

The time integration of (45) is carried out with the combination of the SM splitting with a predictor corrector scheme, as in (44).

6. A Proximal Optimization Scheme

In this section, we discuss a proximal optimization scheme for solving (31). This scheme and the related theoretical discussion follow the work in [19] [27] . Proximal methods conveniently exploit the additive structure of the reduced objective, and in our framework, we have that the reduced functional is given by the sum of a nonconvex smooth function and a convex nonsmooth function as in (32).

For our discussion, we need the following definitions and properties.

Definition 6.1. Let Z be a Hilbert space and l a convex lower semi continuous function,. The proximity operator of l is defined as follows

Proposition 6.1. Let Z be a Hilbert space and l a convex lower semi continuous function, , with proximity operator. The following relation holds

(46)

where is the subdifferential defined in (33).

Proof. See [27] .

Proposition 6.2. The solution of (31) satisfies

(47)

for each.

Proof. From Proposition 4.7 and by using (46), we have

The relation (47) suggests that a solution procedure based on a fixed point iteration should be pursued. We discuss how such algorithm can be implemented.

In the following, we assume that in (32) has a locally Lipschitz-continuous gradient as follows

(48)

for each, neighborhood of u, with L a Lipschitz continuity constant. It is shown in [28] that (48) implies the following inequality

for each, and hence

(49)

Inequality (49) is the starting point for the formulation of a proximal scheme, whose strategy consists of minimizing the right-hand side in (49). One can prove the following equality

(50)

Recall the definition of in (32). The following lemma gives an explicit expression for the right-hand side in (50).

Lemma 6.3. Let be as in (25). Then

where the projected soft thresholding function is defined as follows

Proof. See [19] .

Based on this lemma, we conclude the following

which can be taken as starting point for a fixed-point algorithm as follows

(51)

where is the local Lipschitz continuity constant defined in (48). Such method has been investigated in [19] [25] [27] . In this work, we apply an extension of (51), which takes for each iteration k the following form

(52)

with. This method has been proposed in [28] . Our inertial proximal method is summarized in the following algorithm.

Algorithm 1 (Inertial proximal method).

Input: initial guess, , , , tolerance tol, Lipschitz constant L.

1) While, do:

(a) Evaluate according to Algorithm 2.

(b) Update until

where

(c) Set.

(d) Compute E according to (42) or (43).

(e) If, break.

(f).

Remark 6.1. The backtracking scheme in Algorithm 1 provides an estimation of the upper bound of the Lipschitz constant in (48), since it is not known a priori. The initial guess for L is chosen as follows. Given a small variation of u, we have

Algorithm 2 (Evaluation of the gradient).

Input:, initial value at time, terminal value at time.

1) Compute, given and.

2) Compute.

3) Evaluate according to (41).

Next, we discuss the convergence of our algorithm, using some existing results [28] [41] .

Proposition 6.4. The sequence generated by (52) satisfies the following properties.

・ The sequence converges in.

・ There exists a weakly convergent subsequence.

Definition 6.2. The proximal residual r is defined as follows

(53)

Proposition 6.12 tells us that in whenever u solves (31). The next proposition establish a connection between the condition and the solution provided by Algorithm 1; see, e.g., [19] .

Proposition 6.5. Let be the sequence generated by Algorithm 1. Then the following holds

7. Numerical Experiments

In this section, we present results of numerical experiments to validate the performance of our optimal control framework. Our purpose is to determine a sparse control such that the expected value of the process X defined by (1) minimizes the quantity defined by (27) and (28).

We implement the discretization scheme and the algorithm described in Section 5. We take and, and assume that the initial probability density function is given,. The compound Poisson process corresponds to the choice and. We take and. In case of (27), we consider. In the case of (28), we take. We choose and.

In the first series of experiments, we consider the setting with and in (32). Further, we do consider constraints on the control. Corresponding to this choice and to the discrete-in-time tracking functional (27), we report in Figure 1 and Figure 2 the solution for the state and the adjoint variables, respectively. On the other hand, using the continuous-in-time tracking functional (28), we obtain the state and the adjoint variables depicted in Figure 3 and Figure 4, respectively.

Also for the case and both tracking functionals, we report in Table 1 and

Figure 1. State variable in the case of the discrete-in-time tracking functional defined in (27), with.

Figure 2. Adjoint variable in case of the discrete-in-time tracking functional defined in (27), with.

Figure 3. State variable in the case of the continuous-in-time tracking functional defined in (28), with.

Figure 4. Adjoint variable in case of the continuous-in-time tracking functional defined in (28), with.

Table 2 the values of the tracking error for different values of the weight. As expected, the tracking improves as the value of this optimization parameter becomes smaller. In Figure 1 and Figure 3, we can see that the optimal control u drives the expected mean value of the PDF towards the mean values given by and, respectively.

Next, we investigate the behavior of the optimal solution considering the full optimization setting, that is, the case when the L¹-cost actively enters in the optimization process, i.e., and the control is constrained by the bounds in (25). For simplicity, we discuss only the case with.

In Figures 5-7, we depict the optimal controls for three different choices of values of and considering the discrete-in-time tracking functional given by (27). In Figures 8-10, we show the optimal controls for three different choices of values of and considering the continuous-in-time tracking functional given by (28). In both cases, we can clearly see that increasing the value of the parameter significantly increases the sparsity of the solution, as expected.

Finally, in the Table 1 and Table 2, we also report values of the tracking error when both the L²- and L¹-costs are considered. For a direct comparison with the first series of experiments, we consider an unconstrained control. We find that already with a small value of, the tracking ability of the optimization scheme worsen for both choices of the tracking functional.

Table 1. Tracking error of the discrete-in-time functional given by (27).

Table 2. Tracking error of the continuous-in-time functional given by (28).

Figure 5. Optimal control with and tracking objective given by (27).

Figure 6. Optimal control with and tracking objective given by (27).

Figure 7. Optimal control with and tracking objective given by (27).

Figure 8. Optimal control with and tracking objective given by (28).

Figure 9. Optimal control with and tracking objective given by (28).

Figure 10. Optimal control with and tracking objective given by (28).

8. Conclusion

A framework for the optimal control of probability density functions of jump-diffusion processes was discussed. In this framework, two different, discrete-in-time and continuous-in-time, tracking functionals were considered together with a sparsity promoting L¹-cost of the control. The resulting nonsmooth minimization problems governed by a Fokker-Planck partial integro-differential equation were investigated. The existence of at least an optimal control solution was proven. To characterize and compute the optimal controls, the corresponding first-order optimality systems were derived and their numerical approximation was discussed. These optimality systems in combination with a proximal scheme allowed to formulate an efficient solution procedure, which was also theoretically discussed. Results of numerical experiments were presented to validate the computational effectiveness of the proposed method.

Acknowledgements

Supported by the European Union under Grant Agreement Nr. 304617 “Multi-ITN STRIKE―Novel Methods in Computational Finance”. This publication was supported by the Open Access Publication Fund of the University of Würzburg. We thank very much the Referee for improving remarks.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Cont, R. and Tankov, P. (2004) Financial Modeling with Jump Processes. Chapman & Hall, London.
[2]	Kou, S.G. (2002) A Jump-Diffusion Model for Option Pricing. Management Science, 48, 1086-1101. http://dx.doi.org/10.1287/mnsc.48.8.1086.166
[3]	Merton, R.C. (1976) Option Pricing When Underlying Stock Returns Are Discontinuous. Journal of Financial Economics, 3, 125-144. http://dx.doi.org/10.1016/0304-405X(76)90022-2
[4]	Pascucci, A. (2011) PDE and Martingale Methods in Option Pricing. Springer, Berlin. http://dx.doi.org/10.1007/978-88-470-1781-8
[5]	Harrison, J.M. and Pliska, S.R. (1983) A Stochastic Calculus Model of Continuous Trading: Complete Markets. Stochastic Processes and Their Applications, 15, 313-316. http://dx.doi.org/10.1016/0304-4149(83)90038-8
[6]	Fleming, W.H. and Soner, M. (1993) Controled Markov Processes and Viscosity Solutions. Springer, Berlin.
[7]	Pham, H. (2009) Continuous-Time Stochastic Control and Optimization with Financial Applications. Springer, Berlin. http://dx.doi.org/10.1007/978-3-540-89500-8
[8]	Yong, J. and Zhou, X.Y. (2000) Stochastic Controls, Hamiltonian Systems and Hamilton-Jacobi-Bellman Equations. Springer, Berlin.
[9]	Annunziato, M. and Borzì, A. (2013) A Fokker-Planck Control Framework for Multimensional Stochastic Processes. Journal of Computational and Applied Mathematics, 237, 487-507. http://dx.doi.org/10.1016/j.cam.2012.06.019
[10]	Annunziato, M. and Borzì, A. (2010) Optimal Control of Probability Density Functions of Stochastic Processes. Mathematical Modelling and Analysis, 15, 393-407. http://dx.doi.org/10.3846/1392-6292.2010.15.393-407
[11]	Roy, S., Annunziato, M. and Borzì, A. (2016) A Fokker-Planck Feedback Control-Constrained Approach for Modelling Crowd Motion. Journal of Computational and Theoretical Transport, 442-458. http://dx.doi.org/10.1080/23324309.2016.1189435
[12]	Cox, D.R. and Miller, H.D. (1977) The Theory of Stochastic Processes. CRC Press, Boca Raton.
[13]	Schuss, Z. (2010) Theory and Applications of Stochastic Processes: An Analytical Approach. Springer, Berlin. http://dx.doi.org/10.1007/978-1-4419-1605-1
[14]	Stroock, D.W. (2003) Markov Processes from K. Itô’s Perspective. Princeton University Press, Princeton. http://dx.doi.org/10.1515/9781400835577
[15]	Borzì, A. and Schulz, V. (2012) Computational Optimization of Systems Governed by Partial Differential Equations. SIAM, Philadelphia.
[16]	Lions, J.L. (1971) Optimal Control of Systems Governed by Partial Differential Equations. Springer, Berlin.
[17]	Tröltzsch, F. (2010) Optimal Control of Partial Differential Equations: Theory, Methods and Applications. American Mathematical Society. http://dx.doi.org/10.1090/gsm/112
[18]	Borzì, A. and Gonzalez, S. (2015) Andrade, Second-Order Approximation and Fast Multigrid Solution of Parabolic Bilinear Optimization Problems. Advances in Computational Mathematics, 41, 457-488. http://dx.doi.org/10.1007/s10444-014-9369-9
[19]	Schindele, A. and Borzì, A. (2016) Proximal Methods for Elliptic Optimal Control Problems with Sparsity Cost Functional. Applied Mathematics, 7, 967-992. http://dx.doi.org/10.4236/am.2016.79086
[20]	Jäger, S. and Kostina, E.A. (2005) Parameter Estimation for Forward Kolmogorov Equation with Application to Nonlinear Exchange Rate Dynamics. PAMM, 5, 745-746. http://dx.doi.org/10.1002/pamm.200510347
[21]	Borzì, A., Ito, K. and Kunisch, K. (2002) Optimal Control Formulation for Determining Optical Flow. SIAM Journal on Scientific Computing, 24, 818-847. http://dx.doi.org/10.1137/S1064827501386481
[22]	Stadler, G. (2009) Elliptic Optimal Control Problems with L1-Control Costs and Applications for the Placement of Control Devices. Computational Optimization and Applications, 44, 159-181. http://dx.doi.org/10.1007/s10589-007-9150-9
[23]	Ulbrich, M. (2011) Semismooth Newton Methods for Variational Inequalities and Constrained Optimization Problems in Function Spaces. SIAM, Philadelphia. http://dx.doi.org/10.1137/1.9781611970692
[24]	Nesterov, Y.E. (1983) A Method for Solving the Convex Programming Problem with Convergence Rate O(1/k2). Soviet Mathematics Doklady, 27, 372-376.
[25]	Tyrrell Rockafellar, R. (1976) Monotone Operators and the Proximal Point Algorithm. SIAM Journal on Control and Optimization, 14, 877-898. http://dx.doi.org/10.1137/0314056
[26]	Bauschke, H.H., Burachik, R.S., Combettes, P.L., Elser, V., Luke, D.R. and Wolkowicz, H. (2011) Fixed-Point Algorithms for Inverse Problems in Science and Engineering. Springer, Berlin. http://dx.doi.org/10.1007/978-1-4419-9569-8
[27]	Combettes, P.L. and Wajs, V.R. (2005) Signal Recovery by Proximal Forward-Backward Splitting. Multiscale Modeling & Simulation, 4, 1168-1200. http://dx.doi.org/10.1137/050626090
[28]	Ochs, P.Y. and Cooper, G. (2014) IPiano: Inertial Proximal Algorithm for Nonconvex Optimization. SIAM Journal on Imaging Sciences, 7, 1388-1419. http://dx.doi.org/10.1137/130942954
[29]	Garroni, M.G. and Menaldi, J.L. (1992) Green Functions for Second-Order Parabolic Integro-Differential Problems. Longman, London.
[30]	Addou, A. and Benbrik, A. (2002) Existence and Uniqueness of Optimal Control for a Distributed-Parameter Bilinear System. Journal of Dynamical Control Systems, 8, 141-152. http://dx.doi.org/10.1023/A:1015372725255
[31]	Fursikov, A.V. (2000) Optimal Control of Distributed Systems. Theory and Applications. American Mathematical Society.
[32]	Ekeland, I. and Témam, R. (1999) Convex Analysis and Variational Problems. SIAM, Philadelphia.
[33]	Gaviraghi, B., Annunziato, M. and Borzì, A. (2015) Analysis of Splitting Methods for Solving a Partial-Integro Fokker-Planck Equation. Applied Mathematics and Computation, 294, 1-17. http://dx.doi.org/10.1016/j.amc.2016.08.050
[34]	Schiesser, W.E. (1991) The Numerical Method of Lines. Academic Press, Pittsburgh.
[35]	Chang, J.S. and Cooper, G. (1970) A Practical Difference Scheme for Fokker-Planck Equations. Journal of Computational Physics, 6, 1-16. http://dx.doi.org/10.1016/0021-9991(70)90001-X
[36]	Mohammadi, M. and Borzì, A. (2015) Analysis of the Chang-Cooper Discretization Scheme for a Class of Fokker-Planck Equations. Journal of Numerical Mathematics, 23, 125-144. http://dx.doi.org/10.1515/jnma-2015-0018
[37]	Strang, G. (1968) On the Construction and Comparison of Difference Schemes. SIAM Journal on Numerical Analysis, 5, 506-517. http://dx.doi.org/10.1137/0705041
[38]	Marchuk, G.I. (1981) Methods of Numerical Mathematics. Springer, Berlin.
[39]	Hundsdorfer, W. and Verwer, J.G. (2010) Numerical Solutions of Time-Dependent Advection-Diffusion-Reaction Equations. Springer, Berlin.
[40]	Geiser, J. (2009) Decomposition Methods for Differential Equations: Theory and Applications. Chapman & Hall, London. http://dx.doi.org/10.1201/9781439810972
[41]	Schindele, A. and Borzì, A. (2016) Proximal Schemes for Parabolic Optimal Control Problems with Sparsity Promoting Cost Functionals. International Journal of Control.