Game Theory Application and Strategic Bidding in Electricity Supply Market ()
1. Introduction
The establishing of electricity pool come with the electricity industry deregulation. Its original aim is to reduce electricity price to the final consumer via introducing competition. As competition introducing, in a deregulated electricity power market, participants are focusing on their own benefit. And the competitive environment enables- market participants to seek to maximize profit via pricing their electricity strategically. This Paper focuses on the study of generators’ behaviors in electricity power supply market. An electricity pool model (EWPP-England and Welsh Power Pool, supply side only) is simulated to explore the competitive behavior of generators. In pool model, electricity trading is centralized, and use merit order dispatch. Generating companies make their bid to Independent system operator (ISO), ISO ranks these bid from lowest price to highest price and arrange the electricity generation according to the demand side offer or load forecast.
In competitive pool model, generating companies could use strategic bidding to seek maximum profit. Game theory as a study of strategic decision making was introduced to analysis the bidding behaviors of generating companies.
To explore the bidding behaviors of generating companies in pool model, a 3 generator bidding game is modeled. In this model, generator companies are regarded as player and these players are in an incomplete information environment, in which each player has full information on itself but lacks other players’ information. All these players are trying to maximize their benefit. Hence this game is a non-cooperative game. Nash Equilibrium has shown excellent performance in the non-cooperativegame. It will be used in our model as a critical method in analysis optimal bidding problem.
2. Market Type and Game Theory Concepts
2.1. Electricity Pool Mode
Trading process in an electricity pool mode is centralized, which means generating plants that participating electricity pools must make bids, be scheduled and be dispatched centrally. Bids of market participants refer to the price of corresponding generation volume, and this price does not have to reflect its marginal cost. The auction in pool mode is a uniform auction. The bidding in our electricity pool model is supply- side only.
2.2. Strategic Bidding
Global social welfare quantizes the total benefit earned in transactions. It is usually used to measure the performance of the market. Here the global social welfare is equal to the sum of profit of generator and the net consumer surplus. It reflects the willingness of society to pay for the electricity. A globe welfare could achieve maximize in a perfect competition market. While the real market is usually not a perfectly competitive market, it has a lower efficiency than a perfectly competitive market and its global welfare positioning in a lower level.
A perfect electricity power market has sufficient amount of power suppliers and consumers. Therefore all these power suppliers are a price taker. In microeconomic theory point of view, the optimal bidding strategy for a supplier in a perfect competitive market is to bid at its short-term marginal cost. Hence, its production should be adjusted to ensure its marginal price equal to the market price. At this time, all market participants are in an equilibrium status. No one could benefit from strategic bidding. Because if the supplier increases its price, it will lose its market share and cannot sell any electricity; on the contrary, if the supplier reduces its price, its price is lower than the marginal price, in this situation, it is not worth to continue producing. However, strategic bidding enables a supplier to make a profit in an imperfect market. Generally, in an imperfect market, there exists at least one supplier that has a certain large market share. The behaviors of this supplier to make a profit via strategic bidding are regard as exertions of market power [1].
In theory, a perfectly competitive market could maximize the global social welfare. Thus it is a desirable market. Although the current market structure and the mecha- nism are sufficiently well designed, perfectly competition still can not be realized.Is is because the natural characteristic of electricity power industry. For example, huge investment costs limit the number of suppliers, transmission losses adverse long distance transmission and transmission constraints restrict the path of power flow. These characteristics enable a few generating companies could oligopoly in a geographic region and exert market power [2]. To exert market power enable to maximize profit, a generator uses optimal bidding strategies. The optimal bidding strategies could achieve in three ways [3].
1) Estimate the Market Clearing Price (MCP): It is the most efficiency way to make optimal bidding strategies if a generating company could accurately estimate the MCP. The generating company just need to set their bidding price a slightly lower than the MCP. Whereas the estimation of MCP cannot be exactly accurate, because the history date is not enough and loads forecast is not reliable due to the fast developing of the electricity industry.
2) Estimate other market participants’ bidding behavior. As the bids of market participants are private and generating companies are not paid according to their bidding prices, there is rare information available to predict other players’ behavior. Cur- rently available methods in this kind of estimation are fuzzy logic and probability analysis.
3) Game Theory methods. Matrix game based method and oligopoly game method. The characteristic of the first one is that it uses discrete quantities as bidding strategies, while the second one based on some classic models, for example, Cournot model and Stackelberg model.
2.3. Game Theory Application to Bidding Transactions
A game can define as a complete information game (c-game) or incomplete information game (i-game). The power transactions in a pool model is a typical incomplete game.Every player has full information of its own payoffs while it does not have full information of other players [4].
Also, a game also can be regard as perfect information game or imperfect information games. If players have full information of the early stage movement, this game is a perfect game. While in an imperfect game, players do not have full information on the early stage movements.
An incomplete information game could transfer to a completed game with imperfect information. Nash Equilibrium idea could apply in the transformed game in order to solve the optimal bidding problem. The optimal bid of each play is their bid in the state of Nash Equilibrium.
2.4. Mathematical Expression of Costs and Profits in Power Transactions
The expression of the cost of generator  is:
is:
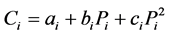 (1)
(1)
The initial state of participant 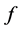 with several generators and total load
with several generators and total load 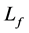 before participating transaction is
before participating transaction is 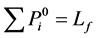 . The marginal cost is derivation of incremental cost again generation changes:
. The marginal cost is derivation of incremental cost again generation changes:
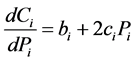 (2)
(2)
Players (participants) make bids as equation 2 to ISO, ISO arrange the dispatch schedule using merit order methods. The price of the minimum bid matching load required is the market spot price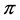 . The scheduled generation for participant
. The scheduled generation for participant  is
is
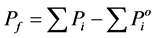 , it represented the sum of efficient output of all units. Here
, it represented the sum of efficient output of all units. Here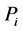 is actual the generation level of generator i.
is actual the generation level of generator i.
The profit of the player f is:
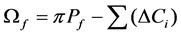 (3)
(3)
To maximize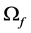 , let the derivation of equation 3 = 0, The player should adjust its generation to make its marginal cost matches:
, let the derivation of equation 3 = 0, The player should adjust its generation to make its marginal cost matches:
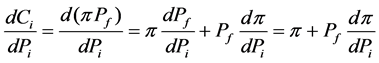 (4)
(4)
In the perfectly competitive market, the market has sufficient buyers and sellers, and none of these participants has an enough large market share. Thus none of them could affect the existing spot price. As shown in equation 4, the optimal bid price for a player in the perfectly competitive market is to bid at the given spot price  via adjusting its production to match its marginal price equal to
via adjusting its production to match its marginal price equal to .
.
While in an imperfect competition, participants could obtain more profit by strategic bidding. Hence the electricity pool is modeled as anon-cooperative game that enables its players purchasing maximum profit via competition.
From Equation (3), the profit of a player depends on the spot price, scheduled generation, and its cost. Due to the spot price and scheduled is not under the direct control of players, the direct way to maximize profit is adjusting its bids. So the strategy of a player is to adjust 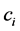 to adjust its bid, that is, a player’s strategies are bid
to adjust its bid, that is, a player’s strategies are bid 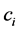 times of its marginal cost [5].
times of its marginal cost [5].
3. Three Generators Bidding Game
The idea of modeling a 3-generator bidding game is to explore players’ bidding behaviors and optimal strategies in a game with multi-players. These threegenerators are simulated to compete against each other in EWPP. Thedata of these generators selected from ESIS. They belong to top three market share generators. The selected three generators are shown in Table 1, while Table 2 shows the data each generator, it represents the short-term marginal cost and generation capacity of every generating unit.
In this game, game players are these 3generators; their strategies are the bids they made to ISO. These bids based on the marginal costs of each unit; they can bid 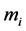
![]()
Table 1. Market share of 3 selected generators.
![]()
Table 2.Generating Units’ Short term marginal cost and generation capacity of each generator.
times of its marginal cost. To simplify this game, all units of a generator use a same bid strategy. Hence the bids of each generator are simple bids rather than complex bids. To avoid huge matrix, we simplify the strategies. In our game, let ![]() equal to 1, 1.5, 2 respectively. That is to say, the strategies set of each player is (1, 1.5, 2) times of its marginal cost.
equal to 1, 1.5, 2 respectively. That is to say, the strategies set of each player is (1, 1.5, 2) times of its marginal cost.
We use [Gen1, Gen2, Gen3] to present players strategy profile. For example, [MC, 2MC, 1.5MC] represent that the strategy of G1 is bidding at its marginal cost, the strategy of G2 is bidding at 2 times of its marginal cost and G3 is bidding at 1.5 times of its marginal cost.
The payoffs of players are the profits of generators. The calculation of generators payoff based on the system marginal price and the electricity it generated. As we discussed before, generators make bids to ISO (uniform auction), ISO schedule and arrange dispatch using merit order method. This method ranks generators bids from lowest to highest and selects the bid matching electricity supply and load demand as the marginal product of the system. The price of this bid is the system marginal price (SMP). It is also known as market clearing price (MCP). In this game, we assume the load demand is 12,000 MW. Figure 1 shows the Merit order dispatch in determining SMP.
3.1. Payoff Matrix
Microsoft Excel was used in simulating merit order algorithm, calculate MCP and each player’s payoff. Table 3 shows an example of how it works.
Table 3 is used to calculate each player’s payoff. The strategy profile is [MC, MC, MC], it means every generator are bids at its marginal cost. Red font color was used to present G1’s units, blue forG2 and green forG3’s units. The bid of a unit is equal to the product to its marginal price and its strategy. Then we sort these bids in ascending
![]()
Table 3.An Excel example of merit order method in determining MCP.
![]()
Figure 1. Merit order despatch in determining SMP.
order and compare the cumulative availability with the load demand, we could find the system marginal product and determine the system marginal price. Also, all the output of unit plant whose bid lower than SMP will be scheduled to dispatch. In this strategy profile, the SMP is 19.9 £/MWh. The payoff [Gen1, Gen2, Gen3] is [58.72, 38.52, 21.47] k£/h.
After finishing similar work of all strategies profile like [MC, MC, MC] in Table 3, we got the payoff matrix of this game. The payoff matrix shows in Table 4. The payoff matrix in Table 4 is a 3-d matrix.
3.2. Optimal Bidding Strategy and Nash Equilibrium
To solve the optimal bidding problem, we introduce the concept of Nash equilibrium in our non-cooperative 3-generator game.
Nash equilibrium is an equilibrium state in a game that each player is playing the best response to others. It means that on one could benefit from changing its own strategy while the others remain their strategies unchanged. So the strategy that each player used in Nash Equilibrium is their optimal strategy.
That is to say, in our game, if three generators are in Nash Equilibrium, none of them could gain a higher profit from changing its own bid while the other two generators remain their bids.
GAMBIT 14 is a software to find Nash Equilibrium. We build a three players game in GAMBIT and input the payoff matrix we got previously. Then use GAMBIT to find the Nash Equilibrium.
As Table 5 shows, the column with yellow background presents the Nash Equili- brium. It reflects the optimal strategy profile is [1MC, 2MC, 1MC], and the payoff for each generator at Nash Equilibrium is [112.19, 40.41, 47.02] k£/h respectively.
This game is an incomplete game at the beginning because each generator only has its own information but lacks others’ information. Moreover, this game is an imperfect
![]()
Table 4.Payoff matrix of different strategies profile including the corresponding SMP.
![]()
Table 5.Nash Equilibrium in the payoff matrix.
game as three generators do not have full information on other player’s moves in early stages. However, as time going on, from the interaction of generators, a generator could estimate other players’ strategy and correspond SMP according to history data. Finally, the incomplete game transform to a complete game with imperfect information. And we could use Nash Equilibrium to determine optimal bidding strategy.
In our model, the optimal bidding strategy for each generator is bidding at 1 MC, 2 MC, 1 MC respectively. As generator 3 is the smallest generator, in most time, it is a price taker, which should better not bid high. G1 and G2 have a similar market share. One bid high will lose dispatch and increase the other’s profit. As G2’s profit caused by high SMP exceed the loss due to increasing bid, G2 could bid high. At the same time, G1 and G3 could benefit from G2’s high bidding. The market in our model is an example of imperfectly competitive market that shows a market participant with a large percentage market share could affect the market price to exert market power. If the market is competitive, more generators with similar market share could participate in the competition, and there will be more choice for ISO. As a result, if one particular market participant increases its bid, ISO could select another generator. Hence, in a competitive market, bid high is unwise, and the competition will push down the prices and increase participants’ efficiency.
Our model bases on the competition on bidding prices and the bid are simple. While in real competition in EWPP, generators not only compete on prices but also compete on outputet al. Also, in areal environment, bids are complex bids. Moreover, generators submit complex units for every unit. These bids reflect the unit’s technique parameters, output level for instance, and cost characteristic, such as marginal cost, start-up cost, no load cost.
4. Conclusions
The behavior of participants in electricity power market is modeled as anon- cooperative game because, in the market, each participant is competing against each other to maximize its own profit. When a generator has a larger market share, its bidding could affect the market price. This bidding behavior defines as an exercise of market power. Though the market designers are trying to realize perfect competition in the electrical market, and no matter how they improve the market mechanism, sometimes market participants could exert market power. It is determined by the inherent characteristic of electricity power market that some generator is inevitable to monopoly in a geographical region. It is the weakness of pool market. Generators could take advantages of the weakness to increase profit via limiting supply and bidding as high as possible.
To mitigate market power, some strategies have been used, such as increase additional capacity and back-up, establish information dissemination mechanism, allowing institutions with small generators enter the market [6]. In addition, to deal with congestion, transmission line should be managed to expand. In some particular condition, set a temporary price cap is necessary. In a word, no matter what methods used to mitigate market power, the basic idea is to guarantee adequate supply.
Moreover, we modeled a 3-generator bidding game to simulate the competition in EWPP. In this game, these generators compete against each other to maximize its own profit. Hence it is a non-cooperative game. Merit order method is used to schedule generation dispatch. Large generators could affect the SMP via different bidding strategies. If two generators have similar market share, one bid high will lose generation while the other would be scheduled to generate more. If the profit from the increased SMP could not compensate the loss from being less dispatched, the best choice for the generator is not to make a higher bid. While in a real market with many generators, ISO have more choice, a particular generator’s high bid could not significantly increase the SMP, hence the generator tends to bid low.
In our model, Nash Equilibrium is used to solve the optimal bidding problem. Because in Nash Equilibrium, every player is playing their best response to the others, hence no one could benefit from its own strategy while others remain their strategy unchanged. So the Nash Equilibrium strategy is the optimal bidding strategy.
However, in real electricity power market, the optimal long-term strategy does not exist. The main reason support this idea is that the real electricity market is expanding very quickly, and the available information is limited, the original incomplete information game could not transfer to a completed game with imperfectly information and Nash Equilibrium could not apply. Thus it can be seen how important of the information system, it allows all generators in a fully competitive market have the opportunity to analysis their opponents’ strategy and adjust their own strategy accordingly.
Acknowledgements
I would like to express my sincerely gratitude to my supervisor Professor K.L. Lo, Head of Power System Research Group, Institute of Energy and Environment of the University of Strathclyde, for his valuable guidance and great help throughout my entire work. Thanks are also expressed to my colleagues, especially Xinwen Ni and Zhonglei Shao, of Power System Research Group at University of Strathclyde for the interesting discussions that doubtless enriched methods worked in this paper.