
Subject Areas: Theoretical Physics

1. Introduction
Mathematically complex wave functions were the first choice of the founders of quantum mechanics. This type of functions is mandatory for the Schroedinger and the Dirac equations, whose form is
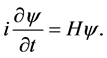 (1)
(1)
Here the Hamiltonian 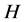 is a Hermitian operator which has real eigenvalues. Furthermore, the equation holds for a massive particle and each side of (1) represents the system’s energy, which means that it takes a real positive value. So, if
is a Hermitian operator which has real eigenvalues. Furthermore, the equation holds for a massive particle and each side of (1) represents the system’s energy, which means that it takes a real positive value. So, if 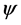 is real then the left hand side of (1) is pure imaginary whereas its right hand side is real. It follows that a real wave function cannot satisfy the Schroedinger and the Dirac equations. For this reason complex wave functions are intensively treated in quantum mechanics textbooks. This feature holds since the very early days of this theory.
is real then the left hand side of (1) is pure imaginary whereas its right hand side is real. It follows that a real wave function cannot satisfy the Schroedinger and the Dirac equations. For this reason complex wave functions are intensively treated in quantum mechanics textbooks. This feature holds since the very early days of this theory.
A different course was taken few years later, when two mathematically real quantum equations were published. The first case was the real version of the Klein-Gordon (KG) equation, which was used in 1935 by Yukawa for a theoretical interpretation of the nuclear force (see e.g. [1] , p. 211). Soon after, Majorana published a pure imaginary version of the Dirac  matrices which cast the Dirac equation into a mathematically real form (see [2] , p. 486).
matrices which cast the Dirac equation into a mathematically real form (see [2] , p. 486).
The quantum equations of Yukawa and of Majorana have a relativistic covariant structure. The same property holds for other real quantum equations, like those of the Higgs and the 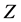 bosons (see e.g. [3] ). For this reason, expressions used in this work take a relativistic covariant form.
bosons (see e.g. [3] ). For this reason, expressions used in this work take a relativistic covariant form.
General considerations are described in the second section. The third section contains a derivation of new problematic issues of mathematically real quantum theories. The last section contains concluding remarks. This work uses standard notation of relativistic expressions. Greek indices run from 0 to 3 and Latin indices run from 1 to 3. The metric is diag (1, −1, −1, −1). Units where 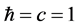 are used.
are used.
2. General Considerations
The quantum theory is about 90 years old. It aims to explain the dual nature of an elementary particle, namely, a pointlike particle that has wave properties. There is a vast literature that discusses many attributes of this theory. On the other hand, quantum effects provide a basis for modern industry which uses transistors, lasers etc.
Quantum theories can be classified as follows:
1) Nonrelativistic quantum mechanics.
2) Relativistic quantum mechanics (RQM).
3) Quantum field theory (QFT).
These theories apply to an increasing order of their domain of validity. Nonrelativistic quantum mechanics holds for nonrelativistic states and processes. RQM holds for cases where the number of particles can be regarded as a constant of the motion. QFT describes processes containing phenomena of particle creation and annihilation.
For example, the nonrelativistic Schroedinger equation explains some properties of the hydrogen atom. The Dirac equation is the corresponding relativistic equation and it provides a much better explanation for the hydrogen atom properties. Tiny effects of creation and annihilation of virtual particles are explained by QFT. These tiny corrections are confirmed by experiments that measure the hydrogen atom properties. A production of particles, like electron-positron pair production, is demonstrated in high energy experiments. This production is explained by QFT.
Evidently, these theories are connected by appropriate limiting processes. Thus, for small velocity (namely, in cases where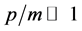 ) RQM goes to nonrelativistic quantum mechanics. Particle creation and annihilation are described by a probabilistic coefficient. In cases where this coefficient is very small, QFT goes to RQM. This chain of relationships connects QFT to nonrelativistic quantum mechanics. This matter is stated loud and clear in S. Weinberg’s QFT textbook (see [4] , p. 49):
) RQM goes to nonrelativistic quantum mechanics. Particle creation and annihilation are described by a probabilistic coefficient. In cases where this coefficient is very small, QFT goes to RQM. This chain of relationships connects QFT to nonrelativistic quantum mechanics. This matter is stated loud and clear in S. Weinberg’s QFT textbook (see [4] , p. 49):
“First, some good news: quantum field theory is based on the same quantum mechanics that was invented by Schroedinger, Heisenberg, Pauli, Born, and others in 1925-1926, and has been used ever since in atomic, molecular, nuclear and condensed matter physics”.
Later on, this assertion is called Weinberg’s QFT correspondence principle (see also [5] , pp. 1-6). Thus, the appropriate limits of RQM and of QFT must agree with fundamental properties of quantum mechanics. There- fore, properties of quantum mechanics make constraints on the acceptability of theories belonging to RQM and to QFT. In the Schroedinger equation, particle density takes the form  (see [6] , p. 22 or [7] , pp. 53-55). Density demonstrates another aspect of the relationships between QFT, RQM and quantum mechanics. Indeed, density is used in the definition of the inner product of the Hilbert space of quantum mechanics and of RQM. This Hilbert space is used for constructing the Fock space of QFT, where particle occupation number is defined. It should be pointed out that the Hilbert space is a fundamental element of quantum mechanics (see [4] , p. 49, item (i)). The problem of defining a self-consistent expression for density plays a key role in the following discussion.
(see [6] , p. 22 or [7] , pp. 53-55). Density demonstrates another aspect of the relationships between QFT, RQM and quantum mechanics. Indeed, density is used in the definition of the inner product of the Hilbert space of quantum mechanics and of RQM. This Hilbert space is used for constructing the Fock space of QFT, where particle occupation number is defined. It should be pointed out that the Hilbert space is a fundamental element of quantum mechanics (see [4] , p. 49, item (i)). The problem of defining a self-consistent expression for density plays a key role in the following discussion.
The analysis relies on basic properties of a quantum particle which are briefly presented in the following lines. The wave nature of such a particle is considered as a primary attribute of a quantum theory. Here the de Broglie formula for the wave length of a massive particle is related to its momentum (see [6] , p. 3 or [7] , pp. 48, 49)
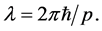 (2)
(2)
For the simplicity of the discussion, let us examine a free massive quantum particle, like an electron in a re- gion of space where external electromagnetic fields vanish. The phase of its wave takes the form
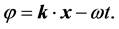 (3)
(3)
The de Broglie relationship means that the particle’s energy and momentum appear as elements of its phase where ( )
)
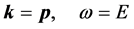 (4)
(4)
It is interesting to note that (3) and (4) prove that the phase 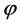 is a Lorentz scalar obtained from the contrac- tion of the energy-momentum 4-vector
is a Lorentz scalar obtained from the contrac- tion of the energy-momentum 4-vector 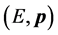 and the space-time coordinates
and the space-time coordinates 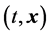 (multiplied by
(multiplied by![]() ). Con- sequently, it takes the same form in nonrelativistic and relativistic quantum theories.
). Con- sequently, it takes the same form in nonrelativistic and relativistic quantum theories.
A quantum theory of a given particle must describe the time evolution of its state. This objective takes the form of a differential equation. Relying on the foregoing expressions, one finds that appropriate differential operators are related to the particle's energy and momentum. These operators take the form
![]() (5)
(5)
These relationships show the connection between dynamical quantities and differential operators.
The following section relies on Weinberg’s QFT correspondence principle and shows how the fundamental quantum issues described above affect the structure of QFT.
3. Mathematically Real Quantum Theories
As stated above, the quantum Equation (1) proves the well known complex form of the Schroedinger and the Dirac wave function. Let us examine the possibility of describing a massive quantum particle by means of a real wave function. A simple case is that of a free particle moving along the positive x-direction. The form of the factor that describes the undulating properties of its wave function can be written as a linear combination of the following expressions (see [6] , p. 18)
![]() (6)
(6)
The last expression of (6) is a complex function which depends on the particle’s energy and momentum. Therefore, it is unsuitable for a real wave function. Evidently, every linear combination of the first and the second functions of (6) can be written in the form![]() , where
, where ![]() is a constant number. Hence, a real wave function of a free massive particle moving along the positive x-direction takes the form
is a constant number. Hence, a real wave function of a free massive particle moving along the positive x-direction takes the form
![]() (7)
(7)
where ![]() is a normalization factor.
is a normalization factor.
The free quantum particle that is analyzed here is massive and it has a rest frame. (It should be noted that the following analysis does not apply to the photon because this particle has no rest frame). In this frame the particle’s linear momentum is ![]() and its wave function (7) reduces to the form
and its wave function (7) reduces to the form
![]() (8)
(8)
It follows that for every integer n, the real wave function (8) vanishes identically throughout the entire 3-dimen- sional space at every instant t when![]() .
.
Evidently, if the wave function vanishes at a certain point then the particle’s probability density vanishes there. This is the basis for the quantum interpretation of an interference pattern. Therefore, the fact that the real wave function vanishes at the entire 3-dimensional space means that at the corresponding instant the particle disappears. Hence, the following results are obtained:
1) A conserved density cannot be consistently defined for a particle described by a mathematically real wave function.
2) The lack of a consistent expression for density means that a Hilbert space of quantum mechanics and its associated Fock space of QFT cannot be constructed.
3) Obviously, due to the absence of these spaces, operators used in mathematically real quantum theories be- come meaningless. Another discrepancy that stems from the missing Hilbert and Fock spaces is that a calcula- tion of transition amplitude between quantum states becomes impossible.
These findings prove the existence of inherent contradictions in quantum theories of a mathematically real wave function. Beside the foregoing specific issues, these theories violate the Weinberg’s QFT correspondence principle, because density is a well defined quantity in the nonrelativistic Schrodinger theory. Note that the proof takes a general form which is independent of the specific structure of any given mathematically real quantum theory. Therefore, it applies to all quantum theories of this kind.
Here the following question arises: Why the Noether theorem does not provide a consistent expression for density of a particle whose quantum equation of motion takes a mathematically real form?
In the case of a Majorana particle the answer depends on the absence of an appropriate eigenfunction. Indeed, the Majorana Lagrangian density is (see [2] , Equation (105))
![]() (9)
(9)
where the four ![]() matrices are pure imaginary. Moreover, like the Dirac equation, the Majorana equation is a first order partial differential equation. For this reason, (7) does not solve the Majorana equation because the first derivative of the
matrices are pure imaginary. Moreover, like the Dirac equation, the Majorana equation is a first order partial differential equation. For this reason, (7) does not solve the Majorana equation because the first derivative of the ![]() function is the
function is the ![]() function. Obviously, the Noether theorem applies only to cases where the function
function. Obviously, the Noether theorem applies only to cases where the function ![]() of the Lagrangian density solves the quantum equation.
of the Lagrangian density solves the quantum equation.
Another argument that disproves the Majorana theory stems from the definition of the following function of (9)
![]() (10)
(10)
(see [1] , p. 24). So if each of the four Majorana ![]() matrices is pure imaginary then the quantum equation
matrices is pure imaginary then the quantum equation
![]() (11)
(11)
is real and so is its solution![]() . However, due to the definition of (10), there is an additional
. However, due to the definition of (10), there is an additional ![]() factor in the Majorana Lagrangian density. Therefore, the following contradictions hold for the Majorana theory.
factor in the Majorana Lagrangian density. Therefore, the following contradictions hold for the Majorana theory.
The Lagrangian density and its action
![]() (12)
(12)
are pure imaginary due to the additional![]() . The same contradiction is found in the Majorana Hamiltonian. Indeed, if the Lagrangian density is pure imaginary then also the associated Hamiltonian is pure imaginary. (The mass term
. The same contradiction is found in the Majorana Hamiltonian. Indeed, if the Lagrangian density is pure imaginary then also the associated Hamiltonian is pure imaginary. (The mass term ![]() of (12) provides a simple illustration of this conclusion. Indeed, if
of (12) provides a simple illustration of this conclusion. Indeed, if ![]() is pure imagi- nary then the mass term is pure imaginary). This is a contradiction, because energy, which is an eigenvalue of the Hamiltonian, is a real quantity.
is pure imagi- nary then the mass term is pure imaginary). This is a contradiction, because energy, which is an eigenvalue of the Hamiltonian, is a real quantity.
The following argument explains the origin of the problem. The Majorana ![]() matrices (see [2] , Equation (12)) satisfy the Dirac condition where
matrices (see [2] , Equation (12)) satisfy the Dirac condition where ![]() is Hermitian and the three
is Hermitian and the three ![]() are anti-Hermitian. Therefore, one expects that the Majorana equation has real eigenvalues for its Hamiltonian. The pure imaginary result which is found above for the Hamiltonian eigenvalues means that eigenvalues of the Majorana Hamiltonian should be zero, because zero is the only number which is real and also pure imaginary. This property is inconsistent with the assumed positive mass of a Majorana particle.
are anti-Hermitian. Therefore, one expects that the Majorana equation has real eigenvalues for its Hamiltonian. The pure imaginary result which is found above for the Hamiltonian eigenvalues means that eigenvalues of the Majorana Hamiltonian should be zero, because zero is the only number which is real and also pure imaginary. This property is inconsistent with the assumed positive mass of a Majorana particle.
A primary attribute of a Majorana particle is that it is identical to its antiparticle (see [8] , p. 24). For this reason, the neutrino, which is a chargeless spin-1/2 particle is regarded as a candidate that satisfies the Majorana equation. The particle-antiparticle identity enables experimental tests of the existence of a Majorana neutrino. The following experimental results show that the neutrino is not a Majorana particle.
One kind of experimental data is the neutrino (![]() ) and the antineutrino (
) and the antineutrino (![]() ) cross section. The data clearly show that
) cross section. The data clearly show that ![]() and
and ![]() have a completely different cross section where the
have a completely different cross section where the ![]() cross section is about one half of that of
cross section is about one half of that of ![]() (see [9] , p. 3, figure 49.1).
(see [9] , p. 3, figure 49.1).
Another kind of experiment is the search for a neutrinoless double ![]() decay, which is an indication that the neutrino is a Majorana particle (see [8] , pp. 202, 203). In spite of a very long and intensive search, there is no confirmation of this effect and the experimental bound is several orders of magnitudes below the theoretical predictions [10] . It means that there is no experimental support for the Majorana theory. As a matter of fact, this issue is still alive and at the time when these lines are written, several experiments are taking data whereas others are planned to be carried out in the future [10] .
decay, which is an indication that the neutrino is a Majorana particle (see [8] , pp. 202, 203). In spite of a very long and intensive search, there is no confirmation of this effect and the experimental bound is several orders of magnitudes below the theoretical predictions [10] . It means that there is no experimental support for the Majorana theory. As a matter of fact, this issue is still alive and at the time when these lines are written, several experiments are taking data whereas others are planned to be carried out in the future [10] .
As far as this work is concerned, the case of a real KG equation is much simpler, because the absence of density and of a conserved 4-current for this quantum field is proved in a textbook (see [11] , p. 42, Equation (12.8)). Thus, it turns out that the real KG theory also violates the Weinberg’s QFT correspondence principle.
At present there is no experimental support for the real KG particle which is used in the Yukawa theory of nuclear force. Thus, the discovery of quarks in the 1960s proves that a ![]() meson is a
meson is a ![]() bound state. Hence, the
bound state. Hence, the ![]() consists of two elementary particles and its wave function takes the form
consists of two elementary particles and its wave function takes the form![]() , where
, where ![]() denote the coordinates of the
denote the coordinates of the ![]() and the
and the![]() , respectively. By contrast, the function of a KG particle depends on a single set of the four space-time coordinates
, respectively. By contrast, the function of a KG particle depends on a single set of the four space-time coordinates![]() . Hence, the
. Hence, the ![]() is not a Yukawa particle. Evidently, the failure of experimental attempts aiming to detect a real KG particle is consistent with the theoretical contra- dictions of this particle which are pointed out above.
is not a Yukawa particle. Evidently, the failure of experimental attempts aiming to detect a real KG particle is consistent with the theoretical contra- dictions of this particle which are pointed out above.
A search of the literature provides an indirect support for the claim that there is no self-consistent expression for density of a mathematically real quantum theory. Indeed, an expression for density and its associated con- served 4-current can be found for the Schroedinger equation (see e.g. [7] , pp. 53, 54) and for the Dirac equation of the electron (see e.g. [12] , p. 56). By contrast, although quantum theories of a mathematically real wave function are known for eight decades, textbooks do not show a self-consistent expression for density of a particle that is described by these theories.
The following pure leptonic decay mode of the ![]() boson pertains to the theoretical problem found above. Here the data show the electron-positron decay mode (see [13] )
boson pertains to the theoretical problem found above. Here the data show the electron-positron decay mode (see [13] )
![]() (13)
(13)
Analogous decay modes exist for the ![]() and the
and the ![]() leptons. Here each of the outgoing particles is an ordinary Dirac particle which has a well defined expression for density. This property enables the experimental analysis that shows the location of the
leptons. Here each of the outgoing particles is an ordinary Dirac particle which has a well defined expression for density. This property enables the experimental analysis that shows the location of the ![]() disintegration event. On the other hand, it is proved above that the
disintegration event. On the other hand, it is proved above that the ![]() boson has no expression for density and that there are instants when its wave function disappears (see the text after (8)). This issue casts serious doubts on the interpretation of the
boson has no expression for density and that there are instants when its wave function disappears (see the text after (8)). This issue casts serious doubts on the interpretation of the ![]() boson by means of a real quantum function. Indeed, it is not clear how a particle that has no expression for density goes to particles that have a consistent expression for density.
boson by means of a real quantum function. Indeed, it is not clear how a particle that has no expression for density goes to particles that have a consistent expression for density.
4. Conclusion
This work analyzes a class of quantum theories whose wave function takes a mathematically real form. It proves that new problems exist with the corresponding parts of presently accepted physical theories. The analysis relies on well documented physical properties of quantum theories that can be found in standard textbooks. The results show contradictions of the Majorana neutrino theory and of the Yukawa theory of the nuclear interactions. Experimental data provide a solid support for these results. Furthermore, serious problems exist with the current theoretical structure of the Z and the Higgs bosons. This outcome calls for a further analysis of the specific results of this work and of their implications.