Mean Square Solutions of Second-Order Random Differential Equations by Using the Differential Transformation Method ()
Received 21 March 2016; accepted 25 April 2016; published 28 April 2016

1. Introduction
The object of this work is to describe how to implement the differential transformation method (DTM) for finding exact and approximate solutions of the second-order random differential equations. To this end, the second-order random differential equations and the concept of the differential transformation method are presented in Section 2. In Section 3, we consider the statistical functions of the mean square solution of the second- order random differential equation. Section 4 is devoted to numerical examples.
2. Differential Transform Method
The differential transform method (DTM) has been used by Zhou [15] . This method is effective to obtain exact and approximate solutions of linear and nonlinear differential equations. To describe the basic ideas of DTM, we consider the second order random differential equation,
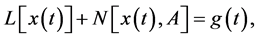 (1)
(1)
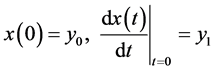 (2)
(2)
where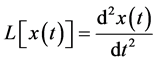 ,
, 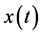 is an unknown function,
is an unknown function, 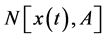 is a nonlinear operator,
is a nonlinear operator, 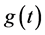 is the
is the
source in homogeneos term, and 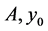 and
and 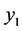 are random variables.
are random variables.
We now write the differential transform of function as
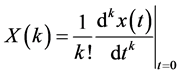 (3)
(3)
In fact, 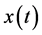 is a differential inverse transform of the form
is a differential inverse transform of the form
 (4)
(4)
It is clear from (3) and (4) that the concept of differential transform is derived from Taylor series expansion. That is
 (5)
(5)
Differential transform for some functions.
Notes that, the derivatives in differential transform method does not evaluate symbolically.
In keeping with Equations (3) and (4), let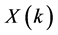 ,
, 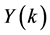 and
and![]() , respectively, are the transformed functions of
, respectively, are the transformed functions of![]() ,
, ![]() and
and![]() . The fundamental mathematical operations of differential transformation are listed in the following table.
. The fundamental mathematical operations of differential transformation are listed in the following table.
3. Statistical Functions of the Mean Square Solution
Before proceeding to find the computation of the main statistical functions of the mean square solution of Equations (1) and (2) we briefly clarify some concept, notation, and results belonging to the so-called ![]() calculus. The reader is referred to the books by Soong [3] , Loeve [16] , and Wong and Hajek [17] . Throughout the paper,
calculus. The reader is referred to the books by Soong [3] , Loeve [16] , and Wong and Hajek [17] . Throughout the paper,
we deal with the triplet Probabilistic space![]() . Thus, suppose
. Thus, suppose ![]() is the set of second
is the set of second
order random variables. Then the random variable![]() , if
, if![]() , where
, where ![]() is an expectation operator. The norm on is denoted by
is an expectation operator. The norm on is denoted by![]() . For example, for the random variable X we define
. For example, for the random variable X we define
![]() , in such way that
, in such way that ![]() is a Banach space. In addition, let T (real interval) represent
is a Banach space. In addition, let T (real interval) represent
the space of times, we say that ![]() is a second order stochastic process, if the random variable
is a second order stochastic process, if the random variable ![]() for each
for each![]() .
.
A sequence of second order random variables ![]() converges to
converges to![]() , if
, if ![]()
To proceed from (4), we truncate the expansion of at the term as follows
![]() (6)
(6)
By using the independence between ![]() and
and ![]() we have
we have
![]() (7)
(7)
![]() (8)
(8)
where ![]()
The following Lemma guarantee the convergent of the sequence ![]() to
to ![]() and the sequence
and the sequence![]() to
to ![]() if the sequence the
if the sequence the ![]() converges to
converges to![]() .
.
Lemma [5] : Let ![]() and
and ![]() be two sequences of 2-r.vs X and Y, respectively, i.e.,
be two sequences of 2-r.vs X and Y, respectively, i.e., ![]() and
and
![]() then
then![]() . If
. If![]() , then
, then![]() ,
, ![]()
and![]() .
.
4. Numerical Examples
In this section, we adopt several examples to illustrate the using of differential transform method for approximating the mean and the variance.
Example 1: Consider random initial value problem![]() ,
, ![]() and
and ![]()
where ![]() and independently of the initial conditions
and independently of the initial conditions ![]() and
and ![]() which satisfy
which satisfy![]() ,
, ![]() ,
, ![]() ,
, ![]() and
and![]() .
.
The approximate mean and variance are
![]()
![]()
Figure 1 explain the Graph of the expectation approximation solution by using DTM with n = 18, while Figure 2 explain the Graph of variance approximation solution by using DTM with n = 18.
Example 2: Consider random initial value problem![]() ,
, ![]() and
and ![]() where A is a Beta r.v. with parameters
where A is a Beta r.v. with parameters ![]() and
and![]() , i.e.
, i.e. ![]() and the initial conditions
and the initial conditions ![]() and
and ![]() are independent r.v.’s such as
are independent r.v.’s such as![]() ,
, ![]() ,
, ![]() ,
,![]() .
.
The approximate mean and variance are
![]()
![]()
Figure 3 explain the Graph of the expectation approximation solution by using DTM with n = 18, while Figure 4 explain the Graph of variance approximation solution by using DTM with n = 18.
Example 3: Consider the problem![]() ,
, ![]() and
and ![]() whereA is a Beta r.v. with parameters
whereA is a Beta r.v. with parameters ![]() and
and![]() , i.e.
, i.e. ![]() and independently of the initial conditions
and independently of the initial conditions ![]() and
and ![]() which are independent r.v.’ satisfy
which are independent r.v.’ satisfy![]() ,
, ![]() ,
, ![]() ,
,![]() .
.
The approximate mean and variance are
![]()
![]()
Figure 1. Graphs of the expectation approximation solution of the DTM with n = 18.
![]()
Figure 2. Graphs of variance approximation solution of the DTM with n = 18.
![]()
Figure 3. Graphs of the expectation approximation solution of the DTM with n = 18.
![]()
![]()
Figure 4. Graphs of variance approximation solution of the DTM with n = 18.
Figure 5 explain the Graph of the expectation approximation solution by using DTM with n = 18, while Figure 6 explain the Graph of variance approximation solution by using DTM with n = 18.
Example 4: Consider the problem![]() ,
, ![]() and
and ![]() where A is a
where A is a
uniform r.v. with parameters ![]() and
and![]() , i.e.
, i.e. ![]() and independently of the initial conditions
and independently of the initial conditions ![]() and
and ![]() which are independent r.v.’s satisfy
which are independent r.v.’s satisfy![]() ,
, ![]() ,
, ![]() ,
,![]() .
.
The approximate mean and variance are
![]()
![]()
Figure 7 explain the Graph of the expectation approximation solution by using DTM with n = 18, while Figure 8 explain the Graph of variance approximation solution by using DTM with n = 18.
Example 5: Consider the problem![]() ,
, ![]() and
and ![]() where A is auniform r.v. with parameters
where A is auniform r.v. with parameters ![]() and
and![]() , i.e.
, i.e. ![]() and independently of the initial conditions
and independently of the initial conditions ![]() and
and ![]() which are independent r.v.’s satisfy
which are independent r.v.’s satisfy![]() ,
, ![]() ,
, ![]() ,
,![]() .
.
The approximate mean and variance are
![]()
![]()
Figure 9 explain the Graph of the expectation approximation solution by using DTM with n = 18, while Figure 10 explain the Graph of variance approximation solution by using DTM with n = 18.
![]()
Figure 5. Graphs of the expectation approximation solution of the HAM with n = 18.
![]()
Figure 6. Graphs of variance approximation solution of the HAM with n = 18.
Example 6: Consider the problem![]() ,
, ![]() and
and ![]() where
where
A is a uniform r.v. with parameters ![]() and
and![]() , i.e.
, i.e. ![]() and independently of the
and independently of the
![]()
Figure 7. Graphs of the expectation approximation solution of the DTM with n = 18.
![]()
Figure 8. Graphs of variance approximation solution of the DTM with n = 18.
initial conditions ![]() and
and ![]() which satisfy
which satisfy![]() ,
, ![]() ,
, ![]() ,
, ![]() and
and![]() .
.
The approximate mean and variance are
![]()
Figure 9. Graphs of the expectation approximation solution of the DTM with n = 18.
![]()
Figure 10. Graphs of variance approximation solution of the DTM with n = 18.
![]()
![]()
Figure 11 explain the Graph of the expectation approximation solution by using DTM with n = 18, while Figure 12 explain the Graph of variance approximation solution by using DTM with n = 18.5.
ConclusionIn this paper, we successfully applied the differential transform method to solve the second-order random
![]()
Figure 11. Graphs of the expectation approximation solution of the DTM with n = 18.
![]()
Figure 12. Graphs of variance approximation solution of the DTM with n = 18.
differential Equations (1)-(2) with coefficients which depend on a random variable A which has been assumed to be independent of the random initial conditions ![]() and
and![]() . This includes the computation of approximations of the mean and variance functions to the random solution. These approximations not only agree but also improve those provided by the Adomian Decomposition Method [12] , Variational Iteration Method [13] and Homotopy Perturbation Method [14] as we have illustrated through different examples. Otherwise, the differential transform method is very effective and powerful tools for the second-order random differential equation because it is a direct way without using linearization, perturbation or restrictive assumptions.
. This includes the computation of approximations of the mean and variance functions to the random solution. These approximations not only agree but also improve those provided by the Adomian Decomposition Method [12] , Variational Iteration Method [13] and Homotopy Perturbation Method [14] as we have illustrated through different examples. Otherwise, the differential transform method is very effective and powerful tools for the second-order random differential equation because it is a direct way without using linearization, perturbation or restrictive assumptions.