Bearing Capacity of Embedded Strip Footing on Geogrid-Reinforced Fly Ash ()
Received 23 February 2016; accepted 27 March 2016; published 30 March 2016

1. Introduction
Coal burning electric utilities annually produce million tons of fly ash as a waste byproduct and the environmentally acceptable disposal of this material has become an increasing concern. In order to reduce the effects of extraneous sources on the environment, it is necessary to increase the proper use and so become a resource rather than undesirable waste material. One of the most promising approaches in this area is use of fly ash as a replacement to the conventional earth material as structural fill material in geotechnical application which will offer several advantages. Fly ash being non-plastic will also solve the problem of dimensional instability as exhibited by plastic soils. The pozzolanic hardening of fly ash imparts additional strength and very few settlements, making it more suitable for use in embankments [1] . Studies on bearing capacity of shallow foundation on a level fly ash ground have been reported by few researchers [2] - [4] . In order to increase bearing capacity of filling material use of reinforcements is a good alternative to other conventional methods of stabilization. The investigations on reinforced fill have demonstrated that both the ultimate bearing capacity and settlement characteristics of the foundation can be improved by the inclusion of reinforcements within the fill. One of the possible solutions to improve the bearing capacity would be to reinforce the sloped fill with the layers of geogrid.
In reality, there are many situations where foundations need to be located either on the top of a slope or on the slope itself. Establishing the bearing capacity of shallow foundations has long been an important component of geotechnical engineering practice. Prandtl [5] sought to establish the punching failure mechanism for thick metals based on the theory of plasticity. The same theory has been evolved to evaluate the bearing capacity of shallow foundations by Terzaghi [6] in which the effects of soil internal angle of friction, soil cohesion, and surcharge were superposed, resulting in the commonly used bearing capacity factors (Nc, Nγ, and Nq). Meyerhof [7] - [10] extended and refined Terzaghi’s theory to better account for the soil strength, footing size and shape, embedment ratio, and slope while assuming a slightly different failure mechanism than that used by Terzaghi and Prandtl. Vesic [11] further expanded on the effects of shallow foundation shape and soil compressibility on ultimate bearing capacity. There has been limited insight into the bearing capacity of footings adjacent to slopes made of fly ash.
Few studies [12] - [18] on bearing capacity behaviour of strip footings on a reinforced slope are reported in the literature where the investigations were conducted with granular soil having single slope angle ranging from 20˚ to 35˚. However, there is very limited information on the integrity, deformation and bearing capacity behaviour of reinforced fly ash slopes when subjected to a vertical load applied to a strip footing positioned close to the slope crest [19] . Therefore reinforced fly ash sloped fill is one of the possible promising areas for bulk utilization of fly ash in geotechnical applications where the fly ash will provide the bulk of the mass in the fill and the reinforcement may provide the necessary strength to the mass of the geotechnical system and if found effective, can provide an economically viable solution particularly for the road and railway embankments. But prior to prototype use it is essential to establish at least experimentally the influence of reinforcement in enhancing the behaviour of footing located near the crest of a fly ash sloped fill. In view of the limited information available on the aforementioned problem, the present investigation aims at the comprehensive investigation relating to the behavior of a loaded strip footing resting on the top of a reinforced fly ash embankment. The aim of present investigation is to find out the efficacy of a single geogrid layer in terms of footing location and depth of embedment when incorporated within the body of a reinforced model fly-ash embankment and loaded at its top surface through the footing. The constant parameters selected for investigation include 45˚ slope angle (β) and single layer geogrid reinforcement of length (Lr = 7B) at 0.30 embedment ratio (Z/B) and the variable is footing location from slope crest; De = 1B, 2B, 3B where B is the width of the footing. These series of tests were performed to investigate the influence of geogrid reinforcement on ultimate bearing capacity and to study the critical location of the footing from slope crest (De).
2. Laboratory Model Tests
2.1. Materials
The fly ash procured from Eklahare Thermal Power Plant, Nashik, Maharashtra, India was used throughout the investigation. The geotechnical properties of fly ash were tested in the laboratories [20] and are shown in Table 1.
The normal ranges of chemical composition of Indian fly ash are given in Table 2. Similarly, the values as suggested by ASTM standards [21] are also given in the table. Further, the chemical composition of the fly ash used in the present investigation was tested in accordance with the Indian Standards [22] . The values obtained after testing corroborates that the said fly ash is class-F fly ash. In the present investigation, instead of prototype
![]()
Table 1. Geotechnical properties of fly ash.
![]()
Table 2. Chemical composition of fly ash.
geogrids, it was decided to use commercially available 1 mm thick polymeric coated polyester geogrid (PET), which is known as the model geogrid. Model geogrid having dimensions of 35 mm × 63 mm was clamped between two roller grips of length and width strip tensile test apparatus in machine direction and cross machine direction respectively. Tensile strength of the model geogrid was 34.60 kN/m at 12.5% and 32.80 kN/m at 11.72% strain, respectively.
2.2. Model Test Tank with Loading Frame
The model tests were conducted in an open ended model test box (Figure 1) having inside dimensions of 2400 mm × 310 mm in plan and 900 mm in depth with a loading frame holding hydraulic jack. The size of the model tank was decided by the size of the footing and the zone of influence. The tank was built sufficiently rigid to maintain plain strain condition. The columns were firmly fixed with six horizontal steel beams; lower beams were firmly clamped in the laboratory ground using eight pins and upper beams were welded with columns.
With the sliding and fixing the position of hydraulic jack on loading frame the roller adapter aligned longitudinally on the model footing. The proving ring was connected to the hydraulic jack with the mild steel extension rod. To achieve this, a roller adapter with 80 mm length and 70 mm diameter was attached with proving ring base for load application on model footing. The maximum capacity 30 kN proving ring was calibrated and attached to hydraulic jack on loading frame with the height adjustment attachment. The loading frame base so designed was fabricated and fixed in the laboratory with concrete. Three sides of the model tank were covered with 12 mm thick transparent Perspex acrylic sheet and supported directly on 8 mm thick mild steel plates and angle columns with nut bolt connections (Figure 2) so that the observer could visualize the failure of the embankment.
2.3. Preparation of Fly Ash Slopes
An experimental program was carried out to study the behaviour of axially loaded model strip footing resting on compacted fly ash slope in plane strain condition. The inner faces of the tank were covered with lubricant to avoid friction between the acrylic sheet and the fly ash. The outer sides of these sheets were marked at 180 - 150
![]()
Figure 1. A line sketch of model test tank.
mm intervals to facilitate accurate preparation of the fly ash slope in layers. The model fly ash fill slope made with a height of 750 mm were compacted in five layers with the horizontal level observed through the Perspex acrylic sheet from both the sides. The fly ash was uniformly mixed with 20% OMC. Each layer was filled for 180 mm and manually compacted for 150 mm with 30 turns of the 60 kg roller compactor. Great care was exercised to level the top surface using special rulers so that the relative density of the top surface would not be affected. After compaction of each layer, the upper surface of fill is roughened with trowel to have good bond between consecutive layers. The preparation of the fly ash fill slope was continued in five layers up to the required level 750 mm form ground. The compacted fly ash bed was cut to desired slope with the help of a sharp edged trowel. When the entire compaction was over, the compacted fly ash slope was covered with wet gunny bags for 22 hours to avoid moisture loss from the slope fill and to ensure uniform moisture distribution throughout the test. In case of reinforced fly ash slope, the reinforcement was placed at the desired depth within the fill (single layer) and the compaction was then continued in a similar manner until the desired height was reached. The length of reinforcement (Lr) was kept constant (7B) throughout the test programme and at any given position the location of the reinforcement was such that it extended up to the face of the slope.
2.4. Strip Model Footing
A Sal wooden strip model footing of size 300 mm length, 100 mm width and 100 mm depth was used with rough base by fixing a thin layer of sand on the base of the model footing with epoxy glue. The footing was positioned on the fly ash fill with the length of the footing running the full width of the tank. The length of the footing was made almost equal to the width of the tank to maintain plane strain conditions. The two ends of the footing plate were polished smooth to minimize the end friction effects. The footing was placed on the surface of the fly ash bed and the axial load was applied on it by a hand-operated hydraulic jack and longitudinally aligned roller adapter with proving ring. The loading frame with sliding arrangement facilitated several edge distances for application of load directly on the footing along length of tank. The load transferred to the footing was measured by a pre-calibrated proving ring attached to the hydraulic jack. The load was applied in increments till failure. The settlement of the footing was measured by two dial gauges with 0.01 mm least count placed on the footing ends.
3. Experimental Procedures
After 22 hours the gunny bags were removed and the planned slope were cut with the sharp trowel, i.e., β = 45˚, then the upper surface is made plane and perfectly horizontal before placing the rough based model footing at planned parametric position location i.e. De = 1B, 2B, 3B from the slope crest. Two magnetic based dial gauges of 0.01 mm least count were placed on the model footing ends to observe the settlements of footing till failure. Initial readings of proving ring were made zero and the initial observations of the two dial gauges were noted; and then each load increment was maintained constant till the footing settlement got stabilized. The roller adapter with proving ring is lowered and oriented axially just above the model footing with the help of oil pumped hydraulic jack operation. The load was applied very slowly at uniform rate (1 mm per minute) so that the footing settlements in the fill were stabilized at a constant rate of strain. Each load increment was maintained constant until the footing settlement had stabilized, around for 5 - 10 minutes. The observations on proving ring and dial gauges were recorded for a fixed interval of loading. The settlement of the footing was measured using two 50 mm travel dial gauges with an accuracy of 0.01 mm placed on opposite sides of the footing ends. From the observations of the tests, finally pressure-settlement curve was drawn and the ultimate bearing capacity of the footing was obtained by using double tangent method [23] . The tests were repeated in order to achieve some degree of confidence with a limit of repeatability ±10% in the ultimate bearing capacity. In case of reinforced fly ash slope, the reinforcement was placed at the desired depth within the fill (single layer) and the compaction was then continued in a similar manner until the desired height was reached. The length of reinforcement (Lr) was kept constant (7B) throughout the test programme and at any given position the location of the reinforcement was such that it extended up to the face of the slope.
4. Results and Discussion
Since the primary objective of the experimental investigation is to evaluate the efficiency of geogrid reinforcement in improving the load carrying capacity of pozzolonic waste material such as fly ash slopes; it is convenient to present the results of the reinforced system with respect to the corresponding results derived for the footing on an unreinforced slope. Initially the tests were conducted with model footings (B = 100 mm) placed on the top of an unreinforced fly ash slope at three different edge distance (De = 1B, 2B and 3B) from the slope crest, 45˚ as the critical slope angle which considered in this investigation. For reinforced slope, the efficiency of a single geogrid layer of length (Lr =7B) was imbedded at its depth of embedment (Z/B = 0.3) at different edge distances (De =1B, 2B, 3B) from slope crest. The results for three different edge distances are compared for unreinforced and single layer reinforced slope (Table 3). To know the pressure-settlement characteristics, the test were conducted on different footing locations, i.e., edge distance (De) from slope crest and the observations were recorded to deduce the pressure settlement (q − δ) curves. Since the pressure-settlement ratio curves do not exhibit a definite failure point, the ultimate bearing pressure of the footing in all the cases is obtained from the pressure-settlement ratio (q − δ) graph by using double tangent method [23] . The footing settlement (w) was ex-
pressed in terms of the footing width (B) as the settlement ratio 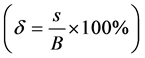 which is the non-dimensional
which is the non-dimensional
parameter. The experimental ultimate bearing capacity values obtained from the model tests of unreinforced and reinforced fly ash slope for various cases have been compared. Using double tangent approach, i.e., crossing points of tangents of two sides of curves, the ultimate bearing capacity for unreinforced slope (qu) and for reinforced slope (qR) with the settlement (δ) was found out. The ultimate bearing capacity for fly ash unreinforced slope (qu) and reinforced slope (qR) used here was taken as the tangent intersection between the initial stiff, straighter portion of the pressure-settlement curve and the steeper, straight portion of the curve as shown in Figure 3.
![]()
Figure 3. Pressure settlement characteristics (β = 45˚).
The comparison of ultimate bearing capacity of unreinforced and reinforced fly ash slope for different edge distances is given in Table 3 and Figure 3. It is seen that with the increasing edge distances, the ultimate bearing capacity is found to increase in the investigation. Notwithstanding, from the results it can be concluded that the effect of edge distance on the bearing capacity is more significant when the footing is located nearer to the crest, i.e., De = 1B or less; but this starts diminishing as the edge distance increases to 2B or 3B for both series of unreinforced and reinforced slope. This change in bearing capacity of footing with its location relative to the slope crest can be attributed to the passive soil resistance from the slope side. When the footing is placed at sufficient distance away from the slope crest, the passive resistance from the slope side to failure wedge under the footing increases and it eventually increases the bearing capacity load. This confirms the significant increase in the bearing capacity of the footing with the increase of footing location distance De from slope crest and decrease of slope inclination.
Further, the results obtained in the present investigation with respect to the ultimate bearing capacity with inclusion of single layer geogrid reinforcement is found increasing when compared with similar parameters of unreinforced slope. The values mentioned in Table 3 indicate that the increasing trend of the bearing capacity is obtained with the inclusion of single geogrid reinforcement. The bearing capacity improvement of footing on reinforced slope is also represented by non-dimensional parameters called bearing capacity ratio (BCR). Bearing capacity ratio (BCR =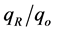 ) is defined as the ratio of the footing ultimate pressure for reinforced slope (qR) to the footing ultimate pressure for the corresponding unreinforced slope (qo). It is being observed that, the bearing capacity ratio (BCR) decreases with edge distance (De) increase from slope crest (Figure 4). In this series all the tests were performed on 100 mm wide footing placed at different edge distances; De = 1.0B, 2.0B, 3.0B from the slope crest at slope angle; β = 45˚. These results are highly consistent with the results reported by some of the researchers [5] [7] [9] [10] for reinforced sand slope, Das et al. [24] for level sand ground though the fill material used in the present investigation is different. Also, the trend of the results is similar to that observed in the available literature [25] .
) is defined as the ratio of the footing ultimate pressure for reinforced slope (qR) to the footing ultimate pressure for the corresponding unreinforced slope (qo). It is being observed that, the bearing capacity ratio (BCR) decreases with edge distance (De) increase from slope crest (Figure 4). In this series all the tests were performed on 100 mm wide footing placed at different edge distances; De = 1.0B, 2.0B, 3.0B from the slope crest at slope angle; β = 45˚. These results are highly consistent with the results reported by some of the researchers [5] [7] [9] [10] for reinforced sand slope, Das et al. [24] for level sand ground though the fill material used in the present investigation is different. Also, the trend of the results is similar to that observed in the available literature [25] .
![]()
Table 3. Experimental values of the bearing capacity (qu) of unreinforced and reinforced fly ash slope (β = 45˚ and Z/B = 0.30).
![]()
Figure 4. BCR―edge distances on single reinforced fly ash slopes (β = 45˚).
The ultimate bearing capacity and the corresponding settlement ratio for the unreinforced case are 55 kPa and 5.50, respectively which increases to 60 kPa and 5.8 when single geogrid reinforcement layer is incorporated in fly ash fill at embedment ratio 0.3. Therefore, it can be concluded that in cases where the excessive settlement is the controlling factor in determining the allowable bearing capacity, incorporation of geogrid reinforcement layer in fly ash fill may significantly decrease the settlement ratio for the same level of bearing pressure.
From Table 3, it can be observed that in general ultimate bearing capacity of footing increases with the increasing edge distance from the slope crest for all the slopes considered in the present investigation. Typical variation of BCR with respect to edge distance for the optimum conditions of single as well as unit edge distance has been presented in Figure 4. This change in bearing capacity of footing with its location relative to the slope crest can be attributed to soil passive resistance from the slope side. If the footing is placed at sufficient distance away from the slope crest, the passive resistance from the slope side to failure wedge under the footing increases.
5. Summary and Conclusions
The bearing capacity behavior of a strip footing resting on the top of a reinforced fly ash slope was investigated experimentally. Results obtained from the present investigation are highly consistent with the previous results reported in literature. Following conclusions may be drawn from the present investigation:
・ Fly ash can be successfully used in geotechnical applications as an embankment fill material as it is standing without fail at slopes steeper than the angle of internal friction of fly ash with or without reinforcement.
・ With increase in slope angle, the bearing capacity decreases for both unreinforced and reinforced slope cases.
・ The load carrying capacity of the footing resting on top of a fly ash slope is greater than the internal angle of friction.
・ Insertion of a geogrid reinforcement layer at suitable location within the sloped fill considerably improves the load carrying capacity of footings located on such slopes.
・ The edge distance has an important bearing on the load carrying capacity of slopes and bearing capacity increases with increase in edge distance. The increasing edge distance of footing on unreinforced and single geogrid layered slope improves the load carrying capacity.
・ Irrespective of the edge distance from slope crest, the bearing capacity ratio (BCR) increases with inclusion of single layered reinforcement.
・ The change in bearing capacity of footing with its location relative to the slope crest can be attributed to passive resistance from the slope side in case of unreinforced slope.
・ Further tests with more embedment depths with single reinforced and multi-reinforced waste fill with more variables and edge distances are recommended.
Acknowledgements
The authors acknowledge the financial support provided by the Savitribai Phule Pune University (SPPU) under the research scheme of Board of University Colleges and Development (BCUD).