Numerical Modeling of Explosive Loading on Strong Rock Mass with Discontinuity System in Depth 25 m ()
Received 11 December 2015; accepted 4 March 2016; published 7 March 2016

1. Introduction
Today, Passive Defense is an important case in army. Passive defense is a civil defense and refers to a series of steps to use weapons do not need to run it possible financial damage to equipment and facilities critical military and civilian casualties or the extent of the damage and prevent losses may be reduced to a minimum. One of the most important principles of Passive Defense is to construct safe structures. Some places such as unity tunnels, underground hospitals and mines can be used as the safe structures for Passive Defense. It is necessary to study on these places and estimate their stability. On the one hand, explosion waves have caused dynamical stress on rock masses around the underground places and led to failure and convergence and new forms around the rock mass that it can be covered stability of underground spaces. Then, it is necessary to study on explosion and its effects on underground structures and stability of these places from explosive loads.
The most important aims of this paper include: study on the important factors in seismic loading effect on stability of underground structures, effect of depth on the rocks with discontinuity system and analyze tunnel stability and amount of wave damping. Generally, stability of these structures against explosive loads from bombs and rockets should be studied before using them as the passive defense structures. On the one side, destroying from rocks and bomb is one of the most complex mechanical processes that it has been studied carefully during 2 centuries ago. At present, three methods can be used to evaluate these cases: finding experimental relations on the basis of repeated tests, developing simple dynamic splash methods, penetration and explosion by using laws of motion and materials and advanced numerical methods to model explosion load effects on underground structures. Methods based on experimental relations are very expensive and especial for each property. Then, they cannot be used for all conditions. Methods based on engineering models are simple with some information. They are ideal to evaluate and study on results from explosion loads. But they are not precise to analyze because of using making simple hypothesizes.
On the other side, advanced numerical methods have considered all cases and provided better results. There are some problems to use numerical methods such as need to precise input information, time to compute, high computational cost, precisely understanding solutions of problem. Because of increasing computational power of computers and saving basic information, researchers and scientists would like to use numerical methods recently.
An explosion is a rapid increase in volume and release of energy in an extreme manner, usually with the generation of high temperatures. TNT is an explosive material and it is stable and pure chemically and it can be compared with various explosive materials [1] . As mentioned above, an explosion is a rapid increase in volume and release of energy in an extreme manner. Based upon it, explosive materials have various explosive specifications regarding type and methods of combination. It consists of:
Released energy, fast explosion that fast explosion of TNT is about 2000 f/s.
There are many important variables that effect on exploring rocks such as properties of stone and explosive materials and explosive patterns. Each explosion has two parameters: Pressure and Volume. Two parameters of distributing different components of energy in explosion process are shown in Figure 1.
On the basis place of exploring to the earth, Explosions can be categorized in three groups [2] :
Explosions that placed up to the earth.
Explosions that placed on the earth (model of this paper).
Explosions that placed under the earth.
2. Background
Sheng-tian and Zhi-yuan (1993) have described dynamic interaction of underground structures and local rocks by using Bending Equations of thick and thin plates [3] . Also, Chen and Zhao (1998) have studied on wave propagation process from explosion in discontinuous and jointed rock masses by using UDEC and AUTODYN [4] . Morris et al. 2004 have presented results from loading of tunnels placed on Nevada Site (they are placed in granite and tuff areas with maximum stresses) by using method of three dimensional separated elements [5] . Lu (2005) has studied on effect of different parameters including geological conditions and density of explosive material on explosion in Swedish tunnels and modeled these results by using Artificial Neural Network [6] . Heuze and Morrise (2006) have performed laboratory and desert tests to model effect of explosion in jointed rock mass [7] . Jiao et al. (2007) has studied on effect of wave propagation from explosion by using Discontinuous Deformation Analysis (DDA) in jointed rock mass [8] . Mortazavi (2003) has evaluated role of strength properties of discontinuities on stability of underground spaces under dynamic load by using Discontinuous Deformation Analysis [9] . Also, Mirzeynali and Bejarivalam (2011) have studied on numerical modeling of explosive loading on weak continuous rock mass by using Finite Difference Method with FLAC (A 2 Dimentional
![]()
Figure 1. Computing explosion wave parameters [11] .
Software) [10] .
3. Method of Computing Explosion Wave Parameters
Today, both experimental and numerical methods can be used to compute wave parameters. In this paper, we use experimental methods and UFC Instruction [11] .
According to UFC Instruction, Figure 1 should be used to compute wave parameters.
where
W: weight of explosive material (on the basis of pond (Ib)).
P: Pressure from explosion (on the basis of PSI).
R: Distance from explosion place (on the basis of ft.).
T: Time (on the basis of ms).
4. Modeling
This rock mass is very strong (RMR > 90). Complete Mechanical Specifications of joints and the rocks have been studied in Table 1 [2] .
4.1. Computing Wave Parameters from Explosion
Both experimental and numerical methods have been used to compute wave specifications from exploring 10 tons TNT.
Based upon it, necessary specifications to find wave coefficients are as follow as:
Distance from Explosion Place (R): place of measuring wave parameters has been placed at a distance of 1.5 m from explosive material, then
 (1)
(1)
Weight of Explosive Material (W): 10 tons TNT.
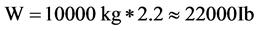 (2)
(2)
Then, Parameter Z will be computed to be used UFC Instruction that is equal to:
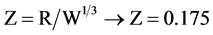 (3)
(3)
At the next stage, pressure from explosion is about psi13250 that is equal to 90.1 as following:
 (4)
(4)
Finally, refer to UFC Instruction (Figure 1) to compute Parameters of Explosive Wave.
4.2. Tunnel Modeling by UDEC
Parameters from explosion wave have been modeled in a tunnel, 25 m in depth. Then, Tunnel Stability will be studied in this depth. After primary modeling in UDEC, the drawn model will be solved because unbalancing powers should be zero (Figure 2).
After wave damping from explosion, developing plastic area, displacement cantores and speed variations are according to Figures 3-5.
![]()
Table 1. Mechanical specifications of rock mass and joints to model [2] .
![]()
Figure 2. Variations of unbalancing powers in the model.
![]()
Figure 3. Developing a plastic area in a tunnel (depth: 25).
![]()
Figure 4. Displacement cantors variations in a tunnel (depth: 25).
![]()
Figure 5. Cantors variations in a tunnel (depth: 25).
Stress changes of the explosion in the ceiling, walls and floor of the tunnel is in accordance with the images below.

Following graph shows displacement variations (vertical and horizontal) in ceiling, walls and floor of tunnel, respectively.

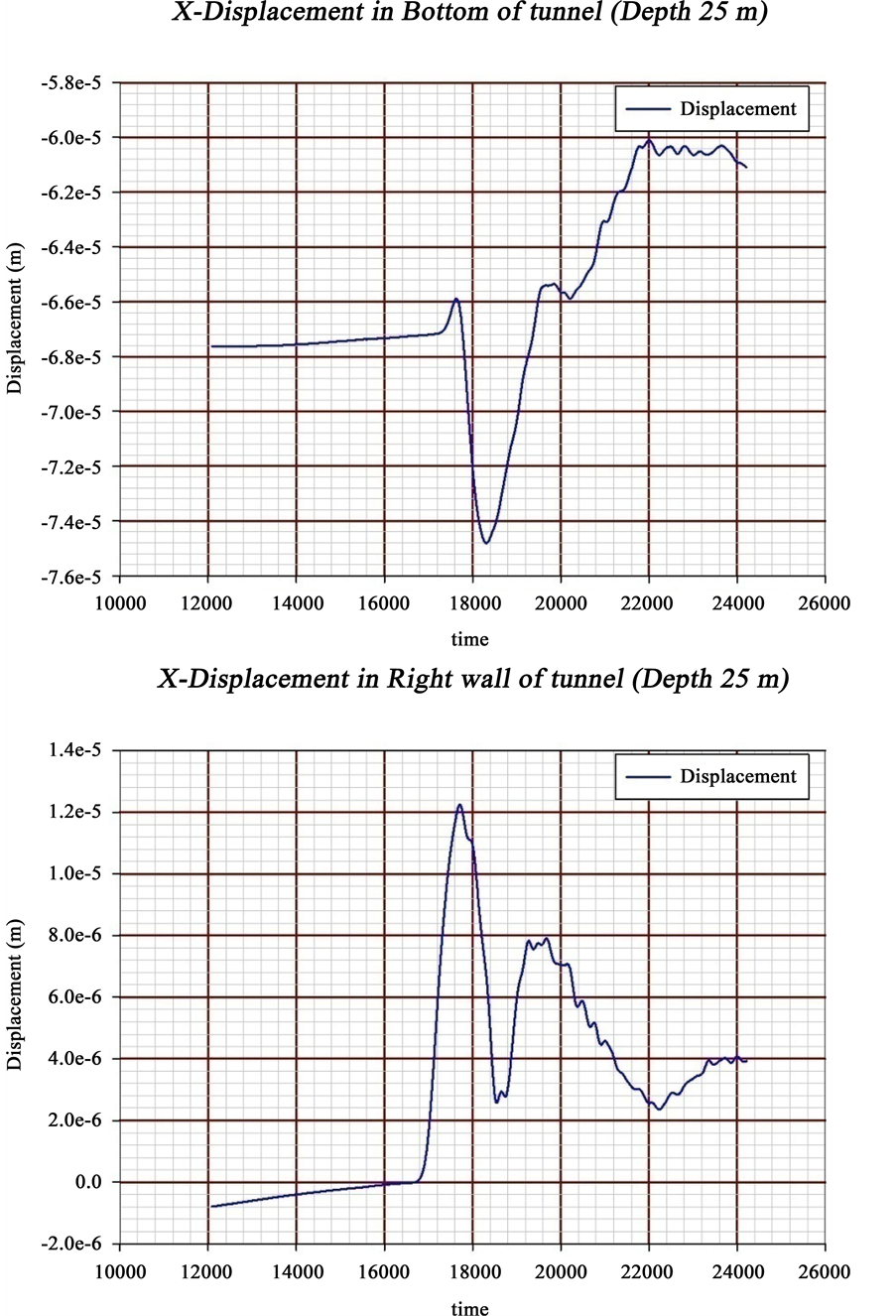
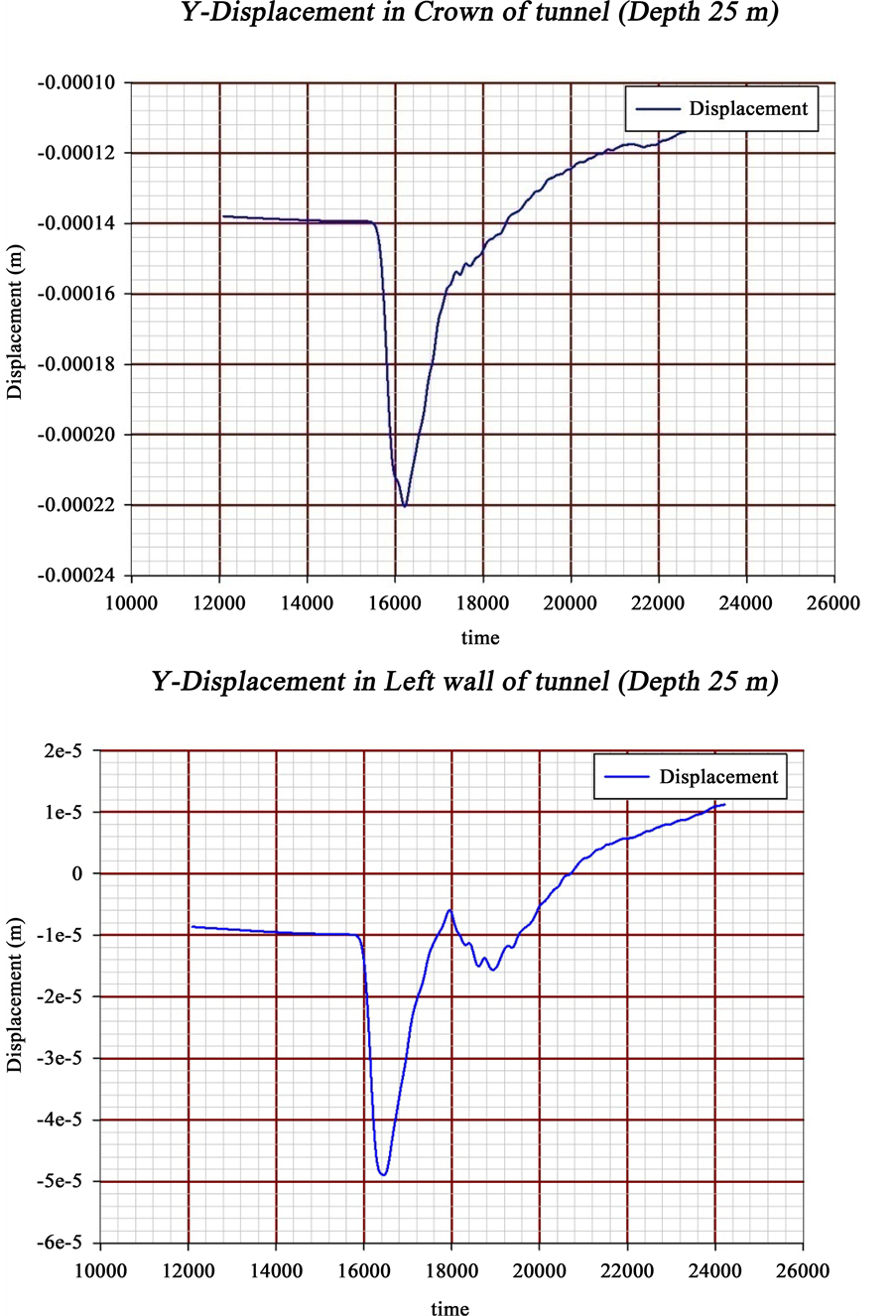
![]()
Displacement from an explosion in a tunnel (depth: 25)
![]()
Horizontal Displacement
![]()
Vertical Displacement
5. Conclusions
Results from this modeling are as following:
1) Developing is limited in depth of 15 m.
2) Minimum overload altitude is 20 m for underground structure to resist against explosion.
3) Optimal depth and stability of a tunnel is more than 25 m regarding this rock mass.
4) Studying on Tunnel Behaviors such as displacement and strain on the ceiling indicate that the tunnel will be stable if it is placed in every depth and under dynamical load equal to 10 Tons TNT but optimal depth to drill a tunnel with minimum strain is 20 - 30 m.
NOTES
![]()
*Corresponding author.